区域对流层延迟改正模型研究

孙洪飞

摘要：本文利用探空数据和CORS基站观测数据，提出了一种BP神经网络的与Hopfield模型结合，得到对流层延迟融合模型HBPF。将所建融合模型与GAMIT解算结果进行对比，证明HBPF模型是可靠的，而且是高精度的。

Abstract： In this paper， a model combining BP neural network and Hopfield is proposed to obtain the tropospheric delay fusion model HBPF by using sounding data and CORS base station observation data. By comparing the results of the fusion model with GAMIT， it shows that the HBPF model is reliable and highly accurate.

关键词：对流层延迟；Hopfield模型；BP神经网络；融合模型

Key words： troposphere delay；Hopfield model；BP neural network；fusion model

中图分类号：P228.4 文献标识码：A 文章编号：1006-4311（2017）15-0227-03

0 引言

当今社会，用户对GPS精度以及可靠性的要求越来越高，影响GPS高程精度有关的误差主要来自传播路径折射误差中的对流层折射误差。建立一个适用于多种导航定位用户精度需求的高精度对流层延迟改正模型，有着很重要的战略及现实意义[1]。

目前，国际上对流层延迟改正的方法主要是模型函数法，包括Hopfield模型、Saastamoinen模型、Black模型、UNB系列模型和EGNOS模型等。但是，由于对流层本身的复杂性，现存模型对于水汽在对流层空间的分布情况以及在时间上的变化规律仍然很难确切地描述[2]。人工神经网络模型具有学习、记忆、计算和智能处理功能[3]，在地球科学与测绘工程中发挥了重要作用。本文分析研究线性回归模型、Hopfield模型、神经网络融合模型（BP模型）、线性回归模型与神经网络融合模型（F1模型）、Hopfield模型与神经网络融合模型（HBPF模型）共五种模型对研究区域的改正效果，以期建立较高精度的区域对流层延迟改正模型。

1 Hopfield模型原理

Hopfield模型仅将大气层分为对流层和电离层两层。在对流层中，其主要分析对流层中各个气象参数与海拔高度之间的关系，然后经过推导分别得出折射率干分量和湿分量与高程之间的关系，进而后通过地面气象参数来推演整个对流层延迟。

完整的Hopfield模型的计算公式如下：

式（1）中前半部分为干延迟，后半部分为湿延迟。其中T0为测站气温，h0为测站高度，e0是地面的水汽分压，P0与T0分别为测站的地面气压与绝对温度，Hw为湿对流层顶，一般取Hw=11000m；而HT为折射率为0处的大气层高度，k1（K·mbar-1）、k2（K·mbar-1）、k3（105K2·mbar-1）为大气折射率试验常数。

Hopfield模型干延迟精度为2cm，湿延迟为5cm，另外地区和季节性变化会对模型产生3cm以上的延遲变化。欧吉坤[4]指出，在我国Hopfield模型的误差有时可达10cm以上，而且存在系统误差。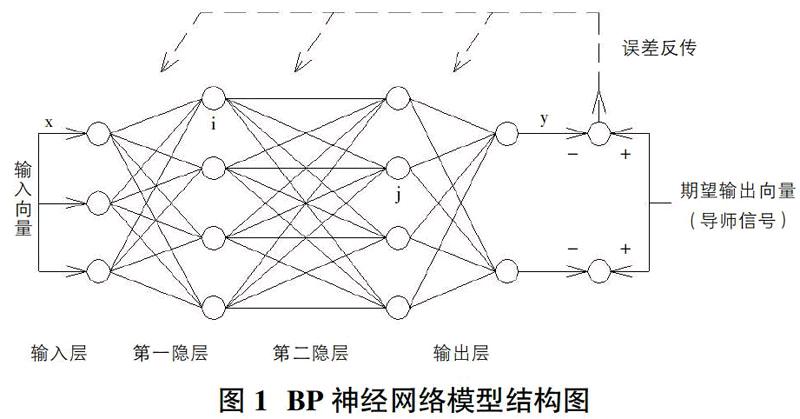

2 用于计算对流层延迟BP神经网络模型的建立

影响对流层湿延迟的水汽是一个有着极复杂变化的非线性的物理量，那么利用在处理非线性问题上有独特优势的神经网络技术来讨论延迟的变化，应该比传统的方法更有效。

在众多神经网络模型中，BP神经网络是目前应用最广泛的模型[5]。BP神经网络的模型结构包括输入层、隐含层和输出层三个部分（见图1）。

BP算法计算过程分为两个阶段：信号正向传播以及误差反向传播。这个过程引导各层权值调整，即网络学习训练的过程，这两个阶段的反复运用，在误差达到所希望的精度时，网络的学习过程就结束。

用于计算对流层延迟BP神经网络的建立主要分两个步骤：

2.1 网络结构的确定

网络结构的确定是BP神经网络在工程中应用的重要工作。需要我们确定的内容有：①输入层节点个数；为与Hopfield模型进行比较，文章采用和Hopfield模型一样的输入参数，即：测站的地面气压与绝对温度P0与T0、测站海拔高度h0以及测站的地面水汽分压e0。②输出层节点个数；输出层节点数为1，为对流层延迟δ。③隐含层节点数的选取；本文采取遗传算法和神经网络相结合的方法，将隐含层节点设置为从10～30，每次计算均输出最佳计算结果。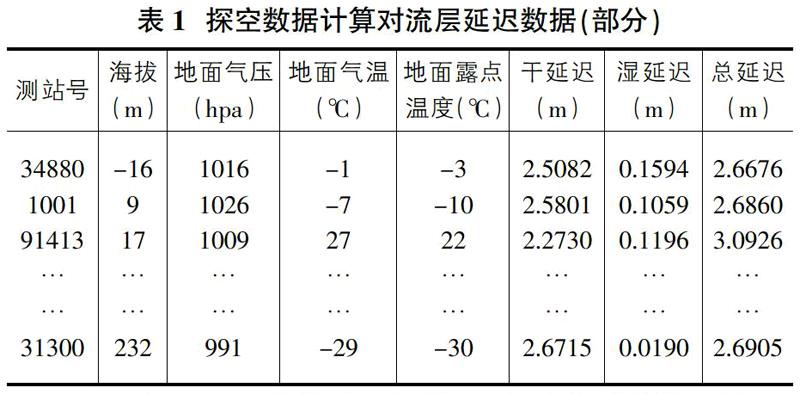

2.2 网络参数的设置

BP神经网络模型的网络参数包括：学习速率η、平滑因子α、学习误差E。通过试算，学习速率η取值范围为[0.5，2.5]，平滑因子α取值范围为[0.5，0.9]，学习误差控制E在[0.005，0.01]。

通过以上两个步骤，即建立用于计算对流层延迟的神经网络模型。

3 对流层天顶延迟的融合模型的建立

考虑到模型的应用简便特性和获取数据的限制，在此，选择Hopfield模型来与BP神经网络进行融合来建立区域对流层延迟融合模型（HBPF模型）。BP神经网络具有强大的误差补偿能力，可用来补偿Hopfield模型的系统误差，然后将所得出的误差返加到Hopfield模型上，即可求得精确的对流层延迟值。为了与HBPF模型进行对比验证，同时用BP神经网络对多元线性回归模型进行误差补偿，所得到的融合模型简称为F1模型。两融合模型具体的网型结构如下：

将地面测站的气压P0、绝对温度T0、海拔高度h0、地面露点温度td，另加Hopfield模型或多元线性回归模型计算的对流层延迟δH作为输入层，将Hopfield模型或多元线性回归模型计算延迟的误差ΔδH作为输出层，建立一个5×N×1的神经网络模型（N为隐含层节点数）。那么模型所得到的值为Hopfield模型或多元线性回归模型所得值与对流层延迟真值的误差ΔδH'。融合模型所求得的延迟δ2可通过δ2=δH+ΔδH'来计算。在具体的计算时，采用与BP神经网络相同的计算步骤。

经过上述过程，我们就建立了与BP神经网络相融合的融合模型。

4 工程及实例分析

为精确确定测站的气象参数，本文采用气象站的探空气球采集的实时大气参数作为计算数据，计算各个等压面的大气干、湿折射率，描述出测站上空对流层的折射率变化情况，再通过路径积分精确的求出探空数据在海拔高程范围内的对流层延迟值。

本文所选取的探空数据为徐州地区2010年全年的气象数据，限于篇幅问题，这里仅仅将由2010年7月1号8点的探空数据计算的部分数据列于表1。

由于气象探空数据的真实性，再加上探空数据最高高度之上所采用的中纬度大气模型与大气的真实轮廓近似，即气象探空数据高度之上延迟的无差异性，我们可以认为通过路径积分计算出来的对流层延迟与其真值无异。

4.1 对流层天顶延迟的多元线性回归模型算例

根据探空气球数据的格式，本文中的多元线性回归中自变量X将包括四个参数，分别为测站的地面气压与绝对温度P0与T0、测站海拔高度h0以及测站地面露点温度td，分别表示为X1、X2、X3、X4，待求参数就有5个，分别是a0、a1、a2、a3、a4，具体公式表达见式（2）：

然后通过最小二乘法求解出参数，得出对流层延迟与大气参数之间的多元线性关系。以表1中的数据作为学习样本，经计算得到的模型参数值如表2。

4.2 各模型检验精度汇总

为了各模型间的对比分析，每个模型均选取2010年7月1日8点的20个探空站观测数据作为学习样本，以探空数据计算得到的对流层延迟值作为基准，分别选取当天8点剩余对流层延迟样本和20点对流层延迟样本来进行检验，进而比较检验样本的精度。检验样本的精度汇总见表3。

从表3中，我们可以看出，Hopfield模型在研究区域内精度最差，线性回归模型和常规BP神经网络模型、F1模型的精度都比Hopfield模型要高，HBPF模型精度最高。这是因为，线性回归模型和常规BP神经网络模型都是对获取的四个气象参数的数学分析，没有实际的物理意义。而Hopfield模型是基于全球气象参数建立的经验物理模型，是对全球对流层延迟的模拟，在针对特定的区域应用时，会出现相应的系统误差。由于BP神经网络强大的误差补偿能力，在Hopfield模型较大系统误差下，HBPF模型能够达到最优的精度，相比其他模型，极大地提高了对流层延迟的精度。

4.3 模型计算对流层延迟精度验证

由于GAMIT软件的对流层天顶延迟参数估计精度好于±1cm[6]，因此在应用中比较公认的看法是可将GAMIT软件计算出来的对流层延迟值视为真值。本文上述融合模型是建立在探空数据的基础上的，为了进一步验证HBPF模型的有效性，将其计算结果与GAMIT计算的“真值”进行对比分析。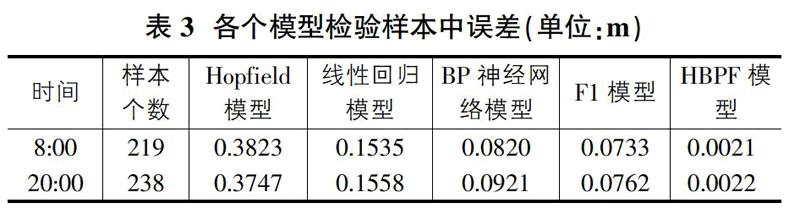

利用GAMIT软件对徐州地区5个CORS基站2010年7月份的数据进行了高精度基线解算，并得到了时间步长为2小时的对流层延迟。采用融合模型同样的计算结构，在计算CORS基站天顶对流层延迟时，学习样本依然是探空站地面气象数据（见表1）。为了进一步分析融合模型方法计算得到对流层延迟的可靠性，本文选取2010年7月25日到7月29日连续五天的数据，每天选取两个时刻（8点，20点），以GAMIT计算得到的对流层天顶延迟数据作为对比样本，并与现今常用的UNB3m模型相比。三种模型解求的某个CORS基站天顶对流层延迟值对比列表如表4。

将表4中数据绘制成图，模型数据图见图2。从图2可以看出，本文中求出的融合模型与GAMIT解算出来的结果在7月25日到7月29日期间具有相同的变化规律，两者之间的差值都在1cm左右。UNB3m模型由于是采用的差值格网模型，在选定经纬度和年积日之后，计算结果在相当长的一段时间内大致相同。

综合这几种常规模型，可以得出结论：本文得出的HBPF模型具有最高的精度，而且结果稳定可信，能够满足较高精度的GPS定位等需求。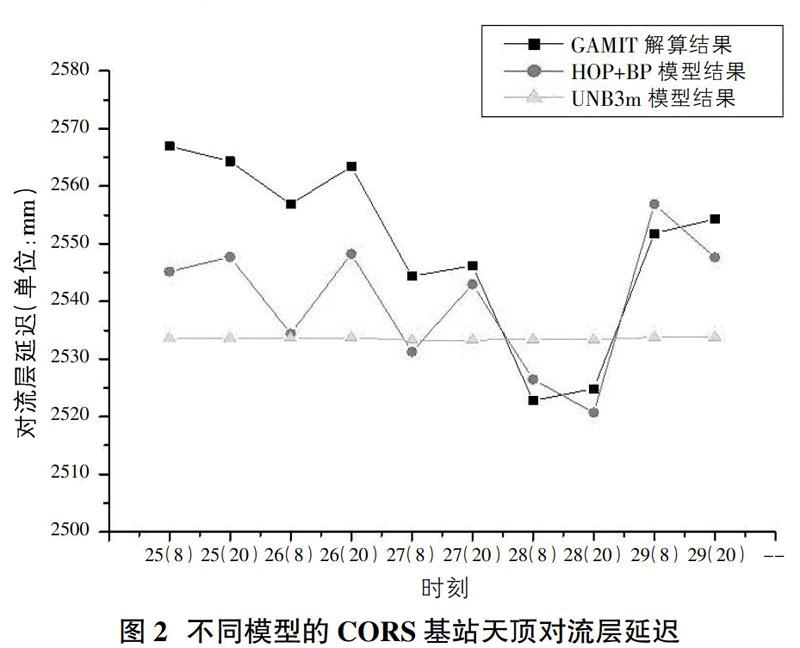

5 结束语

近年来，GPS技术已经应用到人们生活的许多方面，要提高GPS定位精度，必须要建立一个高效、可靠的对流层延迟模型来实现对对流层延迟的反演。本文利用区域实测的气象探空数据求得具有较高精度的区域融合模型HBPF模型，经验证表明其在反演区域对流层延迟方面，相对于传统模型有着更加良好的效果。但本文所选取的探空数据仅局限在徐州地区，所提出的“HBPF模型”在本区域内能取得很高的改正效果，能否在其他地区进行推广应用，也还有待于进一步验证分析。

参考文献：

[1]徐愛功，徐宗秋，隋心.精密单点定位中卫星星历对天顶对流层延迟估计的影响[J].测绘科学，2013，38（02）：19-21.

[2]戴吾蛟，陈招华，匡翠林等.区域精密对流层延迟建模[J].武汉大学学报（信息科学版），2011，36（04）：392-396.

[3]胡伍生.神经网络理论及其工程应用[M].测绘出版社，2006.

[4]欧吉坤.GPS测量的中性大气折射改正的研究[J].测绘学报，1998，27（01）：34-39.

[5]吴建生.基于遗传算法的BP神经网络气象预报建模[D]：[硕士学位论文].桂林：广西师范大学，2004.

[6]殷海涛.基于参考站网络的区域对流层4D建模理论、方法及应用研究[D].成都：西南交通大学，2006.