利用SPSS数学建模在大学生创业活动中的应用实例
2017-05-11贺靖
贺靖
摘要:简要说明如何使用统计软件SPSS的分析功能,为分析校园快递工作室的派件利润与派件营业额、宣传和日常管理费、通讯费等之间的关系,以利用SPSS19.0软件进行多元回归分析,建立派件利润与其他影响因素的回归模型,说明SPSS在解决数学建模中预测大学生创业活动遇到的经营问题时更具优越性。
Abstract: This paper briefly describes how to use the statistical software SPSS analysis function to analyze the relationship between the profit of campus express studio and the payment of the turnover, publicity and daily management fees, communication costs, etc. to use SPSS19.0 software for multivariate regression analysis, and establish the regression model of the turnover profit and other influencing factors. It shows that SPSS is more superior in solving the operational problems encountered in predicting the entrepreneurial activities of college students in mathematical modeling.
关键词:SPSS19.0;数学建模;多元回归分析
Key words: SPSS19.0;mathematical modeling;multiple regression analysis
中图分类号:G633.6 文献标识码:A 文章编号:1006-4311(2017)15-0202-03
0 引言
在数学建模中通常采用回归分析的方法建立模型来分析现实数据。回归分析是通过规定两种或两种以上变量由此来确定变量之间的因果关系或定量关系,以此建立回归模型,然后根据模型参数来评价该模型的拟合情况,并可根据自变量作进一步预测的统计方法。对比MATLAB等数学软件中较复杂的回归分析功能,SPSS突出特点是操作简便,除了录入数据和需利用键盘输入少数命令程序外,大多数操作可通过鼠标完成。而且SPSS输出结果可读性很强,只需简单的统计知识就能了解分析结果。现在SPSS提供多种统计分析方法,如统计描述、主成分分析、相关分析、方差分析以及Logistic回归等,对利用SPSS进行数学建模有很大帮助。
下面,以广州大学市政技术学院校园快递工作室的经营为例,利用SPSS19.0软件进行多元回归分析,以建立派件利润与其它影响因素的回归模型,说明其在预测现实问题时更简便和优越。
1 数据来源
学院校园快递工作室为了更好地服务师生、扩大利润、有效地控制成本的基礎上,以及运用所学知识找出派件利润与派件营业额、宣传和日常管理费、通讯费等之间的关系,从而预测出在不同因素影响下的的派件利润。为此快递工作室人员收集了过去41周工作室的派件利润与派件营业额、宣传和日常管理费、通讯费等数据。
2 数据分析
将通讯费、派件营业额、宣传和日常管理费作为自变量,派件利润作为因变量,采用SPSS19.0软件进行数据分析。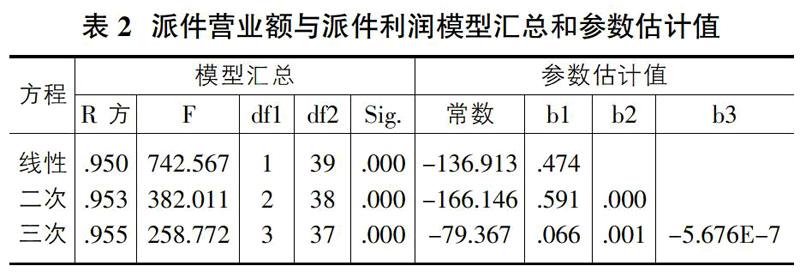
2.1 绘制散点图
首先将数据文件窗口的对话框打开,其次在菜单中栏依次点击“图形”,“旧对话框”,“散点/点状”,然后选择“简单分布”,并分别将派件营业额、宣传和日常管理费、通讯费作为自变量选入x轴,派件利润作为因变量选入y轴,绘制散点图。(图1-图3)
2.2 曲线估计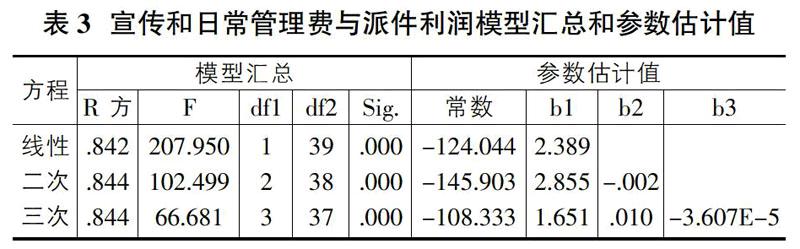
从图1-图3来看,派件营业额与派件利润以及通讯费与派件利润线性趋势较明显,而宣传和日常管理费与派件利润为曲线趋势,进行曲线估计则会判定出两个变量更合适的模型。在菜单栏依次点击“分析”,“回归”,“曲线估计”,分别将派件营业额、通讯费、宣传和日常管理费选入自变量,派件利润选入因变量,而后模型选择“线性”、“二次项”和“立方”三种曲线回归模型。
由表1可以得出,三个模型的拟合度相差不大,而拟合度最好的是三次曲线模型,其次是线性和二次曲线模型,但三方曲线模型的参数比另外两种模型的参数更多更复杂。从F值来看,线性模型F值为169.979,说明其拟合的最为显著。因此,选择线性模型最为理想,即y=β0+β1x1+ε,其中x1为通讯费,y为派件利润,ε为随机误差,βi为回归系数。线性方程为y=-145.058+1.328x1+ε。
由表2可以看出,三个模型的拟合度相差不大,其中三次曲线模型的拟合度最好,其次是线性和二次曲线模型,但三次曲线的参数比他们的参数更为复杂。从F值分析来看,线性模型F值为742.567,说明其拟合的最为显著。所以选择线性模型最为理想,y=-136.913+0.474x2+ε,其中x2为派件营业额,y为派件利润,ε为随机误差。
由表3可以得出,三个模型的拟合度也相差不大,其中二次和三次曲线模型的拟合度最好,其次是线性模型,但三次曲线模型中的参数较为复杂。从F值来看,线性模型F值为207.950,说明其拟合的最为显著。但根据以上结果还不足以选定模型,这就需要采用显著性检验方法来检测各模型的系数。重复一次上述操作,然后在曲线估计对话框中选择“显示ANOVE表格”。
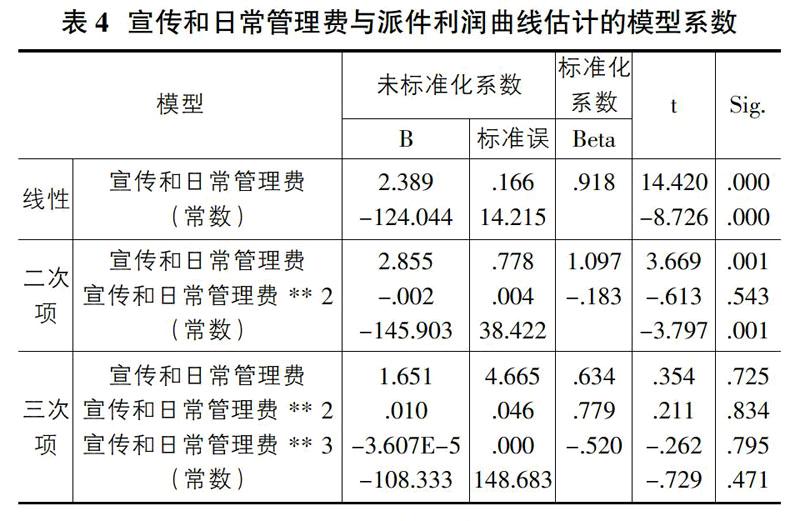
由表4可以得出,经过显著性检验后的以上模型系数,线性模型的系数通过检验均达到显著水平,而另外两种模型变量被剔除方程,因为其系数p值至少有一个大于0.05。所以线性模型最为理想,y=-124.044+2.389x3+ε,其中x3为宣传和日常管理费,y为派件利润,ε为随机误差。
3 模型建立与求解
3.1 模型一
由曲线估计知,通讯费、派件营业额、宣传和日常管理费适合线性模型,从而采用多元线性回归分析,建立通讯费、派件营业额、宣传和日常管理费与派件利润的回归模型一,y=β0+β1x1+β2x2+β3x3+ε,其中x1為通讯费,x2派件营业额,x3宣传和日常管理费,y为派件利润,ε为随机误差,βi为回归系数。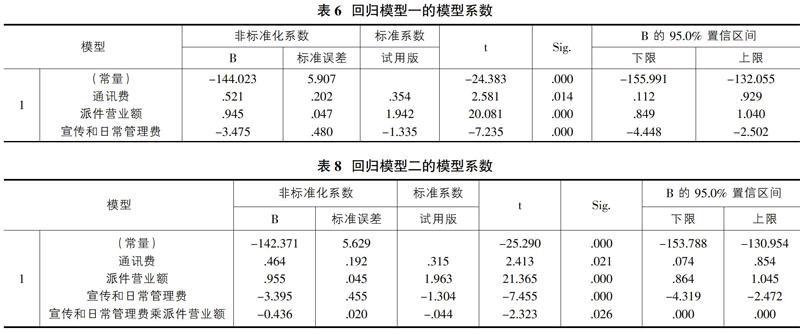
在多元回归分析时,在“分析”菜单中,先打开线性回归对话框,将通讯费、派件营业额、宣传和日常管理费同时选为自变量,再将派件利润选为因变量;点击“统计量”按钮,然后在弹出的对话框中选“置信区间”。
由表5可以得出,以通讯费、派件营业额、宣传和日常管理费共同作为自变量,模型一从分析结果来看是可取的,其联合解释98.7%的变异量,因此显著预测派件利润,
由表6可知,模型一的多元线性回归方程为y=-144.023+0.521x1+0.945x2-3.475x3+ε。其中x1为通讯费,x2为派件营业额、x3为宣传和日常管理费,y为派件利润,ε为随机误差。
3.2 模型二
虽然模型一从整体上来看较为理想,但没有考虑到多因素的交互作用,所以还需进一步修改。模型一中,派件营业额、宣传和日常管理费对于派件利润的影响是相互独立的,而且由实际情况可知,派件营业额、宣传和日常管理费之间的交互作用也可能会影响派件利润。考虑到宣传和日常管理费、派件营业额均为连续变量,所以在多元回归方程中,采用两个变量的乘积x4来代表广告费用和价格差的交互作用,记为派件营业额×宣传和日常管理费。具体操作是在多元回归分析之前,需引入新的变量。在选择“转换”菜单中,打开计算变量对话框,输入新的目标变量名,即派件营业额×宣传和日常管理费,然后在数字表达式中编辑函数,生成新的变量。然后点击线性回归对话框中,选择“绘制”这个按钮,在对话框中x轴选“*ZPRED”,y轴选“*SRESID”,再点击绘制标准化残差的散点图,而绘制标准化残差的频数分布图,则需勾选“直方图”。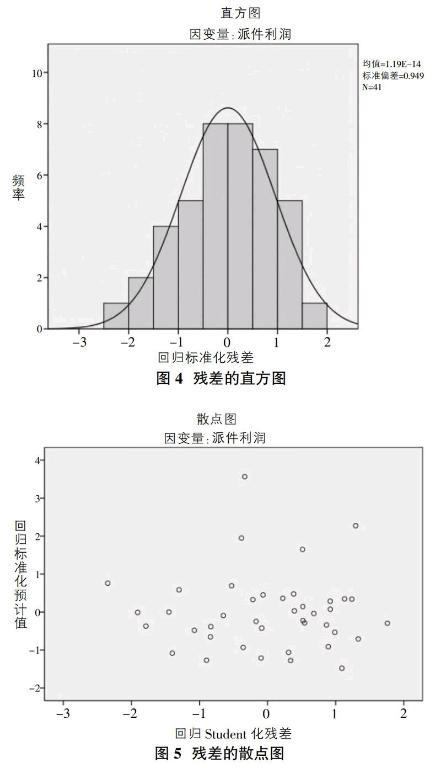
由表7和表8可知,在派件营业额×宣传和日常管理费后,联合解释98.9%的变异量,较模型一有一定提高,这说明模型二对比模型一有所改进,更贴合实际情况。模型二的回归方程为y=-142.371+0.464x1+0.955x2-3.395x3-0.436x4+ε。其中x1为通讯费,x2为派件营业额、x3为宣传和日常管理费,x4为派件营业额×宣传和日常管理费,y为派件利润,ε为随机误差。表8还显示,x4的回归系数估计值为-0.436,即派件营业额、宣传和日常管理费差存在负交互作用。因此,当派件营业额较大时,可以较少地依赖宣传和日常管理费的增加来提高派件利润;当派件营业额较小时,则需要增加宣传和日常管理费的增加来提高派件利润。
由图4可以看出,标准化残差呈现出正态分布。而图5显示,各点围绕残差为0的直线上下随机分布,因此多元回归模型对原始数据拟合情况较好。
参考文献:
[1]陈永胜,宋立新.多元线性回归建模以及SPSS软件求解[J].通化师范学院学报,2007(12).
[2]周静.在数学建模中的应用实例[J].天津职业学院联合学报,2012,(11)
[3]王兵兵.SPSS在数学建模竞赛中的应用举例——以2012年全国大学生数学建模竞赛C题为例[J].统计聚焦,2016(8).
