识别简支梁钢桥损伤的仿真分析

王冬丽+袁朝庆

摘要：简述桥梁健康监测的目的和意义，介绍了经验模态分解（EMD）的原理及波形指数的概念。为了研究桥梁结构的健康监测问题，在有限元理论基础上，运用有ANSYS软件，建立与试验室试件相对应的简支钢梁有限元模型。在模拟的时间-位移关系曲线基础上，经Hilbert-Huang变换和传统时幅域分析中的波形因数相结合，通过加瞬时激力于跨中，得到各位置处的指标值及变化率，识别了损伤位置和损伤程度。

Abstract： The purpose and significance of bridge health monitoring is described in this paper. Principle of empirical mode decomposition （EMD） and concept of shape factor are introduced. In order to study the health monitoring of bridge structure problem， based on the finite element theory， this paper uses the ANSYS software to establish the finite element model of simple supported beam steel corresponding to laboratory specimen. Based on simulated time-displacement relation curve， through the combination of Hilbert-Huang transform and the shape factor in traditional amplitude domain analysis， the parameter values and change rate of each location are got by adding instantaneous excitation force， and the damage location and damage degree are identified.

关键词：希尔伯特-黄变换；波形指数；经验模态分解

Key words： Hilbert-Huang Transform；Shape Factor；Empirical Mode Decomposition

中图分类号：U446 文献标识码：A 文章编号：1006-4311（2017）15-0134-02

0 引言

桥梁是国家的生命线工程，是国民经济发展必不可少的基础设施，桥梁结构在生产和生活中的地位和作用是举足轻重的。通过在对桥梁结构的健康监测，可以在早期发现桥梁的安全隐患，采取修护措施，有效避免造成的更大经济损失。对桥梁进行健康监测利国利民，意义重大。本文结合桥梁检测中的问题，对桥梁结构损伤识别进行仿真模拟分析。

1 EMD原理及波形因数

如今希尔伯特-黄[1]变换（Hilbert-Huang Transform，简称HHT）已被广泛应用到工程各个领域[2]。HHT的关键——模态分解法（EMD）能将信号的各种频率成分有效的以本征模态函数（Intrinsic Mode Function，IMF）的形式从时间曲线中分离出来。IMF属窄带信号，可满足Hilbert变换[3]的要求。X（t）为振动信号时间序列，

式（1）表明原始数据序列X（t）可表示为IMF分量和一个残余项之和。有研究表明[4]越早分解出来的IMF频率越高。EMD分解出的每个IMF序列都是稳态的，可以通过對其做Hilbert变换进一步分析处理。结构产生小损伤时，其物理参数的改变很小[5]，采用其物理参数识别损伤不敏感，而波形指数可很好地满足这方面要求。

2 建模及处理

模拟简支梁钢桥尺寸为576×48×5mm，钢材选择Q235。依照试验通道位置分别取关键点1、2、3、4，距离左端点依次为75mm、235mm、360mm、504mm；F为加载位置，选在跨中，激振力为30Hz正弦定频激力；裂缝位置点W，距离左端135mm。1、2、3、4、F、W均在模型上表面中线上。建模尺寸图见图1。单跨简支梁，左端节点限制ALL DOF方向位移，右端点限制UY方向位移。

模拟实验模型损伤位置，分别建立好梁、距左端135mm处1mm宽1mm深损伤梁及同位置同宽度的3mm深损伤梁，长度均为48mm。建模如图2；1处时间位移曲线为例，经验模态分解前后如图3、4。

将END分解的结果求其波形指数，将各位置处好坏参数及变化率制表。表1为好梁与1mm裂缝梁2、3阶IMF结果的波形因数比较。

由分解的数据可以找到损伤位置——W附近，将IMF3与IMF2的变化率进行比较，有明显的增大趋势，IMF3中W处的波形因数的变化率是IMF2的4.1090倍，证明更加的敏感。同样方法将梁的裂缝深度加深为3mm，然后模拟、处理、分析数据。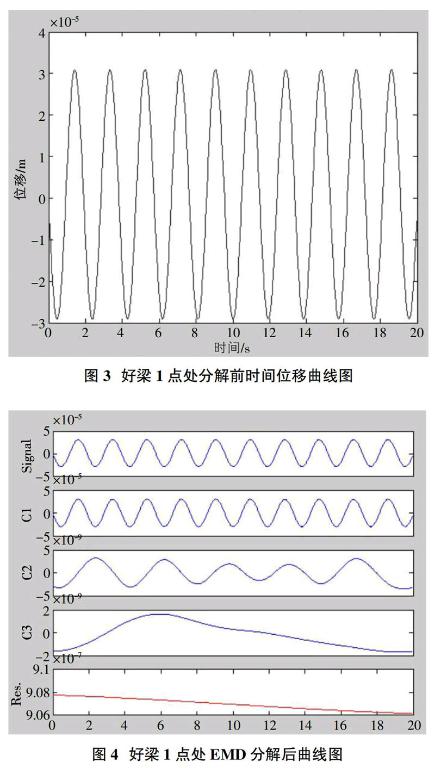

由表2可知，波形因数变化率最大处仍在W位置，再次证明能够识别损伤。以第3阶IMF中W位置处为例，3mm裂缝梁FSHA变化率为-0.6092784明显大于1mm裂缝梁FSHA变化率为-0.2524153。可以看出损伤越大参数的变化率越大。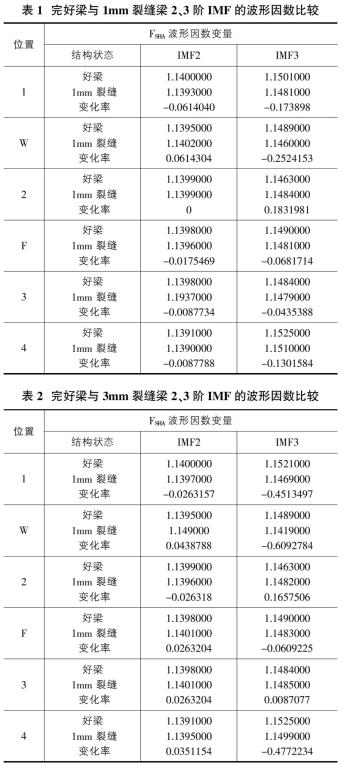

3 结论

综上所述，EMD和可以结合实现简支梁桥损伤位置的识别，经EMD分解后的数据能够提供更多的损伤信息，而且比未分解的数据效果更明显。随着裂缝深度的加大，数据显示波形因数不但可以识别损伤位置而且可以识别损伤程度。但仍然处在不足，如何对实体钢桥结构损伤识别以及HHT理论依据等问题，有待继续研究。

参考文献：

[1]Huang N E，et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis [J].Pro.R.Soc.London，1998，454： 903-906.

[2]公茂盛，谢礼立.HHT方法在地震工程中的应用之初步探讨[J].世界地震工程，2003，19（3）：39-43.

[3]胡广书.数字信号处理——理论、算法与实现.北京：清华大学出版社，1997.

[4]袁朝庆，赵丹，才英俊.基于经验模态分解法及波形指数识别简支梁桥损伤位置[J].无损检测，2007（02）：77-79.

[5]杨智春，于哲春，孙浩.一种基于经验模态分解的结构微小损伤检测方法[J].西北工业大学学报，2005，23（4）：422-425.