基于遗传算法机械手最优效率的轨迹规划研究

周建新

摘要： 随着工业机器人的发展，对工业机器人的轨迹规划研究也逐步加深。通过轨迹规划可以降低关节冲击和振动优化机器人的各种性能。在大量研究中都是以三次插值样条曲线为拟合曲线，而三次样条曲线产生的振动和冲击相对于B样条曲线较大。所以本文将通过B样条曲线拟合机器人的轨迹，再使用遗传算法全局寻优搜索时间最短的一条轨迹。

Abstract： With the development of industrial robots， the study of trajectory planning of industrial robots has been gradually deepened. Through the trajectory planning can reduce the impact of joints and vibration to optimize the performance of the robot. In a large number of studies， the cubic interpolation spline curve is used as the fitting curve， and the vibrations and shocks generated by the cubic spline curve are larger than those of the B-spline curve. Therefore， this paper will use the B-spline curve to fit the trajectory of the robot， and then use the genetic algorithm to optimize the search path for the shortest time.

关键词： 轨迹规划；B样条曲线；遗传算法

Key words： trajectory planning；B-spline curve；genetic algorithm

中图分类号：TP242.6 文献标识码：A 文章编号：1006-4311（2017）15-0104-04

0 引言

轨迹规划是研究机器人的一个重要的分支。由于这种研究是底层的基础研究不涉及高层的人工智能，扩大了研究的范围。轨迹规划就是给定一个初始点和终止点，在规划初始點至终止点的路径。我们将这种机械手空间的位置变换以数学的形式呈现。通过函数我们可以形象地知道机械手在运动过程中的各个参数以及运动的状态和位姿。在笛卡尔空间坐标中，机械手受到一系列的约束，我们可以预先给函数设置这些约束使其在空间范围内行程的轨迹在实际上是可以实现的。

如果关节运动点之间采用直线运动形成轨迹，那么在运动的过程中机械手在关节运动点会停顿，然后再开始下一段的初速度为零的运动。这种轨迹规划其中各个作业点之间的速度和加速度是不连续的会加剧机械手的冲击和振动，减少机械手的效率以及寿命。所以通过相关材料验证，三次多项式样条函数能保证工业机器人在运动中的结合点出速度和加速的是连续的，这样能是运动的轨迹是光滑的。即保证了运动平稳的要求也提高了工业机器人的工作效率。但是由于三次多项式样条曲线有局限性它只能保证各小段曲线在连接点的连续性，却无法保证整条曲线的光滑性，这就不能满足某些工程技术的要求。这样在选择样条曲线时就尽量避免选择三次多项式样条曲线。所以本文将选择使用B样条曲线提高路径的准确性。B样条曲线具有导数的连续性、分段处理性、关节位移变化率小等优点，是其在机器人的轨迹规划问题解决可以得到很好的应用。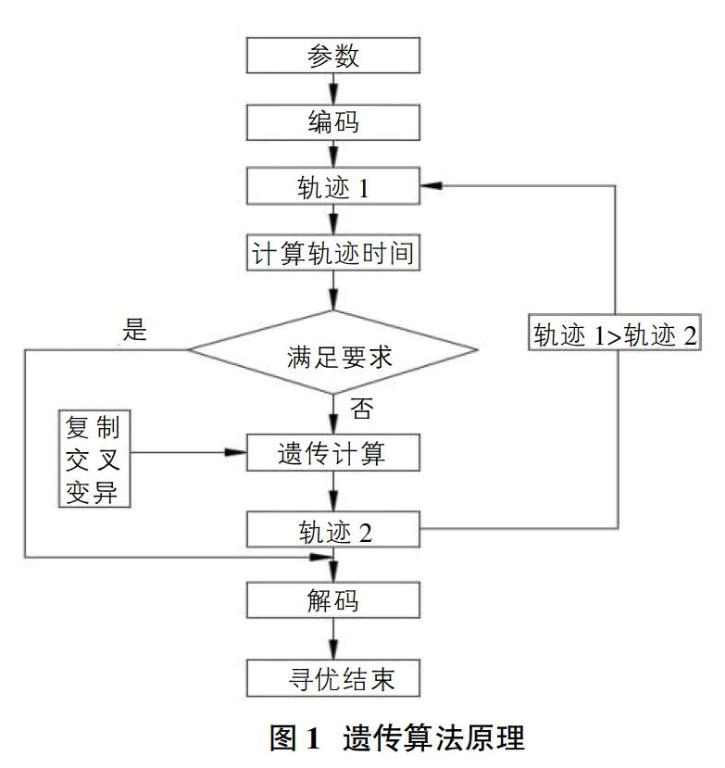

因此本文将才用B样条曲线并用遗传算法对其进行优化。在使用遗传算法的同时将以时间最优为目的，去搜索最优时间的轨迹。综上所述在数学建模中的轨迹规划定义如下：在笛卡尔空间坐标中，在已知起始点、终始点和中间点时用逆运动方程求解对应的关节坐标，在用算法计算最优的时间间隔。而实际的轨迹规划为：以数学建模中的轨迹规划为期望的运动路径，让工业机器人按照上述的路径移动。记录各个中间点处的坐标值、速度和加速度等参数实时计算其各个点的运动要素，这就是实时的轨迹跟踪。[1]

1 遗传算法的原理

遗传算法是一种模拟生物学达尔文进化论中的自然选择和遗传学机理的生物进化过程的随机化的搜索算法，将需要求解的对象模拟为自然种群，在使其种群不断进化寻其最优解的方法。遗传算法是通过生物学中的达尔文定理借鉴的，在自然的约束条件下通过筛选优等种群的规律，遗传机制通过数学模型的方式将原有求解问题转化为自然遗传变换的形式。美国的J.Holland教授在1975第一次提出通过遗传算法解决问题的方式。遗传算法的特点有可以直接对需要处理的解决问题编程，不需要通过数学建模的方式去设定一些约束；相比于通常方式能更迅速准确地搜索出最优结果；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。由于遗传算法具有这些特点，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。[2]其工作原理如图1所示。

2 遗传算法工作步骤

①对所解决工程实例的介绍。在进行解决一个实际问题使，需要就实际问题的工况条件和各种参数的约束以及要求解的目标做整体的分析，从而得出是否能用遗传算法解决问题，能否用遗传算法全局寻优找到最合适的答案。

②选取解决问题合适的编码形式和编码。编码是根据具体的问题确定出遗传算法的目的，建立合适的评价函数。通过编码可以把要解决的工程实例函数的所有参数进行数学建模，通过MATLAB仿真出遗传算法的最优解。在编码后所生成的二进制数据会形成一个染色体。每个染色体就代表遗传算法的一个解。

③初始种群。在遗传算法中随机出现的一个种群个数为N的初始种群，N是种群的大小，每个种群就代表了遗传算法可能的一个解。从一开始遗传算法就是冲初始种群出发，将待解决问题模拟成一个生物种群，逐步解决工程实例问题的过程。

④适应度的计算。其含义就是将遗传算法转换为全局寻优。遗传算法中产生的解的优劣是要有一个评价体系的，而这个评价体系就是适应度的计算。合适的适应度就是遗传算法比较优的解。但是适应度函数不是标准的，也可能随着实际问题不同的从而导致参数要求改变。

⑤选择和复制。对结果的适应度计算，从而提高了结果的可选择性这样其被复制的机会也就越来越多。在选择和复制的过程就遵循了自然界的规律“适者生存，优胜劣汰”从而选出期望的结果。

⑥交叉或基因重組。交叉运算分为两个部分，其中一个是把新复制结果和随机的两两对比，另一个是进行交叉运算。通过交叉运算将基因重组得到一个新的个体，这个个体继承了其前辈的个体特征。

⑦变异。在遗传算法的种群中随机的选择一个个体，在随机的改变这个个体中的某部分的基因，其中必须保证生成的新样本的结果是一个合理的解。变异是无序的产生新样本的过程。

⑧遗传算法终止判断。遗传算法运算过程是反复执行④-⑦步，直到满足条件，找到目标函数的最优解。1）遗传算法优化搜索到满意的最优解；2）其优化已经执行完预先定义的迭代次数；3）在预先设定的迭代数内，最优个体的适应度函数值无法改进；4）最优个体数目在群体中的比例己经达到预先设定值。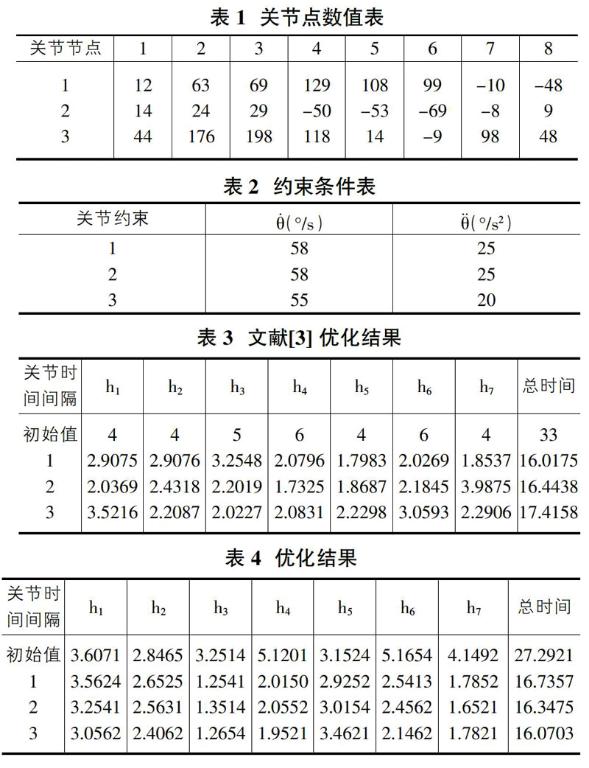

3 B样条轨迹优化数学模型

3.1 目标函数

轨迹规划数学模型中，一般以时间最短和冲击最小作为目标函数。在此将采用以时间最短为目标函数，直接对机器人的一段B样条曲线运动路径时间进行轨迹规划。

4 基于遗传算法的全局寻优

遗传算法具有分段处理的特点，每个分段都是相邻的四个控制点确定。由于B样条曲线有这样的特点，所以当B样条曲线的某个定点改变时，随之改变的只会是相邻的四段曲线，而不会改变其他的曲线。B样条曲线这个有优点对工业机器人手臂轨迹规划的体现是，工业机器人的运动路径可以分开计算，这样就可将B样条曲线的总时间也一起优化。基于时间最短的对全过程的轨迹规划，就可以分成基于时间最短对每段路径的轨迹优化。即将总时间T分为hi的分段时间。[3]

假设机器人的运动过程中会有n个中间点其中包括了起始点和终始点，这里将[t1，t2]，[t2，t3]…[tn-2，tn-1]，[tn-1，tn]规定为时间间隔序列，则每个相邻点之间的时间长度为：

hi=ti+1-tn （i=1，2，…n-1）

其中ti为工业机器人手臂运动到此中间点的时间。

使用遗传算法进行全局寻优的过程如下：

4.1 编码

把可能产生的解通过解编码成遗传算法对应的一些染色体。在本次遗传算法模拟中选取浮点编码。在对比二进制编码方式，浮点编码的一些优点如下：①浮点编码的精度跟所使用的工业机器人有关，与编码方式无关，而二进制编码会影响精度。②二进制编码的范围比较小，而且若是要扩大编码范围会以牺牲精度的代价来怎么加，而浮点编码的区域比较大。③浮点运算的遗传算子比较灵活，处理比较方便简洁。编码后的基因就排列组合形成遗传算法的染色体。

4.2 初始种群

将种群范围设定为hi（在这个时间间隔中产生），随机的在其中产生确定数量的个体组成种群。

式中，r为[0，1]区间产生的随机数，G是算法设置中的最大迭代次数，b为形状系数，本文中取b=3。由上述讨论和研究，基于遗传算法的B样条曲线插值算法具体步骤如下：

5 机器人轨迹规划结果

同过上面对遗传算法的介绍和解决步骤的梳理，因为现有实验条件本文将以埃夫特ER20-C10工业机器人为例，编写MATLAB程序。由于埃夫特ER20-C10自由度较高本此遗传算法将对工业机器人其中三个关节进行了以最优时间为目的的轨迹规划。而本文采用对轨迹样条曲线是以B样条曲线为基础进行的时间最短优化。由机器人说明书可知其优化精度应为0.0001秒。

本次计算中机器人每个关节的轨迹是9段B样条曲线所构成的，在符合实验的工况条件下，所优化的三个关节的运动轨迹所需要的时间分为16.1025s，16.2556s以及17.6232s，相对于先前未优化时间减少了9.5621s，9.4625s，9.4412s。成功将时间降低了，而在寻优的结果看来本次采用结果要优于文献[3]中采用复合形法的优化结果。

由表1数值点1和数值点8的附加节点，是根据初始条件、边界条件得出的。其中边界条件为V1=V8=0。

通过分析计算和MATLAB运行结果得到：①在工业机器人空间中，确定其轨迹上的型值点是求解优化B样条曲线轨迹的基础，其中的型值点就是逆运动学中所求出的轨迹节点。②对最优问题的求解需要建立最优模型，通过优化模型将相邻点之间的时间间隔和角速度等参数作为优化变量。建立优化曲线找出最优点。③用遗传算法的方式对B样条曲线进行优化，需要通过MATLAB进行仿真实验，求出相应的解。

参考文献：

[1]凌家良，施荣华，王国才.工业机器人关节空间的插值轨迹规划[J].惠州学院学报，2009，3.

[2]促鹤华，付荣.基于GA的时间最优化械臂轨迹规划算法[J].措制工程，2012，19（3）.

[3]王幼民，徐蔚鸿.机械臂关节空间Bezier曲线轨迹规[J].安徽机电学院学报，2000，3.