岛礁防空兵力需求分析

马新星,滕克难,侯学隆

(海军航空工程学院,山东 烟台 264001)



岛礁防空兵力需求分析

马新星,滕克难,侯学隆

(海军航空工程学院,山东 烟台 264001)

针对岛礁防空混编作战兵力需求问题,建立了岛礁防空火力单元配置距离计算模型,以此为基础,构建了满足掩护宽度要求的单一防空火力层兵力需求模型;基于Markov链建立了火力层对单目标和多目标的拦截概率模型,构建了岛礁多火力层防空总兵力需求模型,最后给出了算例分析。

岛礁防空;防空作战;兵力需求

岛礁防空兵力需求分析是岛礁防空作战兵力部署的重要环节,是进行兵力规划的重要依据[1]。岛礁地理、自然环境、岛礁防空作战任务、防空武器性能以及岛礁面临的空袭威胁等是影响岛礁防空兵力需求的主要因素[2-3]。本文以岛礁防空采用高、中、低空,远、中、近程的防御火力配系为基本假设,研究远、中、近程地空导弹混合配置,形成混编防空作战群时的兵力需求问题。本文首先建立了岛礁防空火力单元配置距离计算模型,在此基础上研究了满足岛礁防御宽度要求的单火力层防空兵力需求模型;并基于Markov链,建立了防空火力层对单目标和多目标的拦截模型,构建了岛礁防空混编作战总兵力需求模型,并结合算例进行了分析。

1 基本假设

1)为形成高、中、低空,远、中、近程的防御火力配系,充分发挥不同防空武器系统的优势,岛礁防空采用不同型号地空导弹混合配置的形式,形成混编群[3]。

2)岛礁防空火力体系由三层火力网构成:远程火力网、中近程火力网、近程火力网,采取环形配置,形成梯次拦截火力。远程火力网由中远程地空导弹组成,火力能覆盖高、中、低空空域;中近程火力网由中近程地空导弹组成,火力可覆盖中、低空空域;近程火力网由近程防空导弹组成,火力覆盖低空空域[4]。

3)防空导弹对飞机(非隐身)类目标的有效射击距离和射击高度要大于导弹类目标,本文假设以导弹类目标为抗击对象,模型对抗击飞机类目标同样适用。此外,本文主要研究防空导弹的兵力需求模型,模型对防空高炮同样适用。

4)抗击导弹类目标时,远、中程火力单元的射击范围可覆盖整个岛礁,并形成360°掩护角;近程火力单元的射击范围无法完成整个岛礁的覆盖,为构成对整个岛礁的掩护,需配置多个火力单元,形成火力衔接。

2 单层防空兵力需求模型

2.1 射击纵深与有效航路捷径

防空火力单元要完成对保卫对象的掩护任务,必须将目标消灭在完成任务线之外,为确保杀伤目标,通常要留有一定的杀伤纵深。

设火力单元两发导弹的射击时间间隔为Δtjg,火力单元一次发射n枚导弹,则其射击纵深为

Lzs=(n-1)VtΔtjg

(1)

式中,Vt为目标在某一高度的水平飞行速度[5]。

当需要进行多次拦截时,设两次拦截间的火力转移时间为Δtzy,m为拦截次数,则射击纵深为

Lzs=m(n-1)VtΔtjg+(m-1)VtΔtzy

(2)

图1为有效航路捷径与射击纵深关系图。设防空导弹位于原点O,目标沿CA方向进入,|OC|为防空导弹的水平杀伤区远界，设为Dsy,∠SOB为最大航路角qmax,|EB|为防空导弹的最大航路捷径Pmax(给定高度下能确保对目标单发射击时,发射点O与目标航向在水平面投影的最远距离),|DA|为有效航路捷径Pyx(给定高度能确保对目标发射n发防空导弹时,发射点O到目标航向在水平面投影的距离)[6],|CA|为有效抗击来袭目标所需的最小火力杀伤纵深Lzs,则由余弦定理,可得

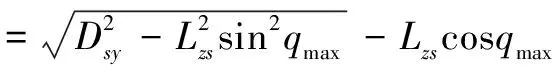
(3)

有效航路捷径为[7]

Pyx=|AD|=asinqmax

(4)

图1 有效航路捷径与射击纵深关系图

2.2 火力单元间的配置距离

防空火力单元要完成对来袭目标的有效拦截,在空间上需要一定的杀伤纵深,同时相邻火力单元间通常还要有一定的火力重叠区,以保证足够的火力密度。若相邻火力单元间距太大,则火力重叠区的杀伤纵深就小,可能导致无法对来袭目标有效拦截[8]。

图2为同型防空火力单元配置示意图,岛礁在目标来袭方向的正面宽度为L,djg ij为火力单元的配置间距,当火力杀伤纵深为Lzs时,火力单元最大配置间距为

djg max ij=Pyx i+Pyx j

(5)

式中,Pyx i、Pyx j为两个火力单元的有效航路捷径[1],可由式(4)解出。则在杀伤纵深Lzs约束条件下,两相邻火力单元在目标来袭方向所能掩护的最大宽度为djg max。

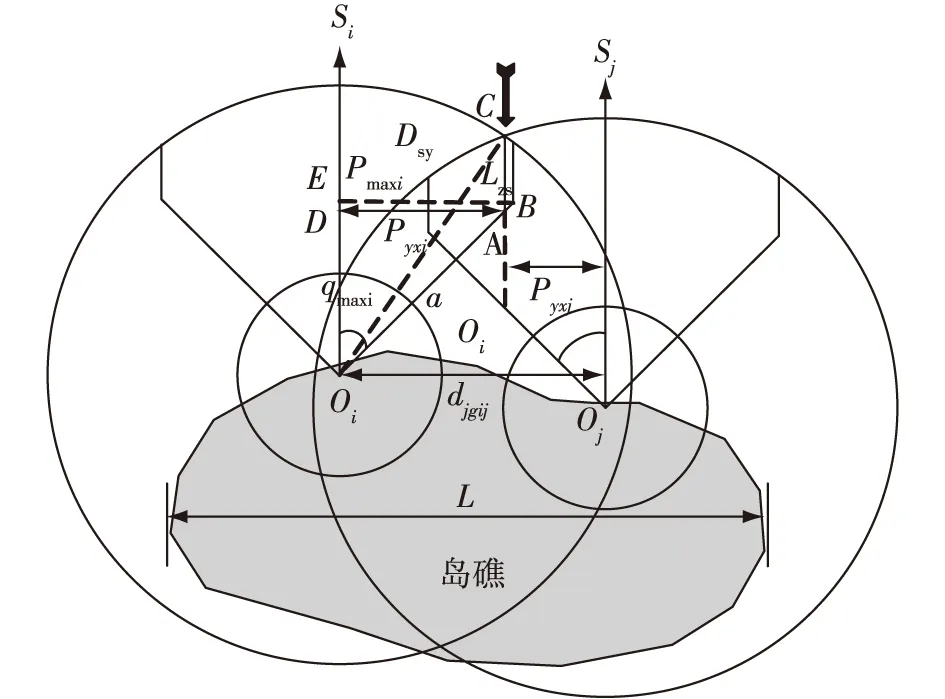
图2 同层火力单元配置示意图

2.3 掩护宽度与兵力需求

岛礁防空时,通常需对整个岛礁形成防空掩护,即所需掩护宽度为岛礁在目标来袭方向正面宽度L。当L≤djg max时,两个火力单元就可形成L的正面掩护宽度,此时两个火力单元的配置间距取为L。当L>djg max时,两个火力单元可形成的最大掩护宽度为djg max,此时需增加火力单元数,直至满足:

L≤djg max(1)+djg max(2)+…+djg max(N-1)

(6)

式中,N为火力单元总数。当然,在实际配置时,可根据兵力编制情况合理确定火力单元总数N,既保证能形成所需掩护宽度,又保证参战兵力编制的完整性。

3 多层火力拦截总兵力需求分析

单层火力需求主要针对火力层所掩护的空间范围建立需求模型,进行总兵力需求分析时,还需结合空袭强度进行分析。

3.1 单目标火力层拦截模型

单一火力层拦截一个来袭目标时,设火力层i的射击准则为si(对一个目标一波次发射si枚导弹),并设si枚导弹是以很小的时间间隔顺次与目标遭遇,其单发导弹对目标的杀伤概率为Pi,目标状态分为完好与毁伤两种,分别用1和0表示。设第d枚导弹与目标遭遇时目标的状态为x(d),x(d)∈{0,1},其中d=1,2,…,si。该随机过程为一齐次Markov链,其一步转移概率矩阵为[9]

(7)

则si步转移概率矩阵为

(8)

可解得

(9)

由式(9)可知,当一个目标经过射击准则为si的火力层后生存的概率为(1-Pi)si,其被击毁的概率为1-(1-Pi)si。

3.2 多目标单火力层拦截模型

当空袭目标为多枚导弹时,取其初始数量为m,设共有K层拦截火力层,目标群通过第k层拦截火力层后的生存数量为x(k),x(k)∈{0,1,…,m},k=1,2,…,K。则x(k)也是一随机变量,且第k+1拦截层对应的目标生存状态x(k+1)只与“现在”的x(k)相关,而与“过去”无关,所以该随机变量的变化过程也是一个Markov过程。设其第i次状态转移矩阵为

(10)

矩阵Ai中的元素Pjk表示j个空袭目标从第i拦截火力层突防,有k个目标生存的概率。式(9)中,令

(11)

(12)

3.3 总兵力需求模型

岛礁防空作战时,根据假设,分远、中、近三层火力拦截层,设来袭目标数为m,目标初始状态概率分布为a0,则a0=[1 0 0 … 0]1×(m+1),经过三层火力拦截后,目标的生存状态概率分布为

a=a0A远A中A近

(13)

式(13)中A远、A中、A近分别为远、中、近三层火力拦截层的防御矩阵,记

α=a0A远A中A近e

(14)

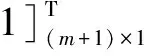
(15)

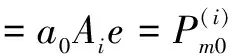
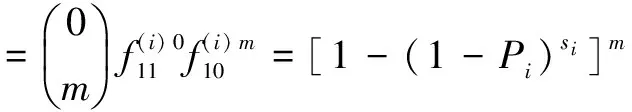
(16)

由α≥β,即[1-(1-Pi)si]m≥β,可得

(17)

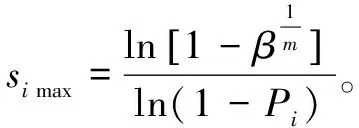
4 算例分析

本文以敌巡航导弹突击我岛礁目标为例,设敌向我发射4枚巡航导弹,两枚导弹之间的到达间隔约为25s,巡航导弹的马赫数约为0.9,飞行高度200m,不考虑电磁干扰。导弹飞行速度Vt约为300m/s。

我岛礁防空火力层中,远程火力层一套火力单元配备4枚防空导弹,中程火力层一套配备8枚防空导弹,近程火力层一套配备4枚导弹。最大可部署远程防空火力单元3个,中程防空火力单元6个,近程防空火力单元9个。各层防空导弹每枚成本分别为90万、70万、50万,对来袭目标的杀伤概率分别为0.7、0.6、0.4。我岛礁的最大正面宽度L为18km,防御效用指标β为0.95。

因近程防空导弹的射击范围无法覆盖整个岛礁,需考虑近程防空导弹满足岛礁掩护宽度要求的兵力配置需求。设我近程防空导弹对敌巡航导弹的水平杀伤区远界Dsy约为4.8km,最大航路角qmax为60°。对巡航导弹采用两发齐射,两发导弹发射间隔时间为3s。

兵力需求分析过程如下:

1)根据掩护宽度需求计算出近程防空导弹满足掩护要求的最小火力单元需求:由式(2)计算得到近程防空导弹的射击纵深Lzs为0.9km,根据式(4)、(5)分别计算出近程防空导弹的有效航路捷径Pyx为3.7km,两个火力单元最大配置间隔djg max为7.4km,根据防御最大正面宽度18km的要求,由式(6)可计算出近层防空导弹火力单元最小需求数为3。

2)由式(17)分别计算出各火力层防空导弹的最大射击准则s远max=4、s中max=5、s近max=9。

3)根据式(15),从所有可能的射击准则组合中,选出满足防御效用指标β的有效组合。

表1 有效射击准则组合

在实际选择时,一方面需要结合岛礁防空的特点,即岛礁所能容纳的防空兵力有限,装备保障困难(备弹数多的导弹优先);另一方面要考虑采用尽远拦截,梯次拦截的原则(拦截范围大的导弹优先,且三型导弹都参与拦截)。综合考虑上述因素,第16项和第17项射击准则组合比较符合要求,也可以选作射击准则。

5 结束语

本文对岛礁防空混编作战的兵力需求问题进行了研究,建立了兵力需求模型,可为岛礁防空作战指挥员决策提供参考。文中没有考虑电磁干扰对兵力需求的影响,而现代空袭与反空袭作战中电子对抗已成为常态,并扮演着重要角色,因此,在今后的研究中要进一步考虑电子对抗对兵力需求的影响,使得兵力需求模型更接近于实战条件。

[1] 徐建志, 金钊, 邓可. 舰空导弹网络化防空反导及一体化火控发展[J]. 飞航导弹, 2014(8): 46-50.

[2] 阳林, 刘付显, 张搏. 基于理想点法的区域防空部署优化方法[J]. 空军工程大学学报(自然科学版), 2014, 15(2): 49-52.

[3] 侯沛科, 周涛, 苏晨, 等. 信息化条件下防空作战兵力需求分析[J]. 兵工自动化, 2007, 26(5): 18-19.

[4] 阳林, 刘付显, 张搏. 基于风险决策的区域防空部署方案优选方法[J]. 空军工程大学学报(自然科学版), 2013, 14(6): 34-37.

[5] 王洁, 娄寿春, 王颖龙, 等. 防空导弹混合部署火力单元间配置距离的量化[J]. 系统工程与电子技术, 2006, 28(2): 263-265.

[6] 马拴柱, 刘飞. 地空导弹射击学[M]. 西安：西北工业大学出版社, 2012.

[7] 刘健. 地空导弹营离保卫目标配置距离确定方法[J]. 弹箭与制导学报, 2006, 26(2): 1196-1197.

[8] 刘健. 地空导弹火力单元配置间距计算方法[J]. 弹箭与制导学报, 2007, 27(1): 393-395.

[9] 宁伟华, 李海龙, 田新华, 等. 基于马尔柯夫链的地面防空兵兵力需求分析[J]. 电光与控制, 2006, 13(2): 57-60.

Troops Demand Analysis of Reef Air Defense

MA Xin-xing, TENG Ke-nan, HOU Xue-long

(Naval Aeronautical and Astronautical University, Yantai 264001, China)

Reef air defense troops demand with composite groups of three defense tiers is studied. Firstly, the deployment distance model of fire units is established. Based on the model, troops demand model which takes into account the cover width of one defense tier is built. Then, one tier probability model for interception of single and multiple targets is established on the basis of Markov chain. Finally, three composite tiers’ troops demand model is given on previous one tier probability model. One case analysis is presented to demonstrate the use of the models.

reef air defense; air defense operation; troops demand

2017-02-16

2017-02-27

马新星(1983-),男,江苏如皋人,博士研究生,工程师,研究方向为精确制导及作战仿真。 滕克难(1962-),男,博士,教授。 侯学隆(1979-),男,博士研究生,讲师。

1673-3819(2017)02-0001-04

TJ762.1+3；E917

A

10.3969/j.issn.1673-3819.2017.02.001