正连续函数的一个极限性质
2017-05-10樊守芳
绥化学院学报 2017年5期
樊守芳
(绥化学院信息工程学院 黑龙江绥化 152061)
正连续函数的一个极限性质
樊守芳
(绥化学院信息工程学院 黑龙江绥化 152061)
利用函数极限定义,研究了正连续函数f(x)的是常数)极限间的关系,得出了一系列结论。
正连续函数;极限;最大值;最小值

证明(1)的证明
(i)当P=0,0≤l≤+∝时,显然成立
对上述S及P>0,存在n0∈N*,使,(注:表示小于或等于x的最大整数)如果l=0,则只考虑的上界。如果l>0,则ε<l取,按照这样的理解反复使用不等式,对x≥S且x>n0、P>0时,有

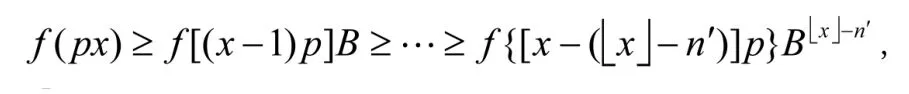
设函数f(x)在[n'P,(1+n')p]上最小值为ms'且ms'>0,则所以对x>0,有

综合(i)(ii)(iii)讨论知结论(1)成立。
(2)的证明


综上讨论知结论(2)成立。


当x取正整数n,P=1时,可得出文[1]中的结论:
推论2 设数列{un}是正项数列,若,则,其中0≤l≤+∞。
[1]GFloy.拓扑与分析习题和解答[M].周性伟,白继祖,译.北京:高等教育出版社,1985.
[2]伍胜健.数学分析[M].北京:北京大学出版社,2016.
[责任编辑 郑丽娟]
O172
A
2095-0438(2017)05-0156-02
2016-12-06
樊守芳(1965-),男,黑龙江肇东人,绥化学院信息工程学院副教授,硕士,研究方向:基础数学及函数论。
