利用计算全息光栅产生的涡旋光测量物体变形

史凯, 张新宇, 孙平

(山东师范大学物理与电子科学学院 , 山东 济南 250014)

【光纤与光子传感技术】

利用计算全息光栅产生的涡旋光测量物体变形

史凯, 张新宇, 孙平*

(山东师范大学物理与电子科学学院 , 山东 济南 250014)

利用计算全息(CGH)光栅产生的涡旋光束拉盖尔-高斯(LG)光束进行离面位移测量。基于二元叉形光栅产生LG光束的理论，将产生的LG光束作为参考光，加入一束平面光作为物光，设计了离面变形测量实验方案。利用物光和参考光的干涉进行物体变形测量，推导出物体变形前和变形后的干涉光强公式。通过数值计算，分析了利用LG光束进行变形测量的原理。数值模拟实验结果与理论结果基本一致，表明利用CGH叉形光栅产生的高纯度的LG光束可以进行物体变形测量。

拉盖尔-高斯光束；变形测量；干涉；相移

涡旋光是具有螺旋型相位波前和相位奇点的光束，因含有相位因子exp(ilφ)，相位奇点处光波的光强为0，呈现为中心为暗核的光圆环，相位围绕奇点沿垂直于传播方向呈螺旋状分布[1]，在传播过程中波前会绕着传播方向以螺旋的方式前进[2]。涡旋光具有轨道角动量(orbital angular momentum,OAM)，在光学镊子[3]、光学扳手[4]、量子通信[5]及生物医学等领域具有很高的应用价值，引起人们的广泛关注和研究。

近几年来，利用涡旋光测量物体微变形已经开展了许多研究。光学涡旋干涉仪(optical vortex interferometer，OVI)利用三束平面光进行干涉，形成可以精确定位的涡旋点阵，对变形前后的涡旋点阵的位置变化进行记录分析，从而对物体的微小变形进行精密测量[6]。光学涡旋计量术(optical vortex metrology，OVM)利用希尔伯特滤波产生的随机分布的白光散斑图样，及其复解析信号的伪相位信息中的相位奇异性进行精密测量[7-8]。将传统的电子散斑干涉技术与液晶空间光调制器(liquid crystal spatial light modulator，LCSLM)相结合，能够测量物体的微小形变[1-2]。将光学涡旋点阵与电子散斑技术相结合，基于涡旋光的干涉特性可以测量物体离面位移。利用OVI进行测量时，涡旋点阵定位精准，光路简单，但涡旋点阵的利用率低，计算的精准度不够。虽然利用OVM进行变形测量时不需要借助于干涉，但是其计算过程过于复杂。

拉盖尔-高斯(Laguerre Gaussian,LG)光束是一种典型的涡旋光束[9]，LG光束的波前具有连续的螺旋相位、中心光强为0，绕相位奇点旋转一周相位变化2lπ(l为拓扑荷数)，且具有确定的OAM[10]。因此，可以利用LG光束作为物光或者参考光测量物体的形变。为了精确测量物体形变，首先必须要产生高纯度的LG光束，可以采用柱面镜系统光束变换法[11]、计算全息(computer-generated hologram，CGH)光栅法[12-13]等。柱面镜系统光束变换法虽然可以产生较高质量的LG光束，但其对装置的调整要求非常高。CGH具有灵活、快速和计算机实时可控等优点，应用比较广泛，但这种方法对全息图的精确度要求严格，光路比较复杂，衍射效率较低，无法抑制不需要的衍射级。而空间光调制器(spatial light modulator,SLM)可以对光波进行空间分布调制，将利用计算机模拟设计的CGH光栅直接显示到纯相位SLM上即可产生LG光束，其光路简单，拓扑荷数可控，可以产生高质量的涡旋光。

本文利用LG光束测量物体的离面位移。将CGH光栅输入到液晶空间光调制器上，用LG光束照射，经过SLM的调制，在一定衍射距离的特定级数上产生LG光束，并将其作为参考光；在光路中引入另一束平面光作为物光，两束光干涉形成分叉的干涉条纹。模拟了物体变形前和变形后形成的干涉图样，运用四步相移的方法模拟计算出变形相位，通过对变形相位解包裹，比较物体离面变形相位的理论变形相位的三维图像，发现模拟结果和理论值相吻合，说明LG光束对于物体变形测量具有重要的应用价值。

1 原理

1.1 利用二元CGH叉形光栅产生LG光束

如图1所示，将二元CGH叉形光栅(图2)输入到LCSLM中，将准直的LG光束投射到LCSLM，通过调节LCSLM上前后两偏振片，在一定距离处通过电荷耦合元件(charge-coupled device，CCD)捕捉到衍射图样。则透过光栅后的出射光的远场分布[10]为：

图1 利用二元CGH光栅产生LG光束的光路图Fig.1 Optical path to produce LG beam using the CGH grating

图2 二元CGH叉形光栅Fig.2 CGH grating

(1)

其中，l为拓扑荷数，θ为平面波与z轴的夹角，νx为空间频域的直角坐标分量，(ρ1，f1)是远场的空间坐标(空间角频域极坐标)。由式(1)可知，高斯基模经过CGH光栅后，形成的远场分布可以看成是所有级次的衍射光的叠加，基于光的干涉、衍射和全息成像原理[14]，将一束LG光束照射到LCSLM上的二元CGH叉形光栅，经SLM调制后，在光栅后的衍射屏上会呈现一系列的衍射光，在某一特定级次上即为LG光束，即除去中央零级是LG光束外，其他级次都为LG光束，但超过±2级的LG光束光强相对较弱。

图3所示为LG光束照射拓扑荷分别为l=1(图3a)和l=2(图3b)的二元CGH叉形光栅后形成的衍射规律模拟图。

图3 LG光束照射CGH光栅后形成的衍射图样Fig.3 Diffraction patterns formed by LG beam irradiating the CGH grating

由图3可以看出，中央零级为LG光束，在±1级、±2级……会产生较高纯度的LG光束，且随着拓扑荷数的增加，中心暗斑的半径逐渐增大。

1.2 利用产生的LG光束测量物体变形

如图4所示，激光器射出的准直激光为LG光束，经过半透半反镜BS1将激光分为两束，一束光作为物光，经过扩束镜扩束后变为平面光照射到物体表面；另一束LG光束投射到SLM上，产生LG光束并将其作为参考光，经反射镜M1反射和扩束镜扩束后，与从物体表面反射回来的物光发生干涉，通过CCD捕捉干涉图样。利用压电陶瓷(piezoelectric ceramic transducer，PZT)相移器实现移相。

图4 利用产生的LG光束测量物体变形实验光路图Fig.4 The experimental optical path using LG beam to measure the deformation of the object

将沿着z轴传播的LG光束作为参考光，其横向电场分布为:

(2)

将一束平面光作为物光：

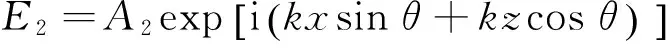
(3)

将平面光以与z轴的夹角为θ的方向与LG光束进行干涉，在z=0平面内，得到两束光干涉后的相位为：

ψ(ρ,φ,z)=lφ+kxsinθ。

(4)

被测物体没有变形时，得到干涉条纹的强度分布：

(5)

其中

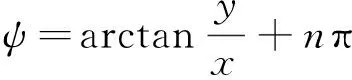
(6)

l=1,2,3,…是LG光束的拓扑荷数，ψ0是任意的相位因子，φ为方向角，为了使0≤φ≤2π，

(7)

为了便于讨论，取加载的变形相位为：

φ(x,y)=(x2+y2)×0.000 5×2π 。

(8)

当被测物体加载离面变形后，LG光束和平面光干涉条纹的强度分布：

(9)

其中，ψ(x,y)为由于物体形变引起的相位变化。

用计算机模拟变形前拓扑荷为l=1的LG光束与平面光干涉形成的干涉条纹，见图5。

图5 拓扑荷为l=1的LG光束与平面光干涉形成的干涉条纹 Fig.5 The interference fringes formed by the LG beam with the topological charge of 1 and the plane light interference

2 物体离面位移变形测量模拟

当物光为平面光，参考光为LG光束时，在物体变形之前，引入四步相移法，得到4幅光强分布图像(图6a)：

(10)

(11)

给物体加载Δψ=0.025×ψ的变形相位，同样运用四步相移，得到变形后的4幅光强分布图(图6b)：

(12)

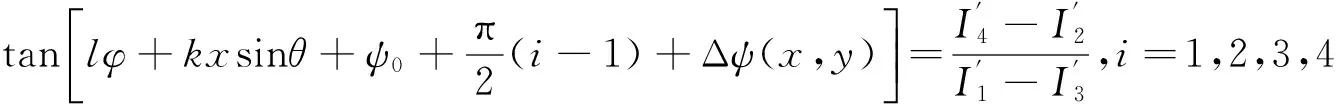
(13)

由式(11)、(13)可得出物体的变形相位为：

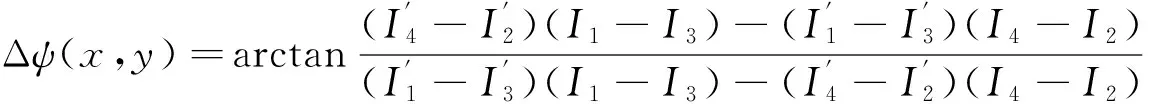
(14)

图6 运用四步相移法得到的变形前后的光强图Fig.6 The light intensity distribution charts of before and after the tested object deformed obtained by four step phase shifting method

用四步相移的方法模拟计算出变形相位，然后对变形相位解包裹，得到的三维相位图如图7a所示，理论加载的变形相位的三维图像如图7b所示。由图可以看出，实验模拟得到的变形相位与理论加载的变形相位一致，而且对于l不同的LG光束以及不同的入射角度，所得的结果基本一致。以上结果表明，可以利用二元CGH叉形光栅产生的LG光束测量物体的形变。

进行模拟时的参数设置：l=1，λ=632.8 nm，衍射距离L=31 mm，θ=60 rad。

图7 实验模拟和理论加载的三维变形相位Fig.7 The three-dimensional phase distribution of simulation and the theoretical value of out-of-plane displacement

3 结论

本文利用二元CGH叉形光栅和SLM相结合的方式，产生较高纯度的LG光束，利用高质量的LG光束与平面光干涉实现了离面位移的测量。该方法光路简单，拓扑荷可控，能够产生较高质量的涡旋光，提高了变形测量的准确性，且数值模拟实验结果与理论结果基本一致。研究结果表明，利用本文中的方法产生的LG光束可以用于物体离面位移测量，为准确测量物体变形提供了新方法。

[1]孙海滨,孙平. 涡旋光用于物体面内位移变形测量的模拟[J]. 光电子·激光, 2014，25(11):2252-2258.

[2]孙平, 李兴龙，孙海滨，等. 涡旋光的干涉特性及其在变形测量中的应用[J]. 光子学报, 2014, 43(9):130-134.

[3]GAHAGAN K T, SWARTZLANDER G A. Optical vortex trapping of particles[J]. Optics Letters, 1996,21(11):827-829.

[4]SIMPSOM N B,DHOLAKIA K,ALLEN L, et al. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner[J]. Optics Letters, 1997,22(1):52-54.

[5]MAIR A,VAZIRI A, WEIHS G, et al. Entanglement of the orbital angular momentum states of photons[EB/OL]. [2016-12-01]. http://dx.doi.org/10.1038/35085529.

[6]SENTHILKUMARAN P, MASAJADA J, SATO S. Interferometry with vortices[J/OL]. International Journal of Optics,2012(2012): 517591[2016-12-01]. http://dx.doi.org/10.1155/2012/517591.

[7]KAUFMANN G H. Advances in speckle metrology and related techniques[M].Weinheim,Germany: Wiley-VCH，2011.

[8]WANG W,ISHII N, HANSON S G, et al. Phase singularities in analytic signal of white-light speckle pattern with application to micro-displacement measurement[J]. Optics Communications, 2005, 248(1/2/3): 59-68.

[9]GALVEZ E J, CRAWFORD P R, SZTUL H I, et al. Geometric phase associated with mode transformations of optical beams bearing orbital angular momentum[J]. Physical Review Letters, 2003, 90(20): 203901.

[10]李丰, 高春清，刘义东，等. 利用振幅光栅生成拉盖尔高斯光束的实验研究[J]. 物理学报, 2008, 57(2): 860-866.

[11]PADGETT M J, ALLEN L . The angular momentum of light: Optical spanners and the rotational frequency shift[J]. Optical and Quantum Electronics, 1999，31(1): 1-12.

[12]HECKENBERG N R, MCDUFF R, SMITH C P, et al. Generation of optical phase singularities by computer-generated holograms[J]. Optics Letters, 1992，17(3):221-223.

[13]JAISWAL V K, SINGH R P, SIMON R. Producing optical vortices through forked holographic grating: Study of polarization[J]. Journal of Modern Optics, 2010, 57(20):2031-2038.

[14]LI S X, WANG Z W. Generation of optical vortex based on computer-generated holographic gratings by photolithography[J]. Applied Physics Letters, 2013, 103(14):141110.

[15]蔡长青,贺玲凤. 基于四步相移的相位差提取方法[J]. 华南理工大学学报 (自然科学版), 2011, 39(9):93-96.[16]杨福俊,耿敏，戴美玲，等. 基于单频四步相移条纹投影的不连续物体三维形貌测量[J]. 光电子·激光, 2012(8):1535-1538.

Measurement of object deformation using vortex beams generated by a computer-generated hologram grating

SHI Kai, ZHANG Xin-yu, SUN Ping*

(School of Physics and Electronics,Shandong Normal University, Jinan 250014，China)

∶The out-of-plane displacement can be measured by using a vortex beam, Laguerre Gaussian (LG) beam, produced by computer-generated hologram (CGH) grating. Based on the principle of using the computer-generated hologram (CGH) grating to produce LG beam, the experimental scheme of the out-of-plane deformation measurement was designed, using the LG beam as reference light and a plane beam as object light. The object deformation was measured by the interference of object light and reference light, and the interference beam intensity formula before and after the tested object deformed was derived. Adopting the method of numerical calculation, the principle of using LG beam for the measurement of object deformation was analyzed. The numerical simulation results were in agreement with the theoretical results, which showed that by the high purity LG beam produced by CGH grating can be used for out-of-plane displacement measurement.

∶ Laguerre Gaussian beam; deformation measurement; interference; phase shift

10.3976/j.issn.1002-4026.2017.02.010

2016-12-19

山东省科技攻关项目(2012GGB01081)

史凯(1992—)，女，硕士研究生，研究方向为图像处理。E-mail：sksdnu@163.com

*通信作者,孙平(1964—)，男，博士，教授，研究方向为光电精密检测技术。E-mail:sunpingmail@163.com

O438

A

1002-4026(2017)02-0061-06