走进南京市中考数学中的概率常见考法

孔小红

（江苏省南京市高淳区固城中学）

《义务教育数学课程标准》对概率部分的要求主要体现在两方面：一是从事件本身发生的可能性来把握概率；二是通过大量重复试验用频率来估计概率。结合实际背景，考查概率知识的有关概念以及计算简单随机事件的概率等内容仍然是南京市近年数学中考的主要形式。这种考法上的变化，对教学具有正确的导向作用。

在解决初中概率统计中等可能性的结果的有关问题时，当等可能性结果的总数量不多时，我们通常把要计数的所有对象一一直接列举出来，从而求出其总数，这种最简单、最基本的计数方法叫做直接列举法。有不少学生认为直接列举法是“最烦、最繁、最差、最没有技术含量”的方法，其实不然：第一，当基本事件总数较少但情况又稍复杂时，直接列举法一清二楚；第二，直接列举法应当是解这类题时首先想到的方法，其次是树形图、列表法等；第三，即使直接列举失败，也可由此发现部分规律，对解题亦有帮助。因此，解决计数问题时，应重视直接列舉法。

例1.（南京市2012中考题7分）甲、乙、丙、丁4名同学进行一次羽毛球单打比赛，要从中选2名同学打第一场比赛，求下列事件的概率。

（1）已确定甲打第一场，再从其余3名同学中随机选取1名，恰好选中乙同学；

（2）随机选取2名同学，其中有乙同学.

【解析】解：（1）已确定甲打第一场，再从其余3名同学中随机选取1名，恰好选中乙同学的概率是1/3.

（2）从甲、乙、丙、丁4名同学中随机选取2名同学，所有可能出现的结果有：（甲、乙）（甲、丙）（甲、丁）（乙、丙）（乙、丁）（丙、丁），共有6种，它们出现的可能性相同，所有的结果中，满足“随机选取2名同学，其中有乙同学”（记为事件A）的结果有3种，所以P（A）=二分之一。

例2.（2015江苏省南京市，22题，8分）某人的钱包内有10元钱、20元钱和50元钱的纸币各1张，从中随机取出2张纸币。

（1）求取出纸币的总额是30元的概率；

（2）求取出纸币的总额可购买一件51元的商品的概率。

【解析】解：某人从钱包内随机取出2张纸币，可能出现的结果有3种，即（10，20）、（10，50）、（20，50），并且它们出现的可能性相等。

（1）取出纸币的总数是30元（记为事件A）的结果有1种，即（10，20），所以P（A）=三分之一。

（2）取出纸币的总额可购买一件51元的商品（记为事件B）的结果有2种，即（10，50）、（20，50）。所以P（B）=三分之二。

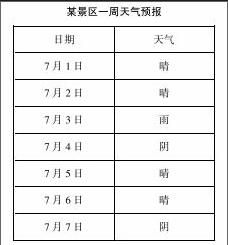
例3.（2016江苏省南京市， 8分）某景区7月1日—7月7日一周天气预报如下，小丽打算选择这期间的一天或两天去该景区旅游，求下列事件的概率：

（1）随机选择一天，恰好天气预报是晴；

（2）随机选择连续的两天，恰好天气预报都是晴。

【解析】解：（1）随机选择一天，天气预报可能出现的结果有7 种，即7 月1 日晴、7 月2 日晴、7 月3 日雨、7 月4 日阴、7 月5 日晴、7 月6 日晴、7 月7 日阴，并且它们出现的可能性相等。恰好天气预报是晴（记为事件A）的结果有4 种，即7 月1 日晴、7 月2 日晴、7 月5 日晴、7 月6 日晴，所以P（A）=七分之四。

（2）随机选择连续的两天，天气预报可能出现的结果有6 种，即（7 月1 日晴，7 月2 日晴）（7 月2 日晴，7 月3 日雨）（7 月3 日雨，7 月4 日阴）（7 月4 日阴，7 月5 日晴）（7 月5 日晴，7 月6 日晴）（7 月6 日晴，7 月7 日阴），并且它们出现的可能性相等。恰好天气预报都是晴（记为事件B）的结果有2 种，即（7月1 日晴，7 月2 日晴）、（7 月5 日晴，7 月6 日晴），所以P（B）=六分之二=三分之一。

小结：在学习等可能性条件下的概率计算和等可能性的结果计数时，不遵循数序规律，东举一个，西举一个，不按顺序列举，往往会出现遗漏或重复，有序地思考、合理地分类，才是解决这类问题最关键的思维。使用直接列举法进行计数时，要注意以下几点：（1）初步估计，总的数目不太多，又没有更简捷的办法；（2）为了使枚举的结果不重复又不遗漏，我们要抓住对象的特征，选择适当的标准分类，有次序、有规律地列举。

编辑 李建军