基于Markov链的客户剩余生命周期度量方法研究

王 锐，李 冰,刘 勤

(1.江西理工大学 经济管理学院，江西 赣州 341000；2.江西师范大学 软件学院，江西 南昌 330031；3.武汉理工大学 管理学院，湖北 武汉 430070)



基于Markov链的客户剩余生命周期度量方法研究

王 锐1，李 冰2,刘 勤3

(1.江西理工大学 经济管理学院，江西 赣州 341000；2.江西师范大学 软件学院，江西 南昌 330031；3.武汉理工大学 管理学院，湖北 武汉 430070)

客户剩余生命周期对客户价值的度量有重要的意义，但当前关于这一领域的研究较为缺乏。基于此，提出了基于马尔可夫链的客户剩余生命周期度量方法。首先，对处于生命周期各阶段客户的状态转化空间进行了分析，并在此基础上确定了生命周期各阶段客户的状态转化过程。然后，运用带单侧流失壁的马尔可夫链对客户在生命周期中的状态转化过程进行了分析。接着，运用马尔可夫链中首次通过时间的计算方法对客户剩余生命周期进行了度量。最后，以江西某电信运营商的客户数据对笔者方法的有效性进行了实证。

客户剩余生命周期；马尔可夫链；客户价值

随着互联网技术的高速发展，企业的竞争环境发生了翻天覆地的变化，企业间的竞争由以产品或服务为中心逐渐转化为以客户为中心。在此过程中，企业越来越注重客户体验，而良好的客户体验往往需要支付高昂的费用，但企业的资源是有限的，因此，企业需要对现有客户进行细分，并从中选取高价值的客户群体，为这些客户提供高品质服务以提高企业的盈利能力。而客户价值是企业进行客户细分的重要依据[1]。客户价值计算方法主要为JACKSON于1985年在传统的净现值分析思路基础上提出的CLV公式及其扩展方法[2]。在这些方法中，客户的生命周期时长是重要的参数。但在实际计算客户价值的过程中，绝大多数的研究者均是根据经验事先定出客户的生命周期时长[3-5]，这严重制约着客户价值计算的准确性。因此，如何计算客户的生命周期对客户价值的度量有着重要的意义。而在客户生命周期的计算过程中，客户剩余生命周期(即客户由当前状态到流失之前所经历的时间)的度量是其中的关键。而关于客户剩余生命周期度量的研究较少，因此开展此项研究将具有较大的理论及现实意义。

1 客户的状态转化过程

在客户生命周期阶段划分领域，DWYER等认为一个完整的客户生命周期由考察期、形成期、成长期、成熟期和衰退期5个阶段构成[6]；陈明亮等则将客户生命周期简化为考察期、形成期、稳定期及退化期4个阶段[7-10]；MA等则在文献[6]客户生命周期5阶段模型的基础之上，根据客户的流失过程的特点，将客户生命周期调整为接触期阶段、成长期阶段、成熟期阶段、潜在流失阶段、流失阶段[11]。因此笔者在上述研究的基础之上，将客户的生命周期划分为接触期、成长期、成熟期、衰退期和流失期5个阶段。生命周期各阶段客户的状态转化过程如下：①对于接触期的客户而言，客户的状态转化存在两种情形：一是客户由接触期进入成长期，二是客户由接触期直接进入流失期。②对于成长期的客户而言，客户的状态转化根据客户的忠诚度可能出现下列情形：对于忠诚度较高的客户，一是保持当前的状态不变，二是由成长期进入成熟期；对于忠诚度较低的客户，客户则可能跨越成熟期直接进入衰退期，或是客户由当前状态直接转变为流失客户。③对于成熟期的客户而言，根据客户的忠诚度，其状态转化同样存在4种可能性：一是保持当前状态不变，仍为成熟期客户；二是进入下一阶段成为衰退期客户；三是回到成长期，重新成为成长期客户；四是直接流失，成为流失客户。④对于衰退期的客户，其可能保持当前状态不变；也可能进入下一阶段成为流失客户；还可能从新回到成长期，成为成长期客户；再或是从新回到成熟期，成为成熟期客户。⑤对于流失期的客户而言，流失阶段则是客户生命周期的终点，一旦成为流失客户，则客户的生命周期也就结束了，此时客户的状态再也无法转变为其他状态。因此，生命周期各阶段客户的状态转化过程可用图1表示，其中，1～5分别表示处于接触期、成长期、成熟期、衰退期和流失期的客户。

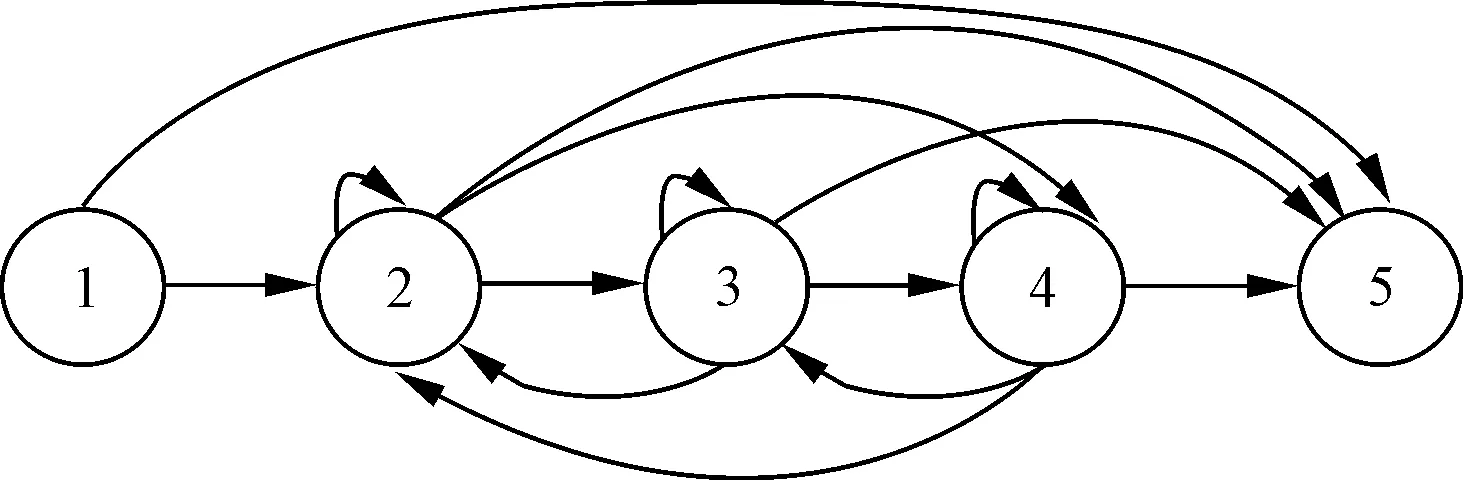
图1 生命周期各阶段客户的状态转化过程

2 客户剩余生命周期的度量

通过图1中生命周期各阶段客户的状态转化过程可发现：客户下一阶段的状态仅由客户当前的状态所决定，而与之前的状态无关，因此客户在生命周期各阶段的状态演化过程具有无后向性。另外，不管处于何种状态的客户，其一旦进入流失阶段，客户的状态就不会再发生任何变化了(即流失状态不能转变为其他状态)，因此客户的流失状态可被视为吸收态。基于此，可认为客户在生命周期各阶段的状态演化过程是一个以接触期为起点，以流失期为吸收壁的带单侧吸收壁的马尔可夫链。因此，可以采用马尔可夫链中首次通过时间的计算方法来对生命周期各阶段客户的剩余生命周期进行度量。具体过程如下：

(1)客户状态转化概率的计算。设Ni(t-1)为t-1时期处于状态i的客户人数，Nij(t-1,t)为t-1到t时期这一时间段内，由状态i转移到状态j的客户人数。则从t-1时期到t时期的客户状态转化概率矩阵可记为：Pt={pij}k×k，pij表示客户的状态由i转化为j的概率，由式(1)进行计算。

(1)

假设当前处于t时期，Pt,1,Pt,2,Pt,3,Pt,4,Pt,5分别为处于接触期、成长期、成熟期、衰退期及流失期的客户状态转化向量。对于Pt,1而言，由图1可知t时期处于接触期的客户到了t+1时期，其状态只能变为成长期客户或流失客户。所以，p11=0,p13=0,p14=0。此时，Pt,1=(0,p12,0,0,p15)；另外，由于流失期为吸收态，即客户一旦成为流失客户，客户的状态再也无法转化为任何其他状态，所以，Pt,5=(0,0,0,0,1)。同样，根据图1可得到Pt,2,Pt,3,Pt,4。因此，客户在t-1时期到t时期之间的状态转化概率矩阵Pt可用式(2)表示。

(2)

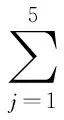
(3)

(2)客户剩余生命周期的计算。 由上述分析可知，客户在生命周期中的状态转化过程是一个由接触期为起点，成长期、成熟期和衰退期3个阶段可相互转化，流失阶段为吸收态的马尔可夫链。因此，运用马尔可夫链中首次通过时间的计算方法计算出客户的剩余生命周期[12]。

设Tij为客户状态首次由i转变为j的期望时间，已知客户的流失期为吸收态，因此T15,T25,T35,T45可分别表示接触期、成长期、成熟期和衰退期客户的剩余生命周期。对于Tij而言，其由两个部分构成：一是客户的当前状态为i，而在下一个时期其状态就转变为j，此时，客户的状态从i转变为j的时间就是1个单位时间；二是客户的当前状态为i，在下一个时期其状态为K，然后，由K转变为j，此时，客户状态从i转变为j的时间=1+由状态K转为j的时间。因此，客户状态首次由i转变为j的期望时间Tij可表示为：

(4)

根据图1可知，对于T15，处于接触期的客户其状态转化为流失客户的路径主要有两条：一是下一时期，客户状态直接由接触期客户转化为流失客户；二是客户在下一时期，客户状态由接触期客户转化为成长期客户，然后在后续时期中再由成长期客户转化为流失客户。在此基础之上，依据式(4)可得到T15的表达式：

(5)

以此类推，可得到T25，T35和T45的表达式：

(6)

(7)

(8)

通过求解式(5)～式(8)所构成的方程组，即可得到接触期、成长期、成熟期和衰退期客户的剩余生命周期T15、T25、T35和T45。

3 实证分析

现有江西某电信运营商2015年7月至2015年12月部分校园动感地带客户的状态转化数据，如表1所示。

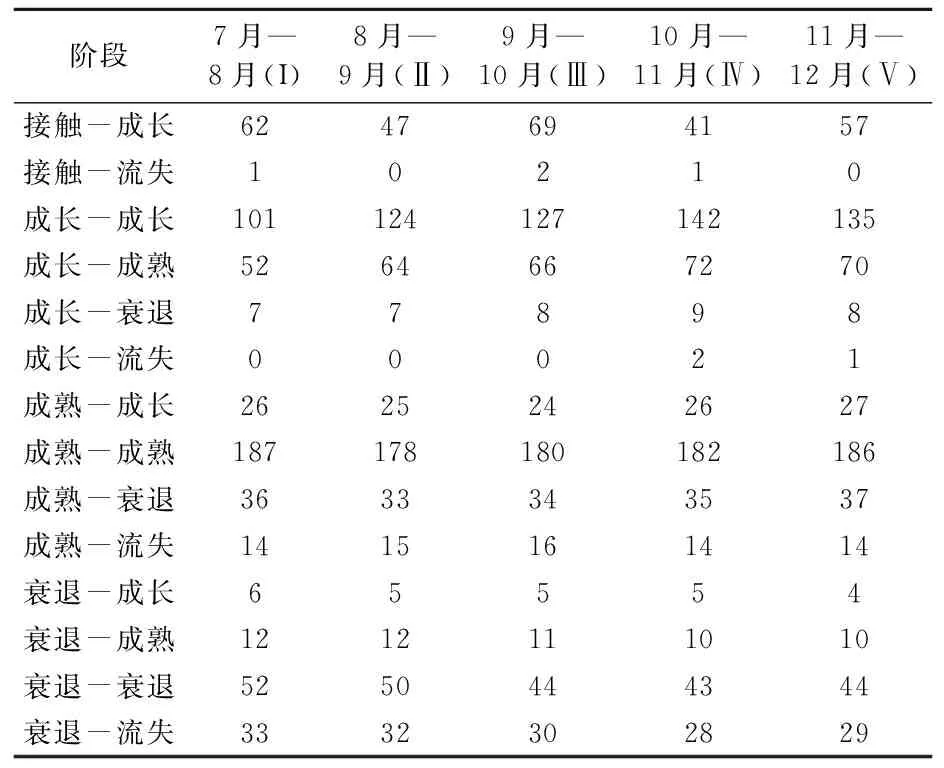
表1 客户状态分布信息表

根据式(1)～式(3)，结合表1中的客户状态转化数据，可计算出7月至12月之间的客户状态转化概率矩阵P*，具体过程如下：

根据式(1)可算得在阶段I，接触期客户转化为成长期客户的状态转化概率pI,12和接触期客户转化为流失客户的状态转化概率pI,15。

对于接触期的客户而言，其状态只能转化为成长期客户或是流失客户。因此，pI,11=0，pI,13=0，pI,14=0。此时，在阶段I，接触期客户的状态转化概率向量PI,1可表示为：PI,1=(pI,11,pI,12,pI,13,pI,14,pI,15)=(0.000,0.984,0.000,0.000,0.016)。以此类推，可得到在阶段I，成长期、成熟期和衰退期客户的状态转化概率向量分别为：PI,2=(0.000,0.631,0.325,0.044.0.000),PI,3=(0.000,0.099,0.711,0.044.0.053)，PI,4=(0.000,0.058,0.117,0.505.0.320)。

在此基础之上，根据式(2)可得到阶段I中客户的状态转化概率矩阵PI。

重复PI的计算过程，可计算出在阶段Ⅱ～阶段Ⅴ的客户状态转化概率矩阵分别为：

根据式(3)可计算出客户在阶段Ⅰ～阶段Ⅴ期间的状态转化概率矩阵P*。

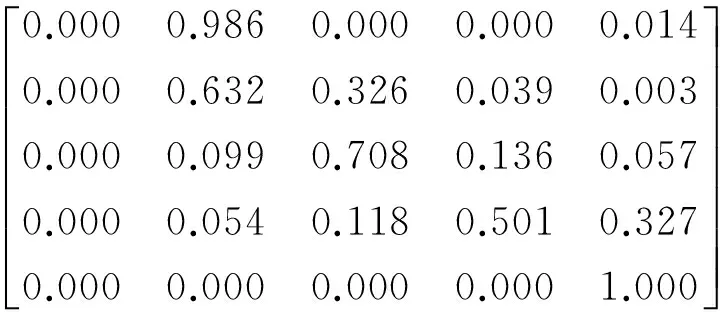
在P*的基础之上，依据式(5)～式(8)可得到接触期、成长期、成熟期、衰退期客户的剩余生命周期分别为：

1+0.326T35+0.039T45+0.632T25

1+0.136T45+0.708T35+0.099T25

1+0.501T45+0.054T25+0.118T35

运用Matlab7.0求解上述由T15，T25，T35及T45表达式所构成的方程组，可得到：T15≈13.4，T25≈12.5，T35≈10.4，T45≈5.8。该结果说明此时系统中处于接触期客户的剩余生命周期约为13.4个月，处于成长期客户的剩余生命周期约为12.5个月，处于成熟期客户的剩余生命周期约为10.4个月，处于衰退期客户的剩余生命周期约为5.8个月，在实际情形中，校园动感地带客户一般为学生客户，学生客户的生命周期一般是12～15个月，因此模型的测算结果与现实情形相吻合。

4 结论

客户的剩余生命周期对客户价值的度量有重要的意义，笔者在客户生命周期理论的基础之上，分析了生命周期各阶段客户的状态转化过程，并确定了客户在整个生命周期中的状态转化过程实际为一个以接触期为起点，流失期为吸收态，成长期、成熟期及衰退期3个状态能够相互转化的马尔可夫链，并根据马尔可夫链中首次通过时间的计算思想得到了生命周期各阶段客户剩余生命周期的计算方法。最后以江西某电信运营商的客户数据对该方法进行了实证，结果表明笔者的方法可以有效地对客户的剩余生命周期进行计算。

[1] 辛宇，郑鑫.大数据驱动与客户生命周期：基于汽车行业的分析[J].河南社会科学，2014,22(3):71-77.

[2] 郭磊，胡安安，黄丽华.客户价值计算理论的研究评述与展望[J].经济问题探索，2014(10):154-161.

[3] 李菁菁，邵培基，严博.个体客户生命周期价值的模型和实证研究[J].管理学报，2010,7(4):542-546.

[4] 齐佳音，马君，肖丽妍，等.考虑客户风险修正的客户终生价值建模型[J].管理工程学报，2015,29(2):149-159.

[5] 贺昌政，孔力.基于CLV要素的信用卡客户细分模型[J].统计与决策，2013(11):183-185.

[6] DWYER F R, SCHURR P H, OH S. Developing buyer-seller relationships[J]. The Journal of Marketing, 1987,51(4):11-27.

[7] 陈明亮.客户生命周期模式研究[J].浙江大学学报(人文社会科学版)，2002,32(6):66-72.

[8] 方蕾，王金桃. 数据挖掘在客户生命周期中的应用研究[J].武汉理工大学学报(信息与管理工程版)，2008,30(4):613-615.

[9] 陈双飞.大数据时代图书馆基于服务生命周期的客户关系管理研究 [J].现代情报，2014,34(5):91-93.

[10] 李天.基于客户生命周期理论的移动数据业务客户需求影响因素实证研究[D].北京:北京邮电大学，2013.

[11] MA M, LI Z, CHEN J. Phase-type distribution of customer relationship with Markovian response and marketing expenditure decision on the customer lifetime value [J]. European Journal of Operational Research, 2008,187(1):313-326.

[12] 朱磊，石慧，吴瑾.马尔可夫预测在IT项目进度管理中的应用[J].武汉理工大学学报(信息与管理工程版)，2009,31(4):625-628.

WANG Rui:Lect.; School of Economics and Management, Jiangxi University of Science and Technology, Ganzhou 341000, China.

Research on the Measurement Method of Customer Residual Life Cycle Based on Markov Chain

WANGRui,LIBing,LIUQin

Customer remaining life cycle has an important significance to the estimation of the customer value. However, there is a lack of research on this field at present. Therefore, an algorithm for customer remaining life cycle based on Markov chain is presented. At first, the customer state transition space is analyzed. Secondly, the state transition process of the customers that are at different stage of the life cycle is determined Then.,the Markov chain with unilateral loss wall is used to analyze the state transition process of the customer in the life cycle. Thirdly, the customer's remaining life cycle is calculated by the first-passage-time in Markov chain. At last, the validity of the algorithm is verified by the customer data of a telecom operator in jiangxi province.

customer remaining life cycle; Markov chain; customer value

2095-3852(2017)02-0213-04

A

2016-10-20.

王锐(1982-)，湖北十堰人，江西理工大学经济管理学院讲师，博士，主要研究方向为信息与决策科学.

国家自然科学基金项目(71661013)；江西省高校人文社科青年基金项目(GL1542)；江西理工大学经管学院青年教师能力提升基金项目(jgxy201502)；江西理工大学博士基金项目(jxxjbs16028)；湖北省软科学基金项目(2016ADC024).

F270；TP301

10.3963/j.issn.2095-3852.2017.02.019