基于Pitzer模型的复合盐水完井液低温相平衡计算
2017-05-10赵志强陈缘博易勇
赵志强, 陈缘博, 易勇
基于Pitzer模型的复合盐水完井液低温相平衡计算
赵志强, 陈缘博, 易勇
(中海油田服务股份有限公司油田化学研究院,河北燕郊 065201)
赵志强,陈缘博,易勇.基于Pitzer模型的复合盐水完井液低温相平衡计算[J].钻井液与完井液,2017,34(2):126-130.
ZHAO Zhiqiang, CHEN Yuanbo, YI Yong.Calculating low temperature phase equilibrium of NaCl-KCl-CaCl2completion fluid based on pitzer model[J].Drilling Fluid & Completion Fluid,2017,34(2):126-130.
结晶点是混合盐水完井液的主要性能指标,绝大部分文献和手册只提供了单盐的结晶点数据,混合盐数据只有通过实验才能得到。通过数学模型计算混合盐水的结晶点可省去大量的实验工作,并为完井液组成优化提供依据。采用Pitzer模型和Spencer模型参数进行了完井液常用的NaCl、KCl和CaCl2的单盐及二元混合盐体系的固液相平衡计算。通过文献数据和实验数据验证了计算结果的可靠性。验证结果表明,在25 ℃以下时,计算值与文献值的相对标准偏差均小于0.1,能够满足完井液研究和施工设计的需要;25 ℃以上时,KCl的单盐体系计算偏差变大,需调整KCl的Pitzer参数再进行相平衡计算。
完井液;相平衡;低温;Pitzer模型;Spencer模型参数;固液相平衡
盐水完井液的结晶点是评价完井液性能的重要指标。在给定密度下,复合盐水完井液有多种组成配方。选择结晶点过低的配方会导致材料成本上升,选择结晶点过高的配方会导致盐结晶析出,尤其是地面温度较低或海上钻井时,盐析会导致钻井管线、防喷器及泥浆池等设备的阻塞,有必要研究盐水组成与固-液相平衡之间的关系变化,从而优化完井液施工设计。NaCl、KCl和CaCl2是配制完井液常用的盐类。一些文献[1-2]和手册[3]提供了其单一盐水及部分混合盐水固-液相平衡的测定结果。但在全部组成范围内,对溶液成分与结晶点关系的研究较少。诸多理论模型依据热力学平衡原理对电解质水溶液中固-液相平衡的规律进行了研究。大量应用和检验表明,其中的Pitzer电解质溶液理论对于零至高浓度电解质溶液中固-液相平衡的预测是迄今为止最为有效的理论工具[4-7]。笔者采用变温Pitzer模型对NaCl-KCl-CaCl2溶液的结晶点进行编程计算,并与文献数据对比,取得了满意的结果。
1 Pitzer模型及模型参数
Pitzer模型是Debye-Huckel方程的发展,是一个计算电解质溶液中各组分活度系数的半经验模型。相关文献[3]对其进行了详细介绍,如公式(1)~公式(3)所示。式中,m为离子的质量摩尔浓度,mol/kg;I为电解质的离子强度,mol/kg;AΦ为Debye-Huckel斜率,mol0.5/kg0.5;Φ为水的渗透系数,无量纲;γ为离子活度系数,无量纲;Φij
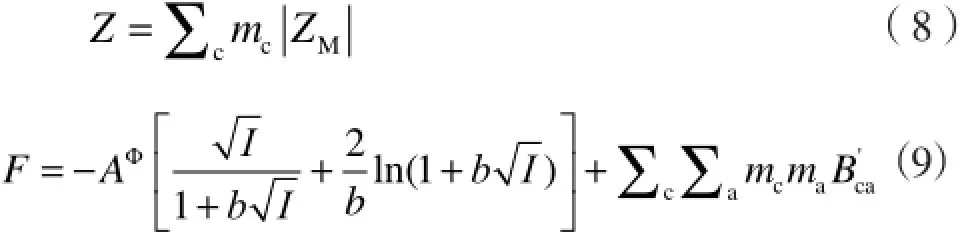
式中,β(0)、β(1)、β(2)和CΦ为Pitzer模型参数;α1和α2为方程系数,对于阴离子为-1价电解质时,α1=2.0,β(2)=0;阴离子为-2以上价态时,α1=1.2,α2=14.0;Z为总电荷系数,无量纲。
用Pitzer模型计算电解质溶解度的原理是:当电解质在水溶液中达到固-液相平衡时,电解质在固液两相的化学势相等,其平衡表达式如下:

式中,αM、αX和αW分别为阳、阴离子及水在固-液相平衡时的活度,其值为离子浓度与离子活度系数的乘积,K为相平衡常数,为温度的函数,ν+和ν-分别为1 mol电解质电离产生的阳、阴离子物质的量分数,n为结晶固相所含结晶水的数。将Pitzer模型方程代入到式(10),便可计算出一定组成溶液所对应的结晶点。Pitzer模型计算所涉及到的参及为离子的二元混合函数,是离子强度I的函数,可近似为常数θ;ψ为离子的三元混合参数。ZM和ZX为阳离子及阴离子的电荷数。b为模型系数,无量纲,一般取1.2;下标c和M表示阳离子,下标a和X表示阴离子。其他未知量的计算分别见公式(4)~公式(9)。数β(0)、β(1)、CΦ、θ和Ψ,以及AΦ、lnK均与温度有关。Spencer等[8]通过数据拟合,建立了这些参数与温度的函数关系式:


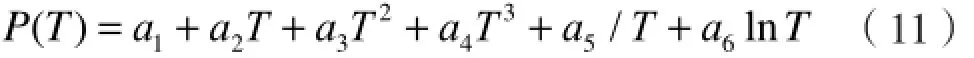
式中,a1~a6为方程系数,其值见表1及表2。笔者利用这些关系式进行了NaCl-H2O、KCl-H2O、CaCl2-H2O二元体系以及NaCl-KCl-H2O、NaCl-CaCl2-H2O、KCl-CaCl2-H2O三元体系的固-液相平衡计算。

表1 NaCl-KCl-CaCl2- H2O体系的平衡常数lnK方程系数

表2 NaCl-KCl-CaCl2的Pitzer参数方程系数
2 单一电解质溶液结晶点预测
2.1 NaCl-H2O体系
采用Pitzer模型进行了NaCl-H2O体系的相平衡计算。固液平衡曲线的计算结果如图1所示,图中实测数据取自文献[3]和文献[5]。与文献[3]的14个数据点和文献[5]的13个数据对比,在给定温度下,NaCl浓度计算值与文献值的相对标准差分别为0.005 8和0.003 7。文献[3]和文献[5]给出的水石盐-冰共晶浓度为23.34 %,共晶点分别为-21.1 ℃和-21.48 ℃,而模型计算的共晶浓度为23.24%,共晶点为-21.45 ℃。计算值与实际值吻合较好。
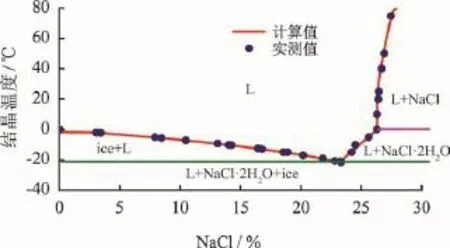
图1 NaCl-H2O体系固液平衡相图
2.2 KCl-H2O体系
KCl-H2O体系的固液平衡曲线计算结果如图2所示。图2中实测数据分别为文献[8]的12个数据点和文献[3]的11个数据点。

图2 KCl-H2O体系固液平衡相图
在给定温度下,KCl浓度计算值与文献[8]和文献[3]值的相对标准差分别为0.031和0.043。文献给出的钾石盐-冰共晶浓度分别为19.9%和20%,共晶点分别为-10.6 ℃和-10.8 ℃,而模型计算的共晶浓度为19.70%,共晶点为-10.83 ℃。当温度大于25 ℃时,计算值与实际值偏差较大,需重新调整Pitzer参数方可准确计算。
2.3 CaCl2-H2O体系
图3为CaCl2-H2O体系的计算结果,图中实测数据分别为文献[3]的25个数据点和文献[5]的12个数据点。在给定温度下,CaCl2浓度计算值与文献[3]和文献[5]的相对标准差分别为0.006 7和0.027。计算的南极石-冰的共晶浓度为30.69%,共晶温度为-50.35 ℃,而文献[3]给出的共晶浓度为30.55%,共晶温度为-49.8 ℃,计算值与文献值偏差较小。

图3 CaCl2-H2O体系固液平衡相图
3 混合电解质结晶点预测
3.1 NaCl-KCl-H2O体系
对NaCl-KCl-H2O体系进行了固液相平衡计算,并绘制了-20~20 ℃的等温曲线,其结果如图4所示。当温度高于0 ℃时,图中曲线上方为固液共存区,下方为液相区;当温度低于0 ℃时,曲线与坐标轴围成的封闭区域为液相区,其他区域为固液共存区。图中实测数据取自文献[3]。对比结果表明,在-20~20 ℃范围内,NaCl浓度计算值的相对标准偏差为0.013,KCl浓度计算值的相对标准偏差为0.047。计算得水石盐-钾石盐-冰的共晶温度为-23.2 ℃,NaCl和KCl的共晶浓度分别为5.62 %和20.50%。而文献[4]报道的共晶温度为-23.7~-22.9 ℃,NaCl共晶浓度为19.3%~20.26%、KCl共晶浓度为5.49%~6.39%。共晶温度偏差在0.5 ℃以内,可以满足完井液施工设计需要。

图4 NaCl-KCl-H2O体系固液平衡等温曲线
3.2 NaCl-CaCl2-H2O体系
固定NaCl与CaCl2质量百分比浓度的比值,计算不同浓度NaCl下混合盐水的结晶点,计算结果与文献[5]数据进行了比较,结果如图5所示。

图5 NaCl-CaCl2-H2O体系结晶点计算结果
计算的94个数据点,其结晶点的相对标准偏差为0.067。在低浓度范围内计算值与文献测量值吻合较好;高浓度时,计算结果略高于文献值。r=0.203时偏差较大,在1.54~3.38 ℃之间,剔除r=0.203时的9个数据点,相对标准偏差降低至0.052。计算得水石盐-南极石-冰的共晶温度为-51.7 ℃,NaCl的共晶浓度为1.94%,CaCl2的共晶浓度为29.09%,该共晶点无测量数据参考。
3.3 KCl-CaCl2-H2O体系
图6为KCl-CaCl2-H2O体系的等温曲线。当温度高于0 ℃时,图中曲线上方为固液共存区,下方为液相区;当温度低于0 ℃时,曲线与坐标轴围成的封闭区域为液相区,其他区域为固液共存区。该体系可供参考的测量数据较少,文献[4]给出了0 ℃和25℃的13个测量数据点。计算得KCl浓度相对标准偏差为0.087,CaCl2浓度相对标准偏差为0.14。0 ℃的计算值与测量值吻合较好,相对标准偏差分别为0.032和0.073,25 ℃时偏差较大。这与25 ℃以上时,KCl-H2O体系计算偏差变大相一致。计算得钾石盐-南极石-冰的共晶温度为-50.95 ℃,KCl的共晶浓度为1.63%,CaCl2共晶浓度为30.24%,该共晶点无测量数据参考。

图6 KCl-CaCl2-H2O体系固液平衡等温曲线
4 结论
1.采用Pitzer模型和Spencer模型参数,进行了NaCl、KCl和CaCl2的单盐及混合盐体系固液相平衡计算,计算结果可作为盐水完井液研究和施工设计的参考依据。
2.计算结果与部分文献实测值进行了对比,结果表明:除KCl-CaCl2-H2O体系25 ℃时的数据外,其他体系的浓度相对标准偏差值均小于0.1;25 ℃以上时,KCl计算偏差变大,需优化KCl在25 ℃以上的Pitzer参数;25 ℃以下时,计算偏差较小,可满足完井液研究和施工设计需要。
[1]HOOMAN H, ANTONIN C, BAHMAN T. Freezing point depression of electrolyte solutions: experimental measurements and modeling using the CPA equation of state[J]. Industrial & Engineering Chemistry Research,2008, 47(11):S20–S22.
[2]岳前升, 杨青志, 陈军,等. 无机盐和有机盐对盐膏层溶解性的影响[J]. 钻井液与完井液,2013, 30(3):31-33.
YUE Qiansheng, YANG Qingzhi, CHEN Jun, et al. Influence of inorganic and organic salt on solubility of gypsum[J]. Drilling Fluid & Completion Fluid, 2013,30(3) :31-33.
[3]牛自得, 程芳琴. 水盐体系相图及其应用[M].天津:天津大学出版社, 2005:186-190.
NIU Zide, CHENG Fangqin. Phase diagrams and applications of salt-water system[M].Tianjin: Tianjin university press, 2005:186-190.
[4]孙海霞,曹红翠,保英莲,等. 基于Pitzer模型的25℃KCl-CsCl-H2O体系溶解度预测研究[J]. 西南民族大学学报(自然科学版),2014,40(1):54-57.
SUN Haixia, CAO Hongcui,BAO Yinglian,et al. Solubility prediction in the systems of KCl-CsCl-H2O at 25 ℃ using Pitzer ion-interaction model[J].Journal of Southwest Uniνersity for Nationalities(Natural Science Edition, 2014,40(1): 54-57.
[5]CHI GUOXIANG, CHU HAIXIA,RYAN SCOTT,et al. New method for determining fluid compositions in the H2O-NaCl-CaCl2System with Cryogenic Raman Spectroscopy[J]. Acta Geologica Sinica(English Edition), 2014, 88(4): 1169-1182.
[6]RONALD J BAKKER,MIRIAM BAUMGARTNER. Unexpected phase assemblages in inclusions with ternary H2O-salt fluids at low temperatures[J].Open Geosciences,2012,4(2):225-237.
[7]SPENCER R J,MOLLER N,WEARE J H.The prediction of mineral solubilities in natural water: A chemical equilibrium model for the Na-K-Ca-Mg-Cl-O system at temperature below 25 ℃[J]. Geochim Cosmochim Acta,1989, 54(3): 575-590.
[8]SANJOY K. BHATTACHARIA, NAZIR HOSSAIN,et al. Thermodynamic modeling of KCl+H2O and KCl+NaCl+H2O systems using electrolyte NRTL model[J].Fluid Phase Equilibaia, 2015, 403( 2015): 1-9.
Calculating Low Temperature Phase Equilibrium of NaCl-KCl-CaCl2Completion Fluid Based on Pitzer Model
ZHAO Zhiqiang, CHEN Yuanbo, YI Yong
(Oilfeld Chemical Research Institute of COSL, Yanjiao, Hebei 065201)
Crystallization point, a main performance index of composite brine completion fuids, can only be obtained through laboratory experiments because most of the articles and handbooks only give the crystallization point of the single salt. If the crystallization point of a composite brine can be calculated with mathematical model, then large amount of tedious experiment can be saved, and the optimization of composite brine completion fuid can be achieved using the calculated data. Using the Pitzer model and the Spencer model parameters, salts commonly used in completion fuids, such as NaCl, KCl and CaCl2, were calculated for their solid-liquid phase equilibrium both as single salt and binary salts. The liability of the calculation was verifed using documented data and experiment data. It was shown that at temperatures below 25 ℃, the relative standard deviation between the calculated values and the documented data was less than 0.1, satisfying the need for completion fuid study and design. At temperatures above 25 ℃, the relative standard deviation for KCl became larger, and the Pitzer parameters of KCl needed to be adjusted for phase equilibrium recalculation.
Completion fuid; Phase equilibrium; Low temperature; Pitzer model; Spencer model parameter; Solid-liquid phase equilibrium
TE254.3
A
1001-5620(2017)02-0126-05
2016-12-14;HGF=1702N5;编辑 王小娜)
10.3969/j.issn.1001-5620.2017.02.023
中海油田服务股份有限公司项目“南海西部油水井修井解堵技术研究”(YHB15YF001)。
赵志强,1980年生,中级工程师,现在从事钻完井液材料与技术研发工作。电话 (0316)3367048;E-mail:zhaozhq4@cosl.com.cn。
