贮箱Y形环焊接残余应力及其对承载行为的影响

李艳军，吴爱萍，刘德博，赵海燕，赵 玥，王国庆



贮箱Y形环焊接残余应力及其对承载行为的影响

李艳军1，吴爱萍1，刘德博2，赵海燕1，赵 玥1，王国庆3

(1．清华大学机械工程系摩擦学国家重点实验室先进成形制造教育部重点实验室，北京 100084；2．北京宇航系统工程研究所，北京 100076；3. 中国运载火箭技术研究院，北京 100076)

为了阐明贮箱Y形环环缝焊接残余应力对其承载行为的影响，以大型运载火箭贮箱Y形环为研究对象，采用数值模拟计算得到Y形环与箱筒段环缝焊后残余应力；然后分别在考虑和不考虑残余应力情况下，进一步计算Y形环承受内压载荷时的应力分布。结果表明：环缝焊接在接头区域产生很大的残余应力，最大等效应力位于部分熔化区，最大值达到358 MPa；焊接残余应力对远离接头的部位承载时的应力基本没有影响，主要导致接头区域的应力提高，且使Y形环承载时的等效应力最大值也略有增大；焊接残余轴向应力和内压产生的轴向应力在接头内表面都是拉应力，两者叠加导致轴向拉应力明显增大。

贮箱；Y形环；残余应力；数值模拟；焊接

推进剂贮箱是运载火箭箭体结构中非常重要的结构部件，既是贮存液氢/液氧的压力容器，又是运载器的主要承力结构，具有支撑防护系统以及为其他系统仪器设备提供安装基础和空间的作用[1]。贮箱主要采用高强铝合金材料经拼装焊接而成，一般由过渡环、箱底、箱筒段和短壳等部件组成。其中，过渡环是箱底、箱筒段和短壳的连接结构，从设计方案上分为叉形环和Y形环[2]。Y形环受箱体内压、箭体结构轴压/拉、弯矩的共同作用，导致此处受力复杂，同时Y形环通过焊接方式与其他部件连成整体[3−5]。贮箱主要采用高强铝合金(如2219-T87)制造，该材料采用熔化焊焊接时焊缝、部分熔化区和过时效区均是力学性能薄弱区，接头拉伸时主要断裂在焊缝和部分熔化区，故焊接接头是贮箱承载时的薄弱环节[6]。可见，Y形环与箱筒段连接处既承受复杂的载荷又存在焊接薄弱环节。另外，Y形环与箱筒段的焊接在贮箱制造中一般是最后焊接的焊缝，所以还存在较大的焊接残余应力。由于结构大而且复杂，Y形环与箱筒段焊接残余应力的分析和测试都存在较大的困难，对于此焊道焊接产生的残余应力及其对承载行为的影响一直未能得到很好的认识。因此，本研究的目的主要为阐明大型运载火箭贮箱Y形环的焊接残余应力分布及其对连接环承载行为的影响规律，为Y形环的设计及实际应用提供指导依据。

基于有限元方法的数值模拟技术可以用较低的成本来考察焊接应力、应变的演变过程，已经大量应用于预测焊接残余应力与变形的研究工作中[7−10]，并开始在实际工程实践中发挥作用[11−13]。本文作者首先对Y形环和箱筒段之间的环缝焊接过程进行了数值分析，获得了焊后残余应力的分布规律；然后对比研究了在考虑和不考虑残余应力情况下承受内压载荷时Y形环的应力分布规律，从而获得残余应力对Y形环承载行为的影响。

1 有限元分析模型

1.1 几何模型与网格划分

本模拟中以大型运载火箭贮箱Y形环与箱筒之间的环缝为研究对象，因贮箱结构尺寸大，且考虑到结构的对称性，为了提高计算效率，建立了45°局部计算模型进行分析，如图1所示。本研究中旨在分析Y形环与箱筒之间的环缝焊接残余应力及其对Y形环承载行为的影响，因此，该计算模型只包含了Y形环及部分的箱筒、箱底、短壳等结构。另外，Y形环在过渡区外侧环向均布了160个质量减轻凹孔且在内表面设计了凹槽。采用8节点六面体单元对几何体进行网格划分，焊缝及其附近区域网格尺寸较细，轴向及径向尺寸约为1~2 mm，周向为3.5 mm；远离焊缝区域网格的周向尺寸为14 mm，网格轴向尺寸也逐渐增大到14 mm。该模型网格总数为405533个，节点总数为487089。

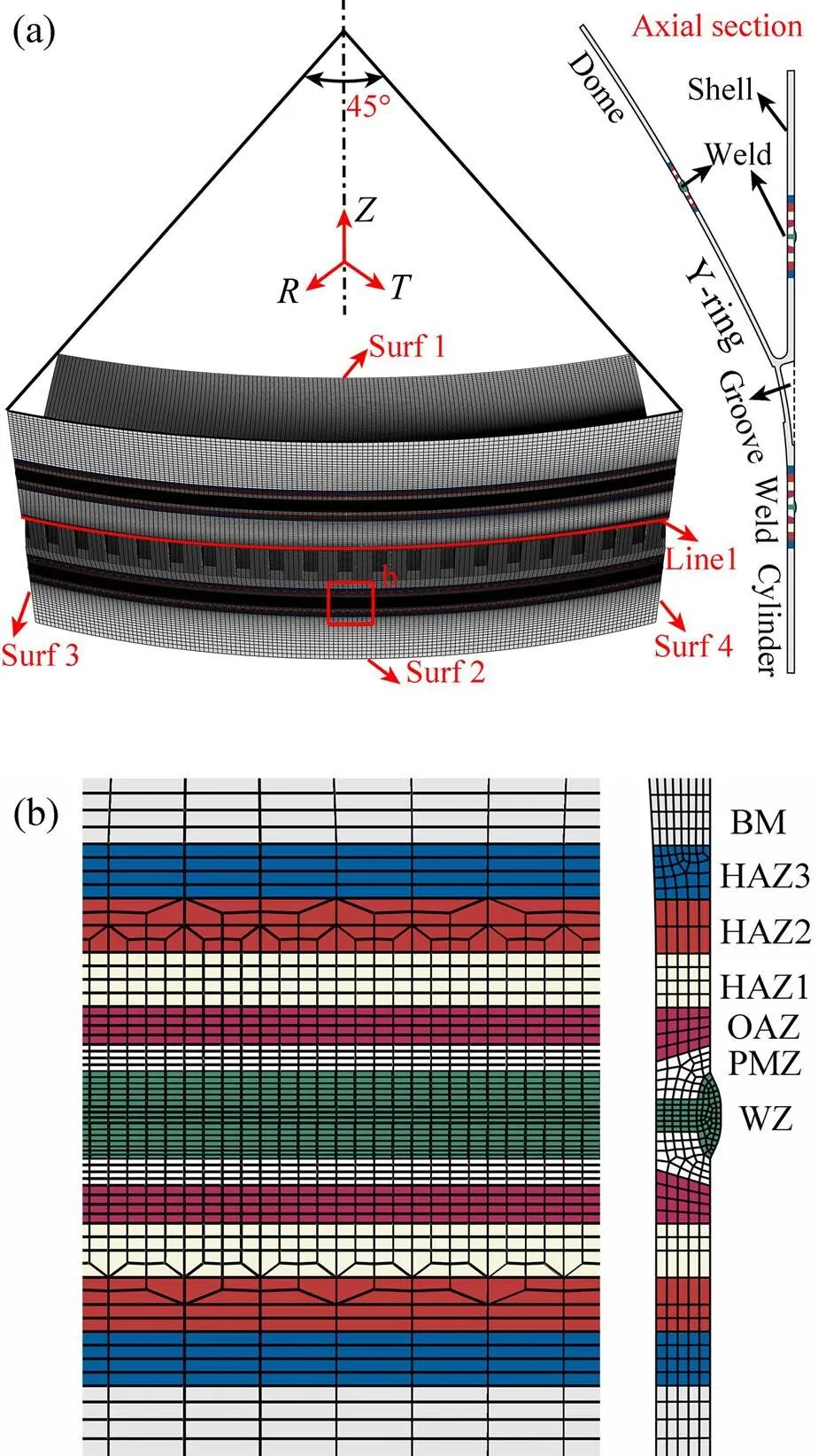
图1 Y形环有限元模型

1.2 材料性能参数

该贮箱所用材料为2219-T87铝合金，材料热物理性能和力学性能参数均随温度变化，如图2所示。其中，400 ℃左右以下热物理性能和弹性模量、泊松比的数据通过查阅文献[14−16]归纳得到(见图2(a)、2(b)中的实线部分)，400 ℃以上的数据按照变化趋势外延得到(见图2(a)、2(b)中的虚线部分)。计算温度场时，熔点以上温度通过人为增加热导率来考虑熔池的对流热扩散作用。

2219-T87铝合金焊接后接头的力学性能分布很不均匀，根据测试研究结果将接头分为焊缝区(WZ)、部分熔化区(PMZ)、过时效区(OAZ)、热影响区1(HAZ1)、热影响区2(HAZ2)、热影响区3(HAZ3)及母材(BM)等7个区域，各区域划分及其尺寸是根据平板对接焊接头横截面上的显微组织变化和硬度分布而确定[17](见图1(b))。其中，由于环缝焊接采用变极性钨极氩弧焊进行打底和盖面两道焊接，焊缝区表现为T字形。各区域室温下的屈服应力由实验获得[17]，而母材屈服强度随温度变化的规律参考文献[15]获得，按照母材屈服强度随温度变化的规律设定其他区域的屈服强度随温度变化的规律(见图2(c))，并通过平板对接案例验证，计算时加热过程按母材性能随温度变化、冷却过程按各区的性能曲线随温度变化。

图2 材料性能随温度的变化曲线

1.3 边界条件及加载

焊接残余应力模拟采用单向热−力耦合计算方法，先计算焊接温度场，然后将焊接温度场模拟结果以热载荷的方式加载到应力计算模型中求解应力与应变。在温度场计算过程中，为了提高计算效率，对热源加载方式进行简化：沿周向将焊道平分为小段，然后通过逐段加热来模拟热源移动，考虑到计算效率及精度，本模型中取40；对于每一小段而言，采用等密度的体积热源来模拟焊接热输入，其横截面面积与对应焊缝截面面积大致相等，并通过试计算，使熔池横截面形貌尺寸与焊缝相当、热影响区分布也与实际接近。模型表面的散热按照一般空气条件下的等效对流换热处理[18]，环境温度设为20℃。

计算应力变形时不考虑卡具拘束作用。研究表 明[12]，对于旋转周期对称结构，采用45°局部三维、边界假设为无周向位移模型代替360°模型是可行的。因此，本模拟中边界面Surf 3和Surf 4(见图1(a))上施加周向位移约束；另外在模型周向上选取一条线(line1)，将其轴向拘束住，从而限制了模型的刚性平动和转动。

贮箱设计内压载荷为0.771 MPa，计算Y形环在承受该内压载荷下的应力分布时，模型的拘束条件与上述条件相同。内压载荷通过在边界上设置相应的力学载荷从而施加在模型上：在模型内表面施加 0.771 MPa的压力，在Surf 1和Surf 2上施加相应的正应力和径向切应力，其中，径向切应力大小为0.771 MPa，方向沿径向向内，而正应力为拉应力，大小由式(1)确定：

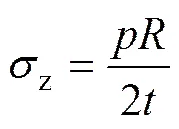
式中：为内压；是相应位置的半径；为壁厚。

2 结果与讨论

为了对比不同条件(焊态、焊态+内压、内压)下应力分布的区别，在模型中部选取了具有代表性的纵切面上的应力分布来进行比较。图3所示为不同条件下纵切面上等效应力分布云图，由图3(a)可见，焊产生了很大的残余应力，主要分布在焊缝及其附近区域，等效应力最大值为358 MPa，位于接头的部分熔化区；焊缝及其他热影响区内的应力水平大约为150~230 MPa；另外，Y形环内表面的残余应力比外表面的残余应力要大。焊后施加内压后的等效应力分布如图3(b)所示，在残余应力存在的基础上施加0.771 MPa的内压载荷后，Y形环过渡区内表面的应力水平大大提高，等效应力最大值为357.3 MPa，位于内表面凹槽箱筒侧端部(见图3(b)中箭头所示)。另外，施加内压载荷后，接头外表面附近的等效应力水平有所降低，而内表面的等效应力无明显变化。图3(c)所示为Y形环不考虑焊接残余应力情况下施加内压载荷时的应力分布，Y形环的等效应力最大值为354.0 MPa，位于内表面凹槽箱筒侧端部，而远离过渡区的应力水平较低，焊接接头区域(焊缝和部分熔化区)的等效应力不到120 MPa。上述分析结果表明：焊接在接头处产生了很大的残余应力，尤其是部分熔化区，产生的等效应力已接近断裂应力(398 MPa[15])。焊接残余应力对远离接头部位(箱底和短壳)的应力分布基本没有影响，主要对Y形环过渡区和接头附近的应力分布有影响，焊接残余应力使Y形环承受内压载荷时的等效应力最大值略微增大了3.3 MPa。

图3 Y形环纵切面等效应力分布

图4所示为不同条件(焊态、焊态+内压、内压)下上述纵切面上Y形环与箱筒接头区域的内外表面应力沿轴向的分布。可见残余应力主要分布在离焊缝中心40 mm以内的范围。其中，焊缝区等效应力最大值为146MPa，部分熔化区等效应力最大值达到了358 MPa，过时效区及热影响区(HAZ1、HAZ2)也存在较大残余应力，其等效应力最大值分别达到了240、230 MPa。环缝焊接在焊缝及其附近区域产生了很大的周向拉应力，部分熔化区的拉应力最大，内表面最大值达到389 MPa；焊缝区内表面周向应力最大值为165 MPa，过时效区及热影响区(HAZ1、HAZ2)分别为275、258 MPa；外表面的周向应力相对较小，部分熔化区外表面最大值为198 MPa，焊缝区最大值仅为70 MPa，过时效区及热影响区周向应力范围大约为100~173 MPa。另外，内表面轴向应力为拉应力，最大值为114 MPa，位于箱筒侧热影响区；而外表面为压应力，最大值为−100 MPa，位于Y形环侧焊趾。焊后施加内压载荷时，接头内表面的等效应力变化较小，部分熔化区略有降低，但其他区域的等效应力略有增大，外表面的等效应力明显降低；接头内表面的周向拉应力略有降低，外表面上焊缝及Y形环侧的周向应力也有所降低，但箱筒侧过时效区、热影响区的周向应力却有所提高；内表面的轴向应力明显增大，而外表面上Y形环侧的轴向压应力增大，箱筒侧的轴向应力由压应力转变为拉应力，但大小有所降低。

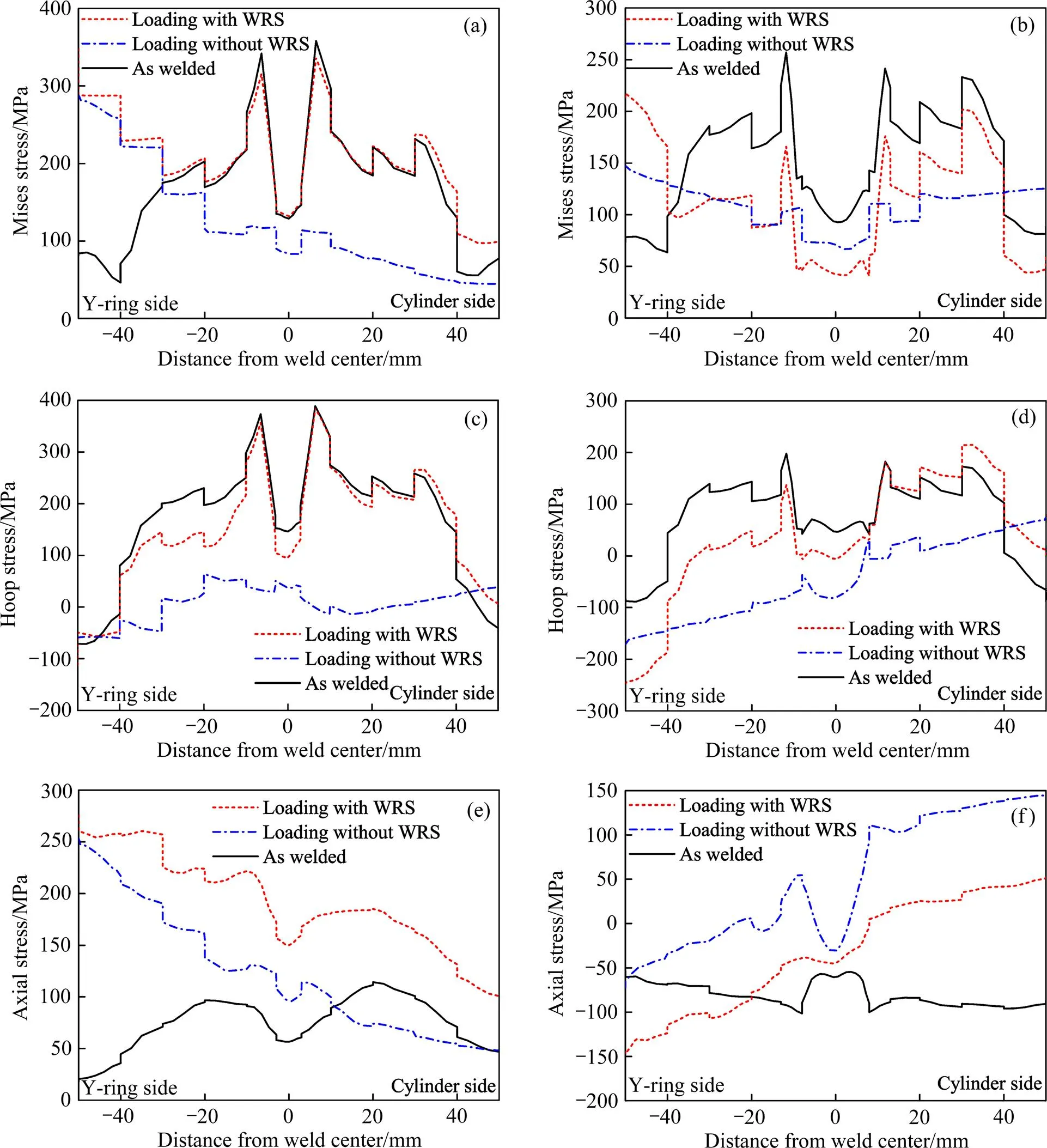
图4 Y形环与箱筒段接头区域应力沿轴向分布

不考虑焊接应力、施加内压载荷时，接头的等效应力较小，焊缝区、部分熔化区和过时效区的等效应力最大值为分别为87、120和110 MPa，都位于外表面；内表面的周向应力很小，外表面由Y形环侧的压应力逐渐增大为拉应力且应力值也不大；内表面的轴向应力为拉应力(焊缝区、部分熔化区和过时效区的最大值分别为108、131和138 MPa)，外表面的轴向应力由Y形环侧的压应力逐渐转变为箱筒侧的拉应力。通过对比考虑与不考虑焊接应力两种情况下Y形环施加内压载荷时的应力分布可知，焊接残余应力对接头附近的应力分布影响很大，内表面的等效应力和周向应力分布主要取决于焊接残余应力，因为内压在内表面产生的等效应力和周向应力均很小；另外，考虑焊接残余应力时，箱筒侧外表面的等效应力和周向应力也都增大。焊接残余应力的存在使内表面的轴向拉应力明显增大，这是因为焊接和内压在内表面产生的轴向应力都是拉应力，两者叠加导致轴向拉应力增大；外表面Y形环侧的轴向压应力增大而箱筒侧的周向拉应力减小，这是由于内压在外表面上产生的轴向应力由压应力(Y形环侧)转变为拉应力(箱筒侧)，焊接残余轴向应力为压应力，两者叠加导致上述变化。

图5所示为接头内表面等效塑性应变沿轴向的分布，由图5(a)可知，焊后接头存在较大的残余塑性应变，尤其在部分熔化区。焊后施加0.771 MPa的内压载荷时，部分熔化区的等效塑性应变基本不变，而焊缝、过时效区、热影响区1和热影响区2的等效塑性应变均比残余等效塑性应变略有增大；图5(b)所示为加载时导致的等效塑性应变增量。由图5(b)可见，部分熔化区靠近过时效区侧的等效塑性应变增量基本上是零，而在其他区域均大于零，其中过时效区和热影响区1的塑性应变增量较大。该结果与等效应力的变化相符，焊后施加内压载荷时，部分熔化区内表面的等效应力比焊接残余应力略低，而其他区域比焊接残余应力还略有增大。焊缝区和过时效区是接头的薄弱区，焊接残余应力与内压载荷共同作用下，这两个区的应力将更大。

图5 接头内表面等效塑性应变及加载时等效塑性应变增量分布

3 结论

1) 采用数值模拟方法获得了Y形环与箱筒段环缝焊接残余应力，残余应力主要分布在离焊缝中心40 mm以内的范围，焊缝区等效应力最大值为146 MPa，部分熔化区等效应力最大值达到358 MPa，过时效区及热影响区(HAZ1、HAZ2)也存在较大残余应力。

2) 焊接残余应力对远离接头部位(箱底和短壳)承载时的应力分布基本没有影响，主要对接头区域及其附近的过渡区有影响，焊接残余应力使Y形环承载时的等效应力最大值略微增大3.3 MPa，而接头区域的等效应力水平取决于焊接残余应力。

3) 焊接残余轴向应力和内压产生的轴向应力在接头内表面都是拉应力，两者叠加导致轴向拉应力明显增大。

[1] 姚君山, 蔡益飞, 李程刚. 运载火箭箭体结构制造技术发展与应用[J]. 航空制造技术, 2007(10): 36−40. YAO Jun-shan, CAI Yi-fei, LI Cheng-gang. Development and application of manufacturing technologies for launch vehicle's body structure[J]. Aeronautical manufacturing technology, 2007(10): 36−40.

[2] 赵 亮. 大直径薄壁箱体结构力学分析与精细优化设计[D]. 大连: 大连理工大学, 2015: 3−7. ZHAO Liang. The mechanical analysis and refined optimization of large-diameter and thin-walled tank structures[D]. Dalian: Dalian University of Technology, 2015: 3−7.

[3] 孔德跃, 何凡锋, 王伟明, 章 勇, 吴新录. 叉形环与球形箱底环形焊接夹紧机构设计[J]. 航空制造技术, 2011(9): 93−95. KONG De-yue, HE Fan-feng, WANG Wei-ming, ZHANG Yong, WU Xin-lu. Welding and clamping mechanism design of spherical base and fork-like ring[J]. Aeronautical Manufacturing Technology, 2011(9): 93−95.

[4] 熊 焕. 低温贮箱及铝锂合金的应用[J]. 导弹与航天运载技术, 2001(6): 33−40. XIONG Huan. Cryogenic tank and application of aluminum- lithium alloy[J]. Missiles and Space Vehicles, 2001(6): 33−40.

[5] 王 博, 赵 亮, 郝 鹏, 蒋亮亮, 彭伟斌. 改善贮箱Y形环焊缝应力水平的优化设计[J]. 宇航材料工艺, 2014, 44(z1): 42−46. WANG Bo, ZHAO Liang, HAO Peng, JIANG Liang-liang, PENG Wei-bin. Optimization of improving Y-ring welding stress level for tanks[J]. Aerospace Materials and Technology, 2014, 44(z1): 42−46.

[6] 李 权. 2219铝合金熔化焊接头力学性能薄弱区研究[D]. 北京: 清华大学, 2015: 72−83. LI Quan. Investigation on the weakness region of the fusion welded joints of 2219 aluminum alloy[D]. Beijing: Tsinghua University, 2015: 72−83.

[7] 叶延洪, 何 静, 蔡建鹏, 孙加民, 邓德安. 6061-T651铝合金薄板接头的焊接变形[J]. 中国有色金属学报, 2014, 24(10): 2435−2442. YE Yan-hong, HE Jing, CAI Jian-peng, SUN Jia-min, DENG De-an. Welding deformations of 6061-T651 Al alloy thin-plate joints[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2435−2442.

[8] 鄢东洋. 铝合金薄壁结构搅拌摩擦焊热−力学过程的研究及模拟[D]. 北京: 清华大学, 2010. YAN Dong-yang. Investigation on thermo-mechanical process in friction stir welding of aluminum alloy thin-walled structure and its numerical simulation[D]. Beijing: Tsinghua University, 2010.

[9] 廖志谦, 刘希林, 周 川, 张建欣. 钛合金大厚板窄间隙焊接接头三维应力数值模拟计算[J]. 中国有色金属学报, 2010, 20(S1): s393−s398. LIAO Zhi-qian, LIU Xi-lin, ZHOU Chuan, ZHANG Jian-xin. Numerical simulation about three dimensional stress in titanium alloy heavy plate of narrow gap welded joint[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(S1): s393−s398.

[10] 邓德安, KIYOSHIMA S. 退火温度对SUS304不锈钢焊接残余应力计算精度的影响[J]. 金属学报, 2014, 50(5): 626−632. DENG De-an, KIYOSHIMA S. Influence of annealing temperature on calculation accuracy of welding residual stress in a SUS304 stainless steel joint[J]. Acta Metallurgica Sinica, 2014, 50(5): 626−632.

[11] 蔡志鹏. 大型结构焊接变形数值模拟的研究与应用[D]. 北京: 清华大学, 2001. CAI Zhi-peng. Study on numerical simulation of welding distortions in huge fabrications and its application[D]. Beijing: Tsinghua University, 2001.

[12] 任维佳. 大型电机转子焊接残余应力的数值模拟研究[D]. 北京: 清华大学, 2001. REN Wei-jia. Study on numerical simulation on the welding residual stresses of large scale electromotor rotors[D]. Beijing: Tsinghua University, 2001.

[13] FU D, ZHOU C, LI C, WANG G, LI L. Effect of welding sequence on residual stress in thin-walled octagonal pipe-plate structure[J]. Transactions of Nonferrous Metals Society of China. 2014, 24(3): 657−664.

[14] MENG Q G, FANG H Y, YANG J G, JI S D. Analysis of temperature and stress field in Al alloy's twin wire welding[J]. Theoretical and Applied Fracture Mechanics. 2005, 44(2): 178−186.

[15] KAUFMAN J G. Properties of aluminum alloys: tensile, creep, and fatigue data at high and low temperatures[M]. Materials Park, Ohio: ASM International, 1999.

[16] NARENDER K, RAO A S M, RAO K G K, KRISHNA N G. Thermo physical properties of wrought aluminum alloys 6061, 2219 and 2014 by gamma ray attenuation method[J]. Thermochimica Acta, 2013, 569: 90−96.

[17] LI Yan-jun, LI Quan, WU Ai-ping, MA N, WANG Guo-qing, MURAKAWA H, YAN Dong-yang, WU Hui-qiang. Determination of local constitutive behavior and simulation on tensile test of 2219-T87 aluminum alloy GTAW joints[J]. Transactions of Nonferrous Metals Society of China. 2015, 25(9): 3072−3079.

[18] 上田幸雄, 村川英一, 麻宁绪, 罗 宇, 王江超. 焊接变形和残余应力的数值计算方法与程序[M]. 成都: 四川大学出版社, 2008: 42−45. UEDA Y, MURAKAWA H, MA N, LUO Yu, WANG Jiang-chao. Numerical computation method and program for welding distortion and residual stress[M]. Chengdu: Sichuan University Press, 2008: 42−45.

(编辑 龙怀中)

Numerical simulation on Y-ring welding residual stress and its effects on loading behavior of propellant tank

LI Yan-jun1, WU Ai-ping1, LIU De-bo2, ZHAO Hai-yan1, ZHAO Yue1, WANG Guo-qing3

(1. The State Key Laboratory of Tribology, Key Laboratory for Advanced Materials Processing Technology, Ministry of Education, Department of Mechanical and Engineering, Tsinghua University, Beijing 100084, China;2. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China;3. China Academy of Launch Vehicle Technology, Beijing 100076, China)

According to the Y-ring of a heavy lift launch vehicle tank, the welding residual stress (WRS) between Y-ring and cylindrical shell was calculated by thermal-elastic-plastic finite element method. Then, stress distributions of the Y-ring under internal pressure loading with and without considering WRS were calculated in order to investigate the effect of WRS on loading behavior of the Y-ring structure. The results show that the WRS caused by the girth weld between Y-ring and cylindrical shell is very high, and the maximum Mises stress reaching 358MPa is located in partially melted zone. The WRS basically has little influence on stress distribution under loading in the region away from the joint, but increases the stress in the joint significantly, and also enlarges a little the maximum stress of the Y-ring under loading. In addition, the axial stresses at the inside surface generated by both the girth weld and internal pressure are tension stress, therefore the axial tension stress is obviously enlarged by the combined action of WRS and internal pressure.

propellant tank; Y-ring; residual stress; numerical simulation; welding

2016-03-18; Accepted date:2016-07-05

WU Ai-ping; Tel: +86-10-62773859; E-mail: wuaip@mail.tsinghua.edu.cn

10.19476/j.ysxb.1004.0609.2017.04.004

1004-0609(2017)-04-0701-07

V414.4

A

2016-03-18；

2016-07-05

吴爱萍，教授，博士；电话：010-62773859；E-mail: wuaip@mail.tsinghua.edu.cn