一种IAE指标触发的继电反馈PID参数自校正方法

范惠剑，王志国，刘 飞

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122 )

一种IAE指标触发的继电反馈PID参数自校正方法

范惠剑，王志国，刘 飞

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122 )

针对实际工业过程中固定PID参数不能适应系统特征变化的问题，提出了一种在线控制器参数自动校正方法;首先，以内模控制为基础，由系统工作数据估计得到设定值阶跃变化下系统可获得的最优累积绝对误差值(IAE)，并以此建立评价当前控制器优劣的性能指标;若性能不满足要求，则触发PID参数校正算法工作，通过引入继电反馈环节使控制回路振荡，获得控制系统临界信息，再根据改进的Z-N规则计算新的PID控制器参数;最后，分别用仿真和实际液位控制系统验证所提方法的有效性。

PID参数校正；性能评估；累积绝对误差；继电反馈；内模控制

0 引言

虽然各种先进控制技术的研究已取得丰硕成果，但在实际工业过程中，PID控制器仍被大量使用[1]，对其控制性能的评估和优化是研究热点之一。新实施并经过仔细调节的PID控制器一般都性能良好，但随着时间推移，工业现场的工况或控制回路中的某些环节发生改变，造成当前控制回路的性能衰减，不能达到期望的要求。由系统维护人员逐一对一个大型控制系统中的各PID 控制器进行重调是一件耗时耗力的工作。因此，在不影响原控制系统正常运行的情况下，对PID控制器的参数自动校正具有重要的实际意义。

最早涉及控制器参数校正研究的学者是Ziegler和Nichols，他们提出利用过程对象的阶跃响应数据，结合经验公式对PID控制器参数进行整定，目前大多工程师手动调节控制器参数时仍基于该思路。Astrom和Hagglund提出了使用继电反馈环节调节控制器参数的方法，通过在控制回路中引入继电器非线性模块使回路产生临界振荡，再由此时的特征数据估计出控制器参数，进而实现PID校正过程[2-3]。基于继电反馈思想，Tan提出了一种改进的PID控制器参数校正方法，在确定期望闭环频率响应模型的基础上，利用继电器环节工作时对象在临界频率下的响应特征直接整定获得最优的控制器参数[4]。Jeng提出了一种仅利用过程响应数据直接对PID控制器进行校正的方法，该方法优点是不要求过程模型为已知，但实施中需加入外部激励，这在实际应用中存在局限[5]。

控制性能评估(CPA)主要研究在不影响系统正常运行的情况下评估当前控制系统的性能，分为随机性能评估和确定性能评估。随机性能评估的主要代表是基于最小方差的性能评估方法，也是目前研究成果最丰富的领域[6-9]。随机性能评估方法侧重评价控制回路的稳态性能，对系统动态过程评价不充分。Swanda和Seborg等提出利用累积绝对误差(IAE)的大小来评价控制系统动态响应性能，这是一种确定性能评估方法[10]。Veronesi和Visioli等根据简单内模控制原理(SIMC)，获得了阶跃响应下的IAE性能指标[11-12]。再此基础上，Yu获得设定值为斜坡类型的IAE理论最小值，并对斜坡输入下控制回路确定性能进行评估[13-14]。

前述有关PID参数校正的文献单纯研究校正方法本身，其实际应用时一般要求中断控制系统的正常运行，待参数校正完成后再让系统恢复运行。本文将确定性能评估方法和继电反馈PID参数校正方法相结合，以基于IAE的性能指标在线评估控制系统的性能，如性能不满足要求，则触发继电反馈环节对控制器参数进行校正，获得新的控制器参数。文章最后分别通过仿真和实际液位控制系统对该方法的有效性进行了验证。

1 性能评估指标的确定

在图1所示的单输入单输出(SISO)控制回路中P(s)表示过程对象，C(s)表示控制器，r(t)、e(t)和y(t)分别表示设定值、误差值以及输出值。本文考虑C(s)为PID控制器的情况，其表达式为:

(1)

式中,Kp、Ti和Td分别为比例、积分和微分系数。

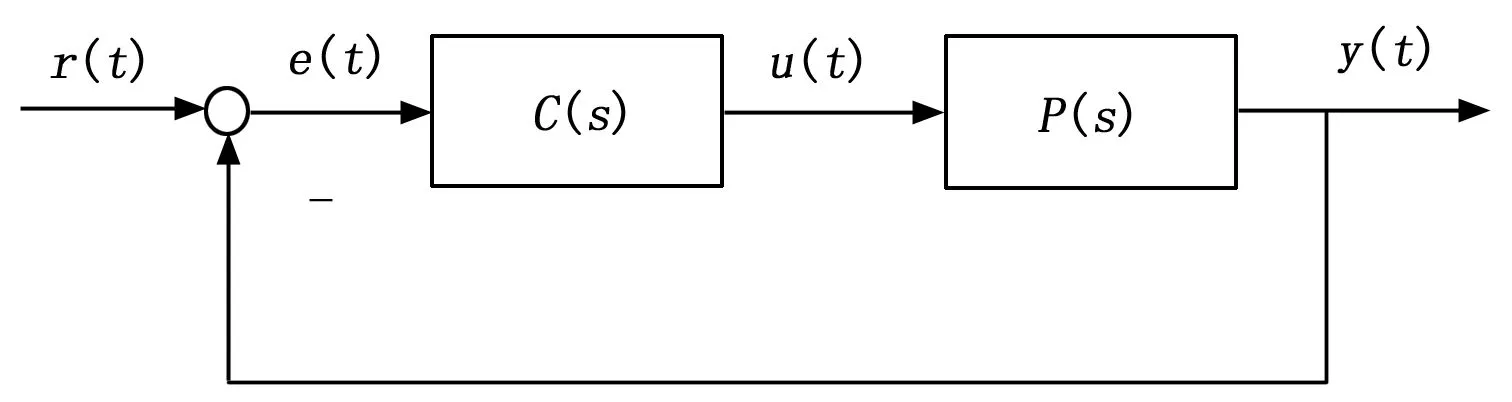
图1 单输入单输出控制系统结构图

考虑过程对象P(s)的一般性，其传递函数为:

(2)

式中,τi0为时间常数，其按照大小量级有序的排列，即(τ10≥τ20≥...)。

为获得用于评价控制器的性能指标，首先需研究最优PID控制器作用下系统能获得的最好性能。由于PID控制器和内模控制之间可以互相转换，我们可以在内模控制原理(IMC)基础上[16]，利用直接校正获得最优PID控制器的参数。

首先，使用Skogestad提出的半规则模型降阶法，过程对象可近似为二阶时滞模型[15]。

(3)

其中:

(4)

IMC目标就是在最优的控制器下，使得期望的闭环传递函数为:

(5)

则在期望的闭环传递函数下，用直接法求得最优内模控制器为:

(6)

进一步将式中e-θs通过泰勒级数展开近似为e-θs=1-θs并将其带入最优控制器中得：

(7)

将其与公式(1)的PID控制器相比较得最优控制器参数为：

(8)

式中,τc是期望的闭环时间常数。一般而言，τc应大于过程延迟θ，因为当τc<θ时控制回路的响应会过于激进甚至产生震荡。综合考虑系统响应的快速性、控制量的幅值限制以及闭环回路的鲁棒性，并根据文献[11]所述，当取τc=θ时，系统性能最为理想。此时，如果控制回路施加幅值为的阶跃信号r(t)，可得闭环阶跃响应为:

(9)

对上式进行拉普拉斯逆变换，可得:

(10)

则误差信号e(t)=r(t)-y(t)为:

(11)

根据IAE的定义，理论上最优的PID控制器作用下的IAE取值为:

(12)

为直观表示PID控制器性能的优劣，我们定义用实际绝对累积误差与理论值的比值作为性能指标CI:

(13)

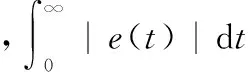
2 PID参数自校正

根据控制系统运行数据，实时估计控制性能指标CI，当性能不满足要求时，我们启动继电反馈校正算法，估计系统临界特征数据，并对控制器参数进行校正。图2为本文所提出的在线PID参数自校正方法的系统原理图，包括继电器环节、PID控制器，被控对象和性能评估(CPA)模块四部分组成。其中，性能评估模块主要作用就是上节所述的CI估计环节，利用阶跃响应下数据，在线对控制器确定性能进行评估，若性能不满足要求，触发系统切换开关，进行继电反馈PID参数自校正。

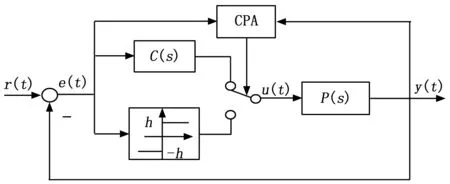
图2 PID参数校正原理图

2.1 继电反馈PID参数校正

继电反馈PID参数校正是一种基于相角裕度和幅值裕度的控制器自整定方法。其系统校正如图3所示，系统利用继电器的非线性特性产生一个如图4所示的临界振荡，然后通过描述函数法获得该振荡的临界周期和临界增益。并且整个过程在无需任何外部激励信号便可获得所需的临界信息。

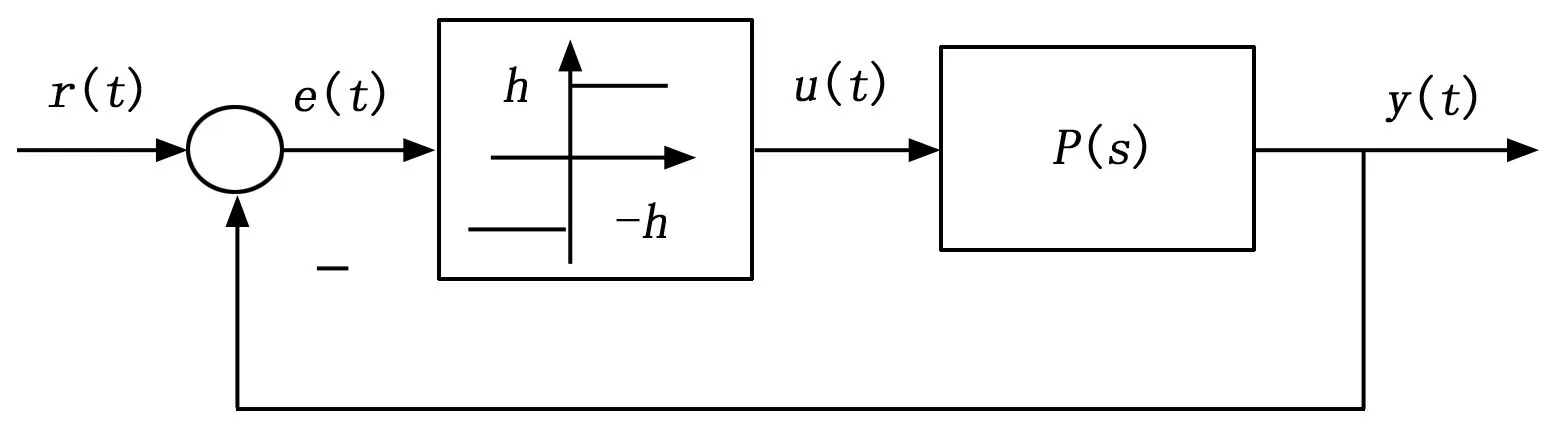
图3 继电反馈控制框图

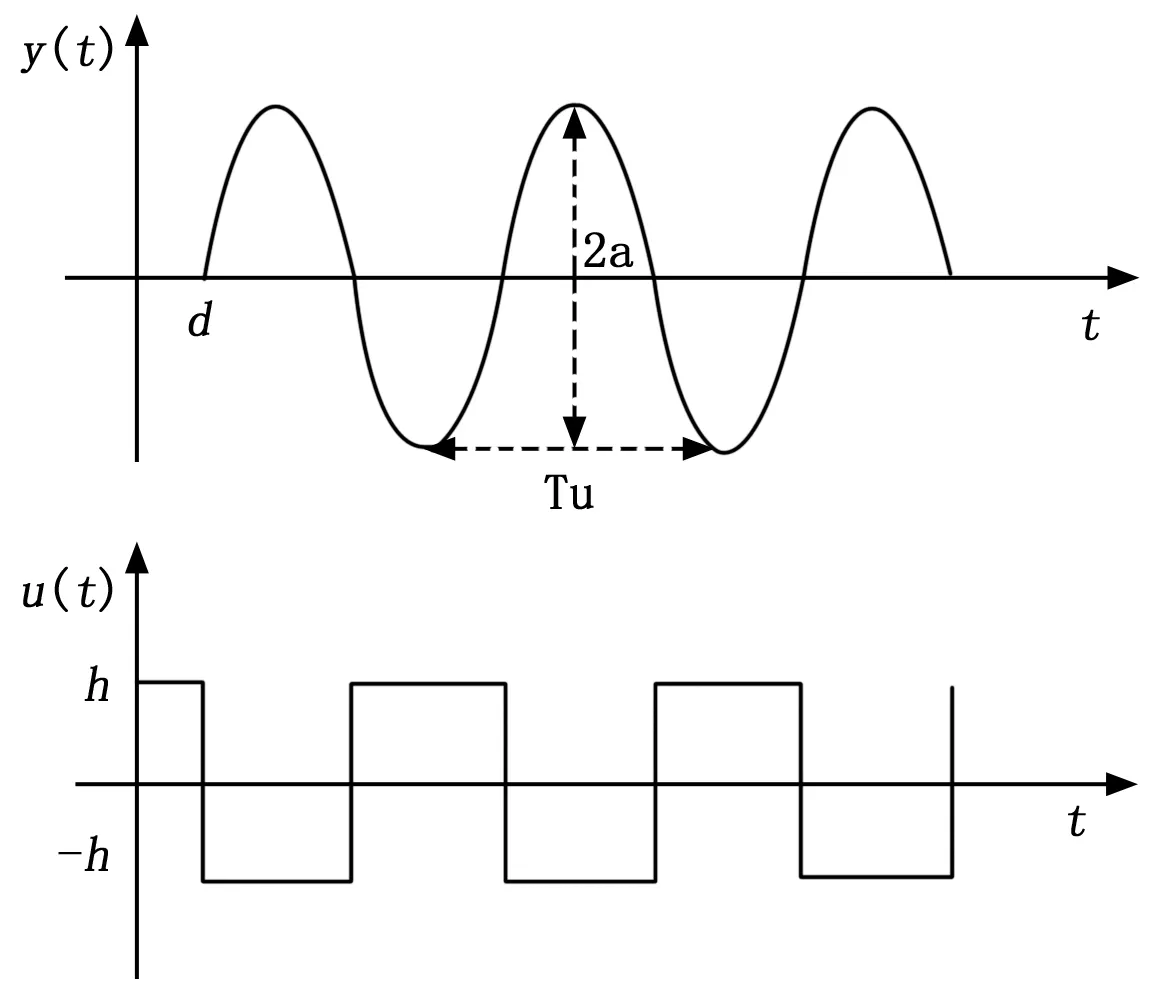
图4 继电反馈系统过程曲线

为了获得振荡过程的临界信息，通过非线性分析可知，典型的继电特性描述函数如下：

(14)

式中,h是继电环节的幅值，a为振荡曲线的幅值。当系统产生临界震荡时，由奈奎斯特稳定判据可知1+G(jωu)N(a)=0，所以临界增益和频率如下：

(15)

(16)

根据系统的振荡曲线，能够获得振荡幅值a，振荡周期Tu，从而辨识出系统的临界增益Ku和临界频率ωu。然后在获得的临界信息基础上，根据Z-N校正规则对PID控制器校正。然而传统的Z-N校正规则获得控制器参数可能会对回路产生较大的超调。尤其对设定值变化下的控制器的参数校正不能达到满意效果。为此，本文考虑使用一种改进的Z-N校正规则(即适度超调规则)，该规则在原始校正规则基础上对比例系数Kp的整定公式做了调整，使其校正后控制回路产生适度的超调。具体的校正规则如表1所示。

表1 PID控制器参数校正规则

2.2 PID参数自校正算法步骤

利用系统的运行数据，在线对控制器性能评估。当性能不佳时，立即触发开关，切换到继电校正环节对控制器进行校正。具体校正算法如下：

1)在系统正常工作状态下，采集阶跃响应下系统工作数据e(t)、y(t)；

2)估计系统的延迟时间θ，一般延迟时间选取为系统初始时刻到其2%的稳定值所需的时间间隔；

3)通过估计的延迟时间和系统的阶跃幅值计算累积绝对误差理论值IAE0；

4)根据采集的误差数据计算实际累积误差值，并根据公式(13)计算性能指标CI；

5)如果CI<0.6，则触发控制器参数自校正；

6)控制器参数自校正

(a)切换系统开关，用继电器取代回路中PID控制器；

(b)在继电器作用下，系统产生振荡，利用系统振荡数据估计出系统的临界周期和增益；

(c)根据改进的Z-N规则，计算控制器参数；

(d)校正结束后，切换系统开关，控制器正常工作；

7)结束

上述PID在线自校正算法中，在选取继电器幅值h时，既要使系统在继电器作用下产生等幅振荡，又要保证产生的振荡幅值在系统允许范围内，大量的实践经验表明一般选取继电器幅值h在(0,σy(t))区间范围内。其中σ为权系数，其值的选取由实际的控制要求决定。

3 算法仿真和实验

3.1 仿真

(17)

为了验证本文所提算法的有效性，利用上述过程对象进行仿真实验，初始化控制器参数Kp=2.00,Ti=0.56,Td=1.10。在单位阶跃输入信号下，在线采集控制回路的工作数据，估计出延迟时间θ=1.2，进一步计算出性能指标CI=0.27，系统的阶跃响应曲线为图5中[0, 800]时间区间。

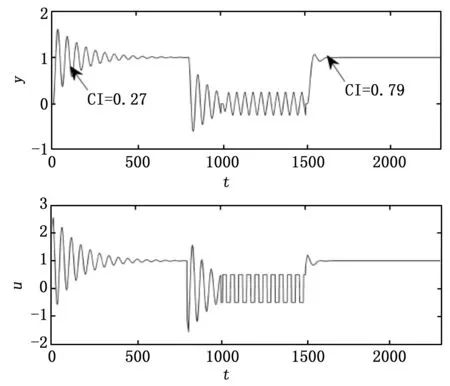
图5 过程响应曲线

由图可知，在当前PID控制器下控制回路性能较差，此时性能指标小于0.6，立即触发系统开关切换到继电器环节进行参数校正。校正过程中，设置继电器幅值d=0.5，在继电器的作用下，系统产生临界振荡，通过振荡数据获得系统的临界周期Tu=4.80，临界增益Ku=2.54，在此基础上，利用改进的Z-N规则(即适度超调校正规则)获得校正后的PID参数值为Kp=0.85，Ti=0.35，Td=0.51。当校正结束后，系统自动切换开关，并重新采集一组阶跃响应下的过程数据，并计算出性能指标CI=0.79。比较校正前后过程输出曲线可知，系统超调量、调节时间等动态性能也得到了明显改善。

3.2 液位控制实验

为验证本方法在实际工业控制中有较强的适用性，选择双容水箱液位控制的实验装置进行验证。图7为双容水箱液位控制系统。该装置由水槽、上、下水箱三部分构成一个闭环回路。本文控制目标是控制下水箱的液位高度，所以将下水箱液位作为输出，水泵的电压作为输入信号，并通过水箱底部的压力传感器来检测液位高度。设置控制器参数为Kp=3.3,Ti=0.84,Td=6.47同时通过数据采集装置以0.1s时间间隔采集工作数据。在幅值为5的阶跃输入信号下采集水箱数据估计出系统的延迟时间θ=2，并且计算出性能指标CI=0.33，系统输出曲线为图6中[0,3000]时间区间，从图中可以看出系统超调大，趋于稳定时间较长，系统性能不佳。在t=3 000时，触发系统切换开关，进行控制器校正，其中设置继电器幅值d=10，在继电器作用下系统产生临界振荡，根据振荡曲线获得过程对象的临界信息，并通过改进的Z-N校正规则得到PID参数值Kp=2.7，Ti=0.33，Td=5.44。校正结束后，切换系统开关，在相同阶跃信号下重新采集系统工作数据，一段时间后计算出性能指标CI=0.67。

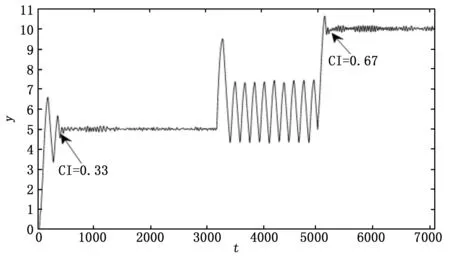
图6 液位控制过程输出曲线

图7 液位控制系统

综合比较校正前后系统性能可知，校正后的控制系统不仅性能指标得到显著提高，而且其他动态性能指标也得到相应的改善。由表2可知系统的超调量由校正前的31.8%降低到12.8%，并且系统的响应速度也变快了0.2s。

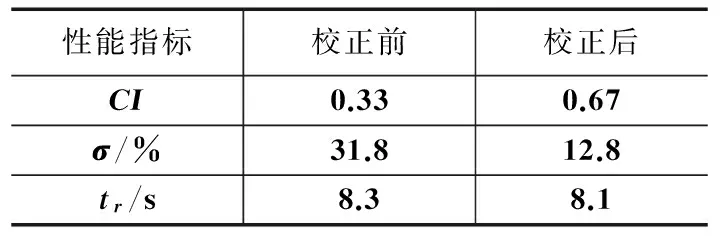
表2 液位控制校正前后性能指标

4 结论

本文针对工业过程中PID控制器，提出了一种IAE指标触发的继电反馈自校正方法。该方法无需中断系统的正常运行，且不依赖过程先验知识，仅利用系统设定值变化下的工作数据，在线对控制器进行性能评估，并以性能指标为触发条件自动校正控制器参数。通过实验可知，本文所提方法能够及时有效对控制回路进行性能评估及在线校正，对于工业生产具有重要的应用价值。

[1] 薛美盛,FeiQi, 张 毅,等. 控制回路性能评估综述[J]. 控制工程, 2009, 16(5):507-512.

[2]AstromKJ,HagglundT.PIDcontrollers:theory,designandtuning[J].InstrumentSocietyofAmerican, 1995, 34(7):46-52.

[3]AstromKJ,HagglundT.Automatictuningofsimpleregulatorswithspecificationsonphaseandamplitudemargins[J].Automatic, 1984, 20(5): 645-651.

[4]TanKK,LeeTH.Robuston-linerelayautomaticofPIDcontrolsystems[J].ISATransactions, 2000, 39: 219-232.

[5]JengJC,TsengWL,ChiuMS.Aone-steptuningmethodforPIDcontrollerswithrobustnessspecificationusingplantstep-responsedata[J].ChemicalEngineeringResearchandDesign, 2014, 92(3): 545-558.

[6]HarrisTJ.Assessmentofcontrolloopperformance[J].CanadaJournalofChemicalEngineering, 1989, 67(10): 856-861.

[7] 张 魏, 王 昕, 王振雷. 基于多模型混合最小方差控制的时变扰动控制系统性能评估[J].自动化学报, 2014, 40(9): 2037-2044.

[8] 王志国, 刘飞. 一类非线性系统的最小方差性能评估策略[J]. 控制与决策, 2012, 27(10): 1593-1596.

[9]HuangB.Apragmaticapproachtowardsassessmentofcontrolloopperformance[J].AdaptControlSignalProcess, 2003, 17(7-9): 589-608.

[10]SwandaAP,SeborgDE.Controllerperformanceassessmentbasedonsetpointresponsedata[A].AmericanControlConference[C]. 1999, 6: 3863-3867.

[11]VeronesiM,VisioliA.PerformanceassessmentandretuningofPIDcontrollers[J].Industrial&EngineeringChemistryResearch, 2009, 48(5): 2616-2623.

[12]VeronesiM,VisioliA.AnIndustrialapplicationofaperformanceassessmentandretuningtechniqueforPIcontrollers[J].IASTransactions, 2010, 49: 244-248.

[13]YuZ,WangJ,HuangB.PerformanceassessmentofPIDcontrolloopssubjecttosetpointchanges[J].JournalofProcessControl, 2011, 21(8): 1164-1171.

[14]YuZ,WangJ.Performanceassessmentforfeedforwardcontrollerssubjectedtoloaddisturbances[J].JournalofProcessControl, 2014, 53(27): 11050-11060.

[15]SkogestadS.SimpleanalyticrulesformodelreductionandPIDcontrollertuning[J].JournalofProcessControl, 2003, 13: 291-295.

[16]LeeY,LeeM,BrosilowC.PIDcontrollertuningfordesiredclosed-loopresponsesforSISOsystems[J].AIChEJournal, 1998, 44(1): 106-115.

ARelayAutomaticTuningofPIDControlSystemsTriggeredbyIAEIndex

FanHuijian,WangZhiguo,LiuFei

(MinisterialKeyLaboratoryofAdvancedProcessControlforLightIndustry,JiangnanUniversity,Wuxi214122,China)

A new on-line automatic tuning method for PID controllers is presented to solve the problem that PID parameters can not adapt to the change of system characteristics. Firstly, on basis of the internal model control (IMC), the optimal integrated absolute error (IAE) is estimated by the operating data of control system when the set values are changing. Then performance index is established to evaluate the controller. If the performance does not meet the requirements, the PID tuning algorithm is triggered. The critical information can be identified from the oscillating curve which is caused by the relay. Then, the optimized PID parameters are obtained according to the improved Z-N rules. Finally, the effectiveness of the proposed method is verified by a simulation example and an actual level control system.

PID parameter tuning; performance assessment; IAE; relay feedback; IMC

2016-11-07；

2016-11-29。

国家自然科学基金项目(NSFC61403167); 江苏省研究生培养创新工程(SJLX15_0571)。

范惠剑(1991-)，男，江苏江阴人，硕士研究生，主要从事控制器性能评估方向的研究。

1671-4598(2017)04-0066-04DOI：10.16526/j.cnki.11-4762/tp

TP

A