文化遗产数字化形状匹配方法研究

邓小盾

（西安外事学院 陕西 西安710077）

文化遗产数字化形状匹配方法研究

邓小盾

（西安外事学院 陕西 西安710077）

针对文化遗产中的壁画图像数字化处理和形状匹配问题，文中采用分数阶微积分的方法进行图像处理，同时采用分数阶微积分和尺度不变特征变换（SIFT）算法相结合的方式，提高图像匹配结果的准确度，同时本论文还对分数阶微积分阶数进行实验研究，实验研究表明：采用分数阶微积分和尺度不变特征变换（SIFT）算法可将图像匹配的准确率提高到95.83%。

文化遗产；形状匹配；分数阶微积分；SIFT

我国历史悠久，在历史长河中诞生了大量的文化遗产，尤其以壁画为主，壁画能够真实展现我国不同时期的文化，因此对壁画的保护和分析对了解我国历史具有主要的研究价值，尤其敦煌壁画，是我国和世界闻名的珍贵历史文化遗产之一[1]，因此，如何保护敦煌壁画以供世人观赏，是学者们研究的重点。计算机科学的迅速发展，为解决这些问题提供了新的方法和途径。而对于文化遗产数字化分析中的一个关键问题就是对壁画特征的提取和通过提取的特征能够匹配出原始的图像特征，因此进行壁画等文化遗产数字化形状匹配技术的研究具有重要的研究意义[2-3]。

分数阶微积分技术能够选择任意实数作为其阶数，形成了连续阶微积分，不仅能够实现整数阶微积分的功能的进一步扩展，还能进一步应用于图像分析与处理等领域[4-5]。同时尺度不变特征变换（Scale Invariant Feature Transform，SIFT）算法是一种基于局部特征的特征描述方法，也是到目前为止最有效的局部不变特征描述方法，广泛地应用于目标检测、图像识别方面[6-7]。因此结合分数阶微分方法和SIFT方法则可实现对图像的轮廓特征进行提取和匹配，这样则可有效实现不同壁画信息的数字化匹配识别。因此，文中将分数阶微积分和SIFT应用到文化遗产数字化研究当中，具有重要的研究意义。

1 理论背景

1.1 分数阶微积分理论

从对信号（图像）分析与处理的角度来说，微积分运算可以实现对信号的滤波效果，当分数阶时进行微分运算，可对该信号中的高频部分进行加强，而当时，则是对信号进行积分运算，此时则是可以加强信号的低频部分，而当时，则不对信号进行处理，因此针对信号特征选择合适的阶数则可实现对信号的降噪处理[8-9]。其中G-L是目前流行分数微积分处理方法，G-L分数阶微分定义来源于经典的整数阶次的微分，他把微积分的阶次从整数拓展到分数，即[10-11]。

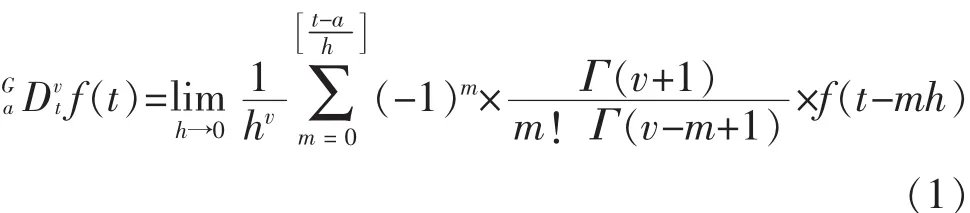
若f（t）的自变量t取值的范围为[a，t]，可以将这个区间的间隔h=1的长度进行等分处理，此时可以得到进而可以得到了该信号的分数阶的查分形式为：

此后需要在M×N的图像上使用m×n的分数阶掩模对预处理的图像进行滤波处理。如下：

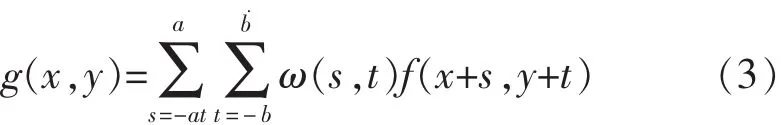
为了实现整体图像的信息全部进行处理，此时需要对x=0，1，2…M-1和y=0，1，2…N-1以此采用等式（3）在8个对称的方向上进行微分处理。其给出的差分式的前项乘数如下：

采用上式则可实现每一个方向上后市相同系数的滤波器，实现图像的滤波。

1.2 SIFT理论

SIFT（Scale Invariant Feature Transform）算法由D.GLowe 1999年提出，2004年完善总结。SIFT算法为在尺度空间寻找极值点同时提取位置的算法，也为尺度以及旋转不变量的提取局部特征的算法。SIFT算法的主要特点[12-13]：

1）SIFT算法是提取的图像的局部特征，能够对图像的旋转、尺度缩放以及亮度等的变化保持较好的不变性，在其视觉、放射以及噪声等的变化中也能够保持较好的稳定性。

2）信息量丰富多样化，且具有较好的独特性，能够在海量特征数据中快速精准的配置到相应的信息。

3）多量性，SIFT特征向量与物体数量无关，即使少数的个体也能产生多量的特征向量。

4）高速性，SIFT匹配算法在简化后能够达到实时性的要求。

5）可扩展性，该特征向量非常易于完成与其他形式特征向量间的联合。

SIFT交通标示特征形成的计算步骤详述如下：

1）尺度空间检测极值点：首先是采用高斯差分公式进行尺度和图像位置的全方位搜索，获取所有潜在的特征点，所检测的特征点能够对尺度缩放的旋转变换保持不变。

2）关键点的定位：对于每个点，确定他们的位置和尺度；

3）确定关键点的方向：每一个关键点应当匹配一个方向，对于图像数据的操作也均通过特征点方向、尺度和位置进行，以保障其不变性。

4）生成特征点描述子：通过对关键点当前尺度周围区域梯度的统计，获得特征点描述子。

2 文化遗产数字化形状匹配实验

敦煌石窟的壁画是敦煌石窟最主要的艺术表现形式。这些是具有极高艺术价值和考古价值的文物，壁画主要需要获取它的视觉信息和形状形式，文中以壁画图像为对象进行数字化匹配实验，对其首先采用G-L分数阶微分方法对其进行图像效果加强处理，之后对处理后的图像采用SIFT进行图像匹配，文中相关计算程序在MATLAB计算软件下进行。本文设计的壁画图像处理及匹配实验流程如下[14-15]：

获取敦煌典型代表壁画；

采用G-L分数阶微分方法进行壁画效果的加强处理；

设定两幅对比图像，其中一幅图像进行旋转15°；

采用SIFT方法计算图像的特征点；

对提取的图像特征点进行图像匹配；

对比不同分数阶微分下的SIFT图像匹配结果，确定最佳组合方式。

2.1 基于G-L分数阶微分的图像处理

图像增强技术是为了提高图像中信息的对比度，提高并改善图像的信息表现能力，是图像处理领域中对图像的一种基本的处理，也是对图像进行更高层次地处理与分析的基础。G-L分数阶微分定义来源于经典的整数阶次的微分，他把微积分的阶次从整数拓展到分数。即根据式（4）可以做出每个方向都是相同系数的滤波器，比如可以做出大小的八方向微分算子，采用分数阶微分运算的方法处理二维数字图像是实现一维滤波器向二维滤波器的转换，因此，图像中的每一像素点均需要进行分数阶微分运算，以保障处理了图像中的每一点。为了实现掩模算子的抗旋转性，我们选择从8个计算方向。根据式（4）构造8个方向的大小的分数阶微分掩模算子如表1所示。更大的模板里面，对于非此8个方向的数值则均可定义为零。

表1 分数阶微分算子

表1所展示的算子叫做 Tiansi微分算子，根据目标图像并考虑模板对图像处理的效果及复杂度，选择尺度大小适宜的掩模模板，例如5×5大小的分数阶微分掩模算子ω（s，t）如表2所示。

表2 5×5大小的分数阶微分掩模算子

此算子可以对图像进行处理，从而获得增强后的图像然后将上述算子Matlab平台下实现图像的增强，选取分数阶微分中较好的阶次，文中对对我国文化遗产敦煌某壁画采用5×5大小的分数阶微分处理后的其效果如图1所示，其评价指标如表3。

由表3可知，采用文中的分数阶微分方法对敦煌壁画处理结果后，大大改善了图像的增强效果，较好的提升了均值和清晰度，因此，说明本研究中改进传统的分数阶微分模板这一思路是可行的。

2.2 基于SIFT的图像匹配

图像匹配是图像处理中的一个根本的任务，其是对同一目标物体在不同时间，或不同场景，或不同视觉等不同成像条件下所得到的两幅或多幅图像进行比较分析，找到其中相同或相似部分，并标记出来。由于各种匹配算法思想的出发点和原理的不同，因此，不同的图像匹配算法的步骤也会有些区别，但是其基本过程是大同小异的。总体来说，图像匹配的流程图可归结为分别对两幅带匹配图像进行SIFT特征提取，对提取的特征建立特征向量集，建立好的好特征向量集进行SIFT特征匹配，最后确定对应点集[16]。对于SIFT计算过程而言，其关键算法为图像中的某个关键点的选择，同时比较分析与另一幅图像中表现为距离最近的前2个关键点，所获得的2个关键点，如果最近的距离除以次近的距离所得的值小于某个阈值Th，则这一对匹配点可以接收。匹配点数量可随着比例阈值的降低而逐渐增多，但稳定性则相反。在本研究中，我们选择阈值为0.8，大于此阈值则不予以接收，因此，正确匹配的丢失率仅为5%，而错误匹配却可以消除掉90%。

图1 采用分数阶微分的图像增强效果图

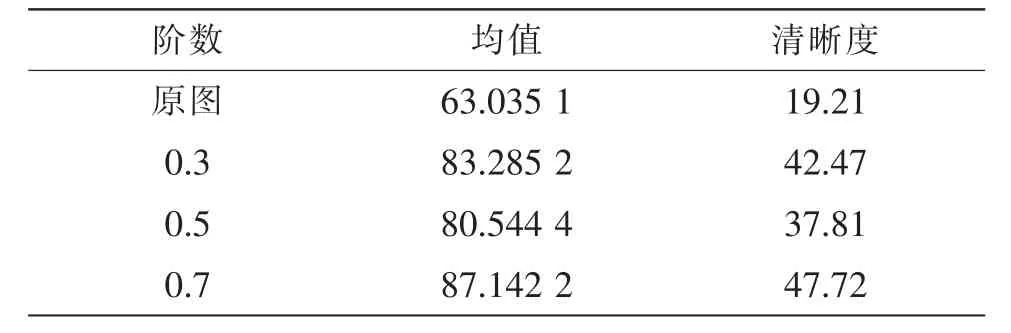
表3 图像增强评价指标

文中给出了两幅原始图像如图2所示，其中图（a）为进行灰度处理的原始图像，图（b）则是将灰度处理后的原始图像旋转15度。文中采用欧氏距离法，对于一副图中的每个特征点，在另一幅图中找到与之距离最近的特征点的距离d1和次近的特征点的距离d2，若d1/d2＜Th，则接受该匹配。图像匹配结果如图2中的有颜色的连线和关键点所示。其中有颜色的连线的两端是两幅图像中对应的匹配点。一共找到了15个成功匹配的关键点，可见其对视角变换保持一定的稳定性。由此可见，除了少数几个不能正确匹配，大部分的匹配都是成功的，因此对图像旋转变换保持一定的稳定性。

图2 基于SIFT的图像匹配结果

2.3 对比实验结果与分析

为了验证分数阶微积分能有效提高图像SIFT匹配算法的性能。需要对比不同分数阶微分进行图像后匹配效果，获取最佳图像匹配效果的组合方式。本文选取不同阶数对多幅图像采用SIFT算法对图像进行特征点提取，对提取后的特征点进行图像匹配，对比实验结果如表4所示。

通过表4可知：未采用分数阶微分算法时的原始图像（a）中的关键点为30个，图（b）中的关键点数量为24个，图像的匹配准确率仅为75%。而采用了本文介绍的分数阶微分方法后图像的清晰度加强，图像识别出的关键点数量也增加，同时图像匹配的准确率也随之增加了，如采用0.2阶的分数阶微分方法对图像亮度加强处理后，图（a）采用SIFT方法计算获得的特征关键点数为36个，比原始图像多了6个，而图（b）获得的关键点数为25个，比原始图像多了1个，同时匹配的准确率也大大提高了 （为88.89%）。为了获得最佳的匹配效果，文中将0.2阶到0.9阶计算后的图像分别进行SIFT匹配，通过结果可以看出采用0.7阶的分数微分的图像处理效果最好，其中可识别出图（a）中的39个关键点，图（b）中的30个关键点，匹配对的数量为23个，匹配错的数量仅有一个，图像匹配的准确率高达95.83%。通过实验结果表明：采用本文中分数阶微分算法和SIFT相结合的方式可提高图像匹配的真确率，且获得当分数阶取0.7阶时进行图像处理后SIFT匹配的准确率最高。

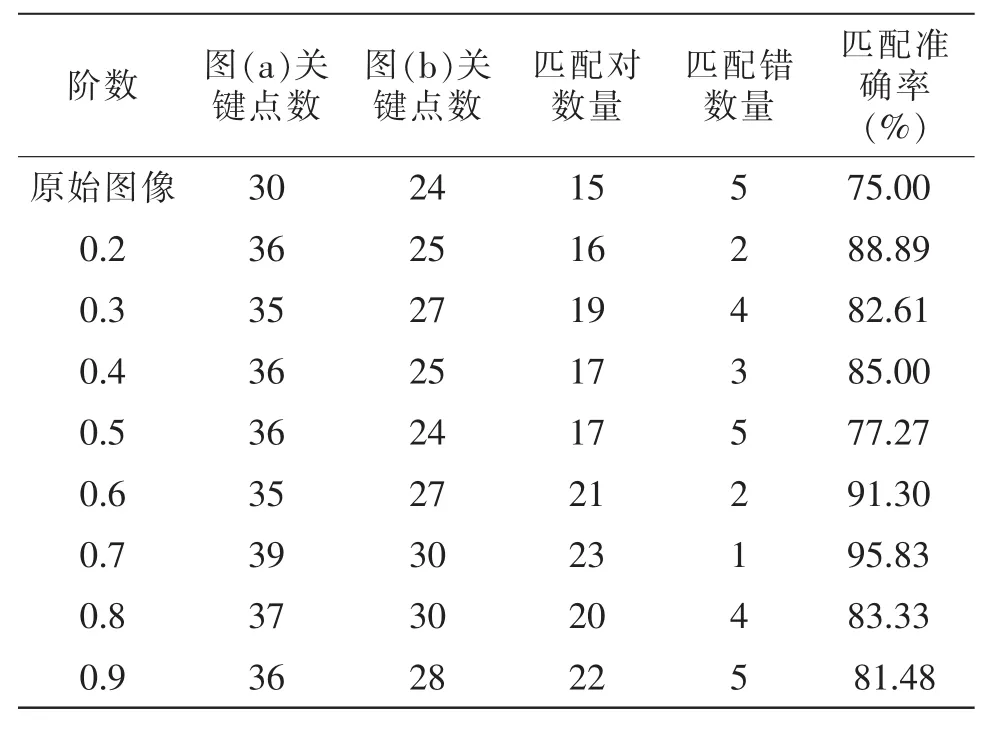
表4 不同分数阶处理后图像匹配情况

3 结 论

文中针对我国文化遗产数字化处理中的壁画图像特征的提取和通过提取的特征能够匹配出原始的图像进行研究，采用了分数阶微积分和SIFT图像匹配方法进行实验研究，实验结果表明：采用分数阶方法可对拍照模糊的壁画图像特征加强，SIFT的方法可实现壁画图像特征提取和匹配，而采用分数阶微积分算法和SIFT[17-20]相结合的方式可提高图像匹配的准确率，通过实验获得最佳分数阶微积分和SIFT组合方式为：当分数阶取0.7阶时进行图像处理后的SIFT匹配的准确率最高。文中的研究对壁画等文化遗产数字化形状匹配技术的研究具有重要的研究意义。

[1]黄永林，谈国新.中国非物质文化遗产数字化保护与开发研究[J].华中师范大学学报：人文社会科学版，2012（2）:49-55.

[2]吴品才，储蕾.非物质文化遗产档案化保护的理论基础[J].档案学通讯，2012（5）:75-77.

[3]戴其文，刘俊杰，吴玉鸣，等.基于区域视角探讨广西非物质文化遗产的保护 [J].资源科学，2013（5）:1104.

[4]黄果，许黎，蒲亦非.分数阶微积分在图像处理中的研究综述[J].计算机应用研究，2012（2）:414-420.

[5]张丽敏，周尚波.基于分数阶微分的尺度不变特征变换图像匹配算法 [J].计算机应用，2011（4）: 1019-1023.

[6]杜京义，胡益民，刘宇程.基于区域分块的SIFT图像匹配技术研究与实现 [J].光电工程，2013（8）: 52-58.

[7]李海洋，文永革，何红洲.一种改进的SIFT特征点检测方法[J].计算机应用与软件，2013（9）:147-150.

[8]黄果，许黎，蒲亦非.分数阶微积分在图像处理中的研究综述[J].计算机应用研究，2012（2）:414-420.

[9]吴光强，黄焕军，叶光湖.基于分数阶微积分的汽车空气悬架半主动控制 [J].农业机械学报，2014（7）:19-25.

[10]李文，赵慧敏.一种分数阶微积分算子的有理函数逼近方法[J].自动化学报，2011（8）:999-1005.

[11]何明明，李宁，陈蕴生，等.基于分数阶微积分岩石的动态变形行为研究 [J].岩土工程学报，2015（S1）:178-184.

[12]李新科，高潮，郭永彩，等.利用改进的SIFT算法检测桥梁拉索表面缺陷[J].武汉大学学报：信息科学版，2015（1）:71-76.

[13]王峰，尤红建，傅兴玉.应用于SAR图像配准的自适应SIFT特征均匀分布算法[J].武汉大学学报：信息科学版，2015（2）:159-163.

[14]刘金颂，张庆阳，原思聪.基于SIFT和LTP的图像匹配方法[J].西安建筑科技大学学报：自然科学版，2014（5）:762-768.

[15]张文超，吕岳，文颖，等.几何信息与SIFT特征相结合的特定人手写关键词检测 [J].智能系统学报，2014（5）:544-550.

[16]徐衍鲁，马燕，李顺宝，等.结合颜色不变量的SIFT和形状上下文图像匹配算法[J].计算机科学，2014（S2）:144-146.

[17]许晓帆，王毅，王永泉.基于自适应非极大值抑制的SIFT改进算法 [J].电子设计工程，2014（18）：180-182.

[18]闫钧华，姜惠华，孙思佳，等.基于SIFT特征视觉词汇算法的局部遮挡目标识别[J].电子设计工程，2016（19）：159-162.

[19]郭姝言，刘桥，卢进.一种改进的医学图像深度信息恢复算法[J].电子科技，2016（1）：48-50.

[20]丁伟利，李勇，王文锋，等.基于图像的对称性识别算法研究[J].电子科技，2014（10）：1-5.

【相关参考文献链接】

许晓帆，王毅，王永泉.基于自适应非极大值抑制的SIFT改进算法[J].2014，22(18)：180-182.

任成娟，基于LPP_SIFT和巴氏距离相结合的人脸识别算法[J].2015，23(2)：35-37.

吴承隆.结合RANSAC的SIFT算法在交通视频检测中的稳像技术研究[J].2015，23(8)：143-146.

李贤丽，杜成龙.分数阶超混沌系统的动力学分析及同步[J].2014，22(16)：58-60.

王冉，金繁.基于DDS技术的线性调频脉冲信号的产生[J].2014，22(16)：52-54.

卢进军，洪信根.一种实验室信号发生器的设计[J]. 2014，22(16)：65-68.

冒洋洋.基于CORDIC算法的DDS调频信号源设计[J]. 2014，22(16)：132-134.

孙健，洪明.基于小波分析的心电信号去噪算法研究[J].2014，22(17)：130-132.

卢俊宏，王英民，牛奕龙，等.复合水声信号的光纤传输技术[J].2014，22(17)：133-136.

梁韬，李富荣，王玉峰，刘晓波.DSP航姿信号模拟器硬件设计[J].2014，22(19)：111-113.

王顶，席效禹.基于选择映射SLM降低OFDM信号峰平比的改进方案[J].2014，22(24)：42-44.

曹晖晖，张友俊.基于折叠枝节加载多模谐振器的超宽带滤波器[J].2015，23(1)：123-125.

李锋，刘芬，王宝忠.基于模糊PI控制的开关磁阻电机调速系统的MATLAB仿真[J].2015，23(8)：114-117.陈北莉.基于视觉信息的移动机器人控制系统设计[J].2015，23(3)：63-65.

凌云志，李伟光，曾顺星，等.基于EtherCAT总线的视觉目标跟踪平台设计[J].2015，23(9)：22-25.

郭海双，梁佳雯，张劭昀.MATLAB遗传算法工具箱GADS优化及应用[J].2015，23(10)：27-29.

Research on the method of shape matching in cultural digital heritage

DENG Xiao-dun
（Xi’an International University，Xi’an 710077，China）

To solve the problem of digital processing and shape matching of the mural images in the cultural heritage，in this paper，the method of fractional calculus is used for image processing.At the same time，fractional calculus and scale invariant feature transform（SIFT）algorithm is used to improve the accuracy of image matching results.In this paper，we also have the experimental study on fractional order calculus，experimental results show that the accuracy of image matching can be improved by using fractional calculus and scale invariant feature transform（SIFT）algorithm.

cultural heritage；shape matching；fractional calculus；SIFT

TP393

：A

：1674－6236（2017）01-0155-05

2015-11-30稿件编号：201511292

2016年陕西省教育厅项目（16JK2178）

邓小盾（1979—），女，陕西泾阳人，硕士，讲师。研究方向：计算机网络，人工智能。