基于更新网页排名算法的研究

高 臣，高斐斐，张家健

（1.河海大学 商学院，江苏 南京 210000；2.中国科学院 力学研究所，北京 100190；3.江苏省邮电规划设计院有限公司 江苏南京210000）

基于更新网页排名算法的研究

高 臣1，高斐斐2，张家健3

（1.河海大学 商学院，江苏 南京 210000；2.中国科学院 力学研究所，北京 100190；3.江苏省邮电规划设计院有限公司 江苏南京210000）

页面内容的内容评分与PageRank评分都需要频繁更新，以保证提供最新的结果。基于如何使得更新PageRank向量过程更为容易，并使得更为频繁的更新成为可能这一问题，本文通过对更新算法的数学内容分析，研究更新PageRank向量的问题，通过提出假设矩阵Qm×m的PageRank向量φT=（φ1，φ2，…，φm），文中立足于通过3种聚合更新算法来利用φT中的值计算G的更新后的πT，文中分析了近似聚合更新、精确聚合更新、迭代聚合更新的算法，并对3种更新算法各自的使用条件进行分析。

PageRank；近似聚合更新；精确聚合更新；迭代聚合更新

网页变化可以是网页内容的改变或是页面出链的改变，研究表明，一半以上的网页在一周内发生了变化，而近三分之一的.com网页每天都在发生变化[1]。相比于较小的网页，大型网页中的变化则更为频繁[2]。对于新增的网页，内容和链接的更新可能发生在以小时计算的时间尺度上[3]。因此，反映页面内容的内容评分与PageRank评分都需要频繁更新，以保证提供最新的结果。如何使得更新过程更为容易，得到研究者越来越多的重视。

PageRank向量可能发生两类更新：1）当超链接被加入到万维网中或从万维网中被删除时，超链接矩阵H的元素发生改变，而矩阵的大小未变。该类只有这一类型的更新，那么更新PageRank向量的问题就是链接更新问题；2）网页本身可能被加入到万维网中或从万维网中被删除，那么对于页面更新问题而言，发生的状态将被加入到马尔科夫链中或者从链中被删除，此时矩阵大小也会发生改变，此类型更新问题也更加复杂。将早期精确更新的理论结果用于PageRank问题[4]，计算结果对链接更新问题给出了理论上的答案，对于仅有一两行发生改变而且没有页面被加入或删除的情况而言，已知的精确链接更新公式是有用的，但是从计算角度分析，由于万维网的动态性，该方法对更为一般的更新而言实际价值较小[5-6]。由旧的PageRank向量开始重启幂法对于链接更新问题而言作用也较小[7]，因为不能简单地对幂法进行调整以处理更加复杂的页面更新问题，因此仅靠幂法本身来由旧的PageRank向量重启算法实际价值也较小。

1 近似聚合更新

状态聚合作为近似聚合技术方法的一部分，可以用作估计近解耦链的稳态分布。同理，可以利用一个机遇状态聚合的近似方法估计PageRank[8-9]。虽然近似聚合只能给出πk的估计值，但是近似聚合的计算量小并且可以同时处理链接更新和页面更新。利用已知分布（φT=（φ1，φ2，…，φm））以及G中的更新后的转移概率构建一个聚合马尔可夫链，其转移概率矩阵C比G更小，利用C的稳态分布ξT估计更新分布πT，具体算法包括：

将更新的马尔可夫链链的状态空间S划分为两组，即S=L∪L，其中，补集L包括所有其他状态，L是由稳态概率可能受更新影响最大的状态构成的子集，如果新加入的状态被自动包含在L中，则将受影响的转移概率设为0以处理删除的状态。需要注意，如果一个扰动只涉及PageRank大的稀疏链中的少数状态，那么它对于稳态向量的影响将主要是局部性的，因此，大多数稳态概率不会受到显著影响。根据S=L∪L导出更新后的转移矩阵及其对应的稳态分布的一个划分：

该式中G11，的大小为l×l，l=|L|为I的势，G22的大小为（n-l）×（n-l），原有分布φT中对应于L中的状态的稳态概率被存入一个行向量ωT中，而L中的状态被聚合为一个超级状态，进而得出一个更小的聚合马尔可夫链，其转移矩阵大小为（l+1）×（l+1），给出式子（e是全1列），进而利用近似程序计算出的稳态分布利用中的前I个元素以及ωT中的元素，得出产生精确的更新分布πT的一个近似，该近似值为由此可知，与获得完整的更新PageRank向量πT的精确值，该方法使用一个较小的稳态向量以构建πT的近似。

马尔科夫链可能会表现出对微小扰动的敏感性，对于扰动对马尔可夫链的影响，目前可以衡量稳态概率对于转移概率中变化的敏感程度的度量包括：转移矩阵次主特征的绝对值接近于1的程度、不同种类条件数的微小程度、平均首达时间的微小程度等。结合上述近似聚合更新的算法，需要适当地构造出划分S=L∪，并保证δT的量级处于较小规模，那么将接近于C，因此其各自的稳态分布和ξT也会相互接近，进而保证对于i≤l，i相πi互接近。如果C所定义的链在以上任何一个度量下都是良态的，那么ξT对于微小扰动将相对不敏感，即S=L∪L的恰当程度能够更加直接地体现i≤l，i≈πi的程度，因此计算的关键在于确定的良态程度。

2 精确聚合更新

对于一个不可约的n状态马尔可夫链，假设其状态空间已被划分为k个互不相交的部分S=L1∪L2∪…∪Lk，同时假设与之对应的转移概率矩阵具有分块矩阵的形式：

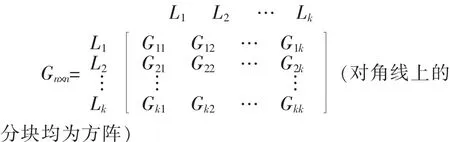
该条由G所定义的父马尔可夫链可诱导出k条更短的马尔可夫链[10]，具体的诱导方法为：与Li这组状态相对应的受限马尔可夫链定义为一个马尔可夫过程，仅当父链对Li中的状态进行访问时，该过程才会记录父链的位置，并忽略所有对Li之外的状态的访问。已知第i条受限链的转移概率矩阵为第i个随机补，由给出，其中，Gi*和G*i分别为Gii被移除后的第i行和第i列的分块，通过去除第i行和第i列的分块可得出G*i为G的主子矩阵。

为了获得较小的k状态聚合链，可以将每个组Li压缩为一个单一的状态，将父转移矩阵G压缩为聚合转移矩阵]（该矩阵为随机且不可约）

对于正则链，在由C所定义的聚合链中的状态转移，对应当未聚合的父链达到平衡时，在父链中的Li组之间的转移，其中，允许父链被分解为k个小的受限链且可以独立求解，由此解得的受限分布STi可以通过C的稳态分布加以组合构造出父链的稳态分布 πT。

对于计算πT而言，其数值求解过程并非高效，原因在于要获得受限分布STi需要计算随机补，但是随机补Si=Gii+Gi*（I-G*i）-1G*i中包含了计算成本较高的求逆运算。解决这一问题可以对受限分布进行一定程度的近似，具体包括：1）估计出随机补Si，计算这些估计的分布以得到近似设限分布，得到近似聚合转移矩阵，利用精确聚合定理计算πT的近似值；2）忽略随机补，直接对设限分布STi进行估计。

3 迭代聚合更新

迭代聚合是一种求解近解耦马尔可夫链的算法[11-12]，假设某个不可约马尔科夫链C的稳态分布φT=（φ1，φ2，…，φm），对C进行更新，令更新后的链的转移概率矩阵和稳态分布分别为G和πT=（π1，π2，…，πn），其中，更新后的G不可约，并且由于更新过程可能会新增或删除状态以及改变转移概率，m不一定等于n。具体算法包括：将更新后的链的状态划分为S= L∪，对G进行重排：

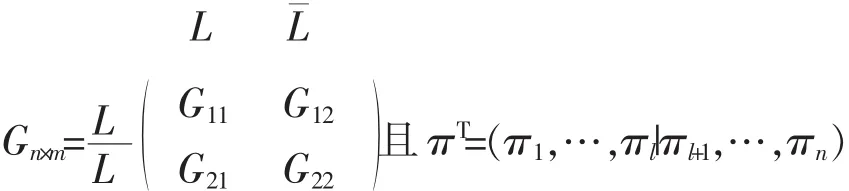
ωT对应于L状态的φT中的元素，给出式子C=进而利用近似程序计算出C的稳态分布进而得出最后令以将循环移出不动点χT。

迭代聚合更新的优点为：当使用一个良好的L-集是，相比于幂法，迭代聚合算法可以带来明显的改善，时间成本有效减少，并且随着数据集规模的扩大而越明显[13-14]。其次，迭代聚合被用于更新方法时，在更新使得问题规模发生改变的同时不会带来不利后果，因此，迭代聚合算法可以用于同时处理链接和页面更新两类更新的算法。迭代聚合更新的缺点为：首先，迭代聚合更新并不是一种普遍用途的方法，对于并非近解耦的链，迭代聚合更新一般不能获得良好的运行效果[15]。其次，向量χT是一个不动点，如果直接利用χT重启算法，在后续的迭代中将在该计算环节复制出相同的χT。最后，迭代聚合算法的收敛率直接依赖于主随机补S=G22+G21（I-G11）-1G12，收敛率完全由S最大的次主特征值所决定。相比于幂法，迭代聚合算法的每次迭代都需要进行更多的计算。

4 结 论

更新PageRank向量的研究已经展现其有效性，研究方法和思路更加追求创新和效率，但是无论近似聚合更新、精确聚合更新、迭代聚合更新，目前的研究都还不尽完善。由于不同算法给出的矩阵彼此之间存在明显差别，因此未来的研究工作可以将多个相互独立的算法的结果加以融合。

[1]Junghoo Cho，Hector Garcia-Molina.The evolution of the Web and implications for an incremental crawler[C]//In Pro-ceedings of the Twenty-sixth International Conference on Very Large Databases，New York，2000：198-210.

[2]Dennis Fetterly，Mark Manasse.A large-scale study of the evolution of web pages[C]//In The Twelfth International World Wide Web Conference，2003.

[3]Konstantin Avrachenkov and Nelly Litvak[R].The effect of new links on Google PageRank.Technical report，INRIA，2014.

[4]Meyer C D，Shoaf J M.Updating finite Markov chains by using techniquesofgroup matrix inversion [J].Journal of Sta-tistical Computation and Simulation，1980：161-179.

[5]Cho G E，Meyer C D.Comparison of perturbation bounds for the stationary distribution of a Markov chain [J].Linear Algebra and Its Applications，2010：135-155.

[6]Eugene Seneta.Sensivity analysis， ergodicity coefficients and rank-one updates for finite Markov chains [J].In William J.Stewart， Editor，Numerical Solution of Markov chains，1991：121-130.

[7]Meyer C D.Matrix Analysis and Applied Linear Algebra[M].SIAM，Philadelphia，2009.

[8]Steve Chien，Cynthia Dwork.Towards exploiting link evolu-tion[M].In Workshop on Algorithms and Models for the Web Graph，2001.

[9]James H.Aggregation of variables in dynamic systems[J].Infor-mation Processing and Management，2013：111-139.

[10]Meyer C D.Stochastic complementation，uncoupling Markov chains and the theory of nearly reducible systems[J].SIAM Review，1989：240-270.

[11]Stewart W J.Introduction to the Numerical of Markov Chains[M].Princeton University Press， 2004.

[12]杨博，陈贺昌，朱冠宇，等.基于超链接多样性分析的新型网页排名算法 [J].计算机学报，2014（4）：833-847.

[13]Sergey Brin，Lawrence Page.The anatomy of a large-scale hypertextual Web search engine[J]. Computer Networks and ISDN Systems，1998（33）: 105-118.

[14]Ayman Farahat， Thomas Lofaro. Authority rankingsfrom HITS， PageRank， and SALSA: Existence，uniqueness，and effect of initialization [J].SIAM Journal on Scientific Com-puting，2006（27）:1181-1213.

[15]Matthew Richardson，Petro Domingos.The intelligent surfer:Probabilistic combination of link and content inform-ation in PageRank[J].Advances in Neural Information Proc-essing Systems，2002（14）: 1398-1406.

Research on updating PageRank vector

GAO Chen1，GAO Fei-fei2，ZHANG Jia-jian3
（1.Business School of Hohai University，Nanjing 210000，China；2.Institute of Mechanics，Chinese Academy of Sciences，Beijing 100190，China；3.Jiangsu Posts&Telecommunication Planning and Designing Institute Co.Ltd，Nanjing 210000，China）

The score of the page content and the PageRank will require frequent updates，to provide the latest results.How to make it easier to update the PageRank vector in order to make it possible to update more frequently In this paper，the problem of updating the PageRank vector is studied through the analysis of the mathematical content of the update algorithm.Based on the PageRank vector of the hypothesis matrix（Qm×m），we propose a new algorithm based on the three algorithms（φT=（φ1，φ2，…，φm））.Based on the three polymerization update algorithm，we use φTvalue in calculation of G into πT，this paper analyzes the approximate polymerization update，precise polymerization update，iterative aggregation update algorithm，and carries on the analysis to the three update algorithm respective application conditions.

pageRank；approximate polymerization update；precise polymerization update；iterative aggregation update

TN0

：A

：1674－6236（2017）01-0006-03

2016-03-29稿件编号：201603379

江苏省社科联研究基金（201035）

高 臣（1991—），男，山东泰安人，硕士。研究方向：企业管理、技术经济。