Space-Time Correlation Based Fast Regional Spectrum Sensing in Cognitive Radio

Key Laboratory of Universal Wireless Communications Ministry of Education Wireless Technology Innovation Institute (WTI), Beijing University of Posts and Telecommunications, Beijing 100876, China

I. INTRODUCTION

With the growing development of wireless communication, the need for spectrum resource is becoming increasingly urgent. However there are no more vacant bands for allocation below 3 GHz according to the frequency allocation chart of federal communications commission (FCC) [1]. Therefore cognitive radio (CR) becomes an attractive solution since it can dynamically detect spectrum holes and access without interfering authorized services[2-3]. As its favorable propagation characteristics and low utilization, TV band is considered most suitable for CR deployment. Moreover,geolocation database is a promising solution to deploy the CR, as it records the available frequencies, related maximum transmission powers and locations and guides white space devices (WSD) which spectrum band to use,where and when to access the spectrum and when to evacuate the current band [4-5].

As a method to detect the presence of primary user (PU) and examine the spectrum band, regional spectrum sensing (RSS) plays a significant role in establishing and operating the geolocation database. The real-time channel states in the spatial domain provided by RSS contribute to make dynamic spectrum access decisions without interfering PUs. In practice, sensors move around to sense the band in the potential areas one by one to get an overview of the spatial distribution of PUs [6]. The problem of this traditional RSS method stems from its huge time and energy consumption. It is obvious that the high time delay results in little time for data transmission and unreliable sensing result. Therefore,the authorized service may be interfered and spectrum efficiency degrades.

In this paper the authors proposed a novel RSS scheme in which states of some meshes are estimated rather than all detected directly to reduce energy consumption and time delay.

Spectrum predication is widely discussed as the way to tackle the RSS problems by estimating the mesh states rather than detecting directly [7]. With spectrum predication, the number of measured locations can be reduced.For instance, there is no need to sense the places under a heavy building blockage or shadowing. In spectrum predication, the estimation of the channel states is a core problem.Existing researches put their attention to the data mining and machine learning techniques.Frequent pattern mining is adopted in [8] and[9] to estimate the current channel states, while no matter how many dimensions the original data has, the objective model is subjected to one dimension. Tumuluruet al.in [10] and[11] propose a multilayer perceptron neural network based spectrum predication model,but the training process increases the computational complexity. Xinget al.in [12] derive the probability distribution of current states conditioned on history data, and then utilize the inferred posterior to estimate the observed data, but the more computational power for result is necessary. In [13], an autoregressive model is introduced to estimate the spectrum occupancy. However, it only operates well in the additive white Gaussian noise and the lack of comparison with existing methods, which may result in the less convincing of the result.

On the other hand, the Markov process is widely used to model the dependence between the historical data and current state [14-16].A first order Markov model is proposed in[14] to predicate the channel states. Chenet al.in [15] propose a predication scheme using higher-order hidden Markov model to reduce the latency. In [16], a semi-Markov process is proposed to model the occupancy periods for each state arbitrarily. Note that the aforementioned work is based on the dependence of current and historical channel states. Since Yin verifies the existence of correlation among channels in different positions [17-18], this spatial correlation could be utilized to improve the sensing accuracy. Moreover, few predication models are tested with measurement data,which makes the results less convincing.

In this paper, we utilize the spatial channel correlation (space correlation) and historical dependence (time correlation) to improve the accuracy of spectrum sensing. To reduce the consumption of RSS, MCM clustering algorithm is proposed to classify the divided meshes into highly correlated groups. In each group, few meshes (DMs) are detected directly, while the others (EMs) are estimated by the spatial correlation according to DMs. On the other hand, the states of EMs can be obtained by the dependence on their past states modeled by Markov process using MAP principle.Moreover, as the contradictory results may be conducted by these two estimation processes,minimum entropy principle is adopted to determine the final decision. Besides, since the number of DMs in each group can be adjusted to balance the tradeoff between accuracy and consumption, the tradeoff between predication accuracy and efficiency is also explored.

To evaluate the performance of our proposed scheme, a radio environment mapping(REM) is conducted for a 500530 meters area in the downtown Beijing to collect measurement data. Measurement is conducted at a number of sampling points and signal strength of the entire area is recovered using interpolation [19]. Since symmetric sampling [20] often places sample points in inaccessible regions,a novel sampling algorithm named electron repulsion based spatial sampling (ERSS) is proposed.

The remainder of the paper is organized as follows. Section II introduces the proposed RSS scheme. The mesh clustering and mesh states estimating methods are presented in Section III. Section IV presents the REM measurement and then the spectrum usage pattern is analyzed. Performance analysis using measurement data is discussed in Section V, and Section VI concludes the paper.

II. REGIONAL SPECTRUM SENSING SCHEME

For a regional CR network, the target region is usually divided into small meshes. To get an overview of the spectrum occupancy in the whole region, there are two ways to deploy the sensors used as spectrum sensing entities traditionally as illustrated in Figure 1(a). One solution assumes that one sensor is placed in one mesh named one sensor one mesh scheme(OSOM). In OSOM, a large number of sensors are needed for a comprehensive sensing, the tremendous cost of sensor deployment should be considered. The other scheme considers that one sensor senses the divided meshes one by one. Since a sensor can only detect the channel state over one mesh at a given time,this sensing process is hysteretic and time, energy consuming, which seriously drags down the efficiency of dynamic spectrum access in the whole region. Spectrum predication is a promising solution to overcome the problems in which states of some meshes can be estimated using regional channel usage pattern such as spatial mesh correlation rather than detecting directly.

The correlation based RSS scheme in this paper is illustrated in Figure 1(b). Since spatial channel correlations exist among different meshes [18], meshes are firstly classified into highly related groups, i.e., different clustered groups are marked by different colors, and some meshes with higher correlation with others are selected as DMs, then the rest ones are estimated according to the channel states of DMs in the same group. On the other hand, as the autocorrelation over time supports of estimating current mesh state, we utilize Markov process to model this historical dependence and estimate the current states of EMs. Since spatial correlation based method and Markov based approach are independent, the contradictory results may be provided. Therefore, a minimum entropy based merging algorithm is proposed to make the final decision. The flowchart of the RSS scheme is shown in Figure 2.

III. SPACE-TIME CORRELATION BASED PREDICATION ALGORITHM

In this section, we define the mesh correlation factor to describe the mesh correlation. Then the clustering algorithm named MCM is proposed and analyzed. Two estimation methods are conducted to predicate the mesh states and a merging algorithm is introduced to determine the final result.

3.1 Mesh correlation factor

To characterize the mesh states, the spectrum occupancy information is widely represented by binary number, namely, 0 and 1. 0 presents the idle spectrum state and 1 indicates the state is occupied, the states ofith mesh atmth time slot is defined asThen the correlation between two meshes quantized by mesh correlation factor (MCF)is given by

Fig. 1 Comparison between traditional and proposed sensing schemes

Fig. 2 The diagram of proposed scheme

whereMis the number of time slots anddenotes the XOR operation. The MCF describes the dependence of channel states of different meshes, the more correlated the mesh states are, the closer theapproaches to 1, and the better we can predicate the mesh state.

In spectrum predication, we need to cluster the meshes into highly correlated groups based on MCF. However, MCF doesn’t consider the negative correlation of the meshes, since the negative correlation such asand the strong correlation indicated byare of equal importance, the MCF used previously underestimates the mesh states. To overcome this disadvantage, entropy is introduced as the metric for representing the mesh correlation.As shown in Figure 3, entropy well deals with the problem of MCF when considers the negative correlations. Moreover, since entropy quantifies the uncertainty of a random variable in information theory [21], the introduced uncertainty derived from the EMs’ states estimation according to their correlations with DMs can be described as follows.

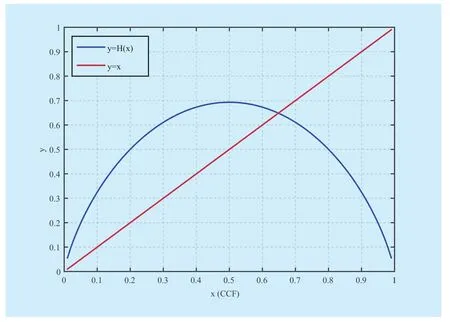
Fig. 3 Entropy versus MCF

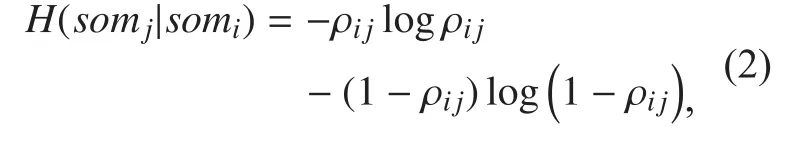
3.2 Multi-center mesh clustering algorithm

Since we utilize entropy as metric, the MCM clustering approach is presented as follows.Initially, all potential meshes are randomly classified intoIgroups,then each group selectsfixedNmeshes as DMs,is the set of DMs in groupandis thenth DM in setThe rest EMs,are estimated by DMs in the same group, the estimation probability isand the entropy of group (EP) can be calculated as

To minimize the predication error, the uncertainty introduced by estimation, which is based on spatial channel correlation between EMs and DMs, should be minimized as follows.

which means that the final DMs of this group should be chosen to minimize the EP (MEP).

Since the meshes in different groups may have strong spatial correlations, merging this kind of groups into a larger group is a reasonable choice. Thus, the sensing consumption further decreases. However, it is no doubt that decreasing the number of DMs causes the increase of the estimation uncertainty. The increment of EP is given by

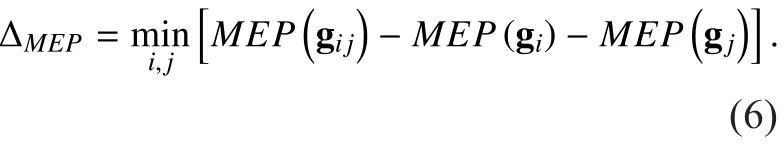
As iteration goes on, the number of DMs is reduced with the increased MEP. It is straight forward that a tradeoff exists between consumption controlled by the total number of DMs and the predication accuracy affected by the estimation uncertainty.

After we select the DMs in each clustered group, the estimation probability matrix between EMs and DMs can be found as follows.

3.3 Markov process based estimation

Since the states of TV channels have strong autocorrelation over time, the historical information can be well utilized to estimate the current states. Markov process is usually used to model this temporal dependence, which is given by whereVdenotes the order the Markov process. The transition matrix describes the dependence of historical states, and the states of EMs can be estimated using this transition matrix by the MAP principle as follows.

Algorithm 1 Multi-center Mesh Clustering Algorithm

3.4 Minimum entropy fusion method

Since these two independent estimation methods based on spatial correlation and autocorrelation over time respectively may provide the contradictory results. A minimum entropy merging approach is proposed to determine the final mesh state, which is given by

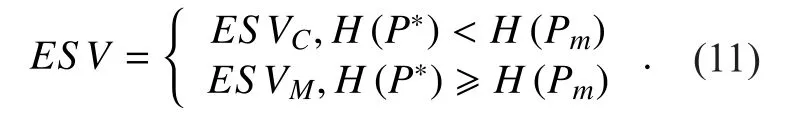
With this merging method, the space-time correlation， which combines the spatial correlation and historical dependence, is utilized to obtain a higher sensing accuracy.

IV. REM MEASUREMENT AND DATA ANALYSIS

To verify the performance of our proposed RSS scheme, spatial spectrum measurements named REM is taken in downtown Beijing,and the usage pattern of spatial measurement data is analyzed in this section.

4.1 Measurement setting

The measurement is conducted in a university beside the3rdring of Beijing, the coordinate of the measured region is (116.3483°E,39.967108°N). The shape of the area is approximately like a rectangle, which covers500meters long and530meters wide area. The region is a typical downtown in Beijing, as multiple types of landscapes are considered. As illustrated in Figure 4, the gray blocks refer to the dense residential area or teaching buildings in the north, and the wide open area is marked by green in the south.

In China, the470-806MHz spectrum band is allocated for terrestrial TV broadcasting,each TV service is loaded over8MHz channel[22]. Since the measurement has to be conducted at every preselected sampling point,only the band (550-558 MHz) carried by channel12is measured for simplicity. Moreover,note that channel12is continually transmitting the DTV broadcasting services.

Fig. 4 The distribution of sampling points in REM

Measurement equipment consists of an Anritsu MS2720T handheld spectrum analyzer on the boundaries of inaccessible areas, the Coulombic forceon theith electron placed atis given by which contains a global positioning system(GPS) module to ensure that the measurement is conducted at the preselected positions, an omnidirectional broadband antenna named BOGER DA753G kept three meters above the ground. A cable is utilized to connect the antenna and Anritsu MS2720T. Moreover, the resolution bandwidth of the spectrum analyzer is set as200kHz, and the signal strength is measured400times to avoid the influence of fluctuations. In addition, we use a200Giga-Byte hard disk inside the spectrum analyzer to store the measured data.

4.2 REM measurement

The REM measurement is divided into three steps, namely, sampling point selection, signal strength measurement and spatial interpolation[19]. Generally speaking, the commonly used spatial sampling method named symmetric sampling selects the sampling points followed by a uniform distribution [20], which is desirable in wide open areas. However, traditional symmetric sampling often places the sampling points in inaccessible areas in downtown.For example, the yellow dots selected by the symmetric sampling are unwillingly placed inside the building as illustrated in Figure 4.Although substituting the nearest accessible point for the inaccessible spot, which may result the uneven distribution of the sampling locations, is a solution, but the accuracy of the REM could be affected. On these bases, a spatial sampling named ERSS is introduced.

In ERSS, the sampling points and the boundaries of inaccessible areas are viewed as physical electrons, the repulsive force named Coulombic force pushes each electron to reach the uniform distribution and keep the sampling points out of the buildings. Assume thatNfree electrons are randomly placed in the measured region andMelectrons are placed uniformly

Since a local optimal distribution may be performed, simulated annealing [23] is usually utilized to find out the optimal result. The target function is given by

In Figure 4, the red dots stand for the sampling points generated by ERSS, and it is illustrated that all sampling points are located outside the buildings and still approximate the uniform distribution. Note that it takes us five minutes to generate the 64 sampling points in this scenario, indicating the large complexity of ERSS. However, as we can previously calculate the positions of sampling points, the complexity of ERSS is not the major concern in this paper.

With recorded signal strength at preselect sampling points, we utilize Kriging interpolation [24] to estimate the radio environment of the entire region. In addition, another100randomly selected positions, namely, verification points is measured to verify the accuracy of the measurement. The relative mean error(RME) and root mean square error (RMSE)are adopted as the performance metrics, which are defined as follows.

Figure 5 and Figure 6 show the REM of our selected area using ERSS and symmetric sampling methods respectively. It can be observed that Figure 6 has many peaks suggesting the instability of the estimation, while Figure 5 performs smoothly. The contour lines imply that ERSS clearly describes the distribution of signal strength in the entire region while symmetric sampling only illustrates roughly.Moreover, the higher region in the southeast corner refers to a playground, where experiences the maximum strength of the TV signal.While the minimum signal power (approximately -95 dBm) comes from the northern part that many tall buildings locate. To obtain an overview of power readings in this region, we utilize a uniform grid to sample 10000 points from the area and plot the probability distribution of signal strength in Figure 7. It is shown that the signal strength fluctuates between -95 dBm and -60 dBm.

4.3 Mining spectrum usage pattern

To mining the spectrum usage pattern, we need to convert the recorded power readings to mesh state vectors. Threshold comparison is widely adopted to accomplish this task,and the state of each mesh is given as follows by setting3dB above the noise floor as the threshold [18].

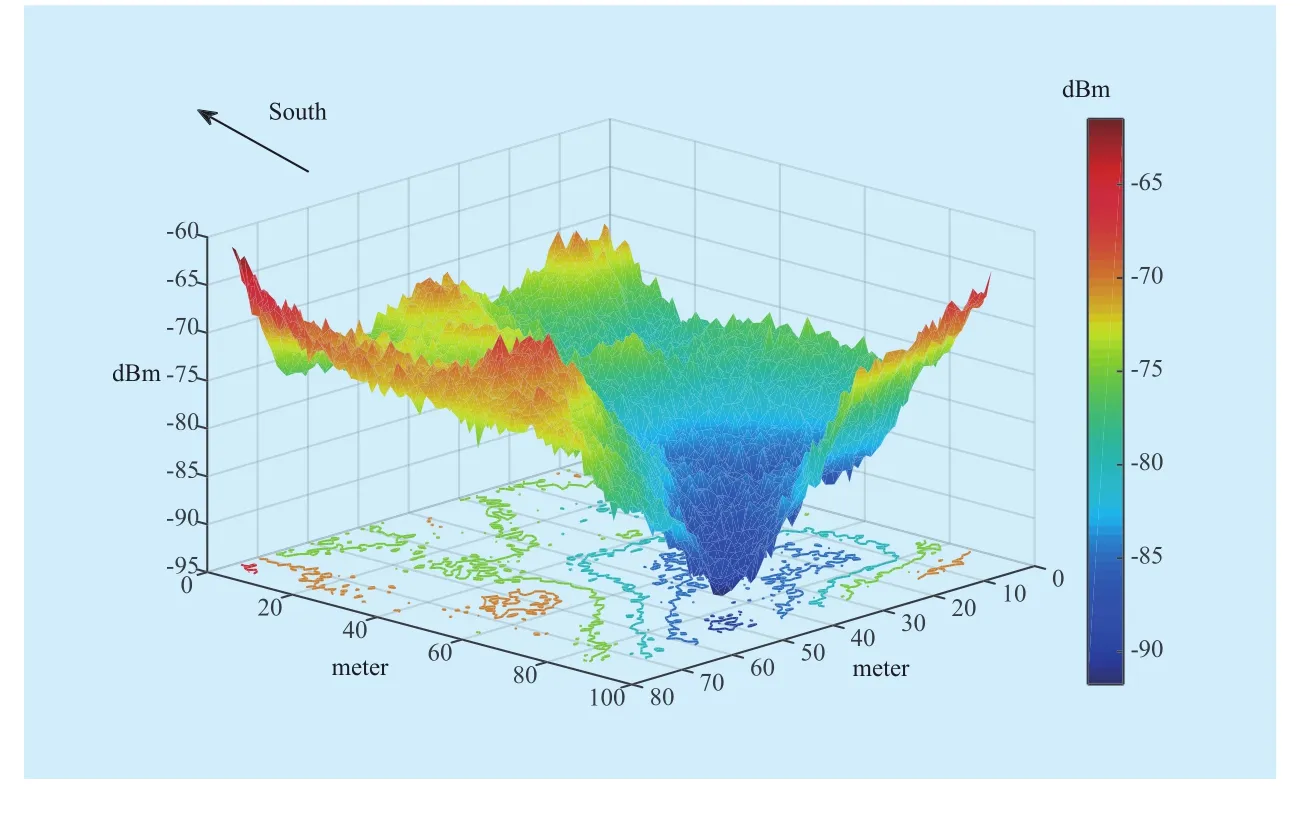
Fig. 5 REM of the selected area using ERSS

Fig. 6 REM of the selected area using symmetric sampling

Fig. 7 Probability distribution of signal strength

4.3.1 Spatial correlation

To check out whether the states of TV channels are correlated in the spatial domain, the MCFs are obtained by calculating the cross correlation of the TV channels over different meshes. The MCF is viewed as a random variable and its cumulative probability function is plotted in Figure 8, illustrating the distribution of dependence. The solid line shows that almost 50% of the MCFs among adjoining meshes are in the interval of [0.3, 0.7], suggesting approximately 50% meshes in TV service are highly correlated. When spatial separation increases, the dash-dot line shows a 5% decrement of mesh correlation, which indicates that the spatial correlation becomes weaker with the increased spacing. This can be explained by the fact that the adjoining meshes may experience the similar fading caused by building blockage and path loss, while the meshes located in different environment experience different channel environment.

4.3.2 Temporal correlation

The autocorrelation of the mesh state is utilized to obtain the temporal correlation. Figure 9 shows the autocorrelation coefficient decreases with the time delay, and the high time delay results in a fast decrease of the autocorrelation. Note that mesh states in two time slots may be significant to estimate the current state, and thereby a second order Markov chain is utilized to model this dependence.

V. MEASUREMENT DATA TESTING AND SCHEME ANALYSIS

To test our proposed scheme, half of the recordings are utilized to train our estimation model, and the rest data is used to verify the performance.

Generally speaking, false alarm probabilityand miss detection probabilityare widely used to evaluate the performance of spectrum sensing [25], and these two metrics are defined as follows.

Figure 10 illustrates the performance comparison of the proposed method and Markov based predication approach. Note that the order of Markov chain is set as 2. It can be observed that the average accumulative error curves ofandincrease with time slots,and our scheme outperforms the Markov based method, a 35% decrement inis achieved,andis reduced by 26%, indicating that adding spatial correlation into spectrum predication improves the estimation accuracy.

In our scheme, all potential meshes are clustered intohighly related groups, andmeshes are detected in each group, the sensing consumption is controlled by the total number of DMsThe relationship among these three parameters is. To quantify the efficiency of our scheme,we utilize EG to evaluate the saved sensing consumption using our scheme compared with the traditional sensing scheme that detects the meshes one by one, and EG is defined as

To verify the performance of our scheme under different EGs, the Uncertainty based Update (UU) algorithm is selected as the comparison since the similarity with our method,and it is noted that the channel correlation utilized in UU is limited to spatial correlation in our scenario.

Fig. 8 The cumulative probability of mesh correlation factor

Fig. 9 The autocorrelation of mesh states

Fig. 10 Accumulated error of false alarm and miss detection

Fig. 11 Performance comparison with UU approach

Figure 11 plots the performance comparison of UU and our scheme. Note that onlycan be adjusted in UU, we setas1to meet the same condition. It is illustrated that our scheme surpasses UU inandunder every EG, this can be explained by the fact that UU only utilizes the spatial correlation among meshes without considering the dependence between the current and historical mesh states. Compared to UU,andare reduced using our scheme when EG=0.5, suggesting that the sensing consumption is half reduced with less performance loss than UU, which means the proposed scheme is more significant for practical applications.

In addition, Figure 11 shows the performance of our algorithm decreases with EG,which verifies that the tradeoff between the efficiency and estimation accuracy. This tradeoff can be explained by two distinguishable situations. For a givenwe can either cluster more groups and select less DMs in each group or put meshes in fewer groups with more DMs in one group. In other words,our algorithm can adjust bothandwhich UU fails. Therefore, it is necessary to explore the joint influence ofandon performance. Figure 12 shows the additional performance increment is achieved by settinglarger than1with different EGs,which indicates the significance of introducingas a degree of freedom in the model parameters. Moreover, the optimaldecreases with EG. This can be explained as follows. When EG is largeis small)andis large, the meshes are clustered into fewer groups with a large number of EMs in each group, the selected DMs may be not highly correlated with all EMs. Thus, loweringresults in more correlated groups is a good option. However, when EG decreases andincreases, meshes in each groups are highly correlated, the cooperation among DMs begin to show the increment on performance. In this case, selecting more DMs in each group is a better choice. On these bases,we conclude thatshould be adjusted according to efficiency to optimize the performance.

VI. CONCLUSION

In this paper, we proposed a novel RSS scheme in which states of some meshes are estimated rather than all detected directly to reduce energy consumption and time delay.With MCM clustering algorithm, meshes are clustered into highly related groups and some representatives are selected to be detected while other meshes are estimated according to spatial correlation and autocorrelation respectively. A minimum entropy principle is proposed to merge the conflicting results conducted by these two estimations. Measurement data acquired by radio environment mapping is utilized to test our scheme, and the result shows the consumption of RSS is largely reduced with slight loss in accuracy, and the tradeoff between accuracy and efficiency can be adjusted to the practical conditions by setting the changeable number of DMs in each group.

ACKNOWLEDGEMENTS

The authors would like to thank the reviewers for their detailed reviews and constructive comments, which have helped improve the quality of this paper. This work was supported in part by National Natural Science Foundation of China under Grants (61525101,61227801 and 61601055) and in part by the National Key Technology R&D Program of China under Grant 2015ZX03002008.

Note

1. A small part of this work [26] was published in Crowncom 2015.

[1] Genachowski andet al,“In the Matter of Unlicensed Operation in the TV Broadcast Bands:Second Report and Order and Memorandum Opinion and Order”,Federal Communications Commission, 2013.

[2] S. Haykin, “Cognitive Radio: Brain-empowered Wireless Communications”,IEEE Journal on Selected Areas in Communications, vol. 23, no. 2,pp. 201-220, 2005.

[3] J. Mitola G. Maguire, “Cognitive Radio: Making Software Radios More Personal”.IEEE Personal Communications, vol. 6, no. 4, pp. 13-18, 1999.

[4] M. Barrie, S. Delaere, S, G. ukarevičienė andet al,“Geolocation database beyond TV white spaces? Matching applications with database requirements”,IEEE International Symposium on Dynamic Spectrum Access Networks (DYSPAN),Bellevue, Washington, USA: IEEE Press, 2012:467-478.

[5] A. Stirling, “Exploiting hybrid models for spectrum access: Building on the capabilities of geolocation databases”,IEEE International Symposium on Dynamic Spectrum Access Networks(DYSPAN), AACHEN, Germany: IEEE Press, 2011:47- 55.

[6] R. Caromi, Y. Xin, L. Lai, “Fast Multiband Spectrum Scanning for Cognitive Radio Systems”,IEEE Transactions on Communications, vol. 61,no. 1, pp. 63-75, 2013.

Fig. 12 Estimation accuracy VS. efficiency

[7] X. Xing, T. Jing W. Cheng andet al, “Spectrum prediction in cognitive radio networks”,IEEE Wireless Communications, vol. 20, no. 2, pp. 90-96, 2013.

[8] J. Han, H. Cheng, D. Xin andet al,“Frequent Pattern Mining: Current Status and Future Directions”,Data Mining and Knowledge Discovery,vol. 15, no. 1, pp. 55-86, 2007.

[9] A. Ng, A. Fu, “Mining Frequent Episodes for Relating Financial Events and Stock Trends”,Advances in Knowledge Discovery & Data Mining,Pacific-asia Conference. Seoul, Korea: Springer,2003: 27-39

[10] V. Tumuluru, P. Wang, D. Niyato, “A Neural Network Based Spectrum Prediction Scheme for Cognitive Radio”,IEEE International Conference on Communications (ICC). Cape Town, South Africa: IEEE Press, 2010: 1-5.

[11] V. Tumuluru, P. Wang, D. Niyato, “Channel Status Prediction for Cognitive Radio Networks”,Wireless Communications and Mobile Computing,vol. 12, no. 10, pp. 862-874, 2012.

[12] X. Xing, T. Jing, Y. Huo andet al, “Channel Qual-ity Prediction based on Bayesian Inference in Cognitive Radio Networks”,Proceedings of IEEE INFOCOM. Turin, Italy: IEEE Press, 2013: 1465-1473.

[13] Z. Wen, T. Luo, W. Xiang andet al, “Autoregressive Spectrum Hole Prediction Model for Cognitive Radio Systems”,IEEE International Conference on Communications Workshops. Beijing,China: IEEE Press, 2008: 154-157.

[14] A. Gibson, L. Arnett, “Statistical Modeling of Spectrum Occupancy”,Electronics Letters. vol.29, no. 25, pp. 2175-2176, 1993.

[15] Z. Chen, R. Qiu, “Prediction of Channel State for Cognitive Radio Using Higher-order Hidden Markov Model”,Proceedings of the IEEE SoutheastCon. Concord, NC, USA: IEEE Press, 2010:276-282.

[16] S. Geirhofer, L. Tong, B. Sadler, “Dynamic Spectrum Access in the Time Domain: Modeling and Exploiting White Space”,IEEE Communications Magazine. vol. 45, no. 5, pp. 66-72, 2007.

[17] S. Yin, D. Chen, Q. Zhang andet al, “Prediction Based Throughput Optimization for Dynamic Spectrum Access”,IEEE Transactions on Vehicular Technology. vol. 60, no. 3, pp. 1284-1289,2011.

[18] S. Yin, D. Chen, Q. Zhang andet al, “Mining Spectrum Usage Data: A Large-Scale Spectrum Measurement Study”,IEEE Transactions on Mobile Computing, vol. 11, no. 6, pp. 1033-1041,2012.

[19] H. Yilmaz, T. Tugcu, S. Bayhan, “Radio environment map as enabler for practical cognitive radio networks”,IEEE Communications Magazine,vol. 51, no. 12, pp. 162-169, 2013.

[20] M. Anders, “Symmetric Sampling Procedures,General Epidemic Processes and Their Threshold Limit Theorems”,Journal of Applied Probability, vol. 23, no. 2, pp. 265-282, 1986.

[21] P. Baldi, S. Brunak, “Information Theory, Entropy, and Relative Entropy. Bioinformatics : The Machine Learning Approach”,MIT Press. Cambridge, Massachusetts, USA . 2001: 357-363.

[22]Chinese National Standard GB 20600-2006.Channel coding and modulation for digital television terrestrial broadcasting system[S]. 2006.

[23] S. Zhang, W. Liu, “An Application of Simulated Annealing Algorithm for Soil Sampling Designing”,International Conference on Computer Science and Service System. Nanjing, China: IEEE Press, 2012: 1856-1859.

[24] I. Couckuyt, S. Koziel, T. Dhaene Kriging,“co-kriging and space mapping for microwave circuit modeling”,European Microwave Conference. Manchester, England: IEEE Press, 2011:444-447.

[25] T. Yucek, H. Arslan, “A Survey of Spectrum Sensing Algorithms for Cognitive Radio Applications”,IEEE Communications Surveys and Tutorials, vol. 11, no. 1, pp. 116-130, 2009.

[26] S. Huang, Y. Huang, H. Zhou andet al, “Spatial Spectrum Holes in TV Band: A Measurement in Beijing”,International Cognitive Radio Oriented Wireless Networks Conference. Doha, Qatar:Springer, 2015: 585-592.