Application of Bayesian Compressive Sensing in IRUWB Channel Estimation
2017-05-09SongLiuShaohuaWuYangLi
Song Liu, Shaohua Wu, Yang Li
Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, China
* The corresponding author, email: hitwush@hit.edu.cn
I. INTRODUCTION
Impulse radio ultra-wideband (IR-UWB) is a new type of wireless communication technology, which has advantages of strong anti-interference ability, low power consumption, high confidentiality, and low transmitted power. It well satisfies the requirements of high speed wireless transmission from close range, and almost cause no interference to other communication system in the same frequency, thus can solve the transmission problems of traditional wireless technology for many years[1][2][3].
In the Impulse Radio UWB communication, the data transmission is by sending a series of ultra-short duration pulses, typically on the level of nanosecond or sub-nanosecond in time domain to carry information. However,the bandwidth of IR-UWB signal occupied is extremely high, range from 1Ghz to 10Ghz in the frequency domain. It is very difficult to design high-speed and high-precision analog-to-digital converters (ADCs) in the receiver with low cost and low power consumption at the development of state of the art, which becomes the major restricting factors and seriously obstructs the practical application of IRUWB system. Therefore, some existing work has put forward the receiving scheme without Nyqusit sampling rate, such as incoherent ED(energy detection)[4]method, TR (transmit-reference)[5], and DTR (differential transmit-reference)[6]methods. However, the ED method is very sensitive to noise, and the TR and DTR method both not only make the hardware more complexity, but also cannot effectively combat the inter symbol interference (ISI).
A novel IR-UWB channel estimation scheme based on the Bayesian compressive sensing(BCS) framework is proposed in this paper to obtain the channel estimation.
In traditional IR-UWB system, there are mainly two approaches of channel estimation[7]. One is the auxiliary framework based on data, which employs analog delay units to yield a long-symbol to estimate the combination of pulse multipath channel. Plenty of analog units will cause the high power consume, which is not in conformity with the system. Another employs the maximum likelihood method to estimate the optimal value of the path gains and path delay time, which typically demand a tens GHz order sampling rate, and the design of hardware is extremely difficult.
The emerging of compressive sensing[8][9]theory provides a new solution for the design of practical IR-UWB receiver[10]. The IR-UWB signal carries information with ultra-short duration pulses, and propagates through the multipath channels, the received signal remain sparse in time domain. CS enables the reconstruction of sparse signals from a small set of random measurements and makes it possible for the receiver to reconstruct the signal accurately with sampling rates far below the Nyqusit rate of twice the bandwidth.
In recent years, the CS theory has been widely used in the filed of communication,such as wireless multi-hop networks[11], end to end network traffic reconstruction[12], and so on. Under the guidance of CS theory, compressive sensing in IR-UWB system is mostly used to deal with channel estimation and signal detection[13]. In Bayesian framework,compressive sensing reconstruction problem be represented based on sparse prior[14]. In[15], a hierarchical form of Laplace priors on signal coefficients is taken into consideration in Bayesian compressive sensing (BCS). In[16], a Laplace prior based distributed BCS algorithm in [15] has been modified for joint reconstruction of received signals and gets the channel parameters in the multiuser UWB communication network system. In [17], the proposed approach in [14] has been considered for UWB channel estimation, which relies on the time domain sparse of the channel impulse response and prior knowledge of channel property. In [18], an enhanced Bayesian learning produce is proposed to reconstruct the sparse UWB signal from a small collection of random projection measurements. In [19],different channel models are considered into the channel estimation with BCS method.However, those approaches just consider the sparseness of UWB channel in time domain,and abundant prior knowledge of the channel property do not take into consideration, such as sparse structure and the statistical information of the UWB channel.
In this paper, motivated by exploiting the statistical prior information of the UWB channel, we propose an IR-UWB channel estimation approach based on cluster struct prior of channel which the arrival of multipath impulse response with clusters and the Poisson process of arrival time of rays in a cluster. Comparing with the conventional CS reconstruction algorithm and BCS reconstruction algorithm, our approach has the advantage of higher reconstruction accuracy, better BER, and noise robust in some text and no need extra hardware overhead.
The rest of this paper is organized as follows: Section II gives a brief description of the IR-UWB signal model, channel model and the BCS theory background. Section III introduce the CS based receiver and presents the modified BCS with cluster struct prior. Our simulation results and discussion are given in Section IV, followed by our conclusions and future work in Section V.
II. IR-UWB SYSTEM MODEL AND BAYESIAN COMPRESSIVE SENSING
2.1 The IR-UWB communication signal model
Compared with the traditional communication technology, IR-UWB communication technology transmits a series of information pulses without carrier modulation. In the signal user UWB communication system, transmitted signal is divided into two parts: the first parts know as training symbols which used for channel estimation, which launch mono-pulse in a symbol period; Followed by the data symbols part, which can be modulated with different methods, such as PPM, PAM, BPM and joint modulation.
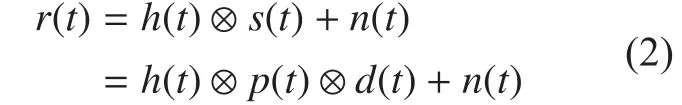
Due to most of the multipath components are negligible,is especially sparse in the time domain. In addition, because of the ultra-short duration pulses, the transmitted IRUWB signalis also extremely sparse in the time domain, and the bandwidth of IR-UWB signal is very high in the frequency domain.
2.2 UWB channel model
In the classical Saleh-Valenzuela channel model, the multi-path components arrival with clusters, the arrival time of rays in one cluster follow the Poisson distribution. The channel impulse responses can be modeled as:

2.3 Compressive sensing overview
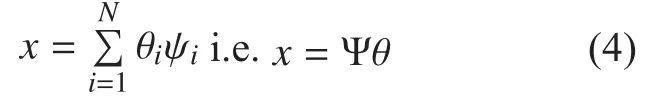
The compressive measurement sequencecan be obtain via the linear measurements with a measurement matrix

Fig. 1 Saleh-Valenzuela channel model

In the standard CS framework, signal reconstruction problem mainly solved by convex optimization method, such as basis pursuit(BP), and greedy algorithms such as matching pursuit (MP) and orthogonal matching pursuit(OMP).
2.4 Bayesian compressive sensing
Based on the statistical information of the measurement signal and the prior knowledge of the signal in the sparse domain, CS is represented in the Bayesian framework. The compressive measurement be reconsidered with measurement noise and additive noise as


As mentioned above, the coefficient is sparse constraint. A widely used sparseness prior is the Laplace density function:

Hence the solution in (8) corresponds to the maximum a posterior estimation forwith the prior in (9).
However, the Laplace prior is not conjugate to the Gaussian likelihood and the associated Bayesian inference may not be performed in closed form. The relevance vector machine(RVM) has been imposed, which has the similar properties as the Laplace prior but allows convenient conjugate-exponential analysis.The zero-mean Gaussian prior is considered over each element of,


By marginalizing over the hyper-parameters, the overall prior onis

Based on the above discussion, the Bayesian linear model considered on RVM is essentially one of simplified models for Bayesian model selection. We can express the posterior foras a Gaussian distribution with mean and variance given by



III. BAYESIAN COMPRESSIVE SENSING CHANNEL ESTIMATION BASED ON CLUSTER LOCATION PRIOR
In this section, we will first give the redesigned CS-based IR-UWB communication system and describe our novel reconstruction algorithm under this framework follow on.
The main structure of CS-based IR-UWB receiver is given in Fig.2. The compressive measurement produce is finished in the analog frontend, and signal processing is been done in the digital backend.
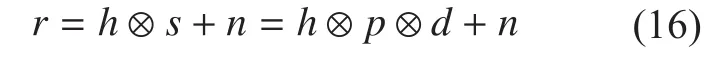


In the channel estimation, considering the quasi-static of the UWB channel, we propose a two-stage measurement estimation method. In the first stage, we obtain the cluster statistical prior of the channel via a deterministic matrix.In the second stage, we estimate the channel impulse response with the random sampling sequences and the cluster location set.
In the first stage, the pilot signal is projected to a low dimensional space with matrixand we obtain the measurement sequence

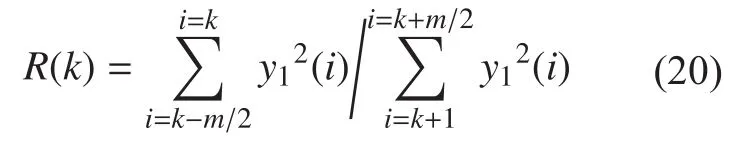
In the second stage, the reconstruction sparse signal is channel impulse response. After getting the cluster location set, projecting the received signal on a random Bernoulli matrix

Fig. 2 Illustration of CS-based IR-UWB receiver



Fig. 3 The performance of channel estimation: using cluster prior and no cluster prior

Fig. 4 BER with different channel estimation results
In the process of Bayesian analysis, by maximizing the edge probability function to estimate the high-dimensional parameter about. The relevance vector machine learning process is used into the algorithm. In each time of iteration, make judge to the position that algorithm search, retain those position which the cluster location set contained. When it satisfy the termination condition, the mean valueswhich can be seen as the estimation of channel impulse responses.
IV. SIMULATION RESULTS
In this section, our simulation results will be presented. The pilot signal pulse waveform we send is the second order differential Gaussian pulse, pulse duration timePulse shaping factor is 0.25. The system virtual sampling frequencyThe UWB channel model used for simulation is IEEE802.11.4a CM1 of residential line of sight (LOS) environment. And the parameters of CM1 are given as follow:The frame time

In the part of signal demodulation, the reconstruction mapping method[21]is introduced in the paper, and the channel estimation results are used. The number of observations isM=200. Signal modulation method is BPM-2PPM, the number of iterations is 1. Fig.4 shows the simulation results.
We note that, our approach is superior to the ordinary BCS reconstruction method. The RSNR of our method is higher than the BCS method about 1.5~3dB. The channel estimation results are used in the signal demodulation shows our approach have better performance.
V. CONCLUSIONS
In this paper, the time domain sparseness of the IR-UWB signal and channel are considered into the BCS framework to realize highspeed IR-UWB communication. Based on the existing research, we focus on the channel statistical prior information, using a two-stage measurement estimation method to obtain the channel estimation. Simulation results show that our approach is better than ordinary BCS algorithm, and have a good performance in the signal demodulation.
In the future work, we will improve the cluster identified algorithm with better noise robustness. Besides, combined with the other prior information of IR-UWB channel, we will increase the performance of the IR_UWB channel estimation and signal demodulation in the future.
ACKNOWLEDGEMENTS
This work was sponsored by the National Natural Science Foundation of China (Grant Nos.61001092, 61371102).
[1] M.Win and R. Scholtz, Ultra-Wide Bandwidth Time-hopping Spread Spectrum Impulse Radio for Wireless Multiple-access Communications,IEEE Trans. Commun., vol. 48, pp. 679–689, April 2000.
[2] R. C. Qiu, H. P. Liu, and X. Shen, Ultra-Wideband for Multiple Access,IEEE Commun. Mag., vol.43, pp. 80–87, February 2005.
[3] R. C. Qiu, R. Scholtz, and X. Shen, Ultra-Wideband Wireless Communications–A New Horizon,IEEE Trans. Veh. Technol., Editorial on Special Issue on UWB, vol. 54, September 2005.
[4] A. A. D’ Amico, U. Mengali, E. A. de Reyna, Energy-Detection UWB Receivers with Multiple Energy Measurements,IEEE Trans. Wireless Commun. 2007, 6 (7): 2652–2659
[5] T. Q. S. Quek, M. Win, Analysis of UWB Transmitted-Reference Communication Systems in Dense Multipath Channels,IEEE J. Select. Areas Commun. 2005, 23 (9): 1863–1874
[6] Y.-L. Chao, R. A. Scholtz, Optimal and Suboptimal Receivers for Ultra-Wideband Transmitted Reference Systems, Proc.IEEE Global Telecom.Conf. 2003, 2: 759–763
[7] Anand Oka and Lutz Lampe, A compressed sensing receiver for UWB impulse radio in bursty applications like wireless sensor networks,Physical Communication, vol. 2, pp. 248-264, Dec. 2009
[8] D. Donoho, Compressed sensing,IEEE Trans. on Inf Theory, vol. 52, no.4, pp. 1289-1306, April 2006.
[9] E. J. Candès, M. B. Wakin. An Introduction To Compressive Sampling,IEEE SIGNAL PROCESSING MAGAZINE, 2008, 25(2): 21-30
[10] Z. Wang, G. R. Arce, J. L. Paredes, and B. M.Sadler, Compressed Detection For Ultra-wideband Impulse Radio,IEEE Sig. Proc. Adv. Wireless Comm. (SPAWC), 2007
[11] D. Jiang, Z. Xu. An multicast delivery approach with minimum energy consumption for wireless multi-hop networks.Telecommunication Systems, 2015, online available.
[12] L. Nie, D. Jiang, Z. Xu. A compressive sensing-based approach to end-to-end network traffic reconstruction utilizing partial measured origin-destination flows.Transactions on Emerging Telecommunications Technologies, Aug. 1,2015
[13] J. Paredes, G. R. Arce, and Z. Wang, Ultra-wideband Compressed Sensing: Channel Estimation,IEEE J. Select. Topics Signal Proc., vol. 1, pp.383–395, Oct. 2007
[14] Ji S, Xue Y, Carin L. Bayesian compressive sensing[J]. Signal Processing,IEEE Transactions on,2008, 56(6): 2346-2356.
[15] Babacan S D, Molina R, Katsaggelos A K. Fast Bayesian compressive sensing using Laplace priors[C]//Acoustics, Speech and Signal Processing, 2009. ICASSP 2009. IEEE International Conference on. IEEE, 2009: 2873-2876.
[16] Liang T, Zheng Z, Lei S. UWB Channel Estimation Based on Distributed Bayesian Compressive Sensing[J].JDCTA: International Journal of Digital Content Technology andits Applications,2011, 5(2): 1-8.
[17] Shi L, Zhou Z, Tang L, et al. Ultra-wideband channel estimation based on Bayesian compressive sensing[C]//Communications and Information Technologies (ISCIT), 2010 International Symposium on. IEEE, 2010: 779-782.
[18] Cheng X, Guan Y L, Yue G, et al. Enhanced Bayesian compressive sensing for ultra-wideband channel estimation[C]//Global Communications Conference (GLOBECOM), 2012 IEEE.IEEE, 2012: 4065-4070.
[19] Ozgor M, Erkucuk S, Çirpan H A. Bayesian compressive sensing for ultra-wideband channel models[C]//Telecommunications and Signal Processing (TSP), 2012 35th International Conference on.IEEE, 2012: 320-324.
[20] Candès E J, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information [J].Information Theory, IEEE Transactions on, 2006,52(2): 489-509.
[21] Yao H, Wu S, Zhang Q, et al. A compressed sensing Approach for IR-UWB Communication[C]//Multimedia and Signal Processing(CMSP), 2011 International Conference on. IEEE,2011, 2: 3-7
杂志排行
China Communications的其它文章
- A Reliable Routing Algorithm with Network Coding in Internet of Vehicles
- Multi-Owner Keyword Search over Shared Data without Secure Channels in the Cloud
- Microblog User Recommendation Based on Particle Swarm Optimization
- A User Participation Behavior Prediction Model of Social Hotspots Based on Influence and Markov Random Field
- Ethics Aware Object Oriented Smart City Architecture
- Walsh Hadamard Transform Based Transceiver Design for SC-FDMA with Discrete Wavelet Transform
