无黏结支撑的轨道板板角离缝研究
2017-05-09赵磊孙璐孙伟赵国堂
赵磊 孙璐 孙伟 赵国堂
摘要:为研究温度影响下的高速铁路无砟轨道板翘曲变形和变化规律,基于最小势能原理,利用傅里叶级数模拟轨道板翘曲过程的翘曲变形,对负温度梯度引起的板角离缝进行研究。利用京沪高速铁路CRTSⅡ型轨道板现场实测的板角翘曲数据,验证本文用于计算轨道结构翘曲变形的基于最小势能原理的计算方法,分析温度梯度影响下的轨道板翘曲规律。对比结果表明:新方法得到的计算结果和实测数据得到的数据吻合较好,验证了该方法的可靠性。研究结果表明:板端翘曲变形与温度梯度变化成正相关性,增大地基系数可以有效地减小温度引起的轨道板板端翘曲变形。
关键词:轨道结构;板角离缝;势能方程;傅里叶级数;拟Newton迭代
中图分类号:U238 文献标识码:A
与传统有砟轨道相比,高速铁路无砟轨道具有乘坐舒适、方便快捷、运输能力强等优势,因此成为铁路客运专线发展的必然选择。随着高速铁路的迅速发展,板中隆起、板端翘曲引起的平顺性衰减严重地影响着高速铁路运行的安全。太阳照射会使轨道板“上热下冷”,强降温等会造成轨道板表面的温度骤然降低,使得轨道板“上冷下热”。这种在轨道板厚度方向上产生的温度梯度荷载会导致轨道板产生周期性的翘曲变形,对设计使用寿命要求不小于60年的无砟轨道结构,需考虑温度变形的长期疲劳效应。
国内外学者对水泥路面混凝土板的温度翘曲变形研究较早。Choubane等考虑了非线性温度梯度对水泥铺面的影响,采用二次方程表述非线性温度曲线,研究了非线性温度梯度对温度应力和变形的影响。William等通过建立精细化的具有传力杆的混凝土路面模型,研究了路面温度应力及温度变形。Belshe等通过测量混凝土路面路表和板底温度变化,对混凝土路面温度翘曲问题进行了研究,通过数值模拟对影响铺面垂向位移的因素进行了分析。Nam等通过测量1 d中机场铺面的挠度变化,对机场铺面温度翘曲问题进行了研究,通过数值模拟对影响铺面垂向位移的因素进行了分析。
随着无砟轨道的广泛应用,国内学者和机构对无砟轨道结构的翘曲变形也进行了深入研究。王继军等利用有限单元法研究了单元板式无砟轨道板温度翘曲变形问题。刘钰等通过在不同气候条件下现场观测CRTSⅡ轨道板温度,得到实测的轨道板温度梯度,建立了轨道结构力学有限元模型,计算轨道板在实测温度梯度作用下的温度翘曲变形。卢炜针对严寒地区哈大客运专线上CRTSⅠ型轨道板与充填层砂浆四角离缝的实测结果,探讨CRTSⅠ型轨道板四角离缝成因,提出了减小离缝的施工应对措施。王雪松等通过建立CRTSⅡ的力学模型,分析轨道板的不同负温度梯度,以及轨道板与砂浆层之间不同的黏结条件对轨道系统受力与变形的影响。戴公连等通过对客运专线曲线段简支梁桥上纵连板式无砟轨道结构温度场的连续观测,研究了秋季多种天气情况下曲线桥上无砟轨道温度场的时变规律。这些成果对分析与了解无砟轨道结构的翘曲变形有极大帮助,但对无砟轨道结构翘曲变形的研究多停留在观测层面上,对轨道板的温度翘曲变形理论研究较少,因此,对无砟轨道结构翘曲变形规律开展研究具有重要的意义。
综上所述,现有无砟轨道结构温度翘曲变形的研究方法,有解析法和有限元法两种。解析法多采用威斯特卡德理论,假设板与地基始终保持接触,无空隙,推演了板由于地基约束而产生的翘曲变形;有限元法通过建立无砟轨道结构模型,设置相应的材料热力学参数和边界条件,得到结构的变形与内力。然而这两种方法各有缺点:威斯特卡德解假设板与地基始终保持接触,无空隙,与无砟轨道温度翘曲变形后产生离缝的实际状况不符。有限元方法,建模方法不统一,结果受模型尺寸、网格大小、边界条件影响较大,不利于工程设计。本文基于能量法的轨道板翘曲变形研究,采用傅里叶级数来模拟轨道板翘曲过程中的翘曲曲线,根据拟Newton迭代算法求得轨道板翘曲曲线方程。文中对不同温度梯度和不同地基系数下轨道板的翘曲变形量进行了分析,探讨了降低板角离缝的方法。
1轨道板翘曲变形计算模型
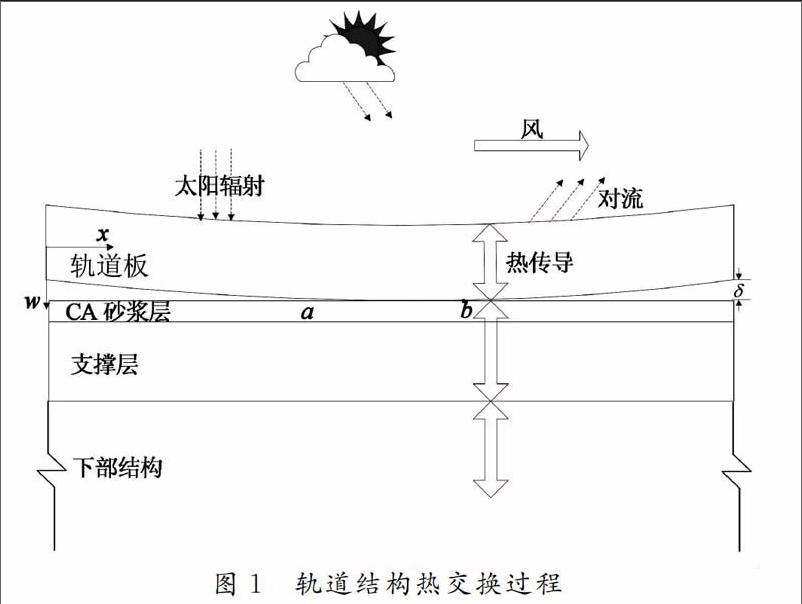
传导、对流、热辐射是组成无砟轨道结构热量平衡的3种基本传热方式。无砟轨道通过热辐射和对流过程获得热量,以热传导的形式在无砟轨道结构内部传递,轨道结构热交换过程如图1所示。当板内温度梯度较大时,无砟轨道板会发生翘曲变形。当翘曲变形受重力作用、砂浆层的黏结作用以及钢轨和扣件系统的约束作用时,板内会产生翘曲应力,如图2所示。温度应力是导致无砟轨道结构早期开裂的重要因素。图3所示为典型无砟轨道结构横断面图,结构自上向下分别为轨道板、砂浆层和支撑层。
2基于能量法的轨道板翘曲变形研究
无砟轨道结构随温度变化产生翘曲变形,导致与支撑层连接处产生离缝,引起轨道平顺性衰减,在高速列车动荷载作用下,离缝处的轨道板与基础反复弯曲变形,造成板端破碎以及支撑层剥离和破碎,形成安全隐患。轨道板的翘曲变形分为2种:一种是轨道板表面温度高于内部温度,造成“上热下冷”的情况,此时轨道板中部拱起,板角下沉。另一种是轨道板表面的温度骤然降低,使得轨道板“上冷下热”,此时产生如图2所示的板角上翘,板中下沉。图4所示为轨道板微分单元受力模型,轨道板在线性温度梯度作用下,产生如图所示的温度应力。当板表面温度高于板底温度时,板中部拱起,此时受板的自重、钢轨和扣件系统的约束作用,拱起量较小;当板表面温度低于板底温度时,板角由于后浇带的存在,容易在荷载和温度作用下产生应力集中,后浇带开裂,板角翘曲量大,形成表面裂缝。裂缝的张开宽度与结构的耐久性有密切关系,裂缝开裂宽度过大,会使钢筋腐蚀加剧,结构加速破坏,板角翘曲比板中拱起更为不利。
无砟轨道为曝露于大气环境下的条带状结构物,CRTSⅡ型轨道板采用了预应力筋低放用于抵抗板檐上翘的设计理念,横向翘曲量小,本文研究中忽略轨道板的横向弯曲,将轨道板简化为梁构件。将轨道板下部支撑结构假设为温克勒地基,即支撑刚度简化为一系列独立的线性弹簧。板端在翘曲过程中受到板端接缝的约束作用,该约束作用以接缝嵌锁模量(modulus of interlocking joint)表征,該模量值是集料尺寸、接缝开裂宽度、接缝接触面积的函数。
采用傅里叶级数来模拟轨道板翘曲过程中的翘曲曲线,并假设轨道板两端的翘曲值相等。考虑板端的边界条件,同时兼顾级数可导性,可将轨道板翘曲曲线用式(1)表示。
(1)式中:ω0,ω1,…,ωn为挠曲线的待定系数;l为轨道板计算长度;n为级数计算次数。
轨道板的弯曲变形能U1为:
(2)式中:E为轨道板弹性模量;J为轨道板截面惯性矩;L为轨道板计算长度。
轨道板翘曲,轨道板与支撑结构部分脱离,脱离点在计算坐标系(如图1所示)的坐标分别为a和6,此时轨道板的弹性支撑变形能U2为:
(3)式中:k为支撑轨道板的弹性地基系数;B为轨道板宽度。
板端在翘曲过程中受到板端接缝的约束作用(如图2所示)的变形能U3为:
(4)式中:ks为接缝嵌锁模量。
温度梯度做功V:
(5)
由能量法计算获得的傅里叶级数的系数衰减迅速,通过计算分析可知(见表1),当取到级数的第二项时,其系数已经非常小,基本可以忽略。为简化计算,取傅里叶级数的前两项,即
(6)
(7)
(8)
(9)
(10)
轨道板的真实位移函数ω应该使总势能Ⅱ为最小值,即叫应该使Ⅱ的一阶变分为零,即
(11)
将式(4)(7)(8)(9)代入式(10),总势能函数Ⅱ将变成ω0,ω1,ω2的函数,根据最小势能原理,这些待定常数应使总势能函数Ⅱ为极值,因此必须有:
(12)
同时,轨道板翘曲脱离点a和b应满足翘曲曲线方程,即:
(13)
(14)
式(12)(13)(14)是5个待定常数的非线性方程组,本文求解采用拟Newton迭代算法(如图5所示),即可解出未知数,矩阵Ak+1关于点{x}k及{x}k+1具有“差商”性质。
3轨道板翘曲变形计算分析
3.1计算方法验证
京沪高铁铺设CRTSⅡ型轨道板时,在某路段对3块相连轨道板的周围空气温度、轨道板温度、翘曲变形值进行了实测。为测量轨道翘曲变形,用千分表观测,将6个千分表分别布置在板角和纵向板边缘中部。
为了验证本文算法的正确性,取标准CRTSⅡ轨道板进行分析,轨道板宽度为2.55 m,长度为6.45 m,厚度为0.2 m,泊松比μ为0.15,轨道板弹性模量E为3.55×104MPa,膨胀系数αE为1×10-5,地基反应模量为20 MPa/m,接缝嵌锁模量为0。7 MPa/m。用本文的方法计算轨道板角翘曲变形并与实测数据进行对比,如图6所示,可见本文的计算方法能够比较准确地用于轨道结构翘曲变形计算。图6(b)中,实测板角翘曲变形较计算值略大,原因是计算模型将轨道板简化为一维模型,未考虑另一方向翘曲变形对该方向的影响,同时由于计算过程中将温度梯度进行线性分布假设,未考虑非线性温度对轨道板的影响。然而计算与实测的变形差在温度梯度40℃/m仅有0.07 mm,对比结果进一步证明了本文关于轨道板翘曲变形计算方法的准确性和有效性。
3.2温度梯度影响下的轨道板翘曲规律
为了分析温度梯度对轨道板端部翘曲的影响,选取了6组不同的温度梯度进行分析,轨道板上下表面温差变化范围从2℃到12℃,变化幅度为2℃,见表1。由表1可知,当轨道板上下表面温差为2℃(温度梯度10℃/m)时,板端翘曲位移为0.198mm,板中心下沉量为0.226 mm;当轨道板上下表面温差为8℃(温度梯度40℃/m)时,板端翘曲位移为0.515 mm,约为温度梯度20℃/m时板端翘曲位移的2.6倍,板中心下沉量为0.553 mm,约为温度梯度10℃/m时板中心下沉量的2.4倍;当轨道板上下表面温差为12℃(温度梯度60℃/m)时,板端翘曲位移为0.686 mm,约为温度梯度10℃/m时板端翘曲位移的3.5倍,板中心下沉量为0.737mm,约为温度梯度10℃/m时板中心下沉量的3.3倍。
由图7和图8可知,随着轨道板温度梯度的变化,轨道板板端翘曲变形和板中心下沉量也相应变化。随着轨道板负温度梯度增大,板端翘曲变形增大,板中心下沉量也相应增加,与温度梯度变化成正相关性;轨道板板端翘曲变化与板中心下沉量变化和温度梯度变化均近似直线关系;在同一温度梯度时,板中心下沉量比板端翘曲变形量大。
3.3地基系数影响下的轨道板翘曲规律
为了研究地基系数对轨道板端部翘曲的影响,选取了5组不同的地基系数进行分析,地基系数变化范围为2×105~2×109Pa/m,见表2。
由表2可知,当地基系数为0.2 MPa/m时,板端翘曲位移为0.376 mm,相应板中心的下沉量为0.403 mm;当地基系数增大为20 MPa/m时,板端翘曲位移为0.343 mm,约为地基系数为0.2 MPa/m时板端翘曲位移的0.9倍,板中心的下沉量为0.368 mm,约为地基系数为0.2 MPa/m时板中心下沉量的0.92倍;当地基系数为2 000 MPa/m时,板端翘曲位移为0.020 1Tim,约为地基系数为0.2MPa/m时板端翘曲位移的0.05倍,板中心的下沉量为0.028 mm,约为地基系数为0.2 MPa/m时板中心下沉量的0.07倍。
由图9和图10可知,增大地基系数可以有效地减小温度引起的轨道板板端翘曲变形。随着地基反应模量增大,板端翘曲变形减小,板中心下沉量也相应减小,与地基反应模量变化成负相关性;轨道板板端翘曲变化和板中心下沉量变化均与地基反应模量变化呈非线性关系,突变点在地基反应模量为200MPa/m处。
为了减小负温度梯度引起的轨道板板端翘曲变形,轨道板下部结构应采用刚度较大的支撑层,然而轨道结构动力响应会随着弹性地基刚度增大而增大,因此需要结合轨道结构动力分析选择合理的地基刚度。
4结论
1)本文基于最小势能原理,利用傅里叶级数模拟轨道板翘曲过程的翘曲变形,对负温度梯度引起的板角离缝进行研究,根据拟Newton迭代算法求得轨道板翘曲变形以及翘曲曲线方程。该方法具有准确简单的特点,可以用于工程设计。
2)随着轨道板负温度梯度增大,板端翘曲变形增大,板中心下沉量也相应增加,与温度梯度变化成正相关性;轨道板板端翘曲变化与板中心下沉量变化与温度梯度变化均近似直线关系;在同一温度梯度时,板中心下沉量比板端翘曲变形量大。
3)增大地基系数可以有效地减小温度引起的轨道板板端翘曲变形。随着地基反应模量增大,板端翘曲变形减小,板中心下沉量也相应减小,与地基反应模量变化成负相关性。
4)为了减小负温度梯度引起的轨道板板端翘曲变形,轨道板下部结构应采用较大的弹性地基系数,然而轨道结构动力响应会随着弹性地基系数增大而增大,因此需要结合轨道结构动力分析选择合理的地基系数。
5)计算模型将轨道板简化为一维模型,未考慮另一方向翘曲变形对该方向的影响,同时由于计算过程中将温度梯度进行线性分布假设,未考虑非线性温度对轨道板的影响,这是以后工作中要考虑的内容。