外置金属阻尼器的新型自复位约束砌体墙抗震性能研究

胡晓斌　李文霞　刘坤　陈璐

摘要：研制了一种同时布置体内无黏结预应力筋和外置金属阻尼器的新型自复位约束砌体墙，通过拟静力试验研究了该自复位墙在低周反复荷载作用下的滞回性能，重点探明了预应力筋初始预应力、金属阻尼器屈服荷载大小对其耗能性能的影响，最后基于试验结果建立了数值分析模型。研究表明：该自复位约束砌体墙滞回曲线呈“旗形”，在较大位移下未出现明显的损伤，且在加载及卸载过程中没有明显的强度和刚度退化；随着预应力筋初始预应力的增加，墙体的自复位性能增强，但其耗能能力会降低；随着金属阻尼器屈服荷载的增大，墙体的耗能能力增强，但会产生少量的残余变形；数值模拟结果与试验结果吻合较好，表明本文所提出的分析模型能较好地模拟该自复位约束砌体墙的力学行为。

关键词：新型自复位约束砌体墙；外置金属阻尼器；拟静力试验；抗震性能；数值分析

中图分类号：TU352 文献标识码：A

自复位结构是一种新型的抗震结构形式，近年来得到了研究者和工程技术人员的高度重视。和传统的抗震结构相比，自复位结构最为突出的特点在于卸载后变形能完全或基本恢复。在强震作用下，自复位结构基本不产生残余变形，震后不需或经少量的维修即可恢复正常使用，从而大大地降低了震后修复成本。自复位结构体系可分为3种类型：自复位框架结构、自复位墙结构和自复位支撑框架结构，其中自复位墙主要由3部分组成：墙体、后张拉无黏结预应力筋和阻尼器。与普通的抗震墙不同，自复位墙在墙底（或沿墙高）设置水平缝，在水平荷载作用下，墙体能绕墙底两端产生微小的转动，即所谓的摇摆响应。

对于自复位墙结构，国内外少数学者开展了相关的理论分析、试验研究和数值模拟工作。在理论分析方面，Armouti首先建立了自复位混凝土墙的理论分析模型，其中混凝土墙简化成一个刚体，预应力筋采用弹簧来模拟，墙底与基础的接触采用位于两端的只受压连接模拟。在试验研究方面，Perez等设计了5个6层自复位混凝土墙进行拟静力试验，结果表明自复位混凝土墙能承受很大的非线性侧向变形而不发生显著的破坏，并且能保持自复位性能，不产生残余变形。Toranzo等对未布置预应力筋的自复位约束砌体墙，提出了直接基于位移的抗震设计方法，并对一缩比为40%的3层自复位约束砌体墙模型进行了振动台试验，试验模型考虑了楼板和边柱的作用。试验结果表明自复位约束砌体墙能极大地减小结构的损伤，提高传统砌体结构的抗震性能。在数值模拟方面，Kurama针对自复位混凝土墙，建立了基于DRAIN-2DX纤维模型梁柱单元的分析模型，并进行了非线性地震反应分析。Toranzo针对未布置预应力筋的自复位约束砌体墙，提出了用于有限元分析的数值分析模型，其中墙体采用桁架模拟，墙底设置一组只受压的弹簧来模拟墙和基础间的接触，阻尼器通过弹簧模拟。

从以上可看出，目前的研究主要针对自复位混凝土墙，对于自复位约束砌体墙的研究很少，且已有的研究中并未布置预应力筋，而预应力筋对于提高墙体的自复位能力具有重要意义。基于此，本文提出一种同时布置体内无黏结预应力筋和外置金属阻尼器的新型自复位约束砌体墙，首先通过拟静力试验研究该新型自复位墙在低周反复荷载作用下的滞回性能，然后基于试验结果，提出适用于该新型自复位约束砌体墙的数值分析模型。

1外置金属阻尼器的新型自复位约束砌体墙研制

1.1墙体构造

如图1所示，墙体采用砌体砌筑而成，周边设置混凝土构造柱和圈梁以提供约束，构造柱下部预埋双头螺栓以连接金属阻尼器。为防止墙体发生平面外倾覆，约束砌体墙置于凹槽型基础梁中。基础梁肩部预埋螺栓，通过连接件（图1（c））连接金属阻尼器。墙底及基础梁间设置水平缝，在水平荷载作用下，约束砌体墙可绕墙底两端产生微小的转动。预应力筋穿过竖向贯穿约束砌体墙及基础梁的预留管道，上下两端通过锚具锚固。

1.2金属阻尼器设计

约束砌体墙底部两端对称布置4个金属阻尼器，如图1（d）所示，其前端通过预埋螺栓与构造柱连接，后端通过螺栓与连接件相连。金属阻尼器采用Q235钢材加工制作。随着墙体的转动，该阻尼器绕后端发生转动，当受弯屈服后会产生较大的塑性变形，从而达到耗能减震的目的。为避免塑性变形集中，将金属阻尼器的耗能部位限制在一定长度的区域内，如图1（d）中阴影区域所示。此外，在容易发生应力集中的部位使用圆弧过渡。

金属阻尼器可简化为一变截面悬臂梁进行受力分析，如图1（d）所示，其中F表示阻尼器前端所受的荷载。设任一截面高度为h，此截面到作用点的距离为z，当全截面屈服时，设相应的屈服荷载为F_y，则有：

（1）式中：f_y为钢材屈服强度；W_p为计算截面的塑性截面模量；t为阻尼器的厚度。假设耗能区域各截面同时屈服，则由式（1）可得

（2）

由式（2）可知，金属阻尼器耗能区域两侧轮廓线应为抛物线，但为方便起见，实际加工时取为直线。

2拟静力试验概况

2.1试件设计

考虑到加载条件，墙体尺寸取为1 350 mm×1 000 mm×240 mm（高×宽×厚），混凝土構造柱及圈梁截面尺寸均为200 mm×240 mm（高×宽），基础梁截面尺寸为400 mm×600 mm（高×宽），其中凹槽深100 mm。此外，为便于施加预应力，在基础梁底部设置混凝土支墩，其尺寸为800 mm×600mm×600 mm（长×宽×高）。砌体墙采用MUIO蒸压灰砂砖砌筑，施工时预留管道周围的砌体需要进行切角处理。除支墩采用素混凝土外，其他混凝土构件均按照构造要求进行配筋，混凝土强度等级均为C20，纵筋采用HRB 335。预应力筋采用钢铰线1φ^s1×7（公称直径d=15.2 mm）。

为研究金属阻尼器对该新型自复位约束砌体墙抗震性能的影响，设计了2种不同尺寸的阻尼器，其厚度为10 mm，分别记做SD-1和SD-2，如图2所示。由式（1）可知，2种阻尼器的屈服荷载存在如下关系：

F_y2=4F_y1。 （3）式中：F_y1，F_y2分别表示SD-1和SD-2的屈服荷载。

2.2加载装置与测点布置

拟静力试验加载装置与测点布置如图3所示，水平荷载由60 t液压千斤顶施加，其加载端与连接支架连接。基础梁通过4个地锚栓锚固于试验室台座。共布置3个位移计，2个力传感器。其中，位移计1和2于墙顶左右两侧对称布置，用于测量墙顶的水平位移，位移计3用于测量自复位墙墙底的水平滑移；力传感器分别测量墙顶水平力及预应力筋在加载过程中的拉力。

2.3加载制度及工况

采用位移控制分级加载，如图4所示。第一级位移幅值为4 mm，随后以4 mm递增加载幅值，直到水平位移幅值达到20 mm（墙高的1.5%左右），每级加载循环1次。规定千斤顶对自复位约束砌体墙施加推力时，水平力及位移为正，反之为负。

为考察预应力筋初始预应力的影响，考虑了3种情况：未布置预应力筋，初始预应力为0，初始预应力为0.1f_ptk，其中f_ptk表示预应力筋强度标准值，其值为1 860 MPa。对于金属阻尼器，如前所述，也考虑了3种情况：未布置金属阻尼器，布置SD-1阻尼器及布置SD-2阻尼器。由以上可得9种工况，如表1所示，其中f_p0表示初始预应力。图5所示为试验现场照片。

3试验结果及分析

3.1金属阻尼器试验

为考察本文设计的金属阻尼器的耗能能力，使用30 t油压千斤顶对其进行了重复加载试验。采用位移控制加载，加载制度如图6（a）所示。试验中，金属阻尼器发生了明显的变形，如图6（b）所示。该金属阻尼器的力F-位移d滞回曲线如图6（c）所示，其形状饱满，表明本文设计的金属阻尼器具有良好的耗能性能。

3.2新型自复位墙拟静力试验

3.2.1试验现象

在加载过程中，构造柱及圈梁均完好，墙体未出现明显的破坏，且绕墙底两端发生转动，如图7（a）所示。实测结果表明，在加载过程中水平滑移很小，其最大值不超过1 mm，表明所采取的墙底构造措施是可靠的，能满足预定要求。加载过程中，金属阻尼器耗能區域发生了明显的变形，如图7（b）所示。

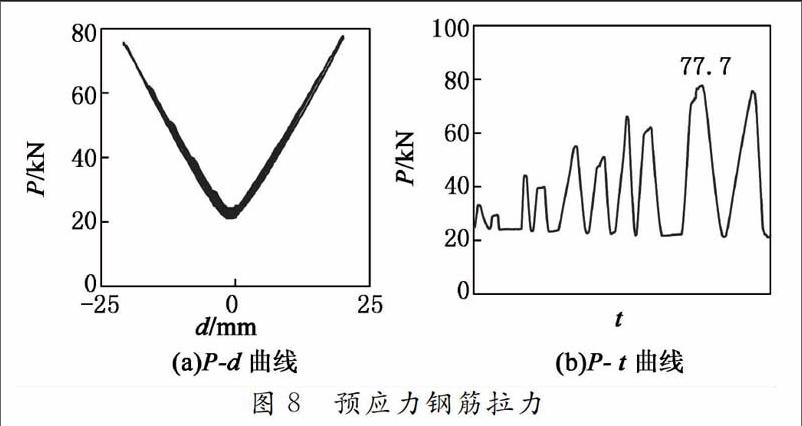
3.2.2预应力筋拉力

考察加载过程中预应力筋拉力最大的工况6。预应力筋拉力P-墙顶水平位移d曲线、拉力P随时间t变化的曲线分别如图8（a）（b）所示。可以看出：1）随着墙体水平位移变大，预应力筋的拉力也逐渐增大。当卸载后，预应力筋的拉力基本回到初始值；2）预应力筋所受的最大拉力为77.7 kN，相应的最大应力为558.9MPa，远小于其强度标准值1 860 MPa，表明预应力筋在加载过程中始终处于弹性状态。

3.2.3滞回曲线

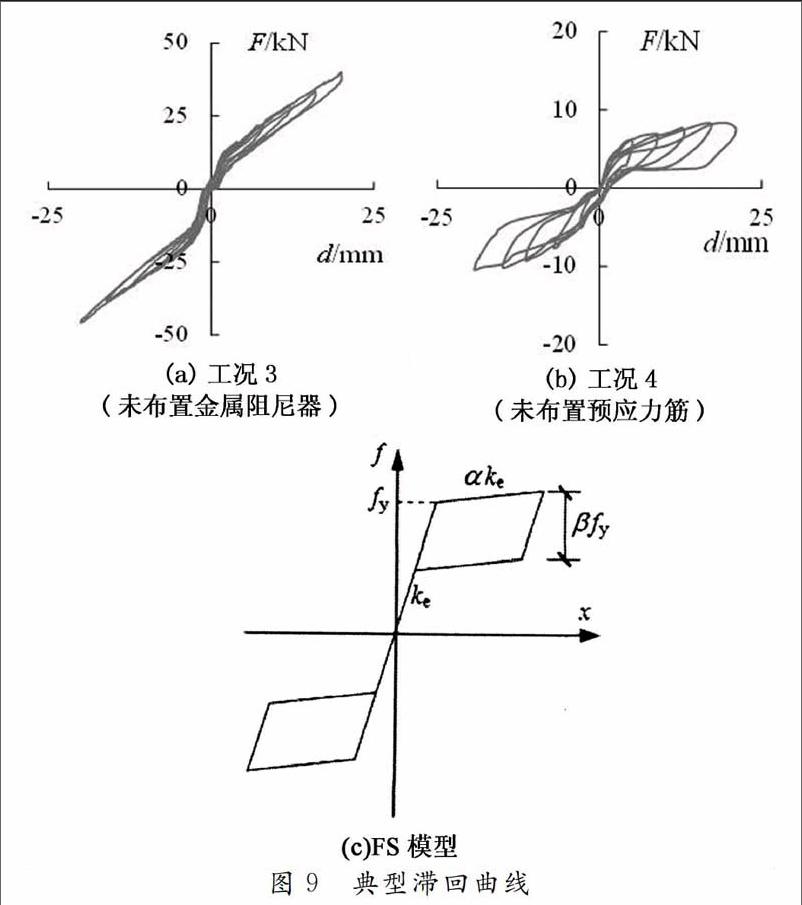
试验所得典型工况下墙顶水平力F_位移d的滞回曲线如图9所示。

可以看出：1）滞回曲线的形状均呈“旗形”，因此可用FS（Flag-shaped）模型来描述其恢复力特性，如图9（c）所示，其中f_y表示屈服荷载，k_e表示弹性刚度，α和β分别表示屈服后的刚度系数及耗能参数；2）滞回曲线加载及卸载没有明显的刚度退化，且卸载后残余变形很小或基本没有，表明本文所提出的新型自复位约束砌体墙具有较好的自复位性能；3）当未布置金属阻尼器时（即工况1～3），自复位墙仍具有一定的耗能能力，其原因在于墙体与基础梁之间可能存在一定的摩擦力而耗能；4）当未布置预应力筋时（即工况1，4，7），墙体卸载后基本上没有残余变形，表明墙体仅通过自重也可基本上实现自复位。

图10所示为预应力筋不同初始预应力对应的滞回曲线。可以看出：1）布置预应筋后，墙体的强度和刚度得到显著提高。尤其对于屈服后刚度，当未布置预应力筋时，墙体屈服后刚度趋近于为0或负值，当布置预应力筋后，墙体屈服后刚度变为正值；2）随着初始预应力的增加，墙体的强度显著增加，但屈服后刚度变化不大；3）随着初始预应力的增加，墙体卸载后残余变形减小，表明增加初始预应力有利于提高墙体的自复位性能。

图11所示为不同阻尼器对应的滞回曲线。可看出：1）布置金属阻尼器后，滞回曲线的形状更饱满，所围成的面积显著增加，表明金属阻尼器可有效地提高自复位约束砌体墙的耗能能力；2）随着阻尼器屈服荷载的增加，滞回曲线所围成的面积变大，表明自复位约束砌体墙的耗能能力增强；3）随着阻尼器屈服荷载的增加，墙体卸载后残余变形变大。

3.2.4等效黏滞阻尼系数

为量化新型自复位约束砌体墙的耗能能力，选取各工况中位移幅值最大的滞回环计算等效黏滞阻尼系数ξ_tq，如下式所示：

（4）式中：E_D，E_S分别表示滞回耗能及最大应变能。

由式（4）计算所得等效黏滞阻尼系数见表2。可看出：1）随着预应力筋初始预应力的增大，ξ_tq减小，表明初始预应力的增加会降低自复位约束砌体墙的耗能能力；2）随着金属阻尼器屈服荷载的增大，ξ_tq增大，表明白复位约束砌体墙的耗能能力增强。

4有限元数值分析模型

4.1数值分析模型的建立

采用OpenSees建立有限元数值分析模型，如图12（a）所示。由试验结果可知，墙体基本上没有明显的损伤，因此采用弹性梁柱单元（elastic BeamColumn）进行模拟。

预应力筋采用桁架单元（Truss element）来模拟，其底端固定于基础，顶端与墙体通过刚性连接件（rigid-link）来模拟，其材料采用Steel02材料进行模拟（即Giuffre-Menegotto-Pinto模型），该材料可以直接施加初始应力来考虑初始预应力。

金属阻尼器采用零长度（zeroLength）单元进行模拟，即通过位于同一位置的2个节点来建模，采用Steel01材料模拟其力位移本构关系，如图12（b）所示，其中E表示弹性刚度，a表示屈服后刚度系数，f_y表示屈服强度。

墙体与基础之间的水平缝用一组只受压弹簧来模拟。与阻尼器相似，采用零长度单元来模拟只受压弹簧，其力位移本构关系选用弹性不能受拉材料（Elastic-No Tension Material），如圖12（c）所示。墙体与阻尼器及只受压弹簧间通过刚性连接件连接。

4.2分析结果对比

采用前节建立的简化数值分析模型，选取2个代表性的工况进行模拟，分别为工况6和9。前者对应于SD-1阻尼器，后者对应于SD-2阻尼器。

将数值分析结果与试验结果进行对比，如图13所示。可以看出：1）从整体上来说，数值模拟结果与试验结果吻合较好，表明所建立的模型具有较高的分析精度，且计算效率很高，可进一步用于数值拓展分析；2）相对于采用SD-1的工况，采用SD-2的工况数值模拟和试验结果相差较大，其原因可能在于金属阻尼器SD-2并没有充分地发挥作用，其连接方式、布置位置等还需要进一步改进。

5结论

本文研制了一种同时布置体内无黏结预应力筋-和外置金属阻尼器的新型自复位约束砌体墙，并通过拟静力试验研究了该新型自复位墙在低周反复荷载作用下的滞回性能，基于试验结果提出了简化的数值分析模型。可以得出如F结论：

1）本文设计的新型自复位约束砌体墙构造措施合理、可靠，达到了预期的目标，其外置式弯曲耗能型金属阻尼器耗能性能稳定。

2）该新型自复位墙在加载过程中未出现明显的损伤，且在加载及卸载过程中没有明显的刚度退化，其滞回曲线呈“旗形”，可用Fs模型近似描述其恢复力特性。

3）布置预应力筋后，墙体的强度和刚度显著提高。随着预应力筋初始预应力的增加，墙体的自复位性能增强，但其耗能能力会降低。

4）布置金属阻尼器后，墙体的耗能能力显著提高。随着金属阻尼器屈服荷载的增大，墙体的耗能能力增强，但会产生少量的残余变形。

5）基于Opensees的新型自复位约束砌体墙简化数值分析模型具有较高的分析精度，且分析效率很高，可进一步用于拓展分析。