考虑残余变形影响的混凝土疲劳损伤本构模型

卫军　李松林　董荣珍　刘晓春　吴志强

摘要：从分析混凝土材料的基本损伤机制出发，考虑疲劳荷载作用下混凝土的损伤累积和残余变形，推导了由Helmholtz自由能表示的混凝土本构方程，根据变分原理建立了基于能量的混凝土疲劳损伤本构模型。并根据疲劳过程中残余变形的发展规律，定义了物理意义明确的残余变形影响因子，并将其与混凝土变形模量损伤因子一同融入混凝土疲劳损伤本构模型中，为混凝土疲劳行为的计算机分析提供了一种更为精确、简化的混凝土疲劳本构模型。试验数据和数值算例的对比误差不超过3%，从而验证了该模型的准确性与适用性。

关键词：混凝土；残余变形影响因子；疲劳行为；疲劳损伤本构模型；模型验证

中图分类号：TU528。01 文献标识码：A

疲劳是指在低于静载强度的循环荷载作用下材料所发生的性能劣化乃至失效。混凝土随着疲劳加载历程的进行，内部微裂缝不断发展，损伤不断积累。研究表明，随着疲劳次数增加，弹性模量不断降低，总变形逐渐增大，其中不可恢复的残余变形部分亦不断增加，这些都是混凝土材料在疲劳过程中非线性行为的显著特征。如何在混凝土疲劳性能研究中全面考虑这些非线性特性，以实现对混凝土及预应力混凝土构件的疲劳性能演变的全过程分析，一直都是研究者和工程界感兴趣的问题。

近年来，有研究者以实际重复加载过程中测量的残余应变和疲劳破坏时极限残余应变之比作为损伤变量建立了疲劳损伤演化方程。有研究者基于疲劳刚度退化、疲劳强度退化与疲劳残余变形演变规律，提出了疲劳累积失效全过程的数值分析方法。有研究者考虑混凝土疲劳过程中残余应变的影响，结合混凝土静力单轴受压本构关系，推导了混凝土疲劳损伤后的等效单轴受压应力应变关系。有研究者根据疲劳等效累积原则和混凝土疲劳残余应变的计算理论，推导出基于残余应变的混凝土疲劳损伤模型。有研究者建立了混凝土棱柱体的非均质细观数值模型，引入弹塑性本构关系，对混凝土的受压性能进行了数值试验，揭示了混凝土的非线性破坏机理。这些研究大大推进了混凝土疲劳非线性分析的研究进程，但现有的模型中有些非线性特性考虑不够简明、具体，大多分析过程较繁琐、费时费力。

为了在混凝土疲劳的计算机分析中更加直观、明确地考虑其非线性特性的影响，亟需构建一种物理意义明确、更为简化的混凝土疲劳本构模型。本文分析了损伤累积和残余变形的影响，定义了具有明确物理意义的残余变形影响因子，结合变形模量损伤因子，建立了基于能量的混凝土疲劳损伤本构模型，试图揭示混凝土的疲劳损伤演变机理及其疲劳受力行为演化规律。

1混凝土疲劳损伤本构模型

1.1疲劳损伤本构模型的构建

由混凝土循环应力应变曲线可以看出混凝土疲劳过程是一个损伤不断累积的过程，此过程也是一个不可逆的热力学过程，如图1所示。

图1中，ε_c（N）为混凝土循环加载N次后的总应变；ε_cr（N）为混凝土循环加载N次后的残余应变；E（N）为混凝土循环加载N次后的弹性模量，E₀为混凝土的初始弹性模量。

混凝土疲劳损伤的过程中，若不考虑热量的耗散，仅考虑等温的纯粹力学过程，混凝土的Helm-holtz自由能ψ为应变ε和损伤变量D的状态函数：

ψ=ψ（ε，D）。 （1）式中：ε为应变；D为损伤变量。

基于热力学的推导可以得到以Helmholtz自由能表示的混凝土材料本构方程基本形式：

（2）

经典的损伤力学认为材料的损伤只与弹性变形有关，然而损伤还造成材料不可恢复的塑性变形，在材料损伤过程中的总应变可以写成弹性应变和塑性应变之和：

ε=ε^e+ε^p。 （3）式中：ε^e为弹性应变；ε^p为塑性应变。

假定弹性与塑性Helmholtz自由能不耦合，因此，疲劳过程混凝土的Helmholtz自由能分解成弹性和塑性两部分：

（4）

若用c（D）代表混凝土N次疲劳损伤后的卸载刚度，那么弹性Helmholtz自由能可以定义为：

（5）

刚度退化由损伤导致，而损伤是不可逆的，因此C（D）为损伤变量D的非递增函数。对于初始无损伤状态C（D）=E₀，那么

（6）

混凝土N次疲劳后的弹性Helmholtz自由能用损伤变量表示：

（7）

由式（2）可得：

（8）

将式（3）和（7）代入式（8）得混凝土的受压损伤本构模型：

（9）式中：ε^p为塑性变形，疲劳荷载作用下为残余变形ecr。

于是混凝土的疲劳损伤本构模型为：

（10）式中：σ_c（n）≤σ₀，σ₀為初始加载时的应力值；ε_c（N）为循环荷载作用N次后的峰值应变。ε_cr（N）为循环荷载作用N次后的残余应变。

式（10）即为混凝土的疲劳损伤本构模型，能很好地考虑混凝土在疲劳荷载作用下的损伤累积和残余变形等非线性因素。

1.2模型参数的确定

1.2.1变形模量损伤因子

式（10）确定了混凝土的疲劳损伤本构模型，下面对模型中参数的具体取值进行简化和确定。

D（N）为考虑混凝土疲劳过程刚度衰减的变形模量损伤因子：

（11）

1.2.2残余变形影响因子

根据文献的试验结果，混凝土在疲劳过程中的残余应变和最大应变具有相同的三阶段发展规律，其比值能很好地反映混凝土在疲劳过程的变形特征，将其比值定义为混凝土疲劳残余变形影响因子，即：

（12）式中：ε_cr（N）为循环荷载作用N次后的残余应变；ε_c（N）为循环荷载作用N次后的总应变。

将式（11）和（12）代入式（10）得到：

（13）

式（13）即为混凝土疲劳损伤本构模型，在残余变形影响因子确定的情况下，结合变形模量损伤因子，即可得到混凝土塑性损伤本构模型。该模型能够全面考虑混凝土残余变形和刚度退化对混凝土疲劳受力行为的影响，物理意义明确，可以方便地用于混凝土疲劳全过程的计算机分析。

2模型验证

2.1试验验证

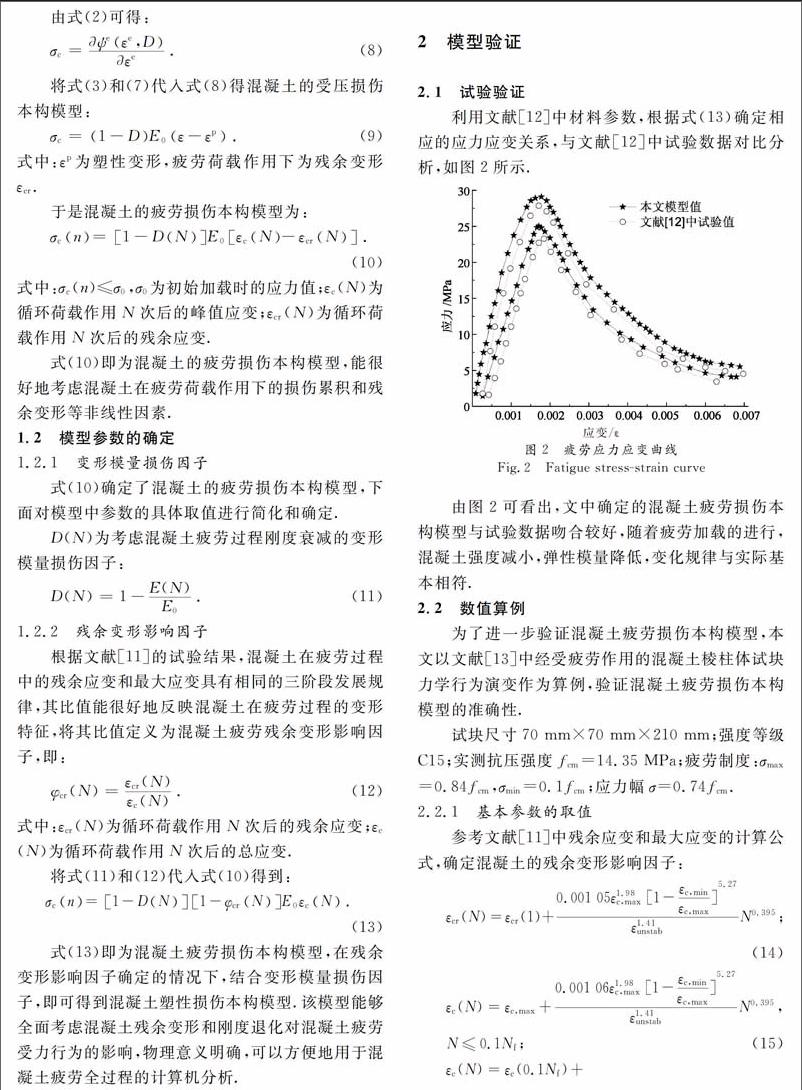
利用文献中材料参数，根据式（13）确定相应的应力应变关系，与文献中试验数据对比分析，如图2所示。

由图2可看出，文中确定的混凝土疲劳损伤本构模型与试验数据吻合较好，随着疲劳加载的进行，混凝土强度减小，弹性模量降低，变化规律与实际基本相符。

2.2数值算例

为了进一步验证混凝土疲劳损伤本构模型，本文以文献中经受疲劳作用的混凝土棱柱体试块力学行为演变作为算例，验证混凝土疲劳损伤本构模型的准确性。

试块尺寸70 mm×70 mm×210 1Tim；强度等级C15；实测抗压强度f_cm=14.35 MPa；疲劳制度：σ_max=0.84f_cm，σ_min=0.1f_cm；应力幅σ=0074f_cm。

2.2.1基本参数的取值

参考文献中残余应变和最大应变的计算公式，确定混凝土的残余变形影响因子：

（14）

（15）

（16）式中：ε_c，max，ε_c，min分别为循环荷载的上下限对应的瞬时应变；ε_cr（1）为应力循环第一次的残余应变；ε_unstab为疲劳变形第三阶段开始时混凝土的纵向总变形。

参照大量研究结果，认为混凝土第三阶段开始时混凝土的纵向总变形ε_unstab与疲劳荷载应力幅和疲劳次数无关，只取决于混凝土材料的性质。取混凝土一次加载破坏时峰值应力对应的应变为ε₀。

考虑ε_cr（1）为第一次加载卸载的残余应变，参考文献取ε_cr（1）=0；

将式（14）（15）（16）代入式（12）计算残余变形影响因子；

参考文献，考虑混凝土强度等级的影响，按下式确定D（N）。

（17）

选用ABAQUS的C3D8R单元，网格为5 mm，采用式（13）定义的混凝土疲劳损伤本构关系，按照式（18）规定的混凝土累积损伤的破坏准则，进行建模分析。

（18）

2.2.2结果分析

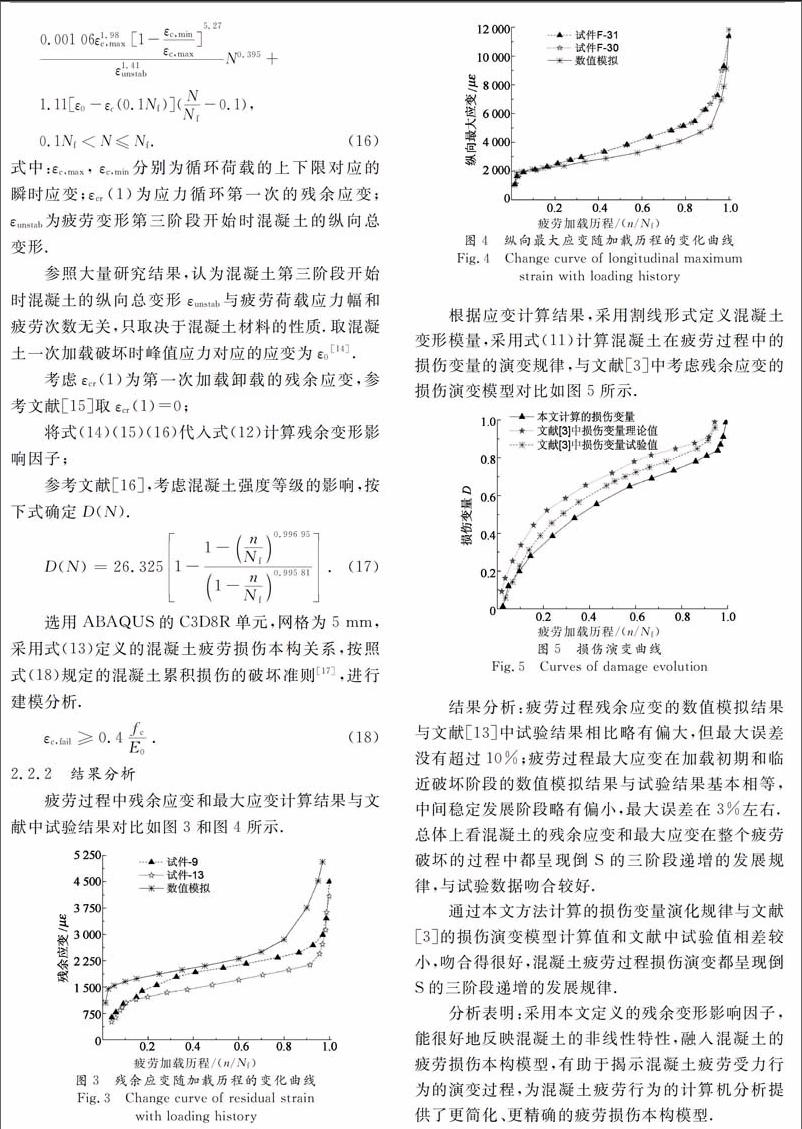
疲劳过程中残余应变和最大应变计算结果与文献中试验结果对比如图3和图4所示。

根據应变计算结果，采用割线形式定义混凝土变形模量，采用式（11）计算混凝土在疲劳过程中的损伤变量的演变规律，与文献中考虑残余应变的损伤演变模型对比如图5所示。

结果分析：疲劳过程残余应变的数值模拟结果与文献中试验结果相比略有偏大，但最大误差没有超过10%；疲劳过程最大应变在加载初期和临近破坏阶段的数值模拟结果与试验结果基本相等，中间稳定发展阶段略有偏小，最大误差在3%左右。总体上看混凝土的残余应变和最大应变在整个疲劳破坏的过程中都呈现倒S的三阶段递增的发展规律，与试验数据吻合较好。

通过本文方法计算的损伤变量演化规律与文献的损伤演变模型计算值和文献中试验值相差较小，吻合得很好，混凝土疲劳过程损伤演变都呈现倒S的三阶段递增的发展规律。

分析表明：采用本文定义的残余变形影响因子，能很好地反映混凝土的非线性特性，融入混凝土的疲劳损伤本构模型，有助于揭示混凝土疲劳受力行为的演变过程，为混凝土疲劳行为的计算机分析提供了更简化、更精确的疲劳损伤本构模型。

3结论

1）本文定义的残余变形影响因子，其物理意义明确，形式简单，能够准确地反映混凝土疲劳非线性特性和受力行为的演变过程。

2）将残余变形影响因子作为参数，结合变形模量损伤因子，能够简单直接地应用于混凝土损伤本构模型，得到形式简单、物理意义明确的混凝土疲劳损伤本构模型。

3）算例表明：考虑残余变形影响因子和变形模量损伤因子的混凝土疲劳损伤本构模型能够全面反映混凝土疲劳非线性特性，准确、便捷地用于混凝土疲劳受力行为分析，误差在3%左右。

本文仅在等幅疲劳应力下研究混凝土疲劳损伤本构模型，考虑加载频率以及变幅应力的影响将在进一步的研究中展开。