川西马井气田蓬莱镇组致密砂岩储层可动水饱和度计算方法

司马立强, 王超, 吴丰, 王亮, 马力, 王紫娟

(1.西南石油大学地球科学与技术学院, 四川 成都 610500; 2.中国石油川庆钻探工程有限公司测井公司, 重庆 400021; 3.西安昌源石油科技服务有限责任公司, 陕西 西安 710076)

0 引 言

可动水饱和度是储层测井评价的重要参数[1],也是储层流体性质识别、产能预测、开发方案制定的参考依据。常规砂岩储层中,可动水饱和度可通过岩石总含水饱和度与束缚水饱和度的差值确定[2]。然而,与常规砂岩储层相比,致密砂岩储层受复杂岩性、超低孔隙度渗透率、复杂孔隙结构等因素的影响,储层岩电参数之间表现出明显的非阿尔奇现象[3-6],常规的阿尔奇公式难以表征储层的导电特性,准确计算储层的含水饱和度。现有的建立在常规砂岩储层中的束缚水饱和度模型在复杂孔隙结构的致密砂岩储层中应用效果较差[7-8]。

针对复杂储层岩电关系呈现的非阿尔奇现象,前人开展了大量的研究[9-16]。国外学者Raiga-Clemenceau与Fraisse认为泥质砂岩的总电导率是泥质部分的电导率与岩石部分的电导率之和[9];Givens与Schmidt提出了一种考虑岩石骨架的电阻率模型[10-11];Crane提出了具有一般意义的扩展阿尔奇定律[12]。中国学者李舟波等在传统体积模型的基础上提出了三水模型,即将岩石总电导视为自由水、微孔隙水、黏土水3部分的并联[13];黄布宙基于三水模型提出了一种三孔隙混合导电体积模型[14];李霞等对低孔隙度、低渗透率碎屑岩储层岩石导电机理的研究认为不同孔隙类型是影响岩石导电的关键,进而提出岩石导电以大孔隙和微孔隙中流体为主的双孔隙导电体积模型[15],但未能提出模型中微孔(束缚)孔隙度这一关键参数的测井评价方法,使得该模型在实际应用中受到限制;王明方研究双孔隙组分模型在低渗透储层的适用性中,也未能对该方法中的束缚孔隙度参数进行研究[16]。文献显示,描述储层岩石导电特性,进而评价储层含水饱和度的模型较多,但是,针对不同的储层特征,其适应效果存在差异。

本文针对川西蓬莱镇组气藏致密砂岩储层的可动水饱和度评价开展储层特征分析,明确影响储层岩石导电特性的主控因素。选取基于复杂孔隙结构的双孔隙导电体积模型对该地区砂岩储层饱和度进行研究,确定致密砂岩储层可动水饱和度的模型,并对模型中的几个关键参数进行了分析。

1 储层特征

川西蓬莱镇组致密砂岩储层气藏位于川西凹陷,气藏平面类型多样,主要为构造及岩性双重控制下的高压、异常高压气藏。薄片资料显示,储层碎屑组分主要由石英、长石和岩屑组成,孔隙类型以粒间孔为主,含少量粒内溶孔;储层岩心样品孔隙结构差异较大,不同类型的岩样孔隙间的连通性明显不同;岩石颗粒表面存在少量泥质;储层孔隙度主要分布在2.82%～15.26%,平均孔隙度为8.66%;渗透率主要分布在(0.001～0.919)×10-3μm2,平均渗透率为0.125×10-3μm2;压汞资料表明,孔喉半径较小,在0.004～1 μm,表现为明显的双峰态分布特征;渗透率主要由0.25～1.6 μm的孔喉所贡献(见图1)。综上所述,川西致密砂岩储层物性较差,属于低孔隙度、低渗透率储层,孔隙结构复杂。常规求取中、高孔隙度渗透率储层的饱和度计算方法研究该类储层水可动性适用性不强,误差较大。

图1 致密砂岩储层铸体薄片以及压汞孔喉分布图

2 基于双孔隙模型求取可动水饱和度

2.1 致密砂岩导电模型的选取

分析研究区9块岩心的岩电数据发现,微孔隙发育的岩心I—Sw关系均存在明显的非阿尔奇现象,常规的阿尔奇模型无法准确描述该类储层的非阿尔奇现象。李舟波等提出的三水模型以及李霞等提出的双孔隙导电体积模型均能较好地描述这种岩电关系特征[13,15]。由于三水模型涉及参数较多,其实用性较差。储层特征分析显示蓬莱镇组致密砂岩储层孔隙结构表现为明显的双峰态,且泥质含量较少。储层的这些特征满足双孔隙导电体积模型的假设条件,为此选取双孔隙导电体积模型研究储层的I—Sw的非线性变化关系,以孔隙发育不同的I号岩心和II号岩心为例(岩心物性参数见表1),利用阿尔奇模型和双孔隙导电体积模型分别对岩心的I—Sw关系进行研究。

图2 I号岩心与II号岩心I—Sw关系对比图

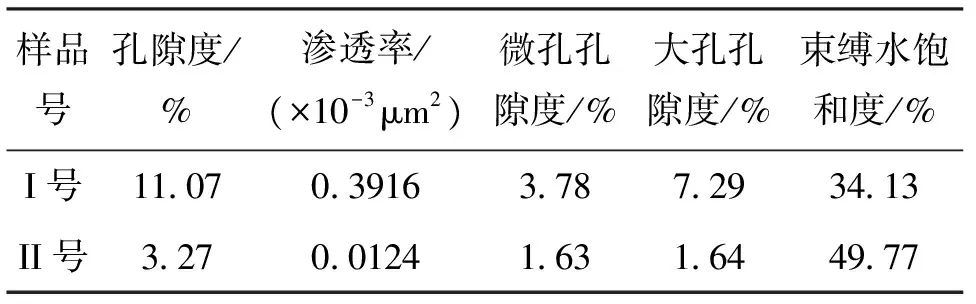
表1 I号岩心与II号岩心物性参数值

结果显示,大孔隙发育的I号岩心,阿尔奇模型与双孔隙导电体积模型均能较好描述岩心岩电关系特征[见图2(a)];微孔隙发育的II号岩心,随着含水饱和度的降低,I—Sw呈现出非线性的变化趋势,即非阿尔奇特征明显[见图2(b)]。对于微孔隙较发育的致密砂岩储层与常规阿尔奇模型相比,双孔隙导电体积模型能够较准确地表征岩石的岩电关系特征。

2.2 基于双孔隙体积模型的可动水饱和度计算

双孔隙导电体积模型将孔隙分为大孔隙和微孔隙。微孔隙中的水不可动,油气等不能进入微孔隙;大孔隙中的水可动,油气可进入大孔隙。双孔隙体积导电模型数学表达式为

(1)

式中,φf为大孔(可动)孔隙度,%;φb为微孔(束缚)孔隙度,%;mf为大孔胶结指数;mb为微孔胶结指数;n为饱和度指数;Rw为地层水电阻率,Ω·m;Rt为地层真电阻率,Ω·m;Swf为大孔中的含水饱和度,%;Swb为微孔中的含水饱和度,%;nb为微孔的饱和度指数。

双孔隙导电体积模型中

(2)

将式(2)带入式(1)得到大孔隙中的含水饱和度Swf

(3)

储层中可动水饱和度可表示为

(4)

式(4)中,总孔隙度φ可以通过三孔隙度测井获得,Rw可通过地层水分析资料获得。要准确求取Swm,模型中mf、mb、n以及φb、φf等参数的求取是关键(其中,φf=φ-φb)。

2.3 模型参数的求取

2.3.1mf、mb等参数的计算方法

将研究区9块岩心的岩电实验数据进行非线性多参数拟合求最优解,得到该地区每块岩心对应的大孔隙胶结指数mf、微孔隙胶结指数mb以及饱和度指数n值。由于不同岩心孔隙结构不同,所得各参数值存在差异。分析发现,岩心的mf、mb值与总孔隙度φ相关性较好,两者相关系数均较高(见图3);相同类型孔隙结构的岩心n值近似相等,使用时取n的平均值。

2.3.2 束缚孔隙度计算的新方法

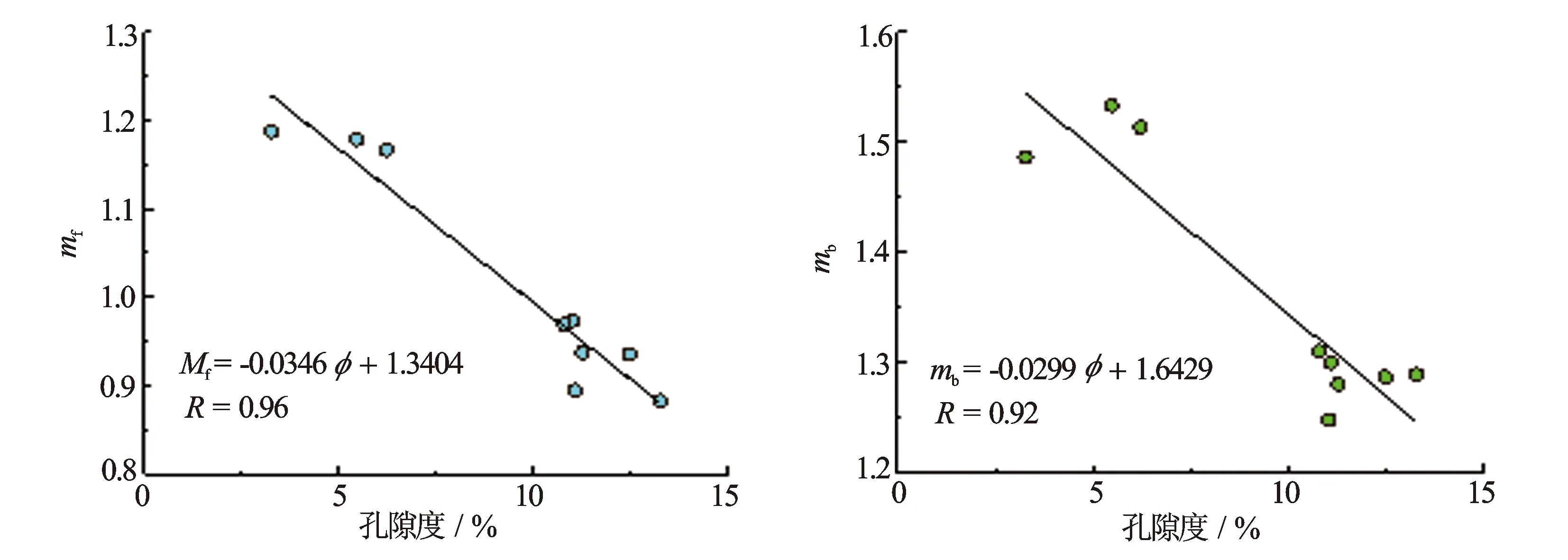
图3 孔隙度φ与mf、mb关系图

图4 2种模型计算Swir值与核磁共振实验值交会图

模型中束缚孔隙度φb可通过储层束缚水饱和度求取,即φb=φSwir。但是,川西蓬莱镇储层属于低孔隙度、低渗透率储层,具有复杂的孔隙结构,准确求取束缚水饱和度难度较大,而实验求取束缚水饱和度方法由于取心数量有限、实验测试成本过高,在油气田实际应用中存在一定局限性。谭海芳等[18-20]认为对于某个特定地区,可选择利用孔隙度建立束缚水饱和度模型;陈科贵等[8]认为致密砂岩储层束缚水饱和度受到复杂孔隙结构的影响,可利用束缚水饱和度和孔隙结构指数之间的关系建立束缚水饱和度模型。针对川西某气藏蓬莱镇组致密砂岩储层,分别尝试采用孔隙度、孔隙结构指数与核磁共振测试束缚水饱和度建立束缚水饱和度模型[见式(5)、式(6)]求取储层束缚水饱和度。结果表明,孔隙度与束缚水饱和度的相关性差,相关系数R=0.44;孔隙结构指数与束缚水饱和度相关性较高,相关系数R=0.78。

Swir=-0.015φ+0.843

(5)

Swir=-0.045ln (K/φ)+0.453

(6)

分别将2种模型计算的束缚水饱和度与核磁共振测试的束缚水饱和度进行对比(见图4),结果表明,基于孔隙度计算的束缚水饱和度和核磁共振测试的束缚水饱和度二者平均绝对误差10.12%;基于孔隙结构指数计算的束缚水饱和度和核磁共振测试的束缚水饱和度二者平均绝对误差6.85%,但大多数点的分布仍然偏离45°线。分析发现,束缚水饱和度除了受孔隙结构的影响,也受到粒度中值、泥质含量的影响,使得上述2种方法求取束缚水饱和度效果较差。因此,在建立束缚水饱和度模型时应当考虑粒度中值、泥质含量的影响。

常规测井分析中,泥质含量Vsh的求取可通过自然伽马值计算;粒度中值Md曲线的变化与自然伽马曲线的变化存在明显的相关性[21],因此,粒度中值的求取可通过自然伽马值计算

lgMd=C0+C1ΔGR

(7)

式中,C0、C1为经验系数;ΔGR为自然伽马相对值。

(8)

结合常规测井数据以及核磁共振测试束缚水饱和度,利用统计回归方法求取新模型中的系数

(9)

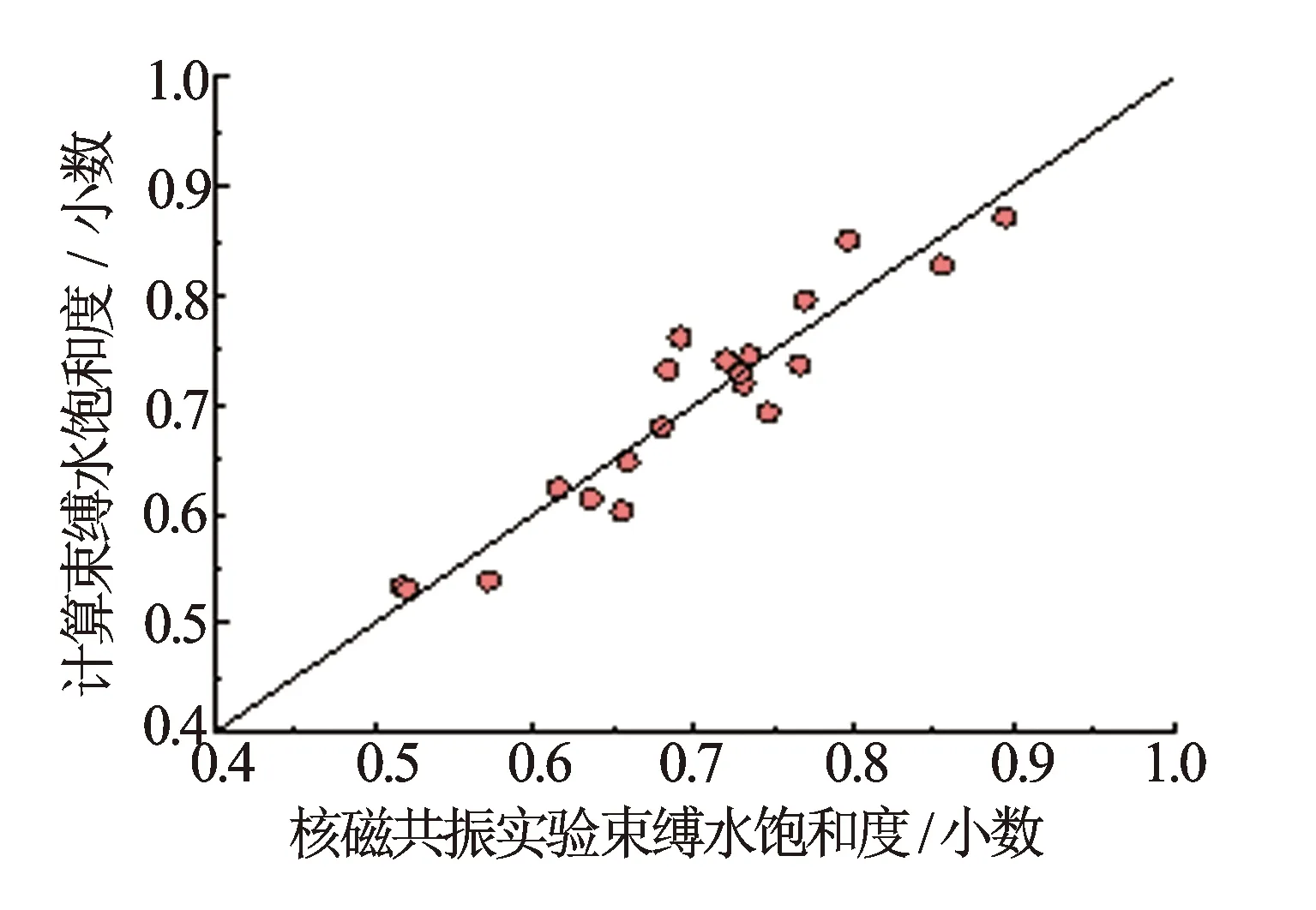
图5 束缚水饱和度计算值与核磁共振实验值交会图

3 可动水饱和度计算方法的应用

针对川西某气藏蓬莱镇组储层是否产水,以S2井为例,利用双孔隙导电模型可动水饱和度计算方法及建立的束缚水饱和度模型对该井储层水可动性进行分析(见图6)。经计算,射孔层段1 179～1 185 m处平均束缚水饱和度为50.47%,平均可动水饱和度为2.65%,可动水饱和度较小,综合解释为气层;而利用常规阿尔奇模型求取的含水饱和度和束缚水饱和度值二者确定的平均可动水饱和度为8.78%。对比试油气结果,产气10 001 m3/d,产水0 m3/d。利用双孔隙导电模型可动水饱和度计算方法得到的解释结论与试油气结果更符合。应用双孔隙导电模型可动水饱和度计算方法分析处理了20多口井,对比试油气结果,解释符合率达到80%以上。

图6 S2井测井解释成果图*非法定计量单位,1 ft=12 in=0.304 8 m,下同

4 结 论

(1) 致密砂岩储层岩电关系存在明显的非阿尔奇现象,可以使用基于双孔隙导电体积模型计算储层可动水饱和度。此外,双孔隙导电体积模型中参数mf、mb与测井孔隙度相关性较好,可利用测井计算孔隙度直接求取,饱和度指数n值在特定地区变化不大,计算中可使用n的平均值。

(2) 考虑到致密砂岩储层束缚水饱和度受储层孔隙度、孔隙结构、黏土含量、粒度中值等因素的影响,提出了更加适用于川西地区蓬莱镇储层的新型束缚水饱和度模型。新建立的束缚水饱和度模型平均绝对误差最小,精度更高。

(3) 利用基于双孔隙导电模型的可动水饱和度计算方法,结合新型的参数求取方法,在具有复杂孔隙结构的致密砂岩储层适用性较好,提高了储层可动水饱和度解释精度,能较好地描述储层水的可动性并对产水特征进行准确分析。

参考文献:

[1] 叶礼友, 高树生, 熊伟, 等. 可动水饱和度作为低渗砂岩气藏储层评价参数的论证 [J]. 石油天然气学报, 2011, 33(1): 57-59.

[2] 黄伟岗, 郭平, 姜怡伟, 等. 桥白气藏可动水实验研究 [J]. 天然气勘探与开发, 2005, 28(2): 39-42.

[3] 孙小平, 石玉江, 姜英昆. 复杂孔隙结构储层含气饱和度评价方法 [J]. 天然气工业, 2000, 20(3): 4144.

[4] 王黎, 孙宝佃, 沈爱新, 等. 某油田低孔隙度低渗透率泥质砂岩储层岩电实验及应用 [J]. 测井技术, 2005, 29(2): 91-94.

[5] 张明禄, 石玉江. 复杂孔隙结构砂岩储层岩电参数研究 [J]. 测井技术, 2005, 29(5): 446-448.

[6] 石玉江, 李高仁, 周金昱. 泥质型低渗砂岩储层岩电性质研究及饱和度模型的建立 [J]. 测井技术, 2008, 32(3): 203-206.

[7] 付晨东. 用核磁共振测井资料确定束缚水饱和度的新方法 [J]. 测井技术, 2011, 35(3): 243-246, 253.

[8] 陈科贵, 温易娜, 何太洪, 等. 低孔低渗致密砂岩气藏束缚水饱和度模型建立及应用——以苏里格气田某区块山西组致密砂岩储层为例 [J]. 天然气地球科学, 2014, 25(2): 273-277.

[9] RAIGA-CLEMENCEAU J, FRAISSE C, GROSJEAN Y. The Dual-porosity Model, a Newly Developed Interpretation Method for Shaly Sands [C]∥SPWLA, 25th Annual Logging Symposium, Paris, France, 1984.

[10] GIVENS W W. Formation Factor, Resistivity Index and Related Equations Based upon a Conductive Rock Matrix Model(CRMM) [C]∥SPWLA, 27th Annual Logging Symposium, Dallas, Texas, 1986.

[11] GIVENS W W, SCHMIDTE J. A Generic Electrical Conduction Model for Low-contrast Resistivity Sandstone [C]∥SPWLA, 29th Annual Logging Symposium, Dallas, Texas, 1988.

[12] CRANE S D. IMPACTS of Microporosity, Rough Pore Surface and Conductive Minerals on Saturation Calculations from Electric Measurements: An Extended Archie’s Law [C]∥SPWLA 31st Annual Logging Symposium, Lafayette, Louisiana, 1990.

[13] LI Z B, MO X W. Study on Electric Property of Shaly Sand and Its Interpretation Method [J]. Jounal of Geoscientific Research in Northeast Asia, 1999, 2(1): 110-114.

[14] 黄布宙. 泥质砂岩三孔混合导电模型及应用 [D]. 长春: 吉林大学, 2005.

[15] 李霞, 赵文智, 周灿灿, 等. 低孔低渗碎屑岩储集层双孔隙饱和度模型 [J]. 石油勘探与开发, 2012, 39(1): 82-91.

[16] 王明方. 低渗透储层孔隙结构评价方法研究——以以南堡油田东营组二段和三段为例 [D]. 东营: 中国石油大学(华东), 2012.

[17] 赵毅, 胡斌, 张路崎, 等. 基于核磁共振和压汞实验的储层束缚水饱和度计算方法 [J]. 科技导报, 2010, 28(11): 64-67.

[18] 谭海芳, 黄书坤. 确定束缚水饱和度的方法研究 [J]. 国外测井技术, 2006, 21(4): 23-24.

[19] 高华, 高楚桥, 胡向阳. 莺歌海盆地束缚水饱和度影响因素研究 [J]. 石油物探, 2005, 44(2): 158-159.

[20] 李宁, 周克明, 张清秀, 等. 束缚水饱和度实验研究 [J]. 天然气工业, 2002, 22(增刊): 110-113.

[21] 洪有密. 测井原理与综合解释 [M]. 东营: 中国石油大学出版社, 2004.