基于有限体积法的致密油储层数字岩心中流动与传热研究

李昂, 于浩波, 谢斌, 黄波, 冯耀荣, 宫敬, 郝鹏飞

(1.中国石油大学(北京)油气管道输送安全国家工程实验室, 北京 102249; 2.大庆油田采油工程研究院, 黑龙江 大庆 163453; 3.中国石油新疆油田工程技术研究院, 新疆 克拉玛依 834000; 4.清华大学航天航空学院, 北京 100084)

0 引 言

致密油藏由于其储量可观,开发潜力大,20世纪中期在国外已经受到重视并开采,取得了巨大成功,如窦宏恩等[1]介绍的美国巴肯油藏。在微尺度下研究致密油储层的孔隙结构及流体在其中的传热传质对于储层的高效开发及环保领域有着重要意义[2-3]。

致密储层岩心属于结构复杂的多孔介质,研究流体在其中的流动首先要获取其内部的三维空间结构,然后才能进行流动模拟。中国学者对国外研究成果进行了总结对比后均指出,使用X射线对样品进行CT扫描建立数字岩心是一种准确而有效的获取岩心内部空间结构的手段[4-6]。

对孔隙中的微观流动进行数值模拟是近年国内外学者研究的热点,对于其模拟方法有基于孔隙网络模型法(PNM)[7]、格子Boltzmann法(LBM)[8-11]及计算流体力学(CFD)方法[12-18]。PNM方法,在简化模型的基础上进行流动模拟,得出的结果很可能与实际状况产生较大误差[12]。LBM方法,虽然能够处理复杂的边界条件,编程简单,但是运算量巨大,计算耗时长[13]。运用CFD方法是孔隙流动模拟的发展趋势。当前的研究成果主要集中在孔隙中的流动上,还很少有涉及到其中传热问题的研究,而Wu M等[19]与Yang L等[20]指出研究其中的传热状态也很有必要,而且其研究对象主要是孔隙度较高、渗透率较大的岩心模型,比如Berea、Fontainebleau砂岩模型以及Sandpack填充模型等。关于低渗透率的致密岩心(渗透率<1.0×10-3μm2)的研究还很少。

本文选取低渗透率致密岩心作为研究样品,结合Micro-CT扫描与后续图像处理及网格划分技术,使用基于有限体积法(FVM)的CFD软件ANSYS FLUENT计算岩心的速度与温度分布状况,为研究岩心类多孔介质中的流动与传热问题提供一种新方法。

1 岩心三维模型的建立

CT扫描是利用穿透性好的X光拍摄岩心不同角度的透射图像,再利用层析成像算法反演出每个成像点的透射率值,该值大小直接反映出该点的物质密度;以白色表示高密度物质,以黑色表示孔隙,形成灰度图像。

本文中使用ZEISS公司生产的Versa510对样品进行成像,该设备最高分辨率为300 nm。岩心样品来自新疆油田吉木萨尔31号井,为白云质岩,在样品中钻取直径约1 mm圆柱进行扫描实验,可以获得分辨率为916×994的二维灰度图像970张[见图1(a)],空间分辨率为1 μm/像素。在二维灰度图像中可以清楚地看到,黑色的部分为孔隙(低密度),灰白色的部分为骨架(高密度)。通过二维图像的叠加可以得到样品的三维灰度图像。将所有图像用于重建数字岩心对计算机的性能有非常高的要求,本研究中使用Mostaghimi P等计算出的数字岩心的代表元体积(REV)来确定重构区域尺寸[15],即从图像中选取体积为200 μm×200 μm×200 μm的区域作为研究对象。图像处理在三维可视化软件AVIZO中进行。

图1 CT扫描实验说明

使用Micro-CT扫描获得的灰度图像存在各类噪声,会对结果产生影响。进行图像处理之前首先需要对灰度图像进行降噪。研究中使用降噪效果比较好的中值滤波法对原始图像进行降噪;之后对二维灰度图像进行阈值分割,根据灰度值的差异将孔隙空间与岩石骨架区分开,图1(b)为阈值分割后二维切片图。将阈值分割后的图像从下往上叠加,再使用Marching Cubes算法产生三维孔隙表面,去除孤立孔隙后通过提取孔隙结构的中心线建立起表征孔隙空间简化结构的网络模型,三维重构结果以及孔隙网络模型见图2。

岩心的三维重构结果可以直观地看出孔隙的分布状况,但是要深入认识孔隙结构的特点还需要对其特征参数进行统计分析。首先在重建模型中使用的快速分水岭算法将每个孔隙进行标记,所有孔隙的体积和等效直径便可以统计出来,再除以重构区域体积便可以算出重建模型孔隙度大小为8.34%。与实测孔隙度8.73%比对发现,计算孔隙度稍小于实测孔隙度,可能原因为在图像处理中将一部分小的孤立孔隙去除所导致,岩心的非均质性也可能会造成计算值与实测值存在一些误差[12]。孔隙喉道的直径及体积的分布见图3。

图2 数字岩心构建结果

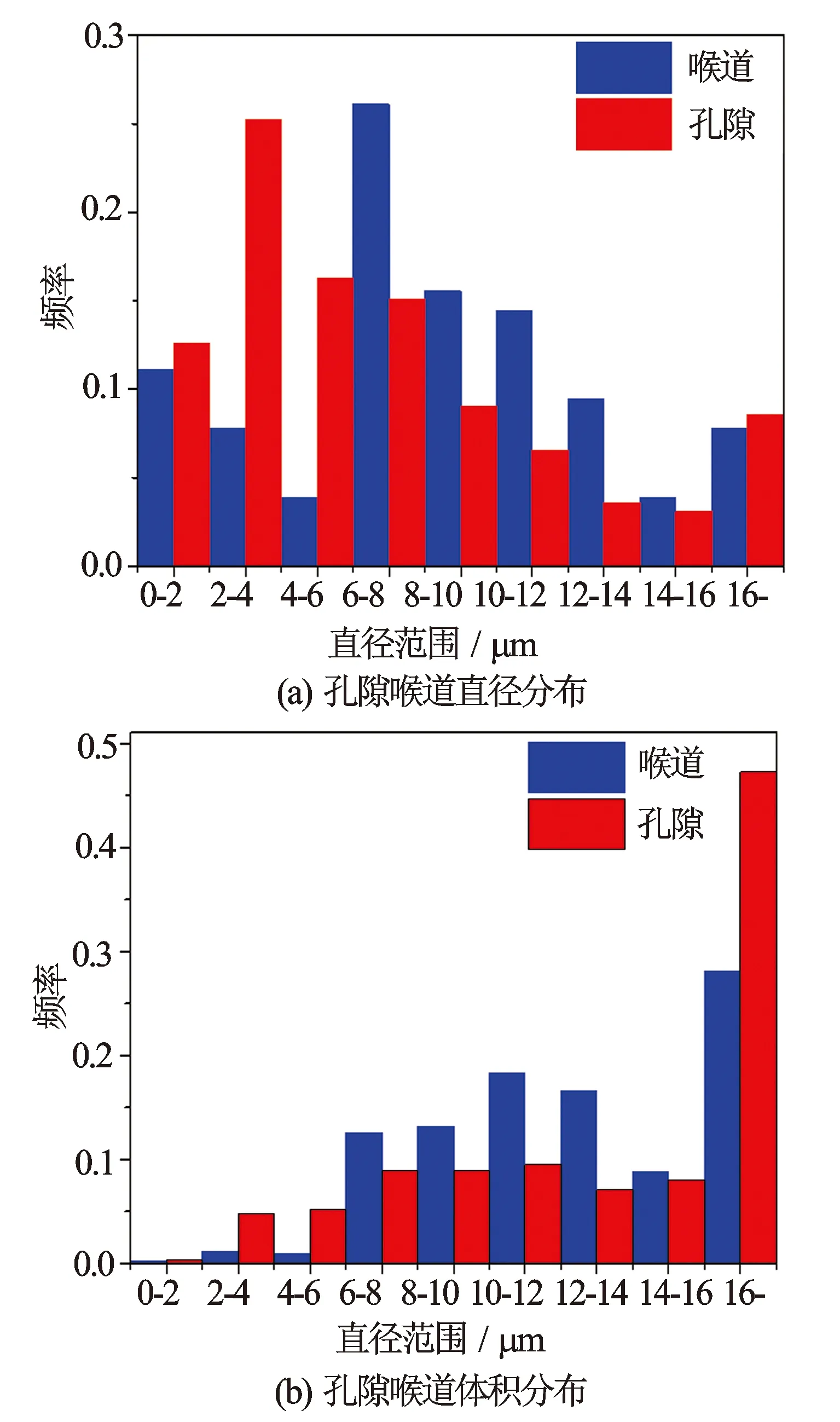
图3 孔隙喉道直径与体积分布

2 计算过程

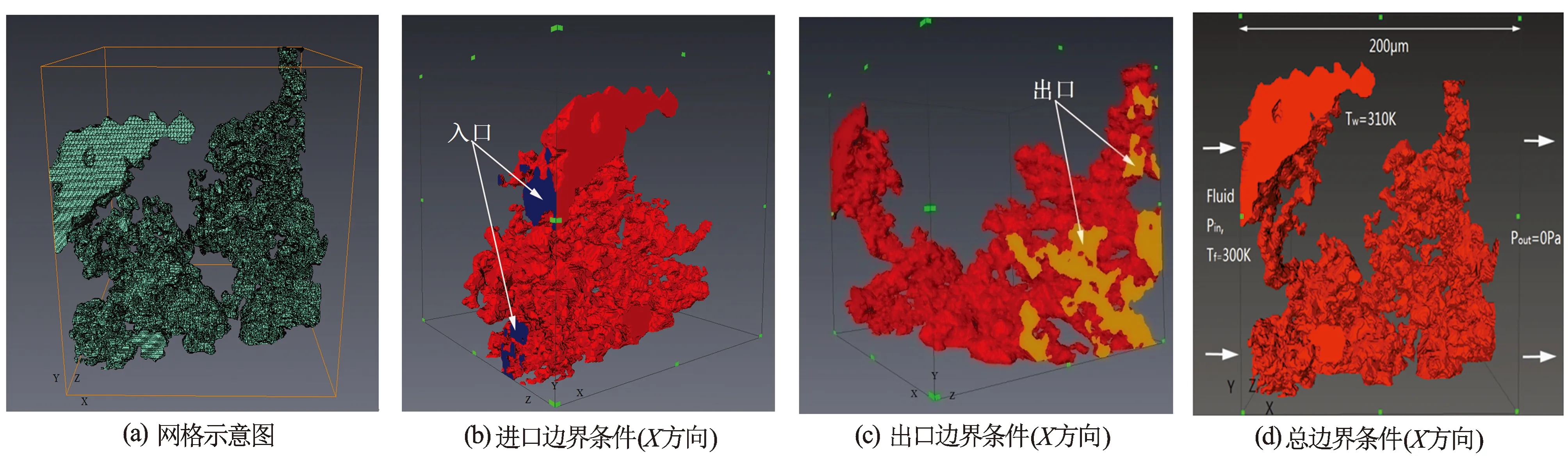
图4 网格及边界条件

CFD计算方法主要包括有限差分法(FDM)、有限元法(FEM)以及有限体积法(FVM)。其中,FVM是最为普遍的一种数值计算方法,计算结果准确且适用于复杂几何结构,通用性较广的CFD软件中大多都采用该方法[21],然而该种方法在孔隙级的流动模拟中使用却很少。为此,需搭建重构模型与基于FVM的计算软件ANSYS FLUENT对接的桥梁。

首先对几何模型进行网格划分,该步骤在AVIZO软件中的Generate Tera Grid模块中进行。在产生网格之前,必须先对重构数字岩心进行表面处理,去除孔隙空间表面交叉的部分并保持几何模型的闭合性,使之能够产生网格,经表面处理后产生的网格数约为537万个;在网格产生后还需要对产生的非结构化四面体网格进行优化,以免在后续迭代计算过程中出现不收敛或者运算超出浮点数。研究以X、Y、Z这3个坐标轴为流动方向进行计算,不同流动方向进出口边界条件亦不同,需要分别设置,如图4所示(以X轴流动方向为例),其中图4(b)中的紫色平面和图4(c)中的金黄色平面分别为流体的进口和出口。计算时进口压力分别设置为10 Pa,出口压力设置为0 Pa,流体设置为液态水,进口温度设为300 K,壁面温度设置为310 K,边界条件如图4(d)(以X轴流动方向为例)。由于流体在孔隙中的流速较低,故在计算前假设其中的流动为层流状态,即低雷诺数Stokes流,且壁面无滑移,其流动控制方程为

·V=0

(1)

μ2V-p=0

(2)

式中,V为流体在多孔介质中的速度矢量;μ为流体动力黏度;为拉普拉斯算子;p为多孔介质中流体的压力。温度场则通过求解能量方程得出。

经过求解器的迭代计算,在一定压差下水通过岩心孔隙空间的体积流量的数值解便可以求解出来,并使用达西定律计算出绝对渗透率。在达西定律中,绝对渗透率视为常数,只与孔隙的几何形状有关,是岩石本身的性质,与通过的流体性质无关。达西定律的表达形式为

(3)

式中,Q为通过多孔介质的流体的体积流量,μm3/s;S为流体流动方向上样品的截面积,μm2;K为绝对渗透率,μm2;μ为流体的动力黏度,Pa·s;Δp为多孔介质两侧压差,Pa;L为流动方向上样品的长度,μm;Q/S为通过多孔介质的渗流速度,即达西速度。

图5 三维渗流流线图

3 计算结果及分析

3.1 绝对渗透率计算结果

重构区域内的3个不同方向的绝对渗透率数值计算结果与实测渗透率见表1。从渗透率实测值可知实验岩心属于白云质岩中渗透率较高的样品;同时每个流动方向的渗透率都互不相同,且理论值与实验结果相比存在一些误差,杜新龙[12]提出这种误差是受到岩心的非均质性以及扫描的分辨率等影响所致,但理论计算结果与实验值均在同一数量级并且已较为接近,对于孔隙级别的流动来说该误差在可以接受的范围内。与用有限元软件COMSOL来计算的方法相比,虽然使用COMSOL计算得到的结果非常接近,但是使用ANSYS FLUENT进行迭代计算时收敛速度更快,在同一台计算机上达到相同计算精度的时间只需要COMSOL的1/5左右,在孔隙级别流动模拟计算中使用ANSYS FLUENT进行计算更有优势。

表1 岩心渗透率计算结果

3.2 渗流流场分析

将计算所得数据进行后处理作出的三维流线图见图5所示。从流线图5可以直观地观测到流体在孔隙内部的分布状况,有流线穿过的区域表明该区域有流体流动,流线颜色靠近红色表示该处流速越快,越靠近蓝色则表示流速越慢。

之前算出X、Y、Z这3个流动方向绝对渗透率值互不相同的原因可以从流线分布状况来说明。若将孔隙内部流动通道等效为毛细管,则根据Poiseuille定律可知,在进出口端压差、通道长度与流体性质相同的情况下,通过该通道的流量与通道的尺寸相关。

(4)

式中,Q为流量;R为圆管半径;Δp为两端压差;η为液体粘滞系数;l为圆管长度。通过三维渗流流线图可以看出,各流动方向上流体都会汇集于一段孔隙通道中(见图5),即存在汇流通道,也可称之为流动控制喉道。在每段汇流通道中等距离取10个与流线相垂直的截面,并对该截面进行积分计算,可以得出X、Y、Z流动方向的汇流通道平均等效半径Rx、Ry、Rz分别为10.46、16.14、21.37 μm,等效半径比Rx∶Ry∶Rz=1∶1.39∶1.84,Rx4∶Ry4∶Rz4=1∶5.67∶17.4,而3个流动方向绝对渗透率之比Kx∶Ky∶Kz=1∶6.3∶16.3,与Poiseuille定律所表现的趋势基本吻合,可以认为不同流动方向上绝对渗透率产生差异的原因是汇流通道的尺寸大小不同。

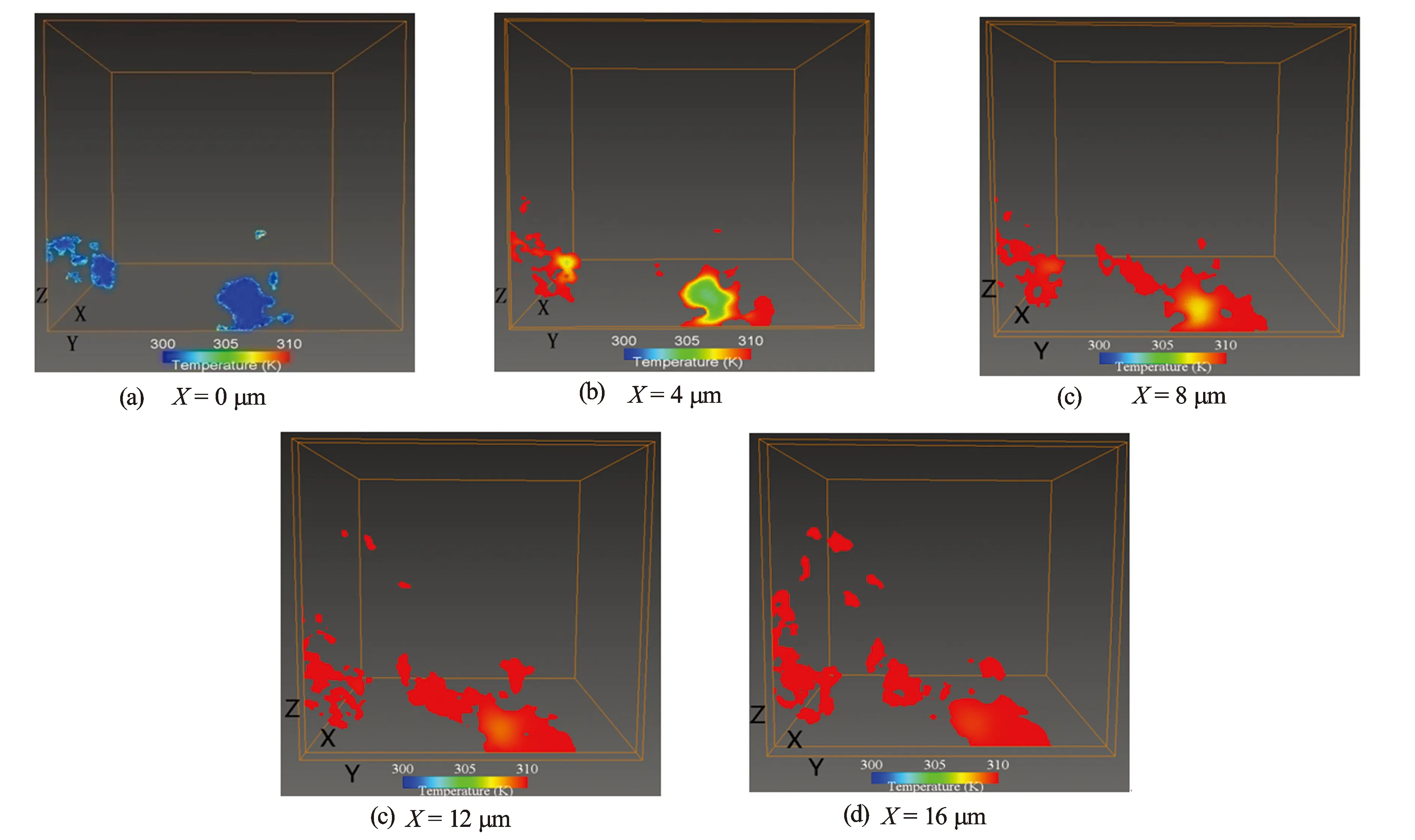
图6 X流动方向不同截面温度分布

3.3 温度场分析

通过流动方向上不同截面孔隙内温度云图可表示温度分布情况。以X流动方向为例,图6显示了距进口平面0、4、8、12、16 μm截面孔隙内流体温度分布状况,各个截面的最大温差为9.7、6.1、3.1、1.4、0.4 ℃,可以看出沿着该流动方向流体被迅速加热至壁面温度附近;同时通过设置将进口压力设置为100 Pa和500 Pa再计算后发现,上述各截面温度分布情况变化非常小,最大温差值基本不变。表明孔隙内部有着非常高的流动传热效率,主要是由于孔隙尺度小且流体流速低导致热混合充分。

4 结 论

(1) 使用Micro-CT技术对吉木萨尔致密油储层岩心样品进行扫描获取了岩心三维灰度图像,结合图像处理技术,解决了网格划分及优化的难题,成功将几何模型导入基于FVM的CFD软件ANSYS FLUENT中进行流动与传热耦合计算,与有限元软件COMSOL比,收敛速度大大加快,为研究孔隙中的流动与传热现象提供了一种新的途径。

(2) 通过对岩心内部渗流流场进行分析,发现在REV大小的重构区域内部流场存在一段特殊的汇流通道,岩心绝对渗透率大小与汇流通道的平均等效半径有关,其规律与Poiseuille定律所表现的趋势基本吻合。

(3) 通过计算在不同进口压力下温度场分布,获取了不同截面最大温度差;发现沿着流动方向上流体被迅速加温至壁面温度附近,说明孔隙级流动中有着很高的传热效率。

参考文献:

[1] 窦宏恩, 马世英. 巴肯致密油藏开发对我国开发超低渗透油藏的启示 [J]. 石油钻采工艺, 2012, 34(2): 120-124.

[2] OVAYSI S, PIRI M. Direct Pore-level Modeling of Incompressible Fluid Flow in Porous Media [J]. Journal of Computational Physics, 2010, 229(19): 7456-7476.

[3] BLUNT M J, BIJELJIC B, HU D, et al. Pore-scale Imaging and Modeling [J]. Advances in Water Resources, 2013, 51: 197-216.

[4] 黄丰. 多孔介质模型的三维重构研究 [D]. 合肥: 中国科学技术大学, 2007.

[5] 赵秀才. 数字岩心及孔隙网络模型重构方法研究 [D]. 北京: 中国石油大学, 2009.

[6] 刘学锋, 张伟伟, 孙建孟. 三维数字岩心建模方法综述 [J]. 地球物理学进展, 2013, 28(6): 3066-3072.

[7] DONG H, BLUNT M J. Pore-network Extraction from Micro-computerized-tomography Images [J]. Physical Review E, 2009, 80(2): 1957-1974.

[8] CHEN S, DOOLEN G D. Lattice Boltzmann Method for Fluid Flows [J]. Annual Review of Fluid Mechanics, 2003, 30(1): 329-364.

[9] OKABE H, BLUNT M J. Prediction of Permeability for Porous Media Reconstructed using Multiple-point Statistics [J]. Physical Review E, 2005, 70(6): 66-135.

[10] BOEK E S, Venturoli M. Lattice-Boltzmann Studies of Fluid Flow in Porous Media with Realistic Rock Geometries [J]. Computers & Mathematics with Applications, 2010, 59(7): 2305-2314.

[11] COON E T, PORTER M L, KANG Q. Taxila LBM: A Parallel, Modular Lattice Boltzmann Framework for Simulating Pore-scale Flow in Porous Media [J]. Computational Geosciences, 2013, 18(1): 1-11.

[12] 杜新龙. 低渗透砂岩油层微流动机理研究 [D]. 成都: 西南石油大学, 2012.

[13] 朱洪林. 低渗砂岩储层孔隙结构表征及应用研究 [D]. 成都: 西南石油大学, 2014.

[14] LIU Z, WU H. Pore-scale Study on Flow and Heat Transfer in 3D Reconstructed Porous Media Using Micro-tomography Images [J]. Applied Thermal Engineering, 2016, 100: 602-610.

[15] MOSTAGHIMI P, BLUNT M J, BIJELJIC B. Computations of Absolute Permeability on Micro-CT Images [J]. Mathematical Geosciences, 2013, 45(1): 103-125.

[16] ZHANG S, MAESTRA F D, COMBARET N, et al. The Analysis and Simulation of Rock Properties Using FIBSEM and Virtual Material Studio [M]. NAFEMS World Congress, 2011.

[17] 刘向君, 朱洪林, 梁利喜. 基于微CT技术的砂岩数字岩石物理实验 [J]. 地球物理学报, 2014, 57(4): 1133-1140.

[18] SIENA M, HYMAN J D, RIVA M, et al. Direct Numerical Simulation of Fully Saturated Flow in Natural Porous Media at the Pore Scale: a Comparison of Three Computational Systems [J]. Computational Geosciences, 2015, 19(2): 423-437.

[19] WU M, LI M, XU C, et al. The Impact of Concrete Structure on the Thermal Performance of the Dual-media Thermocline Thermal Storage Tank Using Concrete as the Solid Medium [J]. Applied Energy, 2014, 113(1): 1363-1371.

[20] YANG L, SHEN H. Effects of the Porous Media Distribution on the Performance Improvement for Isothermal Chamber [J]. Applied Thermal Engineering, 2015, 86(1): 301-308.

[21] 陶文铨. 数值传热学 [M]. 2版. 西安: 西安交通大学出版社, 2001.