联合神经网络在储层参数预测中的研究与应用

段友祥, 李根田

(中国石油大学(华东)计算机与通信工程学院, 山东 青岛 266580)

0 引 言

人工神经网络(Artificial Neural Network,ANN)能够从各个角度对生物神经系统的不同层次进行描述和模拟。代表模型有多层感知器、多层映射BP网络、RBF网络、Hopfiled网络、支持向量回归模型等等。地质储层参数预测领域常用有BP网络及优化的BP网络、RBF网络、支持向量回归模型等。

地质储层参数在建立地质模型中起着至关重要的作用。储层参数往往是通过井资料获得。在很多情况下,钻井取心仅限于某些层段,物性分析资料不足,不能全面客观地对储层进行评价。常规测井解释多通过经验公式或简化地质条件建立模型计算储层参数。对于解决复杂地质问题,二者都有很大的局限性和缺陷。很多学者提出了一些利用人工神经网络进行储层参数预测的方法。陈蓉等[1]在MATLAB平台上利用BP神经网络进行了储层的孔隙度和渗透率预测,并在实验中取得了良好的效果。李映涛等[2]利用BP神经网络进行了储层的孔隙度预测,并进行了实际应用。董兴朋[3]将遗传算法与BP算法相结合,利用改进的BP神经网络进行了储层的孔隙度和渗透率预测,该方法优化了神经网络结构,避免了BP算法陷入局部极小值得缺点,提高了预测精度。潘少伟等[4]利用改进的PSO-BP神经网络对储层参数动态预测,提高BP神经网络的收敛速度和泛化能力。Baneshi M等[5]采用优化的RBF网络通过井数据预测储层的孔隙度模型,并达到了预期的效果。Wu Xiongjun等[6]提出了基于可训练的径向基函数的RBF网络,并进行了储层的敏感性预测,其预测精度高于运用简单的径向基函数的RBF网络。而Na’imi S R等[7]采用地震数据运用支持向量回归的方法进行了储层孔隙度和含水饱和度的预测。同时,在其他领域,改进的BP网络[8]、RBF网络[9]和支持向量回归模型[10]被广泛应用。然而单一网络在地质储层参数预测问题上存在普适性不强、稳定性不高等缺点。

本文在深入研究的基础上,提出基于联合机制的新型人工神经网络模型(称为联合神经网络),是一种集多种人工神经网络组成的并行网络模型,实验表明,它在地质储层参数预测方面的表现明显优于其他的人工神经网络模型。

1 联合神经网络基本原理

1.1 基本思想

地质储层参数预测问题一般是通过已知的井资料和地质储层参数来获取经验公式或简单的地质模型,从而预测未知地区的地质储层参数[11]。人工神经网络方法进行地质储层参数预测一般包含2个阶段:①训练过程,利用已知的井资料和地质储层参数训练获取网络训练模型;②预测过程,利用得到的网络训练模型预测未知地区的地质储层参数。多年来,BP神经网络、RBF神经网络和支持向量回归这3种网络模型因其性能更高,技术比较成熟等优点,在地质储层参数预测方面都已有研究和应用,但也各有不足。

(1) BP神经网络是一种3层结构的前馈神经网络,它由输入层、输出层、一个或多个隐藏层组成,每个节点与邻层节点相连接,同一层的节点不相连。假设某神经元Y与N个神经元X相连,那么该神经元的状态输出为

(1)

式中,Wi表示神经元和神经元之间的连接权值;θ为连接偏置;f为神经元激活函数。

优势主要表现:①较好的泛化能力。当向网络输入训练时未曾见过的非样本数据时,网络也能完成由输入空间向输出空间的正确映射。②较强的容错能力。输入样本中带有较大的误差甚至个别错误对网络的输入输出规律影响很小。存在的缺陷:①网络训练容易陷入局部最优,失败的可能性较大。从数学角度看,BP算法为局部搜索的优化方法,但它要解决的问题为求解复杂非线性函数的全局极值,因此,算法很有可能陷入局部极值,使训练失败,利用训练失败的网络模型进行预测往往使得预测值误差较大。②网络结构的选择尚无一种统一而完整的理论指导,一般只能由经验选定,而网络的结构直接影响网络的逼近能力及推广性质。

(2) RBF神经网络[12]同BP神经网络一样,是由输入层、输出层和一个隐藏层组成的3层前馈网络,其中W表示连接权值,B为连接偏置。不同的是RBF神经网络以径向基函数(Radial Basis Function,RBF)作为隐藏层单元的基,即激活函数,构成隐藏层空间,隐藏层对输入矢量进行变换将低维的模式输入数据变换到高维空间。RBF神经网络的采用的径向基函数,通常定义为空间任一点到某一中心之间欧氏距离的单调函数。RBF基神经网络的激活函数是以输入向量和权值向量之间的距离作为自变量的,神经元Y的状态输出为

(2)

式中,Wi为该神经元与神经元之间的连接权值;B为连接偏置;radbas为神经元径向基激活函数。

RBF优势主要表现在:①逼近性能好。RBF神经网络有很强的非线性拟合能力,可映射任意复杂的非线性关系,科学界已经证明它可以任意精度逼近任意的非线性函数。②不存在局部极值。RBF神经网络是一种性能优良的前馈型神经网络,且具有全局逼近能力,从根本上解决了BP神经网络的局部最优问题。③学习过程收敛速度快。在RBF网络中,网络参数调节极为简单,因此学习过程收敛速度快。存在的缺陷:①RBF神经网络虽然可以任意精度逼近任意函数,但容错能力较弱。特别是在输入中带有较大误差甚至有个别错误时,网络的输出变化很大。②在训练样本较多的情况下,RBF网络的网络规模较大。

(3) 支持向量回归[13](Support Vector Regression,SVR)是通过寻找一个核函数,通过某种非线性映射将样本映射到一个高维空间(特征空间)。支持向量回归模型可以看成一个3层的网络架构,即输入层、中间层和输出层。该网络模型与普通的神经网络模型有所不同,但在分类预测的基本思想不变。对于给定的样本数据{(xi,yi)|i=1,2,…,k}(其中xi为输入值,yi为输出值),假设其服从函数y=f(x)。首先考虑用函g(x)=(ω·x)+b对样本数据集进行拟合,并使得函数f和g之间的距离最小,即损失函数最小。损失函数J见公式(3)

(3)

根据结构风险最小化原理,要使损失函数达到最小,则

(4)

s.t. {yi-f(xi)≤ε+δi,yi-f(xi)

利用Lagrange优化方法将问题转化为求函数最大值,再通过核函数K(xi,yi)将其转换到高维空间,从而得到回归函数f(x)见式(5)。目标方程对于样本是支持向量的。

(5)

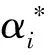
SVR优势:①将实际问题通过非线性变换转换到高维的特征空间,在高维空间中构造线性决策函数来实现原空间中的非线性决策函数,巧妙地解决了维数问题,并保证了有较好的推广能力,而且算法复杂度与样本维数无关。②理论上,得到的将是全局最优解,解决了在神经网络方法中无法避免的局部极值问题。③从本质上看,它避开了从归纳到演绎的传统过程,实现了高效的从训练样本到预测样本的“转导推理”,大大简化了通常的回归问题。④具有较好的泛化性和鲁棒性。它的不足:①对大规模训练样本难以实施。当向量维数m(样本个数)数目很大时,该矩阵的存储和计算将耗费大量的机器内存和运算时间。②在训练精度跟训练样本个数不成正比的情况下,直接训练不能充分利用样本数据,对样本数据造成浪费。

相关研究已经表明[14],当单个人工神经网络具有一定的准确性和差异性时,通过将它们组合,可以获得相比于单一神经网络更高的预测精度。基于此提出联合神经网络模型(Committee Neural Network,CNN),它是通过联合多种独立的人工神经网络组成的并行网络模型,其本质是通过结合多种网络的输出作为中间结果,再通过一定的组合和决策方式得到网络输出。因此,该网络主要包含了2个阶段。第1阶段通过BP神经网络、RBF神经网络和支持向量回归(SVR)等不同的基础神经网络单元分别预测获得各自的网络输出;第2阶段利用以上基础神经网络单元的输出作为输入,进入单层感知器(SLP)进行处理,从而得到联合神经网络模型的最终输出。

1.2 网络结构及工作原理

根据联合神经网络的基本思想,设计出CNN网络结构(见图1)。

图1 联合神经网络CNN结构

整个CNN网络中包含2部分。第1部分是由多个人工神经网络组成的基础神经网络单元,像BP网络、RBF网络或SVR等。基础神经网络单元不仅仅局限于这3种网络,可以是任何多种网络的组合。基础神经网络单元单独工作互不影响,且整个CNN网络的输入是针对每个基础神经网络单元,即每个基础网络单元有相同的输入,而经过不同的基础网络单元后会得到不同的输出。第2部分是将每个基础神经网络单元的输出通过一定的组合和决策方式得到一种网络输出。不同的组合和决策方式影响整个CNN网络的预测精度。对于简单的问题,基础神经网络单元预测精度较高且其输出差异不是很大,可以选择线性平均法或精度最高法。线性平均法是把基础神经网络单元输出的平均值作为最终输出。精度最高法是选择基础神经网络单元输出中精度最高的作为最终输出。对于基础神经网络单元输出差异较大的情况,则必须通过进一步的训练得到每个基础神经网络单元对最终输出的权重贡献值。对于权重的训练可以选择遗传算法或者单层感知器,单层感知器相比于遗传算法的优势是除训练得到的权重因子外还会得到一个微小的阈值,此阈值可以对最终的网络输出做一个微小的调整,可以大大提高了网络的预测精度。

单层感知器的结构简单,其状态输出见式(6)

(6)

作为CNN网络的一种组合方式,单层感知器必须是纯线性激活函数,即f为线性激活函数,其在CNN网络中所起的作用就是通过样本训练来得到基础神经网络单元对最终网络输出的贡献权值wi,加之阈值b,得到最终的网络输出y。

2 联合神经网络的仿真实现

实验选择了MATLAB平台进行仿真实现,以MATLAB中神经网络的工具箱为基础,通过调整神经网络的结构和规模,最终分别实现了BP网络、RBF网络、SVR模型以及CNN网络4种网络模型。

实验选择了与孔隙度相关的声波、密度、中子和自然伽马4种测井数据,经过主成分分析发现声波、密度、中子和自然伽马与孔隙度具有相关性,且4种测井数据之间不相关。因此,4种网络模型的输入参数为声波、密度、中子和自然伽马,输出参数为孔隙度。实验首先用带标签的数据进行训练,然后用训练得到的模型进行参数预测。

2.1 BP网络参数设置

BP网络中输入层到隐藏层的激活函数选择S型双曲正切函数,隐藏层到输出层的激活函数选择纯线性函数。具体结构见图2,S1是以双曲正切函数为激活函数的隐藏层,S2是以纯线性函数为激活函数的输出层。隐藏层的输出为a1=tansig(W1p+b1),输出层的输出为a2=purelin(W2a1+b2),其中a为状态值,W为各层的权值,b为网络偏置,上标代表网络的层数。

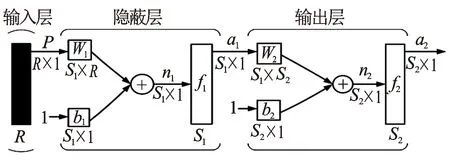
图2 BP神经网络预测单元

通过多次仿真实验与比较,确定了BP网络的参数。输入层设定4个节点;隐藏层节点的个数会影响训练的速度与预测的精度,隐藏层节点的个数大于6时,训练速度变慢,预测精度变化不大;隐藏层节点的个数小于6时,训练速度快,但预测精度较差。因此隐藏层节点设置为6,输出层节点为1。考虑到网络的收敛性和收敛速度与学习速率、最大训练次数、训练精度,权值初始化算法和学习算法有关,通过不同的实验并比较,发现权值初始化算法采用Nguyen-Widrow算法,反传学习算法采用Levenberg-Marquardt算法,设定学习速率0.1,最大训练次数1 000,训练要求精度0.001时能满足最终的性能要求。

2.2 RBF网络参数设置

RBF网络的径向基神经元的净输入采用距离函数(欧式距离)乘以偏置,并使用高斯径向基函数作为激活函数[15]。具体结构见图3。其中,S1代表由径向基神经元构成的隐藏层,S2是线性输出层。隐藏层的输出为a1=radbas(‖IW1,1-p‖·b1),输出层的输出为a2=purelin(LW2,1a1+b2),其中a为状态值,IW和LW为各层的连接权值,b为网络偏置,上标代表网络的层数。

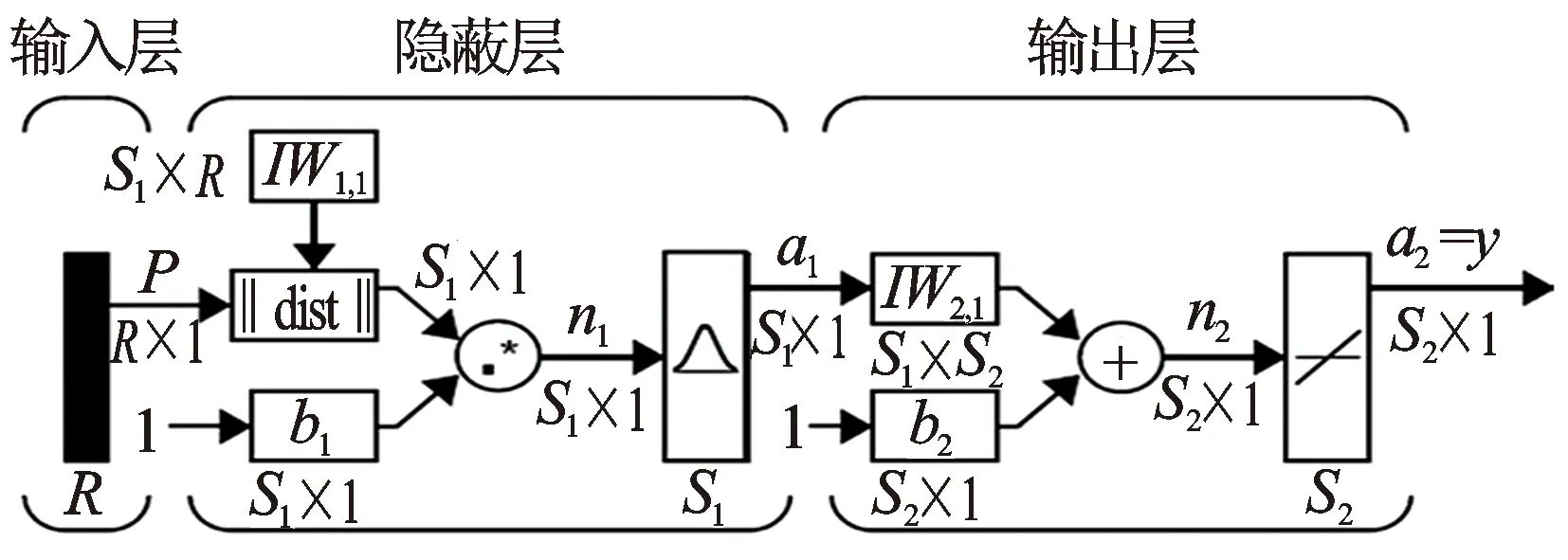
图3 RBF神经网络预测单元

该网络模型中,输入层设置4个节点,输出层设置1个节点,通过多次的网络训练并比较预测精度发现,当训练精度越高,网络的容错能力越低,反而最终的预测效果并不理想,所以在构建RBF网络时应该选择合适的训练精度,实验表明当训练要求精度为0.02时最终的预测精度较高,且此时隐藏层神经元数目为17个。实验过程中,由于实验数据经过归一化处理,样本数据统一在[-1,1]之间,因此,径向基函数选择了默认值。

2.3 SVR模型参数设置

图4 SVR预测单元

SVR模型中,输入为四维向量,训练样本的标签为一维向量。核函数选择高斯径向基函数[15],回归模型有3个重要的参数需要设置,分别是惩罚系数C,核函数参数γ以及拟合精度ε。通过多次实验并比较预测精度,设置惩罚系数为1 000,核函数参数为0.01,拟合精度为0.02。

2.4 联合神经网络

确定好3种神经网络参数,即3种基础神经网络单元建立完成,通过一个单层感知器组成一个并行的网络模型,即CNN网络。在该网络中输入依然为4个节点,分别经过BP网络单元、RBF网络单元和SVR模型单元之后得到3个中间输出孔隙度,它们再作为单层感知器的输入,最终得到CNN输出的孔隙度。

整个CNN网络模型关键在于基础神经网络单元的组合,训练后的基础神经网络单元对于最终的网络输出的权重贡献值和阈值通过单层感知器表现。实验中经过样本训练得到的权重值分别为0.791、0.167 4和-0.021 3,阈值为0.005 2。最后利用训练得到的CNN网络模型进行预测。

3 实验结果及分析

实验使用了某区块的3口油井的测井数据,3口井的标号分别为NB22-1-1、NB22-1-3和NB22-1-4。表1是对3口井的测井数据的描述。

实验采用BP网络,RBF网络,SVR模型和CNN网络4种人工神经网络模型,利用已知的井NB22-1-1数据分别建立孔隙度预测模型,再利用分别得到孔隙度预测模型,对井NB22-1-3和井NB22-1-4进行孔隙度预测,最后对这2口井的孔隙度预测值和已知实际值进行比较和分析。比较结果采用均方差(MSE)和相关系数(R)表示。比较和分析结果见图5、图6和表2。

通过比较4种神经网络,对于井NB22-1-3,联合神经网络的预测孔隙度与真实孔隙度的均方差最小,且相关系数最大;对于井NB22-1-4,同样联合神经网络的预测孔隙度与真实孔隙度的均方差最小,且相关系数最大。所以联合神经网络的预测效果要优于单一网络。并且通过多次实验发现,联合神经网络的预测效果会趋向于以上3种基础网络单元中预测效果最好的一种网络,且其均方差和相关系数也会达到最佳效果。因此,联合神经网络会自适应调节网络的结构,避免了某单一网络在参数预测时的缺点。

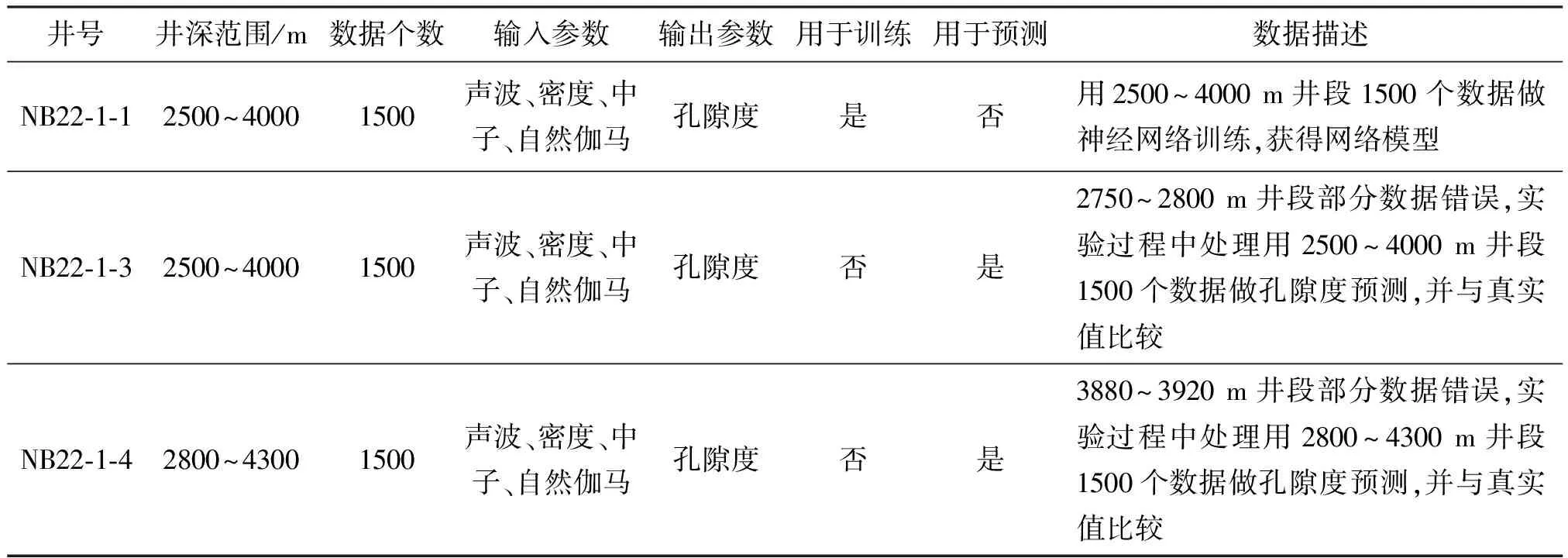
表1 3口油井的数据描述

图5 NB22-1-3井的孔隙度

表2 测孔隙度与真实孔隙度均方差(MSE)和相关系数(R)

从预测结果看,井NB22-1-3的预测效果要高于井NB22-1-4。这是由于网络的训练数据是从井深2500～4000 m井段得到的训练模型,网络模型对于在同一深度段的井NB22-1-3的预测效果较好,而对于井NB22-1-4的4000～4300 m井段的预测效果较差。

4 结 论

(1) 提出了以单一人工神经网模型作为基本单元,通过单层感知器联合BP神经网络、RBF神经网络和SVR模型组成的联合神经网络模型。

(2) 联合神经网络能自适应调节网络结构,较好地避免了单一网络在参数预测时的缺陷,提高了网络的鲁棒性。从预测效果上,该网络提高了预测的精度。

(3) 联合神经网络在地质储层参数预测方面的实际应用实验表明,其网络模型的适应性、预测的准确性都优于单一的人工神经网络模型。

(4) 联合神经网络的基础神经网络单元可以任意调节和改变。基础神经网络单元的预测性能越好,联合神经网络的预测性能也就越好。

参考文献:

[1] 陈蓉, 王峰. 基于MATLAB的BP神经网络在储层物性预测中的应用 [J]. 测井技术, 2009, 33(1): 75-78.

[2] 李映涛, 袁晓宇, 刘迪, 等. BP神经网络在测井解释中的应用研究 [J]. 西部探矿工程, 2013, 25(3): 45-48.

[3] 董兴朋. 相似度遗传神经网络在储层物性预测中的应用 [J]. 测井技术, 2012, 36(3): 267-271.

[4] 潘少伟, 梁鸿军, 李良, 等. 改进PSO-BP神经网络对储层参数的动态预测研究 [J]. 计算机工程与应用, 2014, 50(10): 52-56.

[5] BANESHI M, BEHZADIJO M, ROSTAMI M, et al. Using Well Logs to Predict a Multimin Porosity Model by Optimized Spread RBF Networks [J]. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2015, 37(22): 2443-2450.

[6] WU X J, JIANG G C, WANG X J, et al. Prediction of Reservoir Sensitivity Using RBF Neural Network with Trainable Radial Basis Function [J]. Neural Computing & Applications, 2013, 22(5): 947-953.

[7] NA’IMI S R, SHADIZADEH S R, RIAHI M A, et al. Estimation of Reservoir Porosity and Water Saturation Based on Seismic Attributes Using Support Vector Regression Approach [J]. Journal of Applied Geophysics, 2014, 107: 93-101.

[8] 于王乐, 汪家权. 改进的QGA-BP模型在复杂水质预测中的应用 [J]. 模式识别与人工智能, 2012, 25(4): 705-708.

[9] LIU X, DONG F, HE G, et al. Use of PCA-RBF Model for Prediction of Chlorophyll-a in Yuqiao Reservoir in the Haihe River Basin, China [J]. Water Science & Technology Water Supply, 2014, 14(1): 73-80.

[10] ZHANG J, YIN K, WANG J, et al. Displacement Prediction of Baishuihe Landslide Based on Time Series and PSO-SVR Model [J]. Chinese Journal of Rock Mechanics & Engineering, 2015.

[11] 徐基祥, 王才经. 综合地质、钻井和地震资料预测储层物性参数 [J]. 石油地球物理勘探, 1996, 31(1): 84-91.

[12] 刘永, 张立毅. BP和RBF神经网络的实现及其性能比较 [J]. 电子测量技术, 2007, 30(4): 77-80.

[13] 田英杰. 支持向量回归机及其应用研究 [D]. 北京: 中国农业大学, 2005.

[14] HANSEN L K, SALAMON P. Neural Network Ensembles [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12: 993-1001.

[15] 楼俊钢, 蒋云良, 申情, 等. 软件可靠性预测中不同核函数的预测能力评估 [J]. 计算机学报, 2013, 36(6): 1303-1311.