Excel在中职数学教学中的应用

刘慧敏

以职业为导向的中职数学课程改革的探索是当前中职数学教学研究的重要课题之一。本文主要介绍了Excel在中职数学教学中的实际应用，目的在于改进教师的教学模式和学生的学习方式，提高中职数学教学的有效性，提升学生的职业能力，进一步地突显了职业教育的特色。

一、引言

数学不仅仅是一种工具，它更是一個人必备的素养，它会影响一个人的言行、思维方式以及学习新知识的能力等等。对于中职生来说，他们一般不是以数学为终身职业，那么他们的数学素养不应该局限于能解多难的题，解题有多快，数学能考多少分，关键在于他们是否能够通过数学的学习获取一些做人做事的能力，提高其职业素养。因此，如何以职业岗位需求为导向，将数学教学的关注点转向学生职业能力的培养，实现数学课服务于专业学习、劳动就业，数学课满足培养学生职业发展能力的功能，成为中职数学教育工作者必须面对的重要课题。

Excel是Microsoft Office的组件之一，集文字、数据和图表于一体，除了普及性高、操作简便、入门容易等特点外，它还是大部分中职学生必需掌握的计算机基础。在中职数学教学中合理使用Excel，将《数学》课程与《计算机应用基础》课程结合起来，为中职数学课程改革提供了方向。本文主要讨论了Excel在中职数学教学中的实际应用，目的在于改进教师的教学模式和学生的学习方式，提高中职数学教学的有效性，提升学生的职业习能力，进一步地突显了职业教育的特色。

二、Excel在中职数学教学中的实际应用

1.利用Excel的计算功能，提高学生的数据处理能力

中等职业数学教学大纲将技能培养要求整合为“计算技能” “计算工具使用技能”“数据处理技能”，进一步体现了基础课为学生终身学习和生活服务的职责。中职数学中出现的运算，如乘方、开方运算，指数、对数运算、三角函数运算等，对于计算能力较弱的中职生来说很难掌握。如果数学课堂用来让学生处理这些繁杂的运算，不但会影响他们的学习兴趣，打击他们的学习热情，而且课堂也很容易变成无效课堂。然而，在课堂中合理利用 Excel的计算功能，它可以使得整个计算过程程式化、公式化，可操作性强，易于掌握，可以使得老师的讲授和学生的学习取得事半功倍的效果。下面以《基础模块》的内容为例，简单介绍Excel在中职数学运算求解和统计方面的应用。

例1：利用计算器求34.252×0.82-1÷18.25260.42-2的值（精确到0.001）。

分析：这个运算主要涉及乘、除、乘方以及开方运算。下面举例如何用Excel计算乘方和开方运算。要计算ab，需在单元格输入=（a）∧（b），如=18.252，则在单元格内输入（18.2）∧（5/2）。 要计算nam，可以先利用数学知识将根式化为分数指数幂nam=amn，再在单元格输入=（a）∧（m/n），如50.453，则在单元格内输入（0.45）∧（3/5）。

操作：打开Excel工作薄，在单元格A1内输入一个，再输入算式（见图1），这时在编辑栏和单元格中可同时看到输入的内容，按Enter键就会看到计算结果，此时结果是保留了小数点后六位，要精确到0.001，只需选定单元格，右击选定设置单元格格式——数值——小数位数，设置为3即可。

Excel在中职数学教学中的应用

例2：已知一个样本25，21，23，25，26，29，26，28，30，29，26，24，25，27，26，22，24，25，26，28。

（1）填写右面的频率分布表；

（2）画出频率分布直方图。

操作：

1.在Excel工作簿的单元格A2—B11中输入题目给定的20个数据。在A1输入“原始数据”，C1输入“接受数据”；接受数据为每个分组的右端点，即将22.5，24.5，26.5，28.5，30.5输到C2—C6中；

2.把题目给定的频率分布表输到A13—C18中，并在D13—D18中增加“频率/组距”一列；

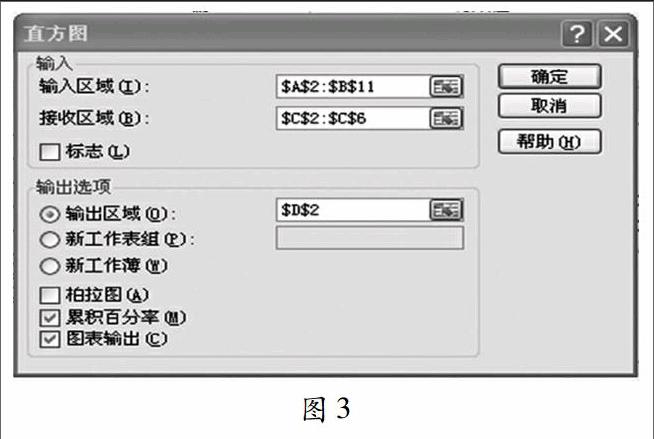
3.选择数据——数据分析，在数据分析对话框中选择分析工具“直方图”；出现对话框，如图 3填写；

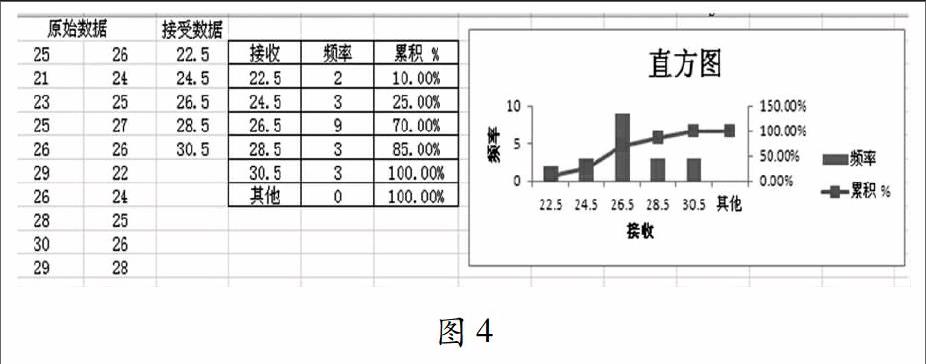
4.点击确定后如图 4，此时输出的直方图是频数直方图，输出表格中出现的频率是频数，将这些数据复制到B14—B18中。因此，借助Excel数据分析功能来确定每组频数，可以做到不重不漏。

5.在单元格C14内输入在“=B14/20”，选中C14的拖曳填充柄直到C18，计出频率；在D14内输入在“=C14/2”，选中D18的拖曳填充柄直到D18，计出频率/组距，得到频率分布表，效果如图5所示，即为例2的第一问。

6.选定分组和频率/组距两列（即单元格A13—A18和D13—D18）后，插入柱形图，选择堆积柱形图，可以得到频率直方图。这时可以选定频率直方图中的矩形，然后单击右键，选定“设置数据系列格式”，对直方图进行调整，直到得到满意的效果，见图6，即为例2的第二问。值得注意的是，“设置数据系列格式”命令里的系列选项对话框中的“分类间距”拖到0后，直方图中的每个矩形就不再有间隔。

2.利用Excel的函数功能，发展学生的数学应用意识

目前，中职生普遍认为数学课不能为专业课的学习服务，也与日常生活没有多大联系，这些都导致了学生感到数学知识无用。就算出现了一些与生活相关的实际问题，由于中职生的能力有限，也无法很好地解决，严重挫伤了学生学习数学的积极性。因此，在数学教学过程中，不但要求老师紧密联系生活实际，将生活中的问题引进课堂，而且还要求老师教会学生借助数学模型和计算机分析解决实际问题，让学生感受到用数学知识解决实际问题后的成功体验，让学生从生活中去学习数学知识，再把数学知识应用到生活中去。Excel有现成的300多个函数可用，还能根据用户的需要自定义函数，从而为运算求解各类数学模型以及数据处理分析提供了便利和拓展的空间。

例3： 某人向银行商业贷款100万用于购房，计划15年还清贷款，年利率为4.9%，请分别计算采用等额本息还款法和等额本金还款法每月还款额？

分析1：第一种办法是等额本息还款法，即把按揭贷款的本金总额与利息总额相加，然后平均分摊到还款期限的每个月中，每个月的还款额是固定的，但每月还款额中的本金比重逐月递增、利息比重逐月递减。

Excel中PMT函数是基于固定利率及等额分期付款方式，返回贷款的每期付款额。PMT函数的语法是：PMT（rate， nper， pv，[fv]，[type]）。PMT函数语法具有下列参数：第一，rate：贷款利率；第二：nper：该项贷款的付款总数； 第三，pv：现值，或一系列未来付款的当前值的累积和，也称为本金；第四，[fv]：可选参数，未来值或在最后一次付款后希望得到的现金余额，如果省略 fv，则假设其值为 0（零），也就是一笔贷款的未来值为 0；第五，Type：可选参数。数字 0（零）或 1，用以指示各期的付款时间是在期初还是期末。

PMT函数相关说明：PMT函数返回的支付款项包括本金和利息，但不包括税款、保留支付或某些与贷款有关的费用。特别要注意的是， rate 和 nper 单位的一致性。例如，同样是15年期年利率为 4.9% 的贷款，按年支付，rate 应为 4.9%，nper 应为15，但如果按月支付，rate 应为 4.9%/12，nper 应为15*12。

操作1：在单元格A1内输入=PMT（4.9%/12，15*12，1000000），得每月还款额为7，855.94。

分析2：第二种办法是等额本金还款法，是指贷款人将本金分摊到每个月内，同时付清上一交易日至本次还款日之间的利息。这种还款方式相对等额本息而言，总的利息支出较低，但是前期支付的本金和利息较多，还款负担逐月递减。

操作2：打开另一张工作表，在单元格C1内输入=1000000/180，计算每月偿还的本金，在单元格C2内输入=4.9%/12，计算每月的月利率。在A1输入1，A2输入=A1+1，选中A2的拖曳填充柄直到单元格出现180时为止，即第一列表示还款期，在B1内输入=C1+（1000000-（A1-1）*C1）*C2，得每月的还款额，见图7。

由计算结果看出，采用等额本金还款法，第一个月还款额为9638.89元，第二个月还款额为9616.20元，每月的还款额比上个月少22.69元，第80个月还款额为7846.76 ，因此，從第80个月开始每月的还款额要比等额本息还款法每月的还款额7，855.94少。

3.利用Excel的图表功能，创造自主探究的教学环境

Excel中的“图表”命令，可以完成由“表”到“图”的转换。这里的“图”指的是各种统计图，包括“平滑线散点图”。生成“平滑线散点图”的过程实际上也是“列表、描点、连线”的过程，这与中学函数作图的基本思想吻合。如果添置“滚动条”或者“数值调节按钮”控制参数，那么还能做出动态变化的函数图像。 著作就Excel环境下制作动态函数图像和几何图形的基本思想、操作方法作了较为详细的介绍，如：作出函数y=sin ωx的图像。动态演示是激发学生思考、促进学生理解的一种直观手段，同时也为学生自主探究学习创设了有利的条件。

三、结束语

本文给出的例子只体现了Excel表格的部分功能，它还可以产生大量随机数模拟实验，对数据进行统计分析，抽样，回归拟合，以及求解一些与实际有关的数学问题。Excel凭借它的易得性和好操作性，为教师的“教”和学生的“学”开拓了崭新的空间。Excel在中职数学教学中的应用，一方面给传统的数学教学注入了活力，克服了传统教学中的许多不足，有效地将“学数学” “做数学”和“用数学” 结合起来。另一方面能够做到基础课与专业课的学习前后连贯、步步深入，这种教学改革既能丰富教师的教学手段，提高教学效果，又能培养学生的实际技能，提高学生使用基本计算工具的能力，从而更好地满足社会对应用型人才的需求。

责任编辑 陈春阳