基于Fancher模型的钢板弹簧动刚度拟合精度研究＊

刘向陈伟赵景山严锋毛竹君

（1.东风商用车有限公司技术中心，武汉 430056；2.清华大学，北京 100081）

基于Fancher模型的钢板弹簧动刚度拟合精度研究＊

刘向1,2陈伟1赵景山2严锋1毛竹君1

（1.东风商用车有限公司技术中心，武汉 430056；2.清华大学，北京 100081）

基于Fancher模型采用最小二乘算法实现了钢板弹簧动刚度拟合，仿真与试验对比结果表明，Fancher模型具有较高的拟合精度，能够较好地模拟钢板弹簧的迟滞特性。进一步基于不同组数和行程的试验结果进行拟合精度研究，结果表明，基于2组试验数据即能够实现高精度拟合。结合2组动刚度试验结果和Fancher模型，通过参数辨识即可获取钢板弹簧动刚度特性，能够达到显著降低试验成本、缩短试验周期的目的。

1 前言

钢板弹簧非独立悬架在商用车中广泛采用，其刚度特性对整车平顺性和操纵稳定性有直接影响[1]，因此，在整车开发中，其刚度的合理设定非常重要。然而由于干摩擦导致的钢板弹簧载荷-变形曲线具有明显的迟滞特性，其动刚度具有显著的幅变特性[2]：在小变形时的乘适刚度（Ride Stiffness）是大变形时的名义刚度（Nominal Stiffness）的数倍[3]。钢板弹簧动刚度的幅变特性导致系统固有频率偏离原始设计值，不利于整车平顺性建模与分析。因此，建立高精度的钢板弹簧模型对整车设计具有非常重要的意义。

钢板弹簧的建模方法主要有基于板簧结构的三连杆模型[4]、Beam梁模型[5]和有限元模型[6]，以及基于板簧特性的Fancher模型[7～8]。在工程应用中，这些模型均需要结合试验进行对标或参数识别，因此动刚度试验是高精度建模过程中必不可少的内容。为提高模型对标精度，要求获取不同行程多组试验结果[4～9]，这势必导致试验周期长、成本高。如何通过建模的方法减少试验次数、降低试验成本、提高建模效率，在工程应用中具有巨大的价值和意义。文献研究表明，Fancher模型能够以较高的精度模拟钢板弹簧的非线性迟滞特性[8～9]。本文旨在通过研究Fancher模型的拟合精度，探究减少钢板弹簧动刚度试验的方法。

2 Fancher模型参数识别

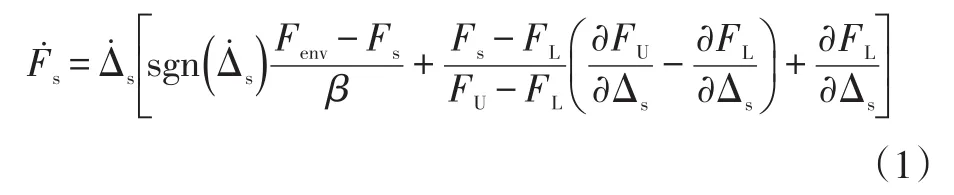
式中，Fs为垂直载荷；FU为加载边界；FL为卸载边界；Δs为变形量；β为加载/卸载延迟系数；

2.1 Fancher模型

加载与卸载边界获取方法：从垂向载荷为0时，缓慢加载至最大行程，然后卸载至0即可[3]。最大行程一般取2～3倍轴荷/板簧静刚度，且不大于限位块行程。目前常用的简化Fancher模型为[1]：

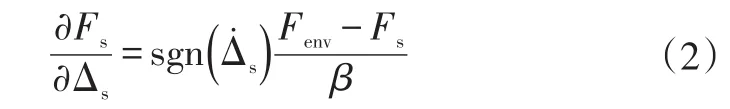
假设仿真步长较短，用一阶差分近似代替微分方程，进而可得到[8]：

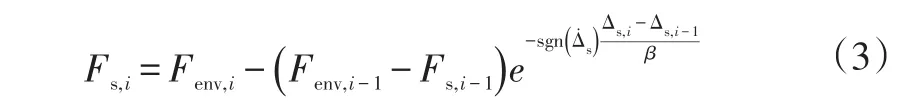
式中，i为载荷点编号。

延迟系数β用来描述和调整过渡边界的形状，考虑到加载和卸载的过渡边界形状不一定相同，因此有必要采用加载延迟系数βU和卸载延迟系数βL分别描述[3,8～9]。一般将过渡边界95%对应的悬架变形量定义为3β[9]。

教师要求学生从遗传物质的“信息流”角度理解蛋白质与核酸的关系，理解生命历程中基因选择性表达的具体过程：在特定时间DNA分子上特定的基因转录为mRNA，核糖体以mRNA为模板合成肽链，该过程中需要tRNA运载不同的氨基酸，mRNA密码子与tRNA的反密码子相互识别，决定肽链的氨基酸组成及排列顺序。蛋白质结构多样性的根本原因是基因的多样性。

加卸载边界FU和FL可以采用多项式进行数据拟合得到：

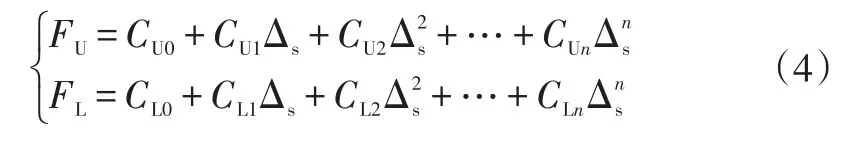
式中，系数CUi（i=0，1，…，n）和CLi（i=0，1，…，n）由试验数据拟合得到。

2.2 参数识别方法

采用上述Fancher模型进行描述的关键在于参数识别，该模型中需要识别参数为：延迟系数βU和βL；需拟合参数CUi和CLi。Fancher模型参数识别流程如图1所示，首先对原始数据进行截取和处理，然后通过多项式拟合得到加载和卸载边界参数CUi和CLi，并根据加载和卸载边界导数均值点获取延迟系数初值βU0和βL0，最后基于试验与拟合载荷误差最小，优化得到延迟系数βU和βL，其中优化目标函数为：

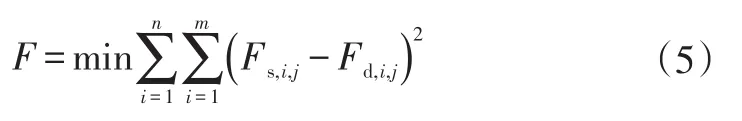
式中，n为不同钢板弹簧行程试验组数量；m为每组试验中数据采集点数量；Fd为试验载荷。

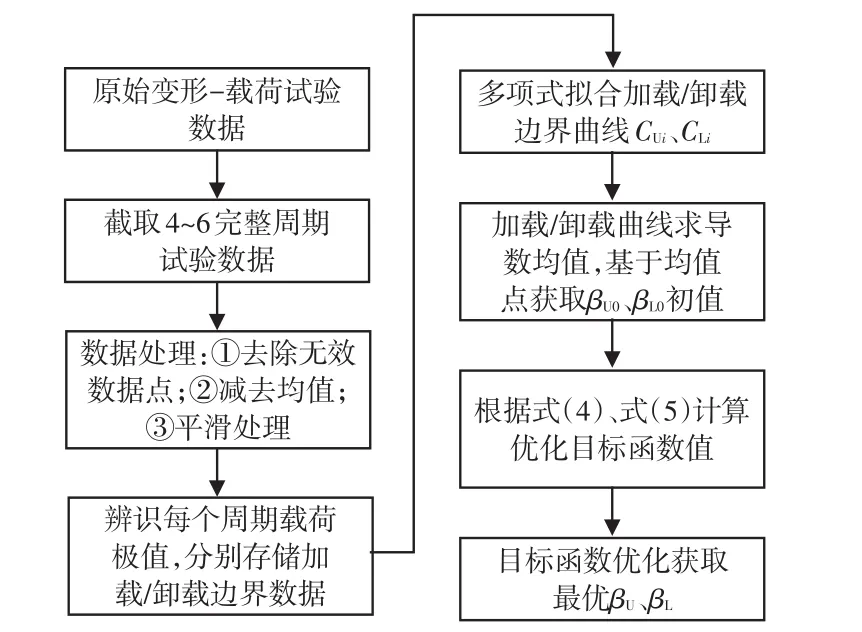
图1 Fancher模型参数识别流程

为了准确描述板簧非线性动刚度特性，需取多组行程的试验数据，如何通过尽可能少的试验数据获取模型的准确参数是降低试验成本、提高效率的关键。

3 钢板弹簧动刚度拟合

针对某商用车前悬架钢板弹簧进行了多组动刚度试验，试验行程分别为3 mm、5 mm、10 mm、15 mm和20 mm，试验细节不再赘述。

以10 mm行程为例，试验获取的时间-变形曲线、时间-载荷曲线及变形-载荷曲线分别如图2所示，由试验结果可知，试验加载频率对载荷无明显影响，因此可以采用Fancher模型进行模拟。不同行程试验钢板弹簧变形-载荷曲线如图3a所示，采用一次线性拟合得到的行程-刚度曲线如图3b所示。由试验结果可知，随着悬架行程增加、刚度减小，板簧刚度具有明显的幅变特性。

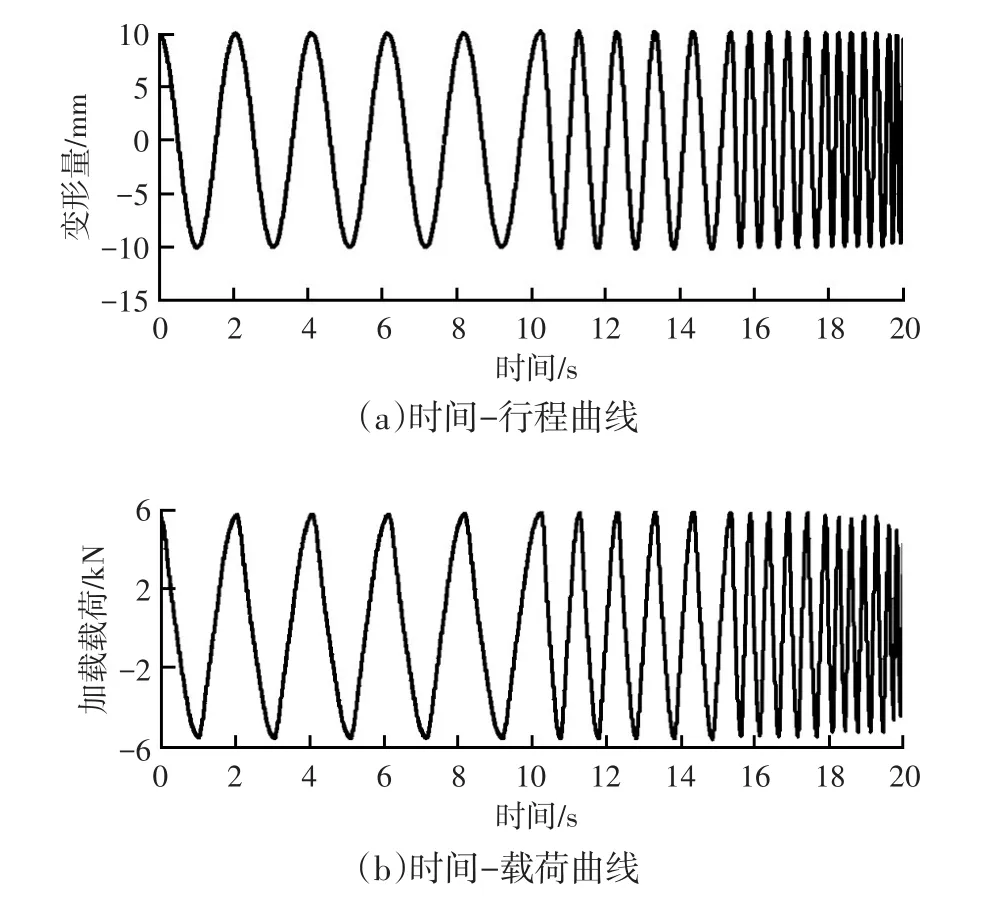
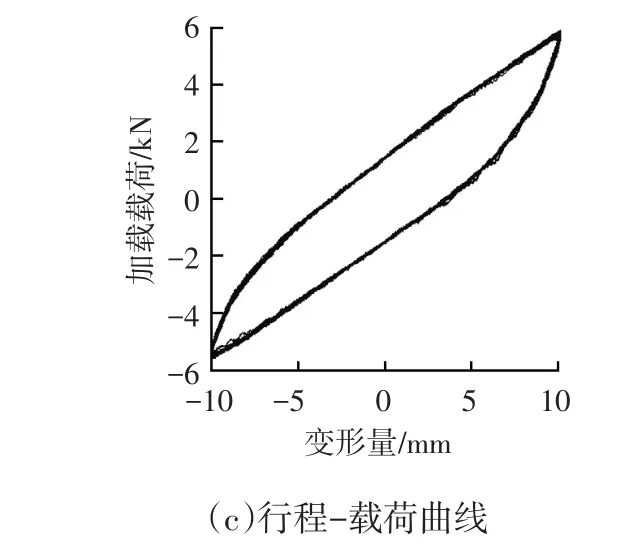
图2 10 mm行程试验结果

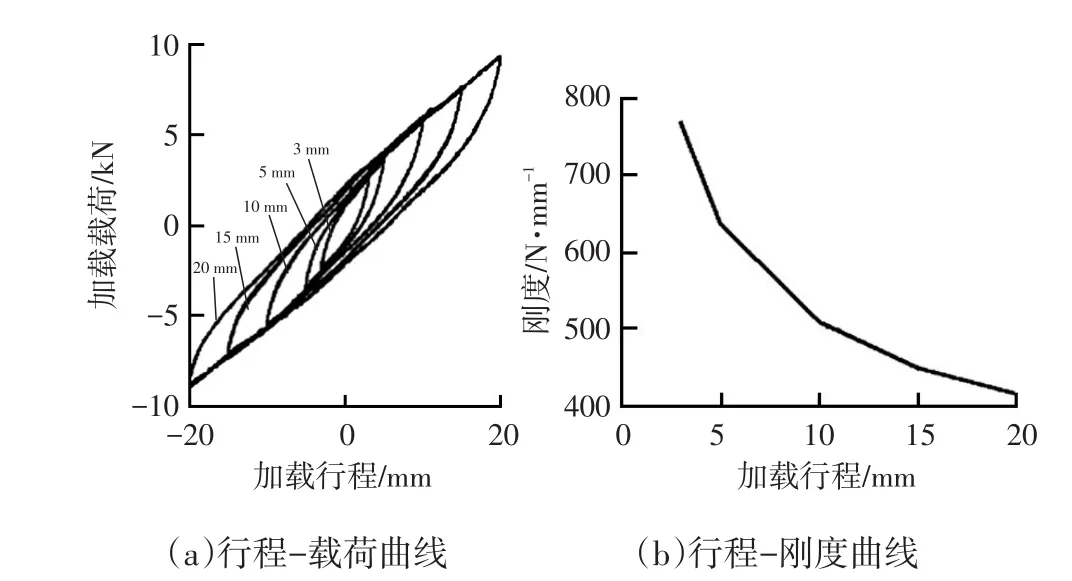
图3 钢板弹簧动刚度试验结果

3.2 动刚度拟合

根据图1所示的参数识别流程，可以得到钢板弹簧行程-载荷曲线拟合结果：βU=3.202 9、βL=3.101 4。基于Fancher模型的拟合结果与试验结果的对比如图4所示，由图4可知，拟合结果与试验结果具有较高的重合度。为了定量描述拟合精度，定义拟合平均误差为：

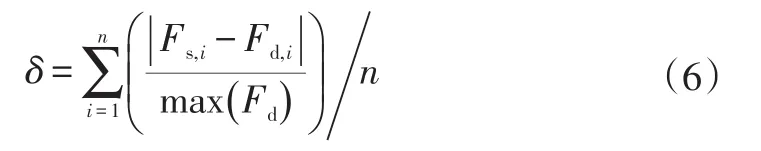
式中，Fs,i为第i点拟合载荷；Fd,i为第i点试验载荷。

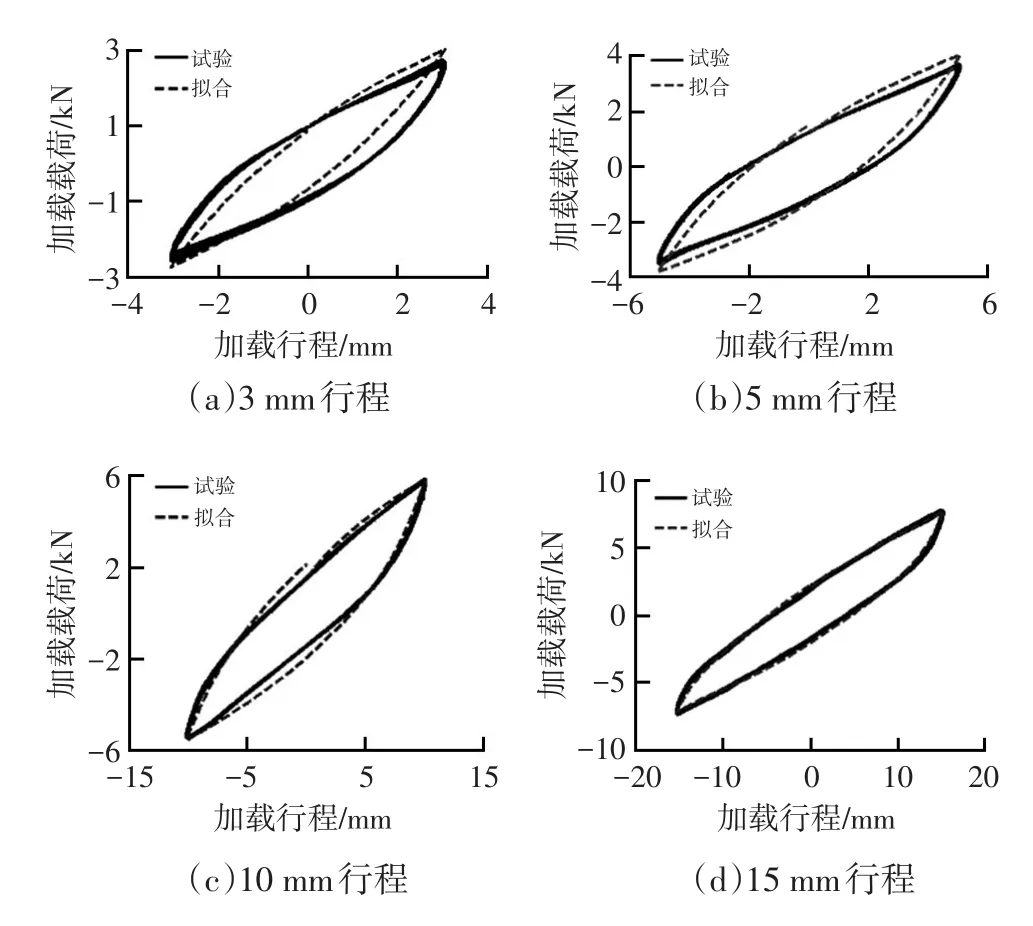
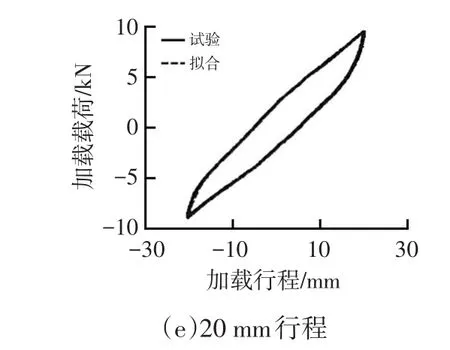
图4 基于Fancher模型的拟合结果与试验结果的对比

基于5组试验数据得到的拟合平均误差如表1所示，由结果可知，板簧行程越大，拟合精度越高，其中20 mm行程拟合平均误差仅1.01%，该误差主要源于加载和卸载边界采用多项式拟合的误差。

表1 Fancher模型拟合平均误差

4 拟合精度分析

由前述拟合结果可知，Fancher模型能够高精度地模拟板簧非线性迟滞特性，不过该模型需要结合多组板簧动刚度试验。为了达到降低试验成本、提高试验效率的目的，研究了基于少组试验的拟合精度。

考虑Fancher模型必须获取最大加载和卸载边界曲线，因此结合本文，必须采用行程最大为20 mm的试验数据；另一方面，为了尽可能提高效率，需要拟合试验参数组数尽可能少。分别研究了采用1组、2组和3组试验数据时的拟合精度，相应的拟合参数和参数识别结果如表2所示。

表2 不同组数和行程试验参数拟合结果

进一步，根据式（6）可以求得不同组试验拟合平均误差如表3所示，其中编号与表2中对应。由结果可知，仅采用1组（20 mm）试验结果时，能够实现20 mm行程高精度拟合，拟合平均误差仅为0.88%（误差主要为式（4）多项式拟合误差），而其他组行程拟合精度非常低，无法满足建模要求。相应的拟合行程-载荷曲线如图5所示，由图5可知，由于加载和卸载延迟系数为0，无法模拟载荷过渡段曲线。

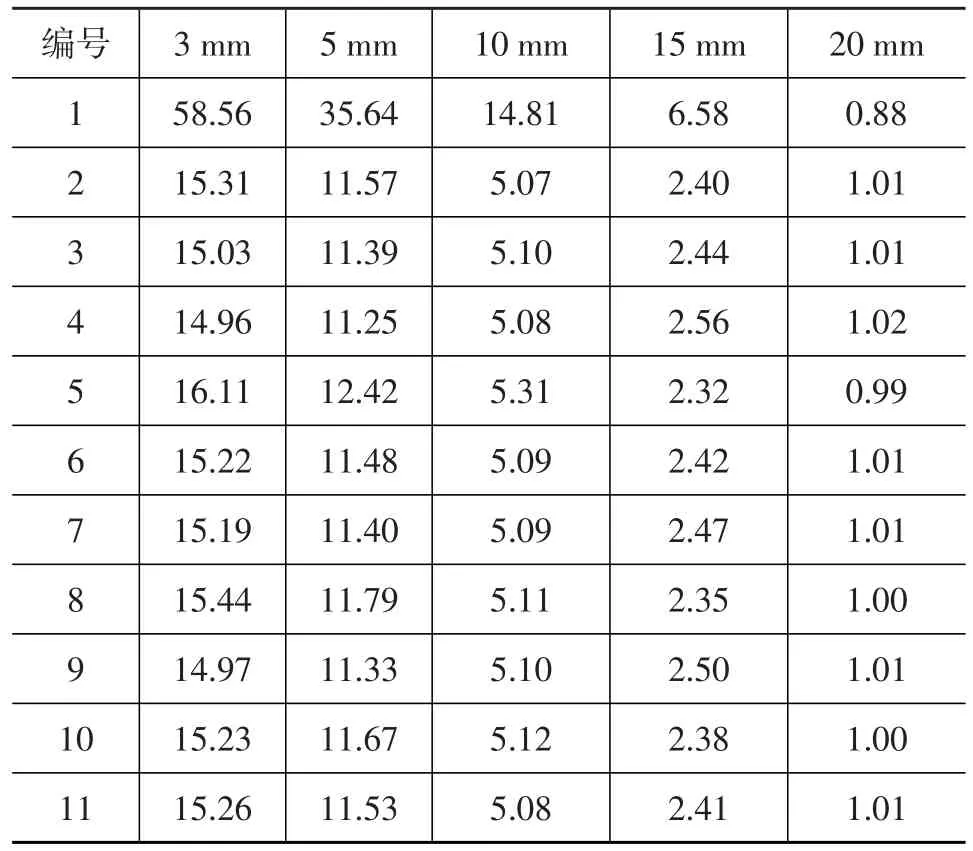
表3 不同组试验参数拟合平均误差 %

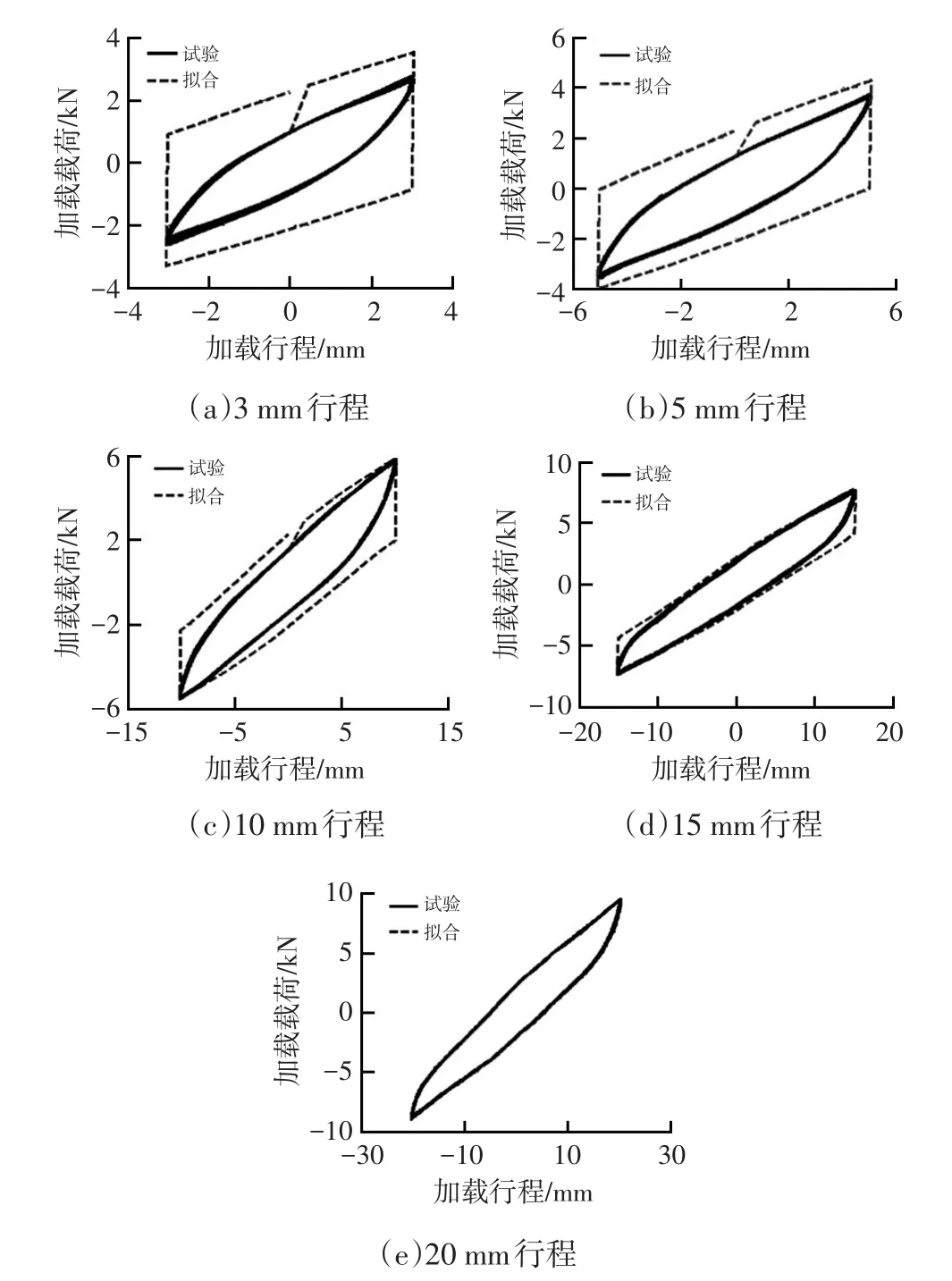
图5 拟合结果与试验结果的对比（1组数据）

当采用2组或3组试验结果进行拟合时，拟合平均误差与采用5组试验结果拟合非常接近，不同行程拟合误差最大差值为0.88%。分析结果表明，仅需2组试验结果即可达到较高的拟合精度。在实际应用中，可以将多组试验缩减为2组试验，达到大幅缩短试验周期的效果。

5 结论

本文首先提出了基于Fancher模型的板簧动刚度参数识别方法，并结合试验参数实现了某商用车前悬架板簧动刚度的高精度拟合。在此基础上，分析了不同组数和行程试验数据拟合得到的载荷曲线与试验载荷曲线的平均误差。研究结果表明，最少仅需要2组试验数据（其中一组必须为板簧最大行程试验）进行参数识别，即可实现基于Fancher模型的板簧动刚度高精度拟合。这一方法为板簧动刚度试验缩短周期和提高效率提供了理论支撑。

1 Salaani M K,Heydinger G J,Grygier P A.Heavy Tractor-Trailer Vehicle Dynamics Modeling for the National Advanced Driving Simulator.SAE 2003 World Congress& Exhibition，Detroit，2003.

2 卢荡.钢板弹簧干摩擦建模与仿真.计算机智能与工业应用国际会议，武汉，2010.

3 齐海政.高品质商用车动力学建模关键问题研究.长春：吉林大学，2011.

4 景立新，郭孔辉，卢荡.钢板弹簧三连杆模型参数辨识研究.汽车技术，2010（12）：10～13.

5 韩翔.基于ADAMS的钢板弹簧动力学建模方法及性能仿真.机械设计与制造，2009（10）：220～222.

6 叶南海，王利，闫彩伟，等.不同摩擦系数的少片变截面钢板弹簧性能分析.湖南大学学报：自然科学版，2015（8）：29～33.

7 Fancher P,Ervin R,MacAdam C,et al.Measurement and Representation of the Mechanical Properties of Truck Leaf Springs,SAE Technical Paper 800905，1980.

8 张绍龙.汽车悬架系统特性建模方法研究.长春：吉林大学，2011.

9 卢萍萍，逄淑一，齐海政，等.用于品质动力学仿真的悬架非线性承载模型.江苏大学学报：自然科学版，2011，32（5）：502～505.

（责任编辑 斛 畔）

修改稿收到日期为2016年10月10日。

Fitting Precision Analysis on the Dynamic Stiffness of Leaf Spring Based on the Fancher Model

Liu Xiang1,2,Chen Wei1,Zhao Jingshan2,Yan Feng1,Mao Zhujun1
（1.Dongfeng Commercial Vehicle Technical Center,Wuhan 430056;2.Tsinghua University,Beijing 100081）

The dynamic stiffness of leaf spring was fitted based on the Fancher model through least squares algorithm.The comparison between simulation and test has revealed that the Fancher model could simulate the hysteresis characteristics of leaf spring with high fitting precision.The fitting precision research was carried out based on different groups and mileage,and the results indicated that the dynamic stiffness of leaf spring could be simulated with high precision by considering only two groups of test data.As a result,the dynamic model of leaf spring could be established by combining two groups of test data and parameter identification of Fancher model,which will lead to obvious cost and time reduction of test.

Leaf spring,Fancher model,Dynamic stiffness,Hysteresis characteristics,Fitting precision

钢板弹簧 Fancher模型 动刚度 迟滞特性 拟合精度

U463.1

A

1000-3703（2017）03-0038-04

中国博士后科学基金项目（2016M602268）；湖北省重大科技创新计划（编号2014AAA003）。