间隙厚度对改进爆炸零门可靠性窗口的影响
2017-05-07杨小玉李燕华张郑伟王亚东温玉全谢佳良
杨小玉, 李燕华, 张郑伟, 王亚东, 温玉全, 谢佳良
(1. 北京理工大学爆炸科学与技术国家重点实验室, 北京 100081; 2. 国营第五二四厂, 吉林 吉林 132021; 3. 北方特种能源集团西安庆华公司, 陕西 西安 710025)
1 引 言
爆炸逻辑网络是由具有逻辑运算功能的爆炸元件构成,通过爆轰信号传递指令,实现可选择性输出,在引信和战斗部以及航空航天等诸多系统中有着广泛应用前景[1]。爆炸零门是构成爆炸逻辑网络的基础元件,其通过切断或破坏爆炸通道装药来阻断爆轰传递以实现网络逻辑功能,对爆炸逻辑网络的可靠性起决定性作用。爆炸零门按结构不同可分为三种类型: 拐角零门、接触零门和间隙零门[2]。拐角零门是由两个装药尺寸相同且相互垂直的沟槽通道组成,利用小尺寸装药爆轰波传播的拐角效应,实现爆轰波只能直线传播而不能绕过直角传播,沟槽尺寸是这种零门的关键设计参数。接触零门在控制通道与信号通道交叉处设置一段比正常尺寸小的通道,使控制通道的爆轰波在接触点附近变弱熄爆,利用熄爆后的冲击波将信号通道的装药破坏,进而切断信号通道爆轰波的传播通道,因此弱爆轰通道的尺寸是关键设计参数。间隙零门是在交叉处设置一段非爆炸性材料的间隙,利用控制通道爆轰波在间隙中产生的冲击波将信号通道的装药破坏,切断信号通道爆轰波的传播通道,一般将间隙厚度作为设计参数[3]。以上几种零门,其作用机理都是利用控制通道的爆轰波(冲击波)切断信息通道的沟槽装药,从而阻断爆轰波在信息通道的传播路径。只有提高零门设计参数的可靠性窗口,才能避免因机械加工工艺、装药工艺、炸药性能参数变化等因素对爆炸零门作用的影响,保证零门可靠作用。为此,国内外众多学者对此开展了研究,并取得了一定效果[4-6]。间隙零门因其结构简单、可靠性高等优点获得广泛研究,但其可靠性窗口较窄。2000年,温玉全[7]针对传统间隙零门作用可靠性差的问题,提出了一种改进的设计方法,即在间隙零门的通道交叉点前增加一个4 mm×2 mm的长方形泄爆槽,在一定程度上缩短了零门的关闭时间,提高了零门的作用可靠性。2006年,黄海龙[8]结合LS-DYNA的仿真结果,对该间隙零门做了进一步改进,在零门间隙处增加一个空气隙进一步缩短了零门关闭的时间,并通过试验验证了其性能更为优异。2016年,李燕华等[9]利用ANSYS/LS-DYNA数值模拟分析表明,增设圆形空气隙弱化了间隙强度从而有助于冲击波的衰减和零门间隙的打开,并得到了装药尺寸为0.8 mm×0.8 mm爆炸零门的间隙厚度窗口,但未考虑其可靠性的时间窗口问题。
在实际工程应用中,爆炸零门可靠作用存在一个时间窗口,在这个时间窗口内零门才能够正常作用,它是衡量爆炸逻辑零门可靠性的一个重要指标。以往的研究多通过试验的方式,但由于含圆形空气间隙间隙零门可靠性的影响因素众多,需进行大量的试验。近年来,随着计算机技术和数值算法的发展,数值模拟技术能够解决爆炸冲击中高应变大变形等问题,为爆炸零门的研究提供了一个可行的研究途径。
为了探究间隙厚度对零门可靠性时间窗口的影响,本研究借助LS-DYNA软件,对含圆形空气隙改进间隙零门进行三维数值模拟,计算了不同间隙厚度下间隙零门的可靠作用的时间窗口,并进行了试验验证。
2 爆炸零门作用原理及关键因素解析
含圆形空气隙改进间隙零门(以下简称“零门”)是一个五特征参数零门,特征参量为沟槽尺寸d、间隙厚度L、方槽与装药沟槽间距l、方槽尺寸m×n×d、圆孔空气隙尺寸Ф,其结构如图1所示。5个特征参量共同决定着零门的切口宽度和关闭时间,其中切口宽度主要影响零门关闭的可靠性,而关闭时间则制约着爆炸网络的作用时序与小型化。

图1含圆形空气隙改进间隙零门的结构示意图
Fig.1The schematic diagram of improved gap null gate configuration with round air groove
为了研究该爆炸零门可靠作用的时间窗口,设计一种自锁的网络试验件,如图2所示。该试验件包含输入端I、输出端O和零门N以及传爆通道,爆轰信号从输入端导入后,起爆沟槽装药产生自持的爆轰波,并在三通结构T进行分束,一路继续沿直线传播,率先抵达爆炸零门N并通过破坏附近沟槽装药实现零门关闭,该线路为控制通道C。另一路沿T的侧向进行传播,该线路命名为信息通道S。
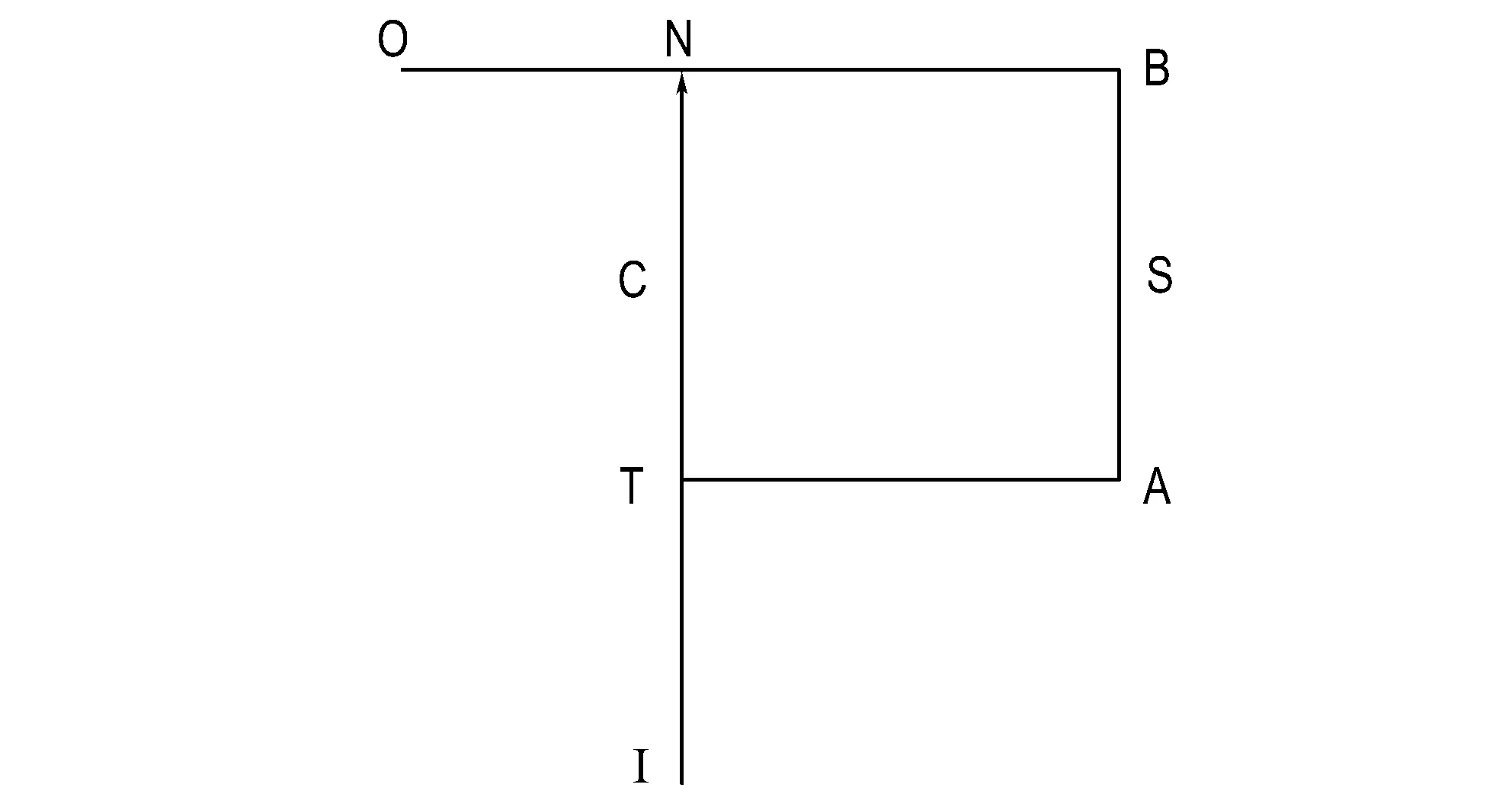
图2改进零门关闭时间的研究装置示意图
Fig.2The schematic diagram of device to study the improved null gate closing time
其最终能否通过N实现对外输出,则取决于S与C的长度差及C路爆轰波关闭零门的速度。其估算公式为:
信息通道的传爆时间:t1=LTABN/D
控制通道的传爆时间:t2=LTCN/D
线路时差: Δt=t1-t2
零门关闭的时间:tc
零门成功关闭的判据: Δt>tc
式中,D为固定装药尺寸和装药工艺条件下的爆速。Δt可通过爆炸网络设计得到控制,而tc由于受5个特征参量的共同影响,目前无法进行精确计算,只能采用实测值。由于结构尺寸以及装药的工艺偏差,实际爆炸零门关闭时间不是一个确定值,其可靠性时间窗口可用图3表示。图3中,p-t曲线为零门关闭的概率曲线;t1为不能关闭零门的最大时间间隔;t2为高概率能关闭零门的最小时间间隔;R为关闭零门的概率。当Δt
为了预估t2,为设计微小型快速响应爆炸零门提供技术支撑,采用单一因素分析法进行初步探讨,即通过重要度筛选确定间隙厚度为重点研究对象,并将其他特征参量进行固化,通过仿真和试验相结合的手段获得间隙厚度对零门关闭时间的影响规律。
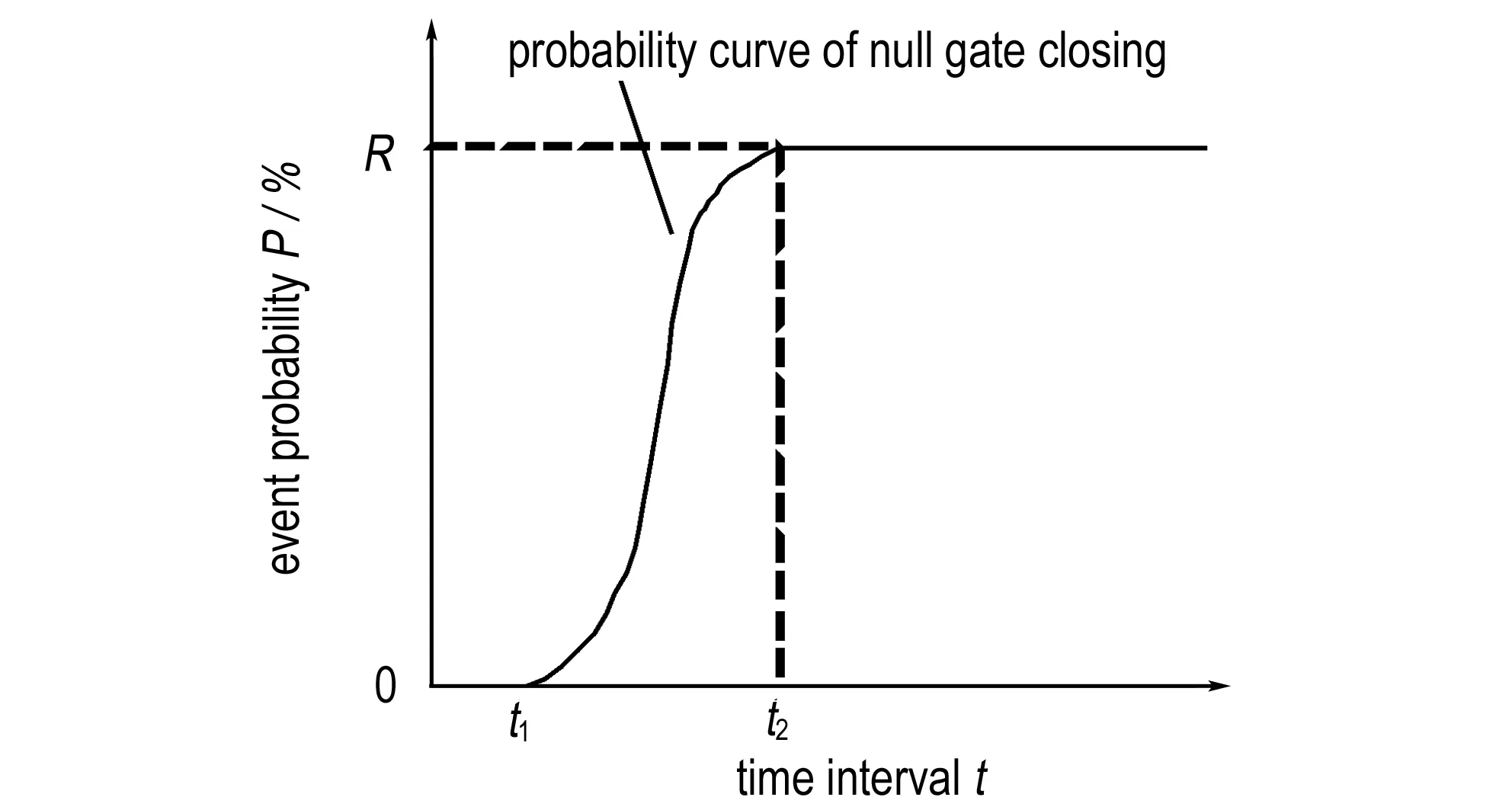
图3含圆形空气隙改进间隙零门关闭时间间隔的可靠性窗口曲线
Fig.3Reliability window curve of closing time interval of improved gap null gate with round air groove
3 数值仿真研究
3.1 仿真模型建立
利用LS-DYNA软件针对不同间隙厚度L零门的可靠性窗口进行分析,其变量范围是0.6~1.1 mm; 沟槽尺寸为0.6 mm×0.6 mm; 方槽与装药沟槽间距为0.1 mm,泄爆方槽的尺寸为4 mm×2 mm×0.6 mm; 圆形空气隙尺寸为Ф0.6 mm×0.6 mm。采用上节的方法研究零门的关闭时间,同时为了缩减有限元模型,将两通道的爆轰波由共输入改为单独输入,并将通道的长度差直接换算成起爆时差,如图4所示。
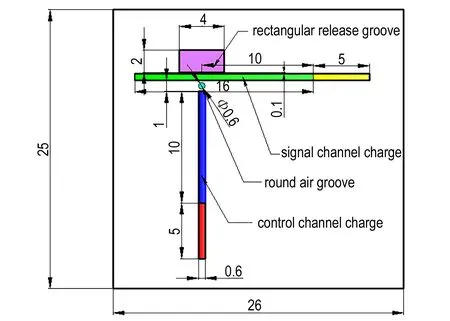
图4改进间隙零门基板模型(unit: mm)
Fig.4The physical model of improved gap null gate(unit: mm)
具体建模过程: 将控制通道和信息通道均分为两段,第一段(长度均为5 mm)采用高能炸药燃烧材料模型和JWL状态方程,用来代替起爆装药; 第二段(信息通道长度为16 mm,控制通道长度为10 mm)均采用点火增长模型模拟装药非理想爆轰,且信息通道第二段被起爆端面到间隙中心的距离为10 mm,具体尺寸分布如图4所示。此结构中信息通道和控制通道的有效路径差为零,因此,需要人为设置不同的起爆时序来获得不同的时间间隔Δt。通过仿真不同起爆时间间隔下零门作用的成功性,达到研究零门可靠性时间窗口的目的。
在数值模拟过程中,采用Lagrange算法,并利用关键字*INITIAL_DETONATION设置起爆参数,起爆点分别设置在控制通道和信息通道装药端面,有限元模型如图5所示。

图5改进间隙零门有限元模型
Fig.5The finite element model of improved gap null gate
3.2 材料模型及参数
3.2.1 炸药材料模型及参数
控制通道装药和信息通道装药前段等效起爆装药采用高能炸药燃烧材料模型和JWL状态方程[10],后段装药采用点火增长模型来描述小尺寸装药的非理想爆轰状态。点火增长模型除利用JWL状态方程来描述未反应炸药和反应产物的状态外,还引入了一个描述炸药受冲击反应的反应速率方程:
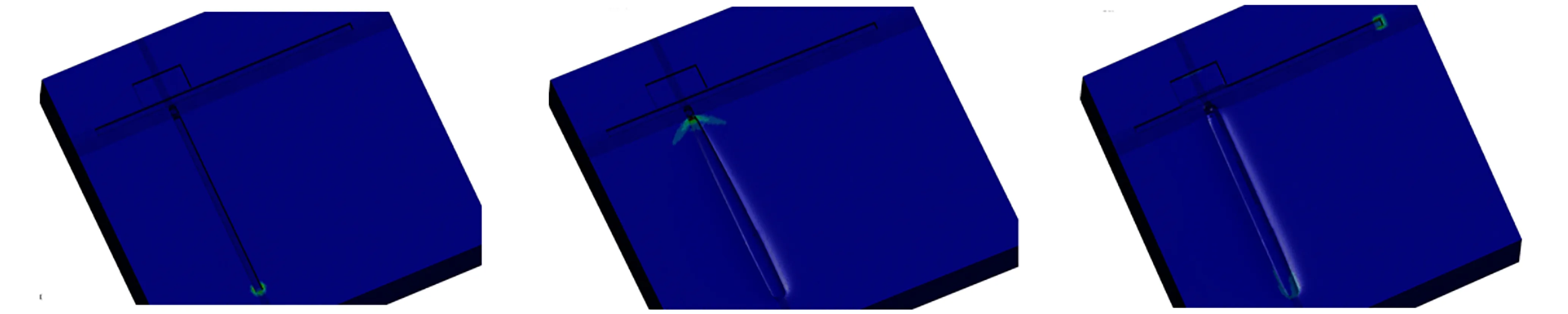
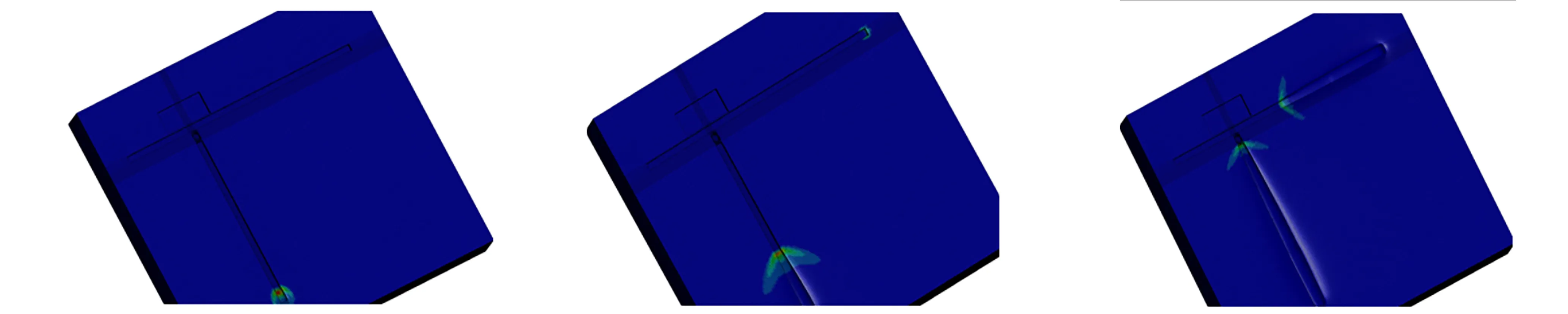
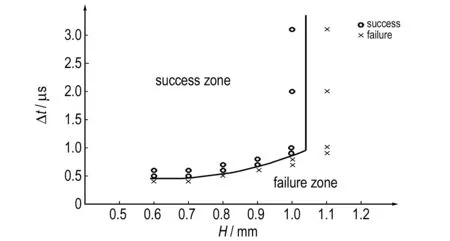
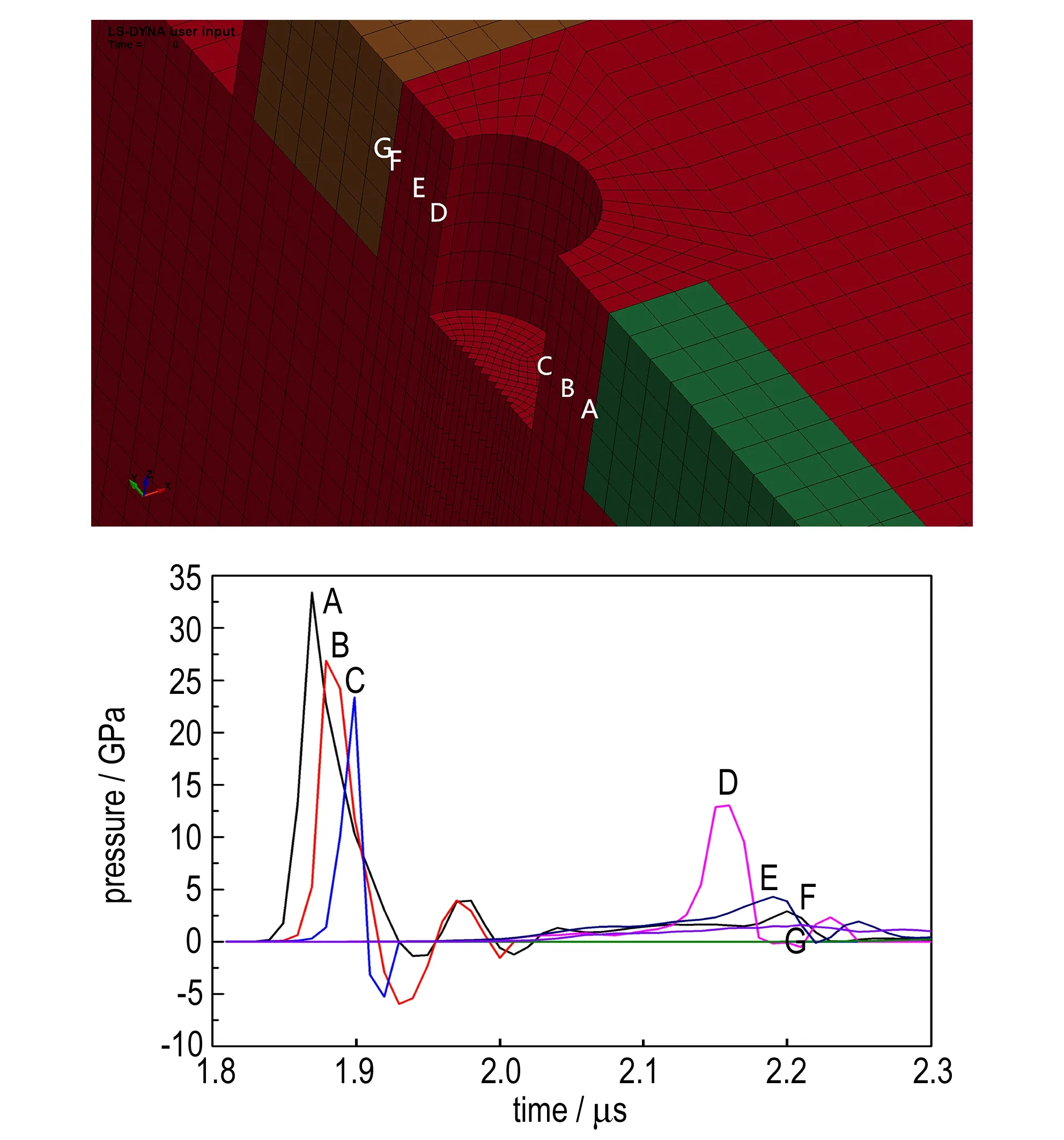
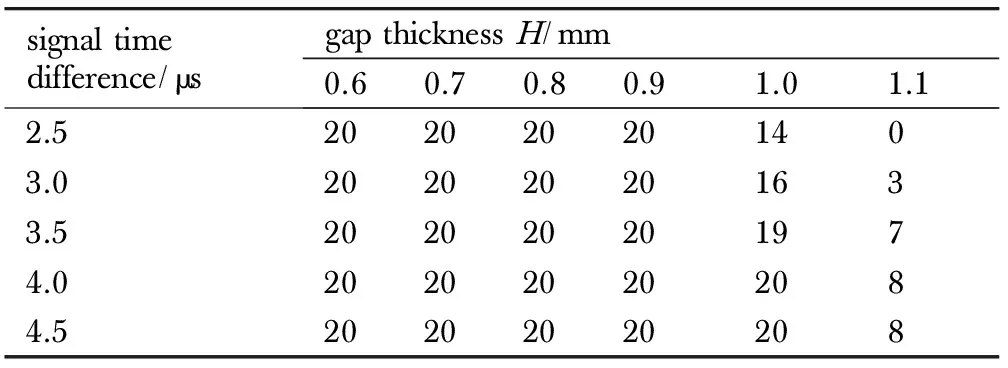
0 (1) 式中,F是炸药的反应度(F=0表示没有反应,F=1表示反应完成),t为反应时间,μs;p为压力,GPa;ρ为装药任意时刻密度,ρ0为装药初始密度,g·cm-3;I、x、b为控制点火起爆程度的参量,I单位为μs-1,b和x无量纲; 参数a是阻止点火的临界压缩度,无量纲,仅当压缩度ρ/ρ0>1+a时,装药才被点火;G1、c、d和y控制点火后反应的早期增长,G1单位为Mbars-z·μs-1,c、d和y无量纲;G2、e、g和z确定高压反应速率,G2单位为Mbars-zμs-1,e、g和z无量纲;Figmax、FG1max和FG2min用以控制反应速率三项的打开和关闭,当反应度F>Figmax时,关闭点火项; 当反应度F>FG1max时,关闭点火增长项; 当反应度F>FG2min时,打开高压反应速率项;F、Figmax、FG1max和FG2min均为无量纲量。 由于所用网络装药为以HMX为基的某型标准传爆药,其组分与LX-10接近,故参数选取参考文献[11],具体参数见表1。 表1网络装药的点火增长模型参数[11](装药密度ρ=1.77 g·cm-3) Table1Ignition and growth model parameter of network charge (ρ=1.77 g·cm-3) unreactedJWLEOSproductJWLEOSreactionrateparametersA=952200GPaA=722.4GPaI=7.43×1011μs-1B=-5.944GPaB=9.02GPaa=0.0R1=14.1R1=4.6b=0.222R2=1.41R2=1.3x=4.0w=0.8867w=0.38Figmax=0.3Cv=2.7813×10-3GPa/KCv=1×10-3GPa/KG1=0.0Mbars-zμs-1T0=298KE0=10.2GPac=0.0shearmodulus=5.0GPad=0.0yieldstrength=0.2GPay=0.0FG1max=0.3G2=2432.0Mbars-zμs-1e=0.222z=2.0g=0.667FG2min=0.0 3.2.2 约束材料的本构模型及参数 爆炸零门的约束材料为LY-12铝合金,为描述其在爆轰动态加载下高应变率塑性变形行为,选用Johnson-Cook模型[12]。Johnson-Cook模型是一个经验性的粘塑性本构模型,其能较好地描述材料的加工硬化效应、应变率效应和温度软化效应[12]。Johnson-Cook模型将屈服应力表示为: (2) 此外,为了描述LY-12铝合金的破坏失效行为,引入Johnson-Cook失效准则[12],其失效应变定义为: εf=D1+D2exp(D3σ*)(1+D4lnε*)(1+D5T*) (3) (4) 式中,Δε为加载过程中的等效塑性应变增量,s-1;σ*为平均应力与等效应力的比值,无量纲;D1、D2、D3、D4、D5为常数,无量纲。当D达到1.0时,材料失效。LY-12铝合金的相关模型参数[12]如表2所示。 表2LY-12铝合金的相关模型参数 Table2The correlation model parameters of LY-12 aluminum alloy ρ/g·cm-3A/MPaB/MPaCnmD1D2D3D4D52.83696840.00830.731.70.130.13-1.50.0110 3.3.1 零门关闭时间 间隙厚度1.0 mm,起爆的时间差Δt=3 μs时,零门的作用过程如图6所示。t=0 μs时,控制通道装药被起爆(图6a);t=2.2 μs左右时,信息通道爆轰波达到零门,开始切割零门(图6b);t=3.0 μs时,信息通道装药被起爆(图6c);t=4.1 μs左右时,信息通道爆轰波传播,此时零门已被破坏(图6d);t=6.0 μs,从信息通道传过来的爆轰波已经熄爆(图6e); 说明间隙零门可实现功能。 间隙厚度1.0 mm,起爆时间差Δt=0.7 μs时,零门的作用过程如图7所示。t=0 μs时,控制通道装药被起爆(图7a);t=0.7 μs左右时,信息通道装药被起爆(图7b);t=2.2 μs时,信息通道爆轰波达到零门,开始切割零门(图7c);t=2.6 μs左右时,信息通道爆轰波达到零门(图7d);t=3.9μs左右时,信息通道装药的爆轰波已通过零门达到装药末端(图7e); 说明间隙零门未实现功能。 采用相同的数值模拟方法,计算了不同间隙厚度下零门实现功能的时间差Δt,结果如图8所示。 从图8可看出,在实线左上区域为成功区域,零门功能均能实现,而右下区域为失效区域,零门功能均不能实现,实线所在位置即为零门实现功能的分界线,即: 当间隙厚度确定时,其纵坐标值为零门实现功能的最小时间差Δt; 当零门实现功能的最小时间差Δt确定时,其横坐标值为零门实现功能的最大间隙厚度。 a.t=0.0 μsb.t=2.2 μsc.t=3.0 μs d.t=4.1 μse.t=6.0 μs 图6含圆形空气隙改进间隙零门实现功能的作用过程 Fig.6The action process of improved gap null gate with round air groove to achieve the function a.t=0.0 μsb.t=0.7 μsc.t=2.2 μs d.t=2.6 μse.t=3.9 μs 图7含圆形空气隙改进间隙零门未实现功能的作用过程 Fig.7The action process of improved gap null gate with round air groove not to achieve the function 图8含圆形空气隙改进零门的数值模拟结果 Fig.8Numerical simulation results of improved null gate with round air groove 此外,特别注意到,零门实现功能的最小时间差Δt(零门关闭时间)并不是随着间隙厚度的增加线性增加,而是在间隙厚度1.1 mm时有一个大的跳跃,分析原因: 本设计的改进零门的临界间隙厚度在此间隙厚度附近,即当零门间隙厚度L≥1.1 mm,无论起爆时间差多大,零门功能均不能实现。 3.3.2 零门间隙破坏程度及冲击波压力 对于爆炸逻辑零门而言,在固化装药工艺的前提下,间隙的厚度直接影响零门的破坏程度,从而决定着零门能否实现其关闭功能。不同间隙厚度下的零门破坏程度可通过三维数值模拟来呈现,如图9所示,仿真中提取5 μs时的破坏情况,此时爆轰冲击过程已结束,零门不再继续被破坏。 a.H=1.0 mmb.H=0.9 mmc.H=0.8 mm d.H=0.7 mme.H=0.6 mm 图9含圆形空气隙改进间隙零门破坏程度 Fig.9Damage degree of improved gap null gate with round air groove 从图9可看出,间隙厚度越小,零门破坏程度越大。其因有二: 一方面,间隙厚度越小,零门的结构强度越弱,易被破坏; 另一方面,间隙厚度减小,降低了对冲击波的衰减作用,致使通过零门达到信息通道的冲击压力偏大,破坏作用增强。但从零门结构的破坏程度来看,间隙厚度越小,越有利于零门关闭,然而,衰减后的残余冲击波是否会导致信息通道被殉爆,也是决定零门是否成功关闭的因素之一。 为此,以间隙厚度H=1.0 mm为例,分析间隙对控制通道冲击波的衰减效应,提取爆轰波传播路径上中心单元的压力历程曲线,如图10所示。从图10可看出,控制通道装药形成稳定爆轰波传播到零门间隙,首先受到金属铝阻挡开始衰减,单元A、B、C的压力峰值依次降低,再经过空气隙大幅衰减到达单元D,再次经过金属铝的衰减,单元D、E、F的压力峰值依次降低,最终达到信息通道装药单元G的冲击波压力为1.26 GPa,远小于沟槽装药的冲击波起爆阈值6.45 GPa[9]。 通过一系列仿真,提取不同间隙厚度下,到达信息通道装药的G单元冲击波的峰值,见表3。 从表3可看出,间隙厚度越小,通过间隙到达信息通道装药的冲击波强度越大,但均低于网络用药的起爆阈值6.45GPa。由表中数据还可以预见,当间隙厚度继续减小时,冲击波强度势必超过起爆阈值并产生殉爆,因此,间隙厚度并非越小越可靠,合理控制间隙厚度是决定零门能够成功关闭的必由之路。 图10含圆形空气隙改进间隙零门爆轰波传播路径上单元的压力曲线 Fig.10Pressure curves of several elements in detonation wave propagation path of improved null gate with round air groove 表3到达信息通道装药时的冲击波强度 Table3Shock wave intensity at the arrival of signal channel charge H/mm1.00.90.80.70.6pmax/GPa1.262.443.264.615.89 Note:His the gap thickness;pmaxis the peak of shock wave pressure arrived at signal charge. 为了验证仿真结果,设计了如图11所示的五组网络试验件,每组试验件20个,间隙厚度分别为0.6,0.7,0.8,0.9,1.0,1.1 mm,装药尺寸均为0.6 mm×0.6 mm,空气隙的尺寸为Ф0.6 mm×0.6 mm; 结合爆炸网络安全间距,约为10 mm[13],设计控制通道的长度为10 mm。为提高单发测试元件实验的信息量,在每块网络试验件上设计了5个零门,通过固定控制通道长度,调整信息通道长度来控制信息通道与控制通道的传爆时间差。综合考虑网络安全间距、装药工艺和约束螺钉等限制条件,设计信息通道的长度分别为30,35,40,45,50 mm,根据装药爆速估计信息通道与控制通道时间差分别为2.5,3.0,3.5,4.0,4.5 μs。 图11含圆形空气隙改进零门的爆炸网络元件装药图 Fig.11Charge photo of explosive network component of improved null gate with round air groove 对所设计的网络试验件进行发火试验,零门正常作用下的爆炸效果图如图12所示。图12中各信息通道零门输出段(红色框线内)沟槽未扩展,仅由于爆轰振动造成装药飞溅,说明信息通道爆轰传播被阻断,所有零门均实现功能。不同间隙厚度的改进零门的试验结果见表4。 图12爆炸零门实验基板作用效果图 Fig.12Experimental basilar plate effect photo of explosive null gate 表4含圆形空气隙改进间隙零门试验结果 Table4Experimental results of improved gap null gate with round air groove signaltimedifference/μsgapthicknessH/mm0.60.70.80.91.01.12.5202020201403.0202020201633.5202020201974.0202020202084.520202020208 参照仿真结果可将表4中的数据分为三部分: (1)成功区域,即间隙厚度L≤0.9 mm,信息通道与控制通道时间差Δt≥2.5 μs时,零门均作用成功,符合仿真结果中间隙厚度L≤0.9 mm时零门关闭时间不超过0.9 μs的结论; (2)临界区域,即以1.0 mm为临界点构成的过渡区域,信息通道与控制通道时间差Δt≤4.0 μs时,开始出现部分失效,表明处于间隙厚度的临界状态时零门的关闭时间会快速增加,当两通道的设计时差不够大时即会导致关闭失败; (3)失效区域,间隙厚度超过1.1 mm时,关闭时间的大幅延长和冲击波的过度衰减会明显增加零门关闭失败的概率。此外,对比仿真与试验结果还可以看出,间隙厚度为1.0 mm、Δt≥0.9 μs时,仿真零门均成功作用,而实验中却发生部分失效; 间隙厚度为1.1 mm、Δt≤3.0 μs时,仿真零门均不能作用,而试验中却有部分成功。究其原因,主要是因为在数值模拟中装药尺寸、装药密度以及零门其它特征参量是一个确定值,而实际机械加工和装药工艺不可避免地存在一定的散差,因此在临界区域呈现出一定的差异性。因此,进行爆炸零门设计时应选择在成功区域,并尽量远离临界点,同时可以通过增加信息通道与控制通道的时间差,适度提高零门成功关闭的概率。 (1)针对装药尺寸0.6 mm×0.6 mm、圆形空气隙尺寸Ф0.6 mm×0.6 mm的爆炸改进零门进行了数值模拟,分析表明: 间隙厚度越小,到达信息通道装药的冲击波压力越大,零门结构破坏程度越高。在不超过网络装药临界起爆阈值的前提下,较小的间隙厚度有利于实现零门关闭功能。间隙厚度为0.6,0.7,0.8,0.9,1.0 mm时,零门的关闭时间分别为0.5,0.5,0.6,0.7,0.9 μs。间隙厚度为1.1 mm,零门不能实现其功能。 (2)参照仿真结果进行了部分试验验证,试验结果与仿真均符合较为一致的规律。当间隙厚度小于1.0 mm,信息通道与控制通道传播时间差Δt≥2.5 μs时,零门均能够实现功能,通过加大试验量,可进一步获得零门关闭的最小时差。当间隙厚度为1.0 mm时,零门的可靠性时间窗口为[4.0 μs,+∞); 当间隙厚度为1.1 mm时,即使信息通道与控制通道传播时间差大于4.0 μs,,零门的成功率依然较低。 (3)数值仿真能够为改进零门的机理分析和参数设计提供指导,但由于机械加工存在偏差等因素,确定性分析的数值仿真不能够完全代替试验,需进一步优化模型,开展零门关键参数随机性的仿真分析研究。 参考文献: [1] 周世罡, 李国新. 爆炸逻辑网络起爆控制系统研究[J]. 火工品,1999(1): 19. ZHOU Shi-gang, LI Guo-xin. Study on initiation control system of explosive logic network[J].Initiators&Pyrotechnics,1999(1): 19. [2] 温玉全. 刚性爆炸网络若刚应用研究[D]. 北京理工大学博士学位论文, 2000. WEN Yu-quan. Study on several applications of explosive logic circuit[D]. Beijing: Beijing Institute of Technology, 2000. [3] 李翔宇,范国庆,王马法,等. 一种基于拐角效应的新型爆炸零门试验研究[C]∥第六届全国爆炸力学实验技术学术会议论文集. 2010: 162-165. LI Xian-yu, FANG Guo-qing, WANG Ma-fa, et al. Experimental study on a new explosive null gate base on corer effect[C] ∥ The ninth national academic symposium on experimental technology of explosive mechanics. 2010: 162-165. [4] Meyers W H. On the design of explosive logic element[R]. LA-UR-84-392: 1984. [5] Courser D L. Explosive means: USA, 3095812[P]. 1963. [6] 罗华平, 黄亨建, 吴奎先, 等. 一种新型爆炸零门设计研究[J]. 含能材料, 2005, 13(增刊): 36-38. LUO Hua-ping, HUANG Heng-jian, WU Kui-xian, et al. Study on a new explosive logic null gate [J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2005, 13(Suppl.): 36-38. [7] 温玉全, 卢斌, 焦清介. 改进间隙式爆炸零门的设计及可靠性研究[J]. 火工品, 2001(4): 6-8. WEN Yu-quan, LU Bing, JIAO Qing-jie. The design of improving gap null gate and its reliability study[J].Initiators&Pyrotechnics, 2001(4): 410-413. [8] 黄海龙. 六分位爆炸逻辑网络设计及可靠性分析[D]. 北京理工大学硕士学位论文, 2006. HUANG Hai-long. The design and reliability analysis of six partite explosive logic circuit[D]. Beijing: Beijing Institute of Technology, 2006. [9] 李燕华, 李元, 李晓刚, 等. 一种间隙弱化爆炸零门的仿真和试验[J].含能材料, 2016, 24(10): 1005-1010. LI Yan-hua, LI Yuan, LI Xiao-gang, et al. Numerical simulation and experiment studies on weak gap explosive null gate[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2016, 24(10): 1005-1010. [10] 杨秀敏. 爆炸冲击现象数值模拟[M]. 合肥: 中国科学技术大学出版社, 2010. YANG Xiu-min. Numerical simulation of explosion shock[M]. Hefei: China University of Science and Technology Press, 2010. [11] Tarver C M, Urtiew P A, Chidester S K, ea.tl. Shock compression and initiation of LX-10[J].Propellants,Explosives,Pyrotechnics, 1993(18): 117-127. [12] 朱志武, 宁建国. Johnson-Cook冲击动态本构模型研究[C]∥2011年全国塑性力学会议论文集, 2011: 71-72. ZHU Zhi-wu,NING Jian-guo. Study on Johnson-Cook impact dynamic constitutive model[C]∥The 2011 National Academic Symposium on Plastic Mechanics, 2011: 71-72. [13] 李晓刚. 定向起爆用爆炸逻辑网络技术的若干研究[D]. 北京理工大学博士学位论文, 2008. LI Xiao-gang. Study on explosive logic network technology for directional initiation[D]. Beijing: Beijing Institute of Technology, 2008.
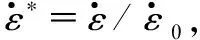

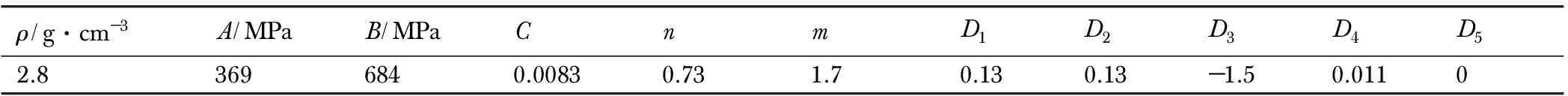
3.3 数值仿真结果





3.4 试验设计及研究


4 结 论
