构造双函数妙解导数综合题
2017-05-05
构造双函数妙解导数综合题
■广东省兴宁市第一中学 蓝云波
翻阅近十年各省市的高考题,就会发现大都以导数综合解答题作为压轴之作。这类题由于其解答的方法灵活,没有固定的解题套路,对同学们的综合能力要求较高,因此难度往往很大,得分率极低,在考试过程中导致不少同学对其“战略放弃”。因此,如何突破这一难点是同学们面临的一大难题。同学们平时若能多总结和反思,把解题的过程提升到一定的理论高度,自己的解题效率和能力将大大提升。通过对导数解答题的归纳分析,可以发现构造双函数是解答导数综合题的一大利器。
所谓构造双函数,即在解题过程中,只构造一个函数难以解决问题,甚至无法解决问题时,若能对问题进行等价转化,然后再构造两个函数,通过各个击破,可使问题得到最终解决。
下面以近几年的高考题和模考题为例,谈谈构造双函数在解答导数综合题中的应用。
一、求参数的取值范围
(2 0 1 5年河南省郑州市二模理科)已知函数f(x)=a x+l n(x-1),其中a为常数。
(1)试讨论f(x)的单调区间;
当a≥0时,f'(x)>0在定义域内恒成立,f(x)的单调递增区间为(1,+∞)。
当x∈(1,e)时,g'(x)>0,g(x)单调递增;当x∈(e,+∞)时,g'(x)<0,g(x)单调递减。
点评:求解此题的关键是通过对f(x)的最值的分析,拆去绝对值符号,然后再构造另外一个函数,对题意进行分析后,转化为最值大小关系的比较。问题的指向相对较为清晰,无需作过多的变形和等价转化。
二、研究方程的根的个数
已知函数f(x)=n+l nx的图像在点P(m,f(m))处的切线方程为y=x,设
(1)求m,n的值;
(2)求证:当x≥1时,g(x)≥0恒成立;
设φ(x)=x2-2 ex+t,x∈(0,+∞),则φ(x)=(x-e)2+t-e2。
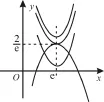
图1
所以函数h(x),φ(x)在同一直角坐标系的大致图像如图1所示。
点评:本题若直接构造一个函数,转化为研究函数的零点问题,显然难度较大,因为所要构造的函数极为复杂,难以使用导数这一工具,但在化为方程的根的个数的问题后,所需构造的两个函数便呼之欲出。
三、研究函数的图像的位置关系
解析:(1)函数的定义域为R。
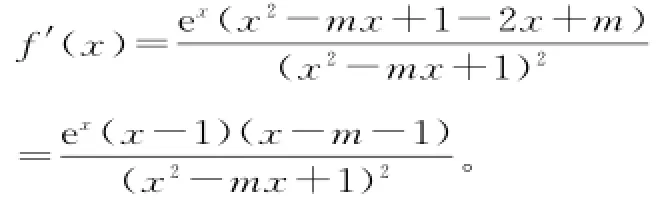
(1)若m∈(-2,2),求函数y=f(x)的单调区间。
(2)若
①当m+1=1,即m=0时,f'(x)≥0,此时f(x)在R上单调递增。
②当m+1>1,即0<m<2时,当x∈(-∞,1)时,f'(x)>0,此时f(x)单调递增;当x∈(1,m+1)时,f'(x)<0,此时f(x)单调递减;当x∈(m+1,+∞)时,f'(x)>0,此时f(x)单调递增。
③当m+1<1,即-2<m<0时,当x∈(-∞,m+1)时,f'(x)>0,此时f(x)单调递增;当x∈(m+1,1)时,f'(x)<0,此时f(x)单调递减;当x∈(1,+∞)时,f'(x)>0,此时f(x)单调递增。
综上所述,m=0时,f(x)在R上单调递增;当0<m<2时,f(x)在(-∞,1)和(m+ 1,+∞)上单调递增,f(x)在(1,m+1)上单调递减;当-2<m<0时,f(x)在(-∞, m+1)和(1,+∞)上单调递增,f(x)在(m+ 1,1)上单调递减。
(2)要证明函数y=f(x)的图像总在直线y=x上方,即证只需证。设g(x∈[0,m+1],则g(x)设令h'(x)=0,得x=1。
当x∈[0,1)时,h'(x)>0,h(x)单调递增;当x∈(1,m+1]时h'(x)<0,h(x)单调递减。所以当x=1时,函数h(x)取得最大值
点评:本题给出的参考答案极为复杂,使用的是极为复杂的分类讨论思想,在考场中要想顺利解答不是易事,但使用构造双函数的策略,则能化繁为简。
四、证明不等式
(1)求a,b;
(2)证明:f(x)>1。
解析:(1)函数f(x)的定义域为(0,+∞)。
设函数g(x)=xl nx,则g'(x)=l nx+
1
综上,当x>0时,g(x)>h(x),即f(x)>1。
点评:求解此题的困难之处在于同时含有指数、对数函数,只构造一个函数,最值难以求解。此时可考虑把式子分两端,构造双函数。除给出的解答之外,还可以变形为然后再构造双函数。需要特别指出的是,此题若不能证明[g(x)]min>[h(x)]max,不能说明f(x)>1不成立,因为所需证明的变量是同时取值,而双函数的最值未必在同一个x中取得。
(责任编辑 徐利杰)
