基于面板协整分析的外资与外贸关系研究
2017-05-04周玲张媛
周玲+张媛
[摘要]文章基于1984—2013年30年的外资与外贸数据,使用面板协整等面板时序方法对我国东、中、西部以及全国水平的外资与外贸关系进行了实证检验。实证结果表明,我国东、中、西部以及全国水平的外资与外贸之间存在长期稳定关系。从长期来看,全国层面和东部地区外资与外贸互为格兰杰因果关系;从短期来看,东部、中部和西部地区外资与外贸互为格兰杰因果关系。通过建立个体固定效应模型,可以得出外资对外贸有促进作用,但促进作用差异明显,东部促进作用最为明显,西部次之,中部最小。
[关键词]外资;外贸;面板协整;Granger因果关系
[DOI]1013939/jcnkizgsc201711282
1引言
改革开放以来,特别是20世纪90年代以后,我国从制度上,逐渐放宽了对外商投资的限制,再加上我国良好的经济发展形势,许多大型的投资公司纷纷进入我国投资,与之前相比,跨国公司投资规模有显著的提升,这就给我国带来了先进的经营战略、清晰的发展目标、多样的投资方式和深度的投资领域,特别是对我国进出口的促进作用发生了显著变化。从1984年到2013年,我国实际利用外资规模由126亿美元上升到118721亿美元,外贸总额由535亿美元上升到415899亿美元,外商直接投资与我国外贸呈现出双高增长的态势。2015年12月1日,人民币正式纳入SDR(特别提款权)货币篮子,这就意味着人民币已经成为全球主要储备货币之一,在国际市场上,人民币成为了真正意义上的“货币”,国际市场对人民币的认知大幅度地提升。加入SDR,成为了我国对外贸易和国际直接投资进一步发展的契机,二者之间的联系会进一步加强。那么在高速的经济发展过程中,我国的外资与外贸之间到底存在着怎样的关系,这是一个非常值得探讨的问题。
对外资与外贸关系的研究,国内外学者存在着两种截然相反的观点,第一种是以俄林(OhlinBG)与RA蒙代尔(RAMundell)[1]为代表的贸易替代论,该理论认为国家间生产要素禀赋的差异是其在国际间转移的根本原因,Beldelbos和Sleuwaegen(1998)、Brainard(1997)、Stone和Jeon(2000)等学者研究得出了相似的结论。第二种观点是以小岛清(KKojima)为代表的贸易互补论,该理论认为对外贸易和投资之间是相互补充关系。部分学者研究表明国际直接投资对外贸的单向促进作用,如陈继勇(1992)[2]、刘恩专(1999)[3]、邱立成(1999)[4]、谢冰(2000)[5]等。还有学者认为国际直接投资与外贸的双向促进關系,如崔春华(1993)[6]、向铁梅(2003)[7]、林鸾飞(2012)[8]等。
从前人的研究中可以得出这样的结论:在不同的时代背景下,直接投资与对外贸易之间的关系呈现不同的表现形式,所以不能简单地一言以蔽之,应该结合我国的实际情况进行分析。现有的研究主要存在以下的不足:第一是研究问题的角度缺失,现有研究的视角多是集中于外商直接投资流入国一方,从流出国视角进行的研究较少;第二是现有的研究多是使用传统的例如ADF、PP单位根检验等时序分析方法由于“势”过低,所以检验的结果缺乏稳健性,导致得出的结论可信度较低。
本文在获得我国东、中、西部各省数据的基础上,使用面板时序方法,对全国水平以及各区域的外资与外贸关系进行实证检验,以期得出更具稳健性的结论。
2实证分析
21数据说明
211数据来源
为了达到各区域之间进行对比的目的,文章以国家统计局口径为标准将中国分为东、中、西三个区域。由于西藏与青海获取的数据缺失值较多,因此本文的研究将这两个省份剔除。文章选取1984—2013年共30年的数据,选取各省份经营单位所在地进出口总额作为外贸指标,各省份实际利用外商直接投资金额作为外资指标。数据来源于《中国统计年鉴(2014)》和万德数据库。
212数据处理
首先,统一货币单位。只有统一了货币单位,数据之间才是可比的,这就需要利用各年度人民币与美元的汇率中间价,将两个变量的货币计量单位统一;其次,对变量进行不变价处理。使用固定资产价格指数对实际利用外商直接投资金额ZJTZ,使用消费价格指数对各省份经营单位所在地进出口总额JCK进行不变价处理,调整为以1984年价格的不变值;最后,对不变价格数值进行对数处理,分别记为LZJ和LJCK,这样做是为了降低异方差对建立的面板模型的影响。
22面板单位根检验
面板模型进行回归分析之前为了避免出现伪回归,保证结果的稳健性,对两个变量,即LZJ和LJCK水平及其一阶差分值进行全国水平及东部、中部、西部面板单位根检验。从检验的结果可以看出:不论是全国面板还是东部、中部、西部面板,对于LZJ和LJCK的水平值进行检验时,各变量检验的P值大于0100,故不能通过单位根检验,之后对LZJ和LJCK的一阶差分值进行检验时,各变量检验的P值均小于001,说明在1%的显著水平上,变量LZJ和LJCK的一阶差分序列为平稳序列。因此LZJ和LJCK均为一阶单整I(1)过程。
23面板协整检验
在通过面板单位根检验之后,需要做面板协整检验,这样做是为了判断变量LJCK与变量LZJ之间是否存在长期稳定联系。面板协整检验的原假设是“不存在协整关系”,即变量之间不存在长期稳定的联系,若检验的结果拒绝原假设,说明变量间存在长期的协整关系,这是建立面板模型必需的步骤。
检验结果表明:变量LJCK与变量LZJ长期均衡关系是存在的。除了东部与西部面板中Panel v-Statistic统计量不显著,全国、中部面板中Panel v-Statistic统计量在5%的显著水平下拒绝原假设,东部面板中统计量Group ADF-Statistic在10%的显著水平下拒绝原假设外,其他统计量均在1%的显著水平下拒绝原假设,综合来看,四个面板中两变量间均存在长期均衡关系。
24格兰杰因果检验
格兰杰(Granger)因果检验对于面板数据也是适用的,因为从本质上看,格兰杰因果检验是检验一个变量的滞后变量是否可以引入到其他变量方程中。一个变量如果受到其他变量的滞后影响,则称它们具有Granger因果关系。
检验结果表明:第一,在东部、中部和西部地区,从短期来看,外资与外贸之间互为Granger因果关系;第二,在全国和东部地区,从长期来看,外资与外贸互为Granger因果关系;第三,就全国水平来看,短期内外贸不是外资的Granger因果原因,但外资是外贸的Granger因果原因;第四,从长期来看,中部地区的外贸不是外资的Granger原因,但外资是外贸的Granger原因;第五,从长期来看,西部地区的外贸是外资的Granger因果原因,但外资不是外贸的Granger因果原因。
25面板协整方程估计
面板模型定义为:
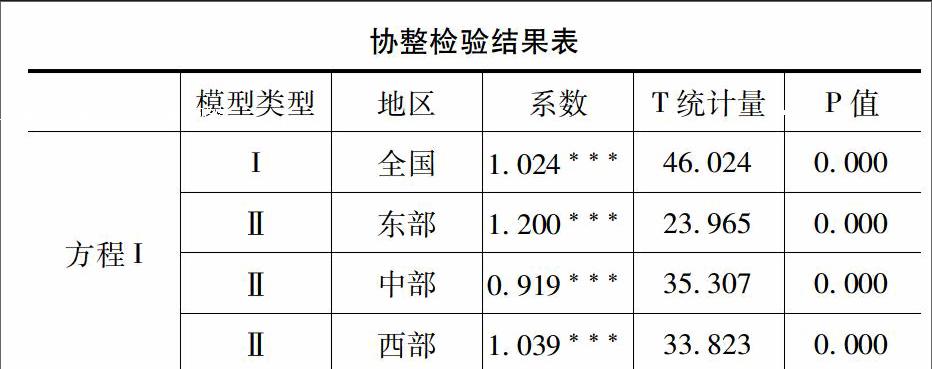
其中αi是随机变量,表示对于i个个体有i个不同的截距项,Yit为被回归变量,uit为误差项,Xit为k ×1阶回归变量列向量(包括k个回归量),β为k×1阶回归系数列向量,若αi且其变化与Xit有关系,称此模型为个体固定效应回归模型,若αi且其变化与Xit没有关系,则此模型为个体随机效应回归模型。协整检验结果见下表。
从模型估计系数的正负方向上来看,与之前的理论预期是一致的,全国水平以及各区域的外商直接投资对进出口都是发挥积极作用的。外商直接投资每增加1%,全国的进出口总额增长1024%,东部地区的进出口总额增长120%,中部地区的进出口总额增长0919%,西部地区的进出口总额增长1039%。东部、西部地区的增长水平高于全国平均水平,中部地区的增长水平低于全国平均水平,说明外商直接投资对进出口的促進作用是存在区域差异的。这主要是与我国的外资政策具有明显的地区倾向有关。
3结论
与世界上大多数国家一样,我国的经济发展也是有一个国际化的过程,在这个过程中,贸易首先成为经济稳定增长的动力。本文利用面板协整方法,使用1984—2013年近30年的省际面板数据,对我国外资与外贸关系进行了研究。研究结果表明:在全国以及东、中、西部水平上,外资与外贸之间存在着长期稳定的联系,这与之前根据现实情况做出的判断是相符合的。外商直接给我国经济发展带来了充足的资本,先进的技术水平,进而提高了我国的就业水平。面板模型估计的结果表明在四面板水平上,外商直接投资对于进出口贸易是起促进作用的,但由于各区域经济发展水平不同,所以这种促进作用存在明显的区域差异。相对于中、西部地区而言,东部地区吸收的外商直接投资对外商投资企业出口的促进作用更加明显,而中、西部外商直接投资对贸易的促进作用没有显著差别。
参考文献:
[1]Mundell R AInternational Trade and Factor Mobility[J].the American Economic Review,1957,47(3): 321-335
[2]陈继勇论战后美国海外直接投资对美国经济发展的影响[J].经济评论,1992(5):52-58
[3]刘恩专外商直接投资的出口贸易效应分析[J].当代经济科学,1999(2):65-70
[4]邱立成论国际直接投资与国际贸易之间的联系[J].南开经济研究,1999(6):33-39
[5]谢冰外国直接投资的贸易效应及其实证分析[J].经济评论,2000(4):30-35
[6]崔春华日本海外直接投资与贸易的关系[J].现代日本经济,1993(4):17-20
[7]向铁梅国际贸易与直接投资的关系及其中国情况的实证分析[J].世界经济研究,2003(3):14-19
[8]林鸾飞外商直接投资对出口贸易的影响研究[D].杭州:浙江工业大学,2012
[作者简介]周玲(1993—),女,山西晋中人,在读硕士研究生。研究方向:宏观经济统计分析;张媛(1995—),女,山西太原人,在读硕士研究生。研究方向:计量模型与应用。
