用老子思想建构生态式数学课堂的研究

陆珏琰

摘 要：老子认为“道”是世界的本源，世间一切事物都擁有其本身自然的发展规律，不应施加任何外力来改变其发展规律。在构建生态式数学课堂过程中，教师应结合老子思想，凸显学生的主体地位，遵循学生自身的认知规律，正视学生之间存在的个体差异。

关键词：老子思想；数学教学；生态课堂；主体地位

中图分类号：G623.5；B223.1 文献标志码：A 文章编号：1008-3561（2017）12-0076-01

中国文化博大精深，而阐释不尽的老子思想依旧吸引着源源不断的学者进行探索。教师将老子思想与教学方式相结合，打破一成不变的课堂教学模式，可以更快、更好地推动生态式教学课堂的发展。

一、“无为”，自主探究

在教学过程中，教师应该尊重学生的自身发展规律，凸显学生的主体地位。如在三年级“混合运算”的教学过程中，教师首先给学生提出问题：树林里一共有五排小树，第一排到第四排每排各有5棵树，第五排有7棵树，那么一共有几棵树？提出问题之后，教师让学生同桌两两进行讨论并举手给出自己的答案与算法。之后有两名学生给出以下答案：学生甲：一共有27棵树，因为5+5+5+5+7=27；学生乙：一共有27棵树，因为5×4+7=27。师：这两名同学给出的答案一样，但是给出的算式不一样，那么哪种算法更简单呢？学生：乙的算式更简单。之后教师又给学生提出几个类似的问题，并引导学生自己进行思考，不断地加深对混合运算的印象，增强学生使用混合运算知识的意识。因此，在教学过程中，教师应该尽量体现学生的主体地位，结合老子思想的“无为”，为教学方式做减法，通过“无为”而有所为，从而增强学生的自主探究意识与能力。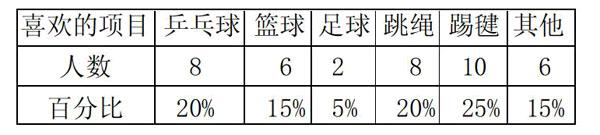

二、“不行”，循序渐进

在教学过程中，教师不能为完成教学任务而忽视学生自身的接受能力，在短时间内向学生灌输大量的新知识，让学生难以消化，甚至对数学学习产生抵触心理。如在六年级“扇形统计图”的教学中，教师先给学生布置了一项作业：统计全班同学喜欢的运动项目，并发给他们一张统计表。学生统计的结果如下表。

教师继续提问：如果用一张扇形图来表示这张表，我们应该怎么表示呢？此时学生都有些疑惑，于是教师在多媒体上现场做扇形图向学生更加直观地展示扇形图每一部分的含义。教师继续进行引导：乒乓球占20%代表着什么呢？我们把一个圆平均分成100份，20%说明乒乓球占其中的20份，依此类推各项目人数占全班人数的扇形图表示如右上图。

教师继续进行引导：大家看一看踢毽是不是最多的？再观察一下这张扇形图，是不是蓝色的踢毽部分占的面积最大？所以，今后再看到扇形统计图时，可以根据面积的大小判断数量的大小。大家现在还可以从这张图中发现什么呢？学生：喜欢足球的同学在我班占的人数是最少的。师：所以，我们学习的扇形统计图有什么优势呢？我们是不是可以更直接地观察到各项目人数在班级总人数之中所占的比例的情况？学生：是。通过这种学习方式，所有学生都更加深入地掌握了扇形统计图的应用。

三、“自然”，尊重差异

老子思想主张一切事物都有其自身的发展状态与规律，不应对其加以破坏。教师应该尊重学生之间存在的差异，耐心地发掘每一名学生的潜能，引导学生发现自己的长处，绽放自己的光彩。如在三年级“长方形和正方形面积的计算”的教学中，教师给不同的学生布置不同程度的作业。第一部分：在班级中成绩较差的学困生。针对这一部分学生，教师提出这样的问题：大家能比出你认为的1平方厘米、1平方分米、1平方米分别是多大吗？那么你知道怎么计算一个长方形或者正方形的面积吗？教师可通过这样简单的引导以及对旧知识的回忆，激发学生对新知识的兴趣。第二部分：学习努力但是成绩一直处于中游的学生。针对这一部分学生，教师可提出问题：你可以自己画一个面积是1平方厘米的正方形吗？你可以自己画一个面积是1平方厘米的长方形吗？有几种画法呢？教师可通过这样的问题让学生在探索答案的过程中建立自己的数学思维。第三部分：拥有自己的学习体系并且成绩优异的学生。针对这一部分学生，教师给出图形，并提出问题：图中红色长方形的长是2厘米，宽是1厘米。黄色正方形的边长与长方形的宽一样，那么这个组合图形的面积是多少？教师可通过这样的问题来提升这部分学生面对数学问题的引申能力。所以，在教学过程中，教师应该根据学生自身情况的不同为其提供不同的学习资源，让学生能够根据自身情况找到属于自己的学习方式，真正做到让学生学习不同的数学。

四、结束语

总之，教师结合老子思想进行数学教学，不仅能提升教学水平，而且也提升了自身的素质。同时，让学生根据自然发展规律成长、成才，也是建设生态式数学教学课堂的关键。

参考文献：

[1]杜亚丽.关于生态与生态课堂的解读[J].现代教育科学，2009（02）.

[2]余慧元，王定云.无——自由的哲学之维——老子“无”的思想研究[J].北京邮电大学学报：社会科学版，2003（01）.