基于连接成本的快递网络拥塞控制

杨从平，郑世珏，党永杰，杨 青

(1.广西民族大学商学院，广西 南宁 530006；2.华中师范大学计算机学院，湖北 武汉 430079)



基于连接成本的快递网络拥塞控制

杨从平1，2，郑世珏2，党永杰2，杨 青2

(1.广西民族大学商学院，广西 南宁 530006；2.华中师范大学计算机学院，湖北 武汉 430079)

本文采用图论的方法研究快递网络拥塞控制问题。通过分析快递网络流量特性，研究快递网络结构对网络传输能力的影响，平衡网络传输能力和连接成本之间的关系。首先，介绍介数的概念，考虑介数与货物流量的关系，修改了介数定义，并设计了介数的计算方法；接下来，根据介数计算公式推导快递网络传输能力与节点介数和节点能力的关系；然后，构建满足预期网络传输能力的最小连接成本拥塞控制模型，并设计了通过不断加边、重连和删除边的方法迭代寻找最优的快递网络结构；最后通过广西某快递公司的配送网络为算例验证模型和算法的有效性。研究结果显示算法能够有效地找出最优的快递网络，研究发现瓶颈节点的处理能力和介数决定网络的传输能力，网络传输能力与连接成本悖反。

快递网络；图论；拥塞控制；传输能力；连接成本

1 引言

近年来，随着电子商务的高速增长，与电子商务密切相关的快递业也呈现出欣欣向荣的蓬勃发展之势。然而我国快递业跟不上电子商务业迅猛增长的势头，成为电子商务供应链中的“瓶颈”[1]。快递企业在处理突然剧增的快件时，难以快速分拣和配送，造成大量快件在站点拥塞，甚至出现短时瘫痪的现象，给快递公司、电子商务企业和消费者带来了不同程度的影响。随着网络节点越来越多和网络流量的日益增长，快递网络拥塞问题变得越来越严重，导致配送时间的显著增加以及网络整体性能的急剧下降。如何有效避免拥塞，确保快递网络通畅具有重要的现实意义。

网络中存在一个临界值，当网络中待处理的数据包超过临界值，网络由自由流转向拥塞状态[2]。增加网络临界值则可以提高网络传输能力，目前学术界对提高网络传输能力的研究基本围绕着路由策略和网络结构两个方面展开。

目前路由策略的研究主要有全局、局部和混合型。1)在全局型路由策略研究方面，Yan Gang等[3]提出ER路由策略；Danila等[4]通过不断增加介数较高节点连接边的权重，使路径从最高介数节点调整到低介数节点；王开等[5]提出基于以节点度连乘积最小化的随机行走机理的优化路由策略；刘伟彦和刘斌[6]提出用节点的介数作为节点边的权重，加权网络最短路径的路由策略。2)在局部型路由策略研究方面，Wang Wenxu等[7]提出一种考虑邻居节点度的局部路由策略。3)混合型路由策略研究方面，Echenique等[8]提出综合考虑最短路径距离和邻居节点的等待时间的混合路由策略；Zhang Huan等[9]提出综合最短路径策略和邻居节点度信息的路由策略。

学者们在研究网络结构对网络传输能力的影响主要有提高链路或节点处理能力、删除链路、增加链路策略和链路重连等。1)提高链路或节点处理能力研究方面，Zhao Liang等[10]、Wu Zhixi等[11]、Ling Xiang等[12]、Zheng Jianfeng等[13]提出了节点或边的能力分配策略。2)删除链路策略方面，Liu Zhe等[14]提出了关闭具有连接度大的节点之间的链路；Zhang Guoqing等[15]提出了关闭具有较大介数节点之间的链路；张国清和程苏琦[16]提出了通过删除网络上的一些边，并把基于介数的基尼系数变化用于度量删边扩容的效果；蔡君和余顺争[17]提出一种通过逻辑关闭或删除对网络社团特性贡献度大的链路以提高网络传输性能的拓扑管理策略。3)增加链路策略，Newman和Girvan[18]、Huang Wei和Chow[19]提出了通过增加具有连接度较小的节点之间的链路以提高网络负载容量。4)链路重连策略，Jiang Zhengyuan等[20]采用随机重连、按度值重连和按介数重连三种方式研究对网络传输能力的影响。

学者们的研究成果为下一步研究打下良好的研究基础，然而学者们在研究提高网络传输能力时基本上没有考虑网络的连接成本，然而连接成本是不可忽略的。复杂网络如何精确控制、如何实行最小成本控制和如何选择最佳控制点，具有非常关键而且有着广泛科学意义和应用价值的研究问题[21]。基于此，本文考虑不同节点的处理能力约束，以最小化连接成本为优化目标对广西某快递公司的配送网络进行拥塞控制，目的是研究快递网络结构与快递网络传输能力的关系，为快递网络的拥塞分析和控制提供理论依据。

2 节点介数概念与介数的计算

2.1 介数的概念

介数的概念最早由Freeman[22]于1977年给出，并将介数分为节点介数和边介数两种，定义节点介数为最短路径通过某一节点的数目。用Bi表示节点i的介数，则Bi可以用式(1)来表示：

(1)

其中，V为网络节点的集合；如果起点为s终点为t的最短路经过节点i，则δ(s,i,t)= 1，否则δ(s,i,t)= 0。

根据Freeman对节点介数的定义，最短路径不包含节点i作为起点或终点的路径。本文为了更好地反映通过节点的货物流量，将通过节点i最短路径数量定义为包含节点i作为起点或终点的路径，则Bi可以用式(2)来表示：

(2)

其中，δ(i,j)表示起点为节点i的最短路径，δ(j,i)表示终点为节点i的最短路径。

假设快递流量及流向都均匀分布，且都是沿着最短路径流动，则可以用介数来反映相应的节点或者边流量大小，当节点或边的介数越大，通过的货物流量也会越多，节点和边就越繁忙。

2.2 将子网看成为含权重的节点的介数计算方法

为了降低为了算法复杂度，快速将关键节点的介数计算出来，可以快递网络的子网看成为含权重的节点，其权重等于子网的节点数目。如图1所示，将含有节点a的子网变成权重为7的节点，将含有节点b的子网变成权重为6的节点，将含有节点c的子网变成权重为5的节点。

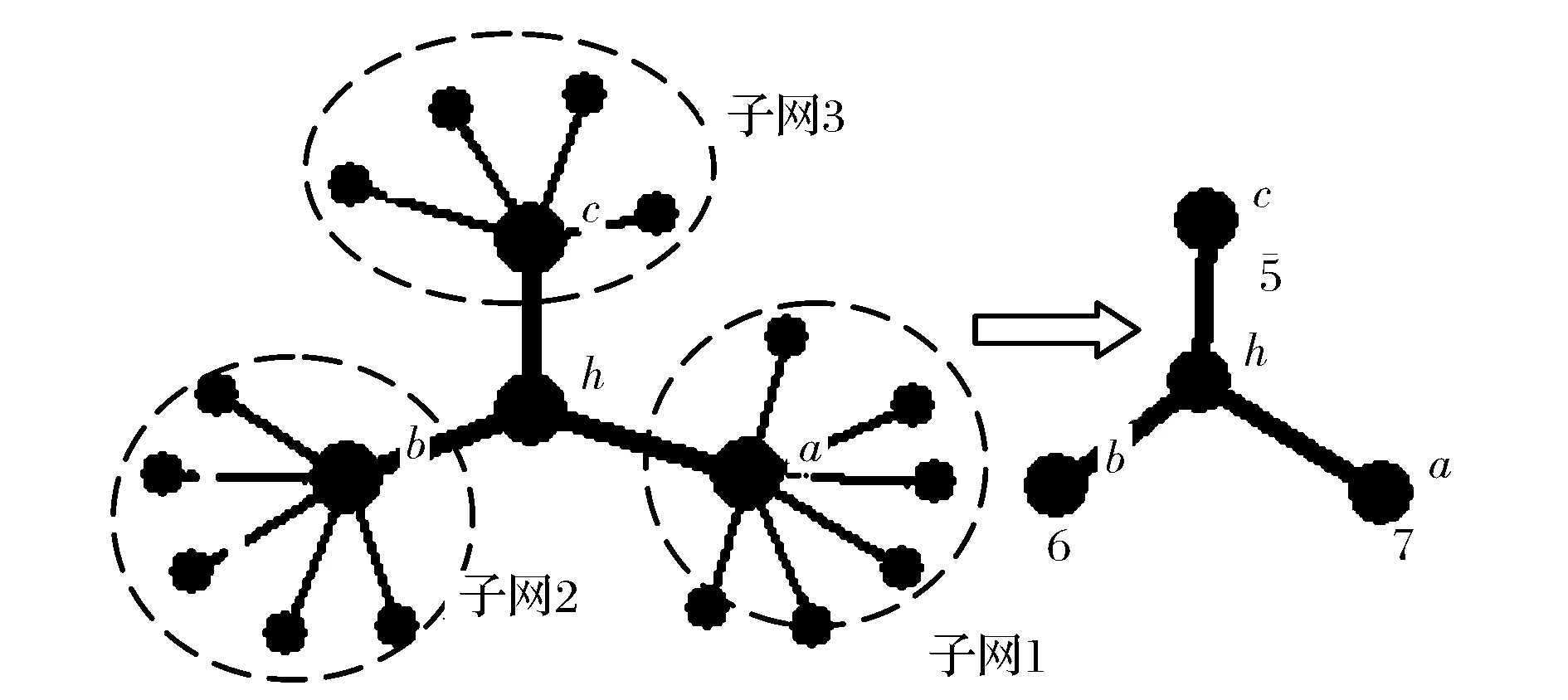
图1 将快递网络的子网看成含权重节点

以节点a为例分两步计算介数，第一步计算主干网络的最短路径通过节点a的数目，第二步计算子网内部通过节点a的最短路径，然后进行求和。

第一步计算主干网络中最短路径通过节点a的数目。首先求出主干网络中通过节点a的最短路径，然后再使路径上的节点的最短路径通过数目加上ki×kj(其中ki为最短路径起点的权重，kj为最短路径终点的权重)，如表1所示。在主干网络a→h→b的最短路径中，a的权重为7，b的权重为6，所以在主干网络a→h→b的最短路径中，通过节点a的最短路径数目为ki×kj= 7×6=42条。同样的方法可以计算出其他主干网络路径考虑起点和终点权重后通过节点a的最短路径数目，将表1中所有通过节点a的最短路径数目求和得到168条，168条最短路径数目为含节点a子网与子网外节点的最短路径通过节点a的数目。

表1 主干网络中最短路径通过节点a的数目

第二步计算子网节点之间通过节点a的数目，由于子网内的最短路径均需通过节点a，所以子网内部最短路径通过节点a的路径数目ki(ki-1)=7×6= 42条(ki为子网的节点数目)。

最后对两步计算的最短路径求和，得到通过节点a的最短路径为210条。

通过将子网看成为含权重的节点分两步计算主要目的是为了降低算法的复杂度，全局计算求最短路径的规模为整个网络，通过将子网看成为含权重的节点分两步计算可以将计算规模变为主干网络的节点数目。在规模较大的分层级的轴辐式快递网络中可以逐级把下一层级网络看成一个含权的节点，可以大大降低算法的复杂度，避免网络规模较大时节点的介数计算复杂度太大导致无法在有效时间计算出来。

3 快递网络传输能力

快递网络传输能力Rc是指快递网络在单位时间内能够处理的最大快递量，在单位时间内快递网络需要配送的快递量小于或等于Rc，快递网络处在自由流动的稳定状态；单位时间内快递网络中需要配送的快递量大于Rc，则快递网络从自由流状态转变为拥塞状态。

最容易产生拥塞的节点大多位于多条路径的交汇处，这些节点都具有相对较大的介数[23]。在节点规模为n的快递网络中共有n(n-1)条路径，假设每一快件随机地选择源节点和目标节点，则该快件通过节点i的概率Pi如式(3)所示：

(3)

其中，n为快递网络的节点数量，Bi为节点i的介数。

如果快递网络在单位时间内需要配送的快件数量为R，则通过节点i的快件数量Qi如式(4)所示：

(4)

反过来，如果已知节点i的快件数量Qi，则可知整个网络的配送的快件数量R如式(5)所示：

(5)

假设各节点的处理快件能力为ci，如果快递网络中任何节点的处理快件能力ci大于或等于通过节点的快递流量Qi，即min(ci-Qi) ≥ 0，则任何节点接收和发出的快件数量能够平衡，整个快递网络处于自由流状态；如果快递网络中存在某个节点的处理快件能力小余通过该节点的快递流量，即min(ci- Qi) < 0，产生的快件不能完全及时送达目标节点，在快递网络中就会出现拥塞。可见当min(ci-Qi) = 0时，快递网络处理的快递量R为最大网络传输能力Rc，则快递网络传输能力Rc可以如式(6)所示：

(6)

式(6)说明，快递网络整体传输能力不仅与节点介数有关，还与节点的处理能力有关。min(Ci×n(n-1) /Bi)的节点为瓶颈节点，由于n(n-1)为常量，即min(Ci/Bi)的节点为瓶颈节点，只需增加瓶颈节点的处理能力或使瓶颈节点的介数降低则可以提升快递网络整体传输能力。

4 优化模型建立及算法设计

4.1 优化模型

首先根据快递企业的需要给定快递网络一个期望网络传输能力，然后找出满足期望网络传输能力下的最优连接成本的网络结构，模型如式(7)和(8)表示：

f=min(sum(sum(A.×W)))

(7)

s.t.Rc≥RE

(8)

其中，A= (aij)n×n为网络G的邻接矩阵；W= (wij)n×n为网络G的距离权重矩阵；sum(sum( ))表示对矩阵的所有元素求和，即求快递网路的总连接成本Total_L；Rc为快递网络实际传输能力；RE为快递企业设定的期望快递网络传输能力。

式(7)为优化目标，使快递网络连接成本Total_L最小；式(8)为约束，要求快递网络必须满足期望的传输能力要求。

4.2 算法设计

算法设计从初始的轴辐快递网络开始，不断贪婪迭代寻找满足期望快递网络传输能力RE最低成本的网络结构，在每一次迭代中，进行一次加边操作、一次重新连边操作和一次删除边操作，每一次操作使更优的网络替代原来的网络，不断优化直到找到最优的网络结构为止，具体步骤如下：

步骤1 给期望快递网络传输能力RE赋值。

步骤2 根据网络G(V,L)求出邻接矩阵A，导入权重矩阵W。

步骤3 根据式(6)计算出初始网络的传输能力Rc，再根据G的邻接矩阵A和权重矩阵W计算出连接成本Total_L。

步骤4 令快递网络边数目m=n-1。

步骤5 加边操作。独立100次在快递网络G中随机添加一条边，记为Gi(i= 1,2,…100)，分别算出G1、G2、…、G100的连接成本Total_L1、Total_L2、…、Total_L100和网络传输能力Rc1、Rc2、…、Rc100。

步骤6 判断max(Rci)与Rc和RE关系，并进行选择操作。

①如果max(Rci)>RE，在Rci>RE的网络中找出满足max((Rci-RE)/(Total_Li-Total_L))的网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci，同时结束算法跳至第14步。

②如果max(Rci)=RE，在Rci=RE的网络中找出满足min (Total_Li-Total_L)的网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci，同时结束算法跳至第14步。

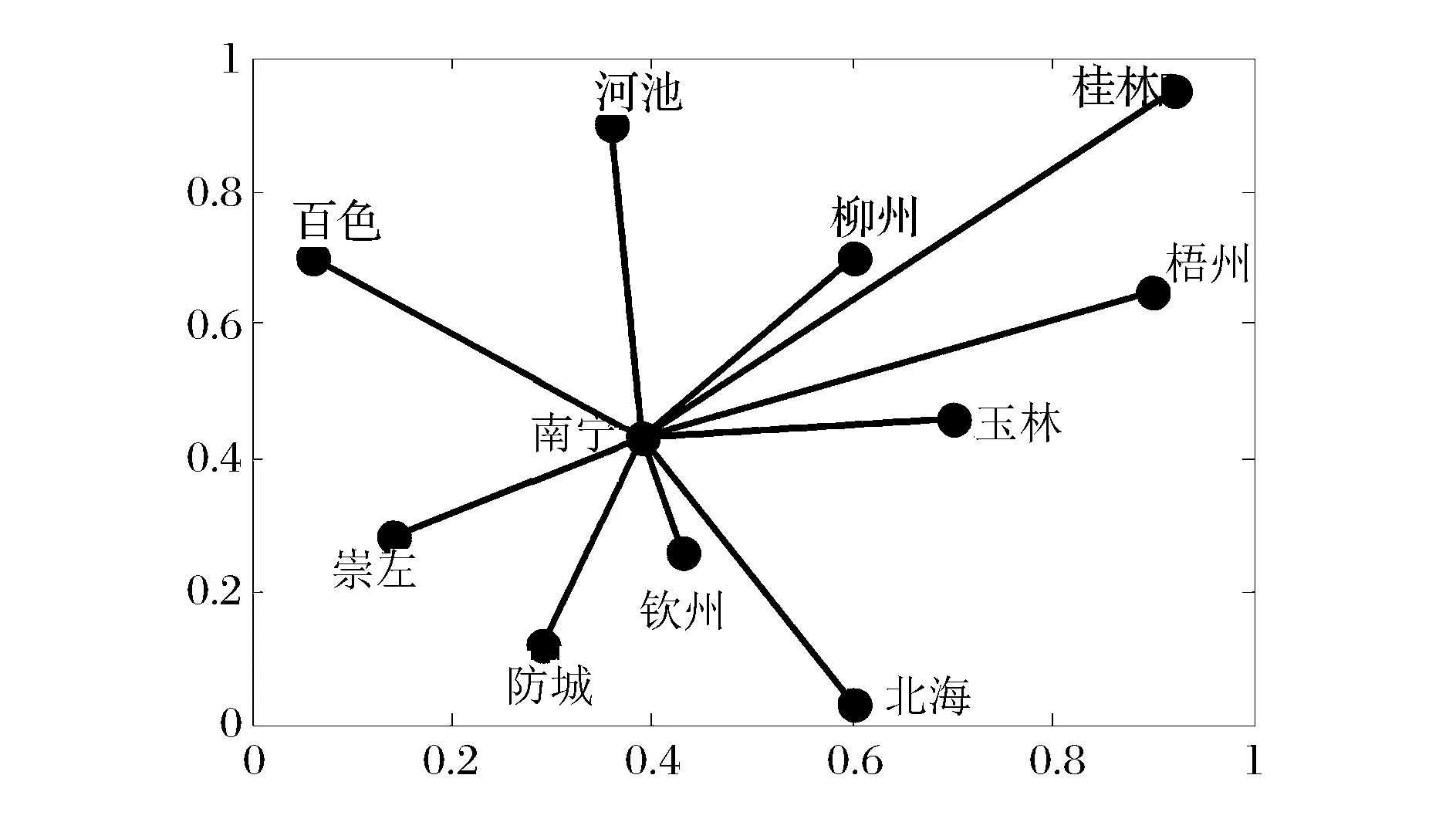
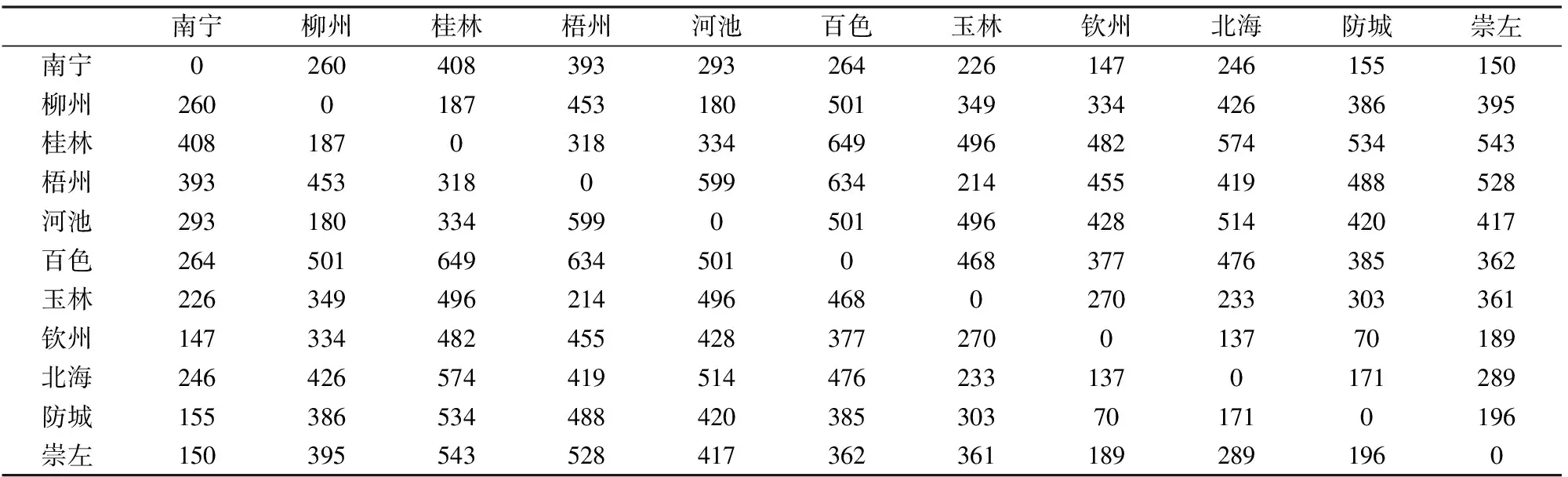
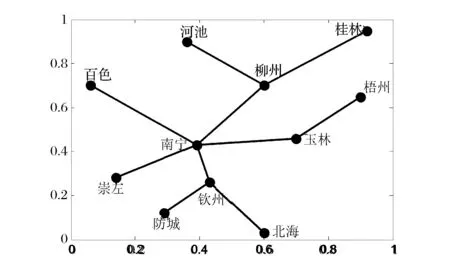
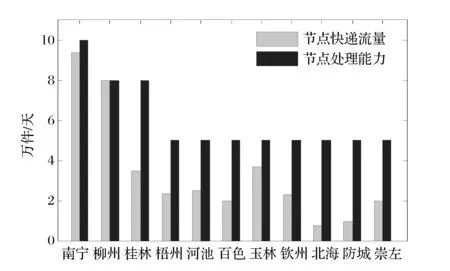
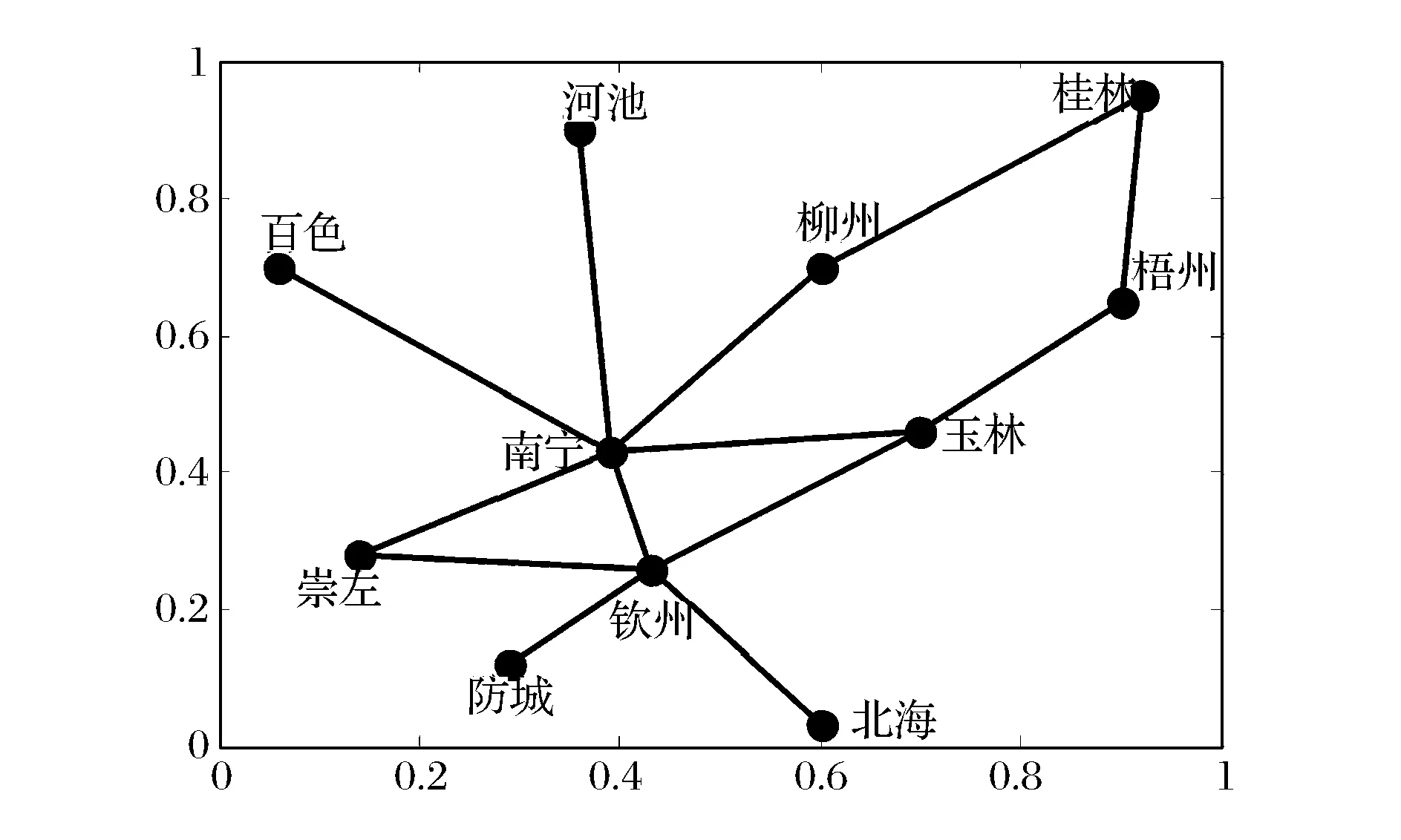
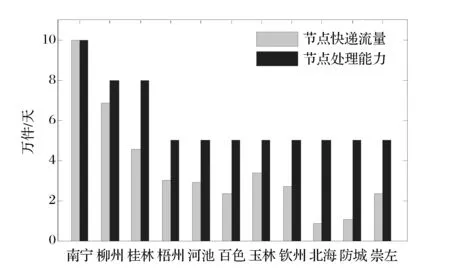
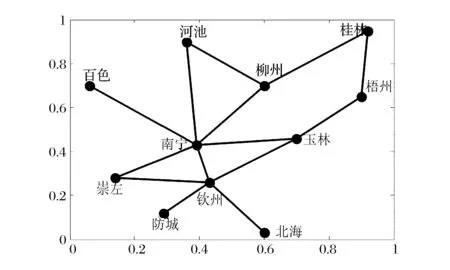
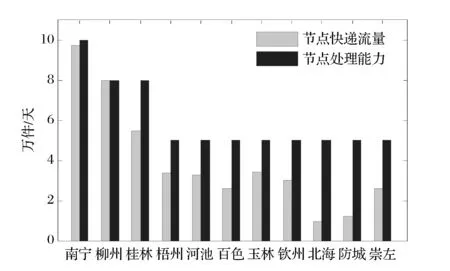
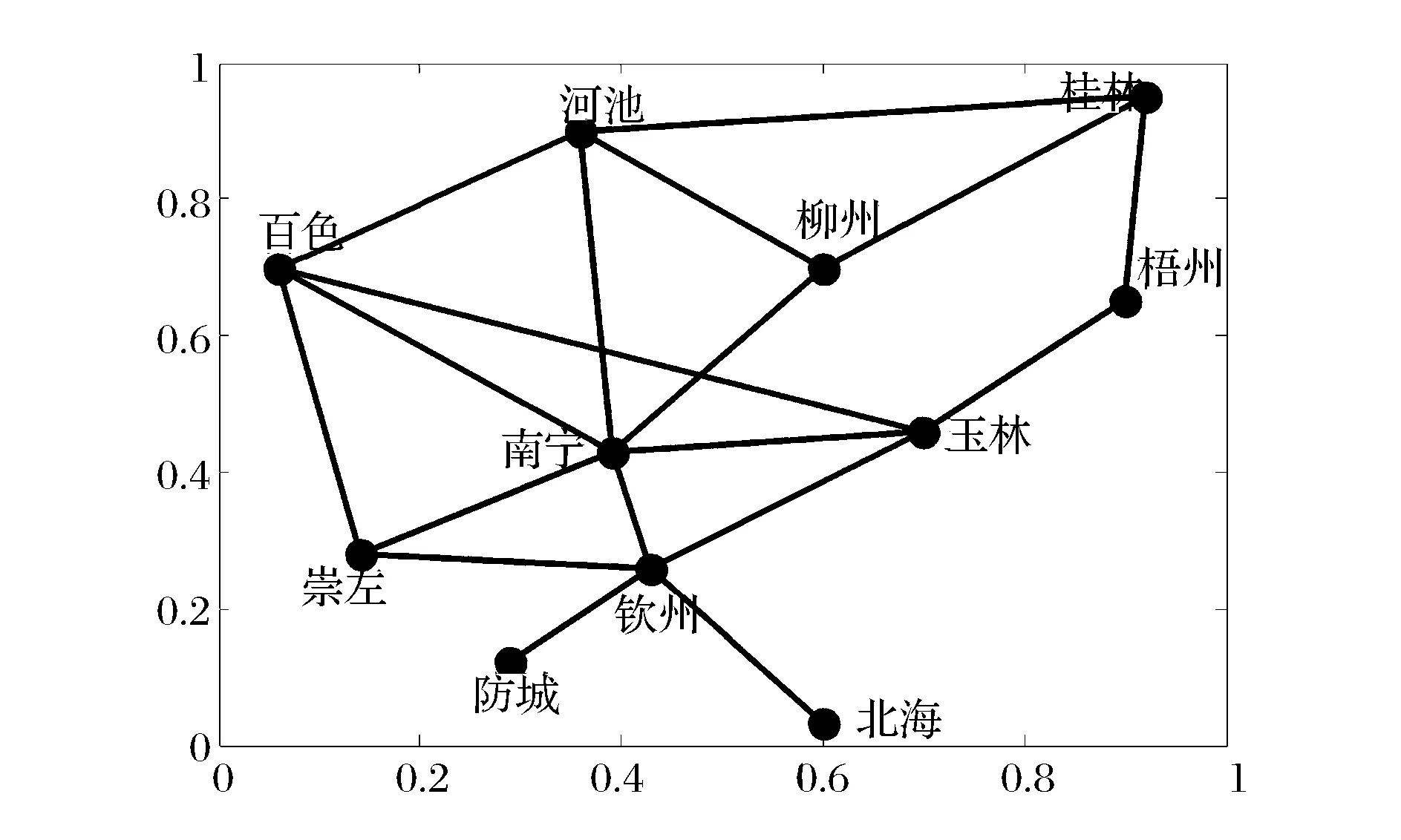
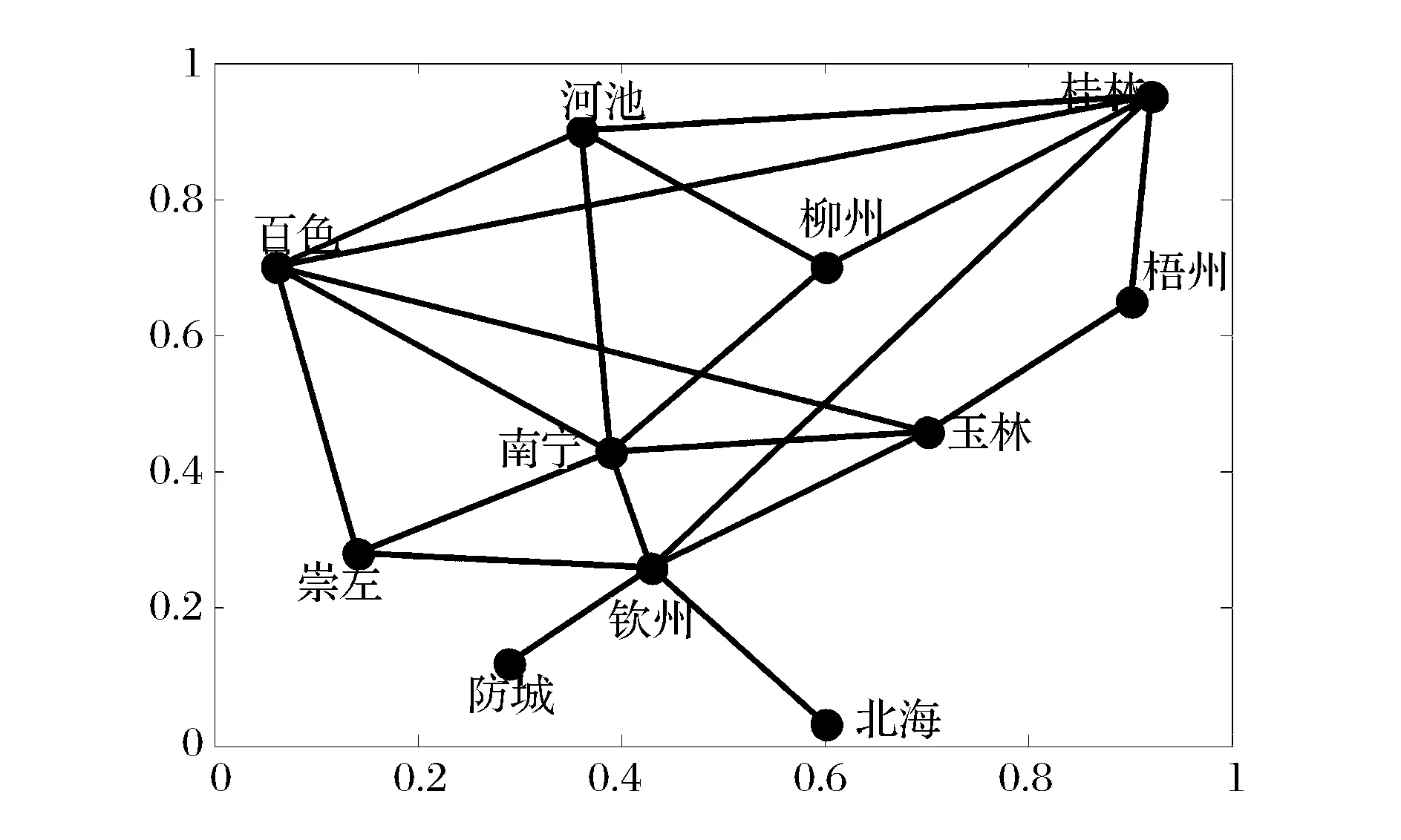
③如果Rc

④如果max(Rci)≤Rc，保持G、Rc和Total_L不变，令add= 0。

步骤7 判断是否满足m=n(n-1)/2，如果满足，结束算法跳至第14步，并输出“找不到满足条件的网络”。

步骤8 重新连边操作。找到网络中的瓶颈节点min(Ci/Bi)，删除一条与瓶颈节点相连接的边，然后独立100次在快递网络G中随机添加一条边(重新连接后保持快递网络连通)，记为Gi(i= 1,2,…100)，分别算出G1、G2、…、G100的连接成本Total_L1、Total_L2、…、Total_L100和网络传输能力Rc1、Rc2、…、Rc100。

步骤9 判断max(Rci)与Rc和RE关系，并进行选择操作。

①如果max(Rci)>RE

A、如果存在Rci>RE且Total_Li

B、如果不存在满足A，存在Rci>RE且Total_Li=Total_L的网络，在这些网络中找出max(Rci-RE)的网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci，同时结束算法跳至第14步。

C、如果不存在满足A或B，存在Rci>RE且Total_Li>Total_L的网络，在这些网络中找出max((Rci-RE)/(Total_Li-Total_L))的网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci，同时结束算法跳至第14步。

②如果max(Rci)=RE

A、存在Rci=RE且Total_Li

B、如果不存在满足A，存在Rci=RE且Total_Li=Total_L的网络，在这些网络中任意选择一个网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci，同时结束算法跳至第14步。

C、如果不存在满足A或B，存在Rci=RE且Total_Li>Total_L的网络，在这些网络中找出min(Total_Li-Total_L)的网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci，同时结束算法跳至第14步。

③如果Rc

A、存在Rc

B、如果不存在满足A，存在Rc

C、如果不存在满足A或B，存在RcTotal_L的网络，在这些网络中找出max((Rci-Rc)/(Total_Li-Total_L))的网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci。 ④如果max(Rci)=Rc

A、存在Rci=Rc且Total_Li

B、如果不存在Rci=Rc且Total_Li

⑤如果max(Rci)

步骤10 删除边操作。独立100次在快递网络G中随机删除一条边(删除边后保持所有节点连通)，记为Gi(i= 1,2,…100)，分别算出G1、G2、…、G100的连接成本Total_L1、Total_L2、…、Total_L100和网络传输能力Rc1、Rc2、…、Rc100。

步骤11 判断max(Rci)与Rc和RE关系，并进行选择操作。

①如果max(Rci)>RE，在Rci>RE的网络中找出满足max ((Rci-RE)/RE×(Total_L-Total_Li)/Total_L))的网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci，结束算法跳至第14步。

②如果max(Rci)=RE，在Rci=RE的网络中找出满足max(Total_L-Total_Li)的网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci，结束算法跳至第14步。

③如果Rc

④如果max(Rci)=Rc，在Rci=Rc的网络中找出满足max (Total_L-Total_Li)的网络Gi，并令G=Gi、Total_L=Total_Li、Rc=Rci，m=m-1。

⑤如果max(Rci)

步骤12 判断是否满足add= 0且reconnect= 0且delete= 0且Rc

步骤13 判断是否满足Rc≥RE，如果不满足，跳至第4步，进行下一次迭代。

步骤14 输出G、Total_L、Rc。

4.3 算法时间复杂度分析

计算所有节点介数的时间复杂度为O(D×n3)，D为网络最大跳数距离，每一迭代中进行加边、重连和删边操作都需要重新计算所有节点介数，假设最多需要迭代m次，则算法时间复杂度为O(m×3×D×n3)。由于网络的小世界特征，网络的最大跳数距离D一般都较小，所以算法复杂度为O(m×n3)。

由于整个快递网络节点规模较大，如顺丰速运目前在国内的营业网点有12000多个，如果直接对这个快递网络进行优化计算，其计算量非常庞大，无法在有效时间内完成计算。但由于快递网络是分层级的网络，可以采取分级优化，先对由一级枢纽节点组成的网络进行优化，然后对某一枢纽节点内的二级节点进行优化，直至末端配送节点。

5 算例分析

本文选择广西某快递公司进行拥塞控制，广西某快递公司的配送网络以南宁为枢纽节点，各地级市设有转运节点，各县设有末端配送点，除了极少数交通发达的乡镇外，大部分乡镇还没有布点，目前在广西共有142个节点。

5.1 数据

为了简化计算，本文只对由枢纽节点和转运节点组成的主干网络进行优化。主干网络为轴辐式结构，桂林、柳州、梧州、河池、百色、玉林、钦州、北海、防城港和崇左等10个转运中心以南宁为轴进行连接，主干网络如图2所示。主干节点间直达公路距离如表2所示，各主干节点分配的末端快递节点数目mi如表3所示。南宁节点的快件处理能力为10万件/天，柳州节点的快件处理能力为8万件/天，桂林节点的快件处理能力为8万件/天，其他主干节点的快件处理能力均为5万件/天。

图2 广西某快递公司主干网络结构

先通过式(6)对广西某快递公司初始轴辐式网络传输能力进行计算，得到传输能力Rc=11.15万件/天，网络连接成本Total_L=2342 km，瓶颈节点为南宁节点。

5.2 优化仿真结果

工作电脑为CPU主频2.1GHZ、内存2.0G的联想台式机， Matlab R2012a编程实现算法。

5.2.1 期望传输能力RE=12万件/天

设定期望传输能力RE为12万件/天，将数据输入Matlab程序，计算运行时间为37.166 s，得到快递网络传输能力Rc=12.501万件/天，网络连接成本为Total_L=1835 km，快递网络结构如图3所示。当快递网络的流量为12.501万件/天，各节点的快递流量如图4所示，柳州节点为瓶颈节点，其快递流量与其处理能力相等为8万件/天，其余节点的处理能力均大于通过快递流量，北海节点的能力利用率最低。

表2 节点间公路直达距离(单位：km)

数据来源：tool.2345.com

表3 各子网的节点数目

数据来源：广西某快递公司

图3 RE=12万件/天最低连接成本网络结构

图4 Rc=12.501万件/天各节点快递流量

5.2.2 期望传输能力RE=14万件/天

设定期望快递网络传输能力RE为14万件/天，程序计算运行时间为42.104 s，得到快递网络传输能力Rc=14.5703万件/天，网络连接成本为Total_L=2725 km，快递网络结构如图5所示。

图5 RE=14万件/天最低连接成本网络结构

当快递网络的流量为14.5703万件/天，各节点的快递流量如图6所示，瓶颈节点为南宁节点，南宁节点的快递流量与其处理能力相等为10万件/天，其余节点的处理能力均大于通过快递流量，北海节点的能力利用率最低。

图6 Rc=14.5703万件/天各节点快递流量

5.2.3 期望传输能力RE=16万件/天

设定期望快递网络传输能力RE为16万件/天，程序计算运行时间为48.710 s，得到快递网络传输能力Rc=16.3171万件/天，网络连接成本为Total_L=2905 km，快递网络结构如图7所示。

图7 RE=16万件/天最低连接成本网络结构

图8 Rc=16.3171万件/天各节点快递流量

当快递网络的流量为16.3171万件/天，各节点的快递流量如图8所示，瓶颈节点为柳州节点，柳州节点的快递流量与其处理能力相等为8万件/天，其余节点的处理能力均大于通过的快递流量，北海节点的能力利用率最低。

5.2.4 期望传输能力RE=18万件/天

设定期望快递网络传输能力RE为18万件/天，计算运行时间为62.093 s，得到快递网络传输能力Rc=18.3129万件/天，网络连接成本为Total_L=4570 km，快递网络结构如图9所示。

图9 RE=18万件/天最低连接成本网络结构

当快递网络的流量为18.3129万件/天，各节点的快递流量如图10所示，瓶颈节点为柳州节点，柳州节点的快递流量与其处理能力相等为8万件/天，其余节点的处理能力均大于通过快递流量，北海节点的能力利用率最低。

图10 Rc=18.3129万件/天各节点快递流量

5.2.5 期望传输能力RE=20万件/天

设定期望快递网络传输能力RE为20万件/天，程序计算运行时间为81.961 s，得到快递网络传输能力Rc=20.8187万件/天，网络连接成本为Total_L=5701 km，快递网络结构如图11所示。

图11 RE =20万件/天最低连接成本网络结构

当快递网络的流量为20.8187万件/天，各节点的快递流量如图12所示，瓶颈节点为南宁节点，南宁节点的快递流量与其处理能力相等为10万件/天，其余节点的处理能力均大于通过快递流量，北海节点的能力利用率最低。

图12 Rc=20.8187万件/天各节点快递流量

5.3 结果分析

本文假设快递流量及流向都均匀分布，且快递总是沿着最短的路径流动，通过分析及仿真，得到如下结果。

(1)瓶颈节点的处理能力和介数决定网络传输能力

瓶颈节点的处理能力和介数决定快递网络的最大整体传输能力Rc，快递企业可以通过改变瓶颈节点的处理能力和改变瓶颈节点的介数均可调节快递网络的传输能力。当改善瓶颈节点的的处理能力和介数后，瓶颈节点可能发生转移，如在轴辐网络中南宁节点为瓶颈节点，在期望快递网络传输能力RE=12万件/天的最低连接成本网络中瓶颈节点转移到柳州节点，只有不断寻找瓶颈节点并对其改善才能提升快递网络的整体传输能力。

(2)目前快递企业选择的轴辐式网络结构抗拥塞性能较差

目前广西某快递企业选择单枢纽纯轴辐式结构，其抗拥塞性能是较差的，因为所有的子网之间的路径均需通过枢纽节点，造成在枢纽节点的介数非常大。

(3)网络传输能力Rc与连接成本悖反

在节点处理能力不变的情况下，提高网络传输能力Rc则需提高快递网络的连接成本。为了节约网络连接成本，提高运营效果，快递企业应根据企业服务定位决定其传输能力。

6 结语

网络拥塞是各大快递企业常见的现象，有效避免拥塞，确保快递网络通畅具有重要的现实意义。本文采用图论的方法研究快递网络拥塞控制问题。提出一种考虑网络连接成本的快递网络拥塞控制方法，通过分析快递网络流量特性，研究快递网络结构对网络传输能力的影响，平衡网络传输能力和连接成本之间的关系。构建满足预期网络传输能力的最小连接成本拥塞控制模型，并通过不断贪婪迭代算法寻找满足期望快递网络传输能力最低连接成本的网络结构。仿真结果显示，该算法能有效地找出预期快递网络传输能力下的最低连接成本网络结构。

[1] 于宝琴，武淑萍，杜广伟. 网购快递物流服务系统测评的枝模型仿真[J]. 中国管理科学，2014，22(12)：72- 78.

[2] Arenas A, Díaz-Guilera A, Guimera R. Communication in networks with hierarchical branching[J]. Physical Review Letters, 2001, 86(14): 3196-3199.

[3] Yan Gang, Zhou Tao, Hu Bo, et al. Efficient routing on complex networks[J]. Physical Review E, 2006, 73(4): 046108-1—046108-5.

[4] Danila B, Yu Yong, Marsh J, et al. Optimal transport on complex networks[J]. Physical Review E, 2006, 74(4): 046106-1—046106-4.

[5] 王开，周思源，张毅锋，等. 一类基于随机行走机理的优化路由改进策略[J]. 物理学报，2011，60(11)：118903.

[6] 刘伟彦，刘斌. 基于加权路由策略的复杂网络拥塞控制研究[J]. 系统工程理论实践，2015，35(4): 1063- 1068.

[7] Wang W Xenxu, Wang Binghong, Yin Chuanyang, et al. Traffic dynamics based on local routing protocol on a scale-free network[J]. Physical Review E, 2006, 73(2): 026111-1—026111-7.

[8] Echenique P, Gómez-Gardees J, Moreno Y. Improved routing strategies for Internet traffic delivery[J]. Physical Review E, 2004, 70(5): 056105-1—056105-4.

[9] Zhang Huan, Liu Zonghua, Tang Ming, et al. An adaptive routing strategy for packet delivery in complex networks[J]. Physics letters A, 2007, 364(3-4): 177-182.

[10] Zhao Liang, Lai Y C, Park K, et al. Onset of traffic congestion in complex networks[J]. Physical Review E, 2005, 71(2): 026125-1—026125-8.

[11] Wu Zhixi, Peng Gang, Wong W M, et al. Improved routing strategies for data traffic in scale-free networks[J]. Journal of Statistical Mechanics: Theory and Experiment, 2008,(11): 1459-1475.

[12] Ling Xiang, Hu Maobin, Du Wenbo, et al. Bandwidth allocation strategy for traffic systems of scale-free network[J]. Physics Letters A, 2010, 374(48): 4825-4830.

[13] Zheng Jianfeng, Zhu Zhihong, Du Haoming, et al. Congestion and efficiency in complex traffic networks[J]. International Journal of Modern Physics C, 2013, 24(10): 1350072-1—1350072-12.

[14] Liu Zhe, Hu Maobin, Jiang Rui, et al. Method to enhance traffic capacity for scale-free networks[J]. Physical Review E, 2007, 76(3): 037101-1—037101-4.

[15] Zhang Guoqing, Wang Di, Li Guojie. Enhancing the transmission efficiency by edge deletion in scale-free networks[J]. Physical Review E, 2007, 76(1): 017101-1—017101-4.

[16] 张国清，程苏琦. 小世界网络中的删边扩容效应[J]. 中国科学：信息科学，2012，42(2)：151-160.

[17] 蔡君，余顺争. 一种有效提高无标度网络负载容量的管理策略[J]. 物理学报，2013，62(5)：058901.

[18] Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69(2): 026113-1—026113-16.

[19] Huang Wei, Chow T W S. Effective strategy of adding nodes and links for maximizing the traffic capacity of scale-free network[J]. Chaos, 2010, 20(3): 033123.

[20] Jiang Zhongyuan, Liang Mangui, An Wenjuan. Effects of efficient edge rewiring strategies on network transport efficiency[J]. Physica A: Statistical Mechanics and its Applications, 2014, 394: 379-385.

[21] 周涛，张子柯，陈关荣，等. 复杂网络研究的机遇与挑战[J]. 电子科技大学学报，2014，43(1)：1-5.

[22] Freeman L C. A set of measures of centrality based on betweenness [J]. Sociometry, 1977, 40(1): 35- 41.

[23] Barthelemy M. Betweenness centrality in large complex networks[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2004, 38(2): 163-168.

Congestion Control of Express Delivery Network Based on Connection Cost

YANG Cong-ping1,2, ZHENG Shi-jue2, DANG Yong-jie2, YANG Qing2

(1.College of Business, Guangxi University for Nationalities, Nanning 530006, China;2.School of Computer, Central China Normal University, Wuhan 430079, China)

By adopting graph theory，congestion control of express network is studied in this paper. Through the analysis of the characteristics of the network traffic flow and the study on the effect of the structure of express network on the network transmission capability, balancing the relationship between the network transmission capability and the connection cost. First of all, the concept of betweenness is introduced. Considering the relationship between the betweenness and cargo flow, the betweenness definition is modified, and the calculation method of betweenness is designed. Next, according to the betweenness calculation formula, the relationship of express network transmission capacity, node betweenness and node capacity are derived. Then, by taking the minimum connection cost as the optimization goal, an optimization model of express delivery network with the constraint of expect transmission capacity is constructed, and an algorithm is designed to seek the network with the optimal structure by gradually adding edge, reconnecting edge and deleting edge. Finally, the example of the backbone network of an express delivery company in Guangxi province is taken to verify the effectiveness of the model and algorithm. The result of simulation indicates that the algorithm can effectively find out the optimal delivery network. Through the research, it is found that processing power and betweenness of the bottleneck node decision network transmission capacity, and there is a contradiction between network transmission capacity and connection cost.

express network; graph theory; congestion control; transmission capacity; connection cost

2015-06-24；

2015-12-18

国家自然科学基金资助项目(61170017)

杨从平(1975-)，男(苗族)，广西资源县人，广西民族大学商学院副教授，博士，研究方向：物流网络，E-mail:1007843722@qq.com.

1003-207(2017)04-0143-09

10.16381/j.cnki.issn1003-207x.2017.04.017

F252.3

A