随机加权自适应滤波及其在组合导航中的应用
2017-05-03阎海峰魏文辉赵雪华高朝晖高社生
阎海峰, 魏文辉, 赵雪华, 高朝晖, 高社生
(西北工业大学自动化学院, 西安 710072)
0 引言
Kalman滤波[1]是一种线性最小方差估计,其显著特点是对状态空间进行估计。但Kalman滤波要求准确已知系统的数学模型、系统噪声和量测噪声的统计特性,而工程实际中系统模型和噪声特性一般是部分已知、近似已知或者完全未知的。在这种情况下,采用对系统噪声和量测噪声进行有限记忆在线计算的自适应滤波方法进行计算效果较好。该算法是一种自适应滤波算法,在量测噪声未知或不准确时,通过对新息残差序列的检测,利用统计方法得到量测噪声阵的无偏估计。
到目前为止,人们已提出了各种自适应卡尔曼滤波方法,其中比较有代表性的方法有:噪声有限记忆在线计算自适应滤波算法、渐消记忆自适应滤波算法和带未知时变噪声估值器的Sage-Husa自适应滤波[2-3]。
为了进一步提高自适应Kalman滤波的估计精度和速度,基于Sage滤波的思想,一些学者提出了移动开窗自适应估计方法,即在选定的窗口内,采用对残差向量求平均值的方法,实时在线估计当前时刻系统的噪声统计性质[4-8]。由于该方法计算简单,且能达到一定的估计精度,因此该方法被用于估计并拟合观测系统模型误差和动力学系统模型误差。
随机加权法[9-13]是一种新兴的统计计算方法。该方法有许多优点,如估计是无偏的、计算简单、不需要知道参数的准确分布、适合于大样本的计算。然而,截至目前,将随机加权方法用于噪声有限记忆的自适应滤波计算的研究未见报道。
文中提出一种噪声有限记忆在线随机加权自适应滤波算法,在该算法中,将移动开窗技术和随机加权估计相结合,利用移动开窗方法求得系统量测噪声和系统状态噪声的统计特性,再利用随机加权方法分别对系统量测噪声和状态噪声的统计特性进行在线随机加权估计,并根据误差大小,对随机加权自适应因子对其进行调节,控制系统量测噪声和状态噪声对滤波解算精度的影响。仿真结果表明,在系统噪声统计未知情况下,所提出的噪声有限记忆在线随机加权自适应滤波算法精度明显优于传统的Sage自适应Kalman滤波算法。
1 随机加权估计
设X1,X2,…,Xn是独立同分布(iid)的随机变量序列,总体分布为F(x),相应的经验分布函数为:
(1)
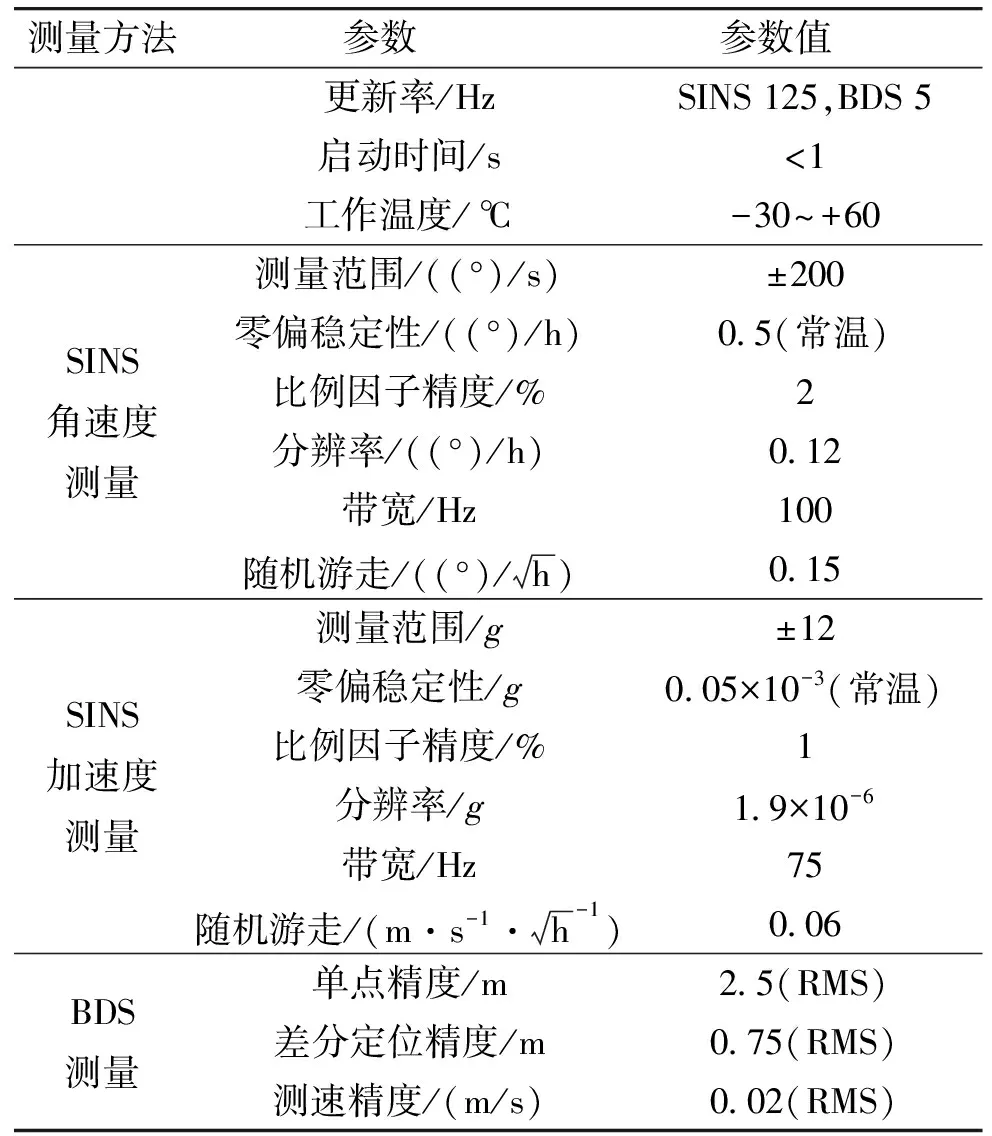
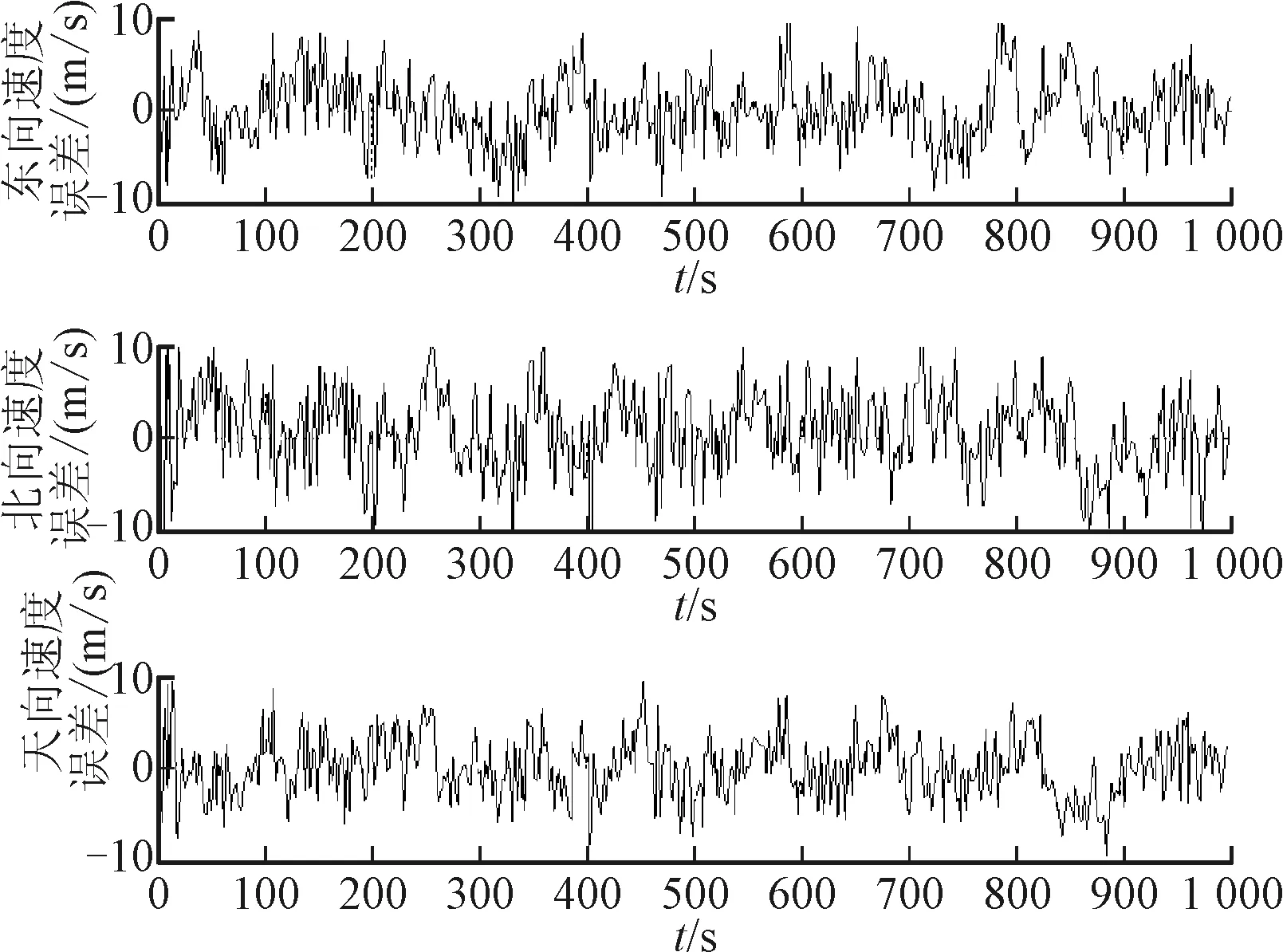
其中Ι(Xi Fn(x)的随机加权估计定义为: (2) 其中随机向量(v1,…,vn)服从Dirichlet分布D(1,1,…,1),即并且(v1,v2,…,vn-1)的联合分布密度为f(v1,v2,…,vn-1)=Γ(n)。其中(v1,v2,…,vn)∈Dn且 卡尔曼滤波的基本方程为: (3) 状态一步预测方程: (4) 状态估值计算方程: (5) 滤波增益方程: (6) 式中,Pk|k-1是一步预测均方误差阵。 一步预测均方误差方程: (7) 估计均方误差方程: (8) 或 Pk=(I-KkHk)Pk|k-1 (9) 上面公式中,式(4)和式(7)又称为时间更新方程,其余3个方程又称为量测更新方程。 假定系统状态方程为: Xk=Φk,k-1Xk-1+Γk-1Wk-1 (10) 量测方程为: Zk=HkXk+Vk (11) 这里的系统噪声W和量测噪声V的统计特性未知,将其表示为未知时变统计参数,并且满足E(W)=q,E[(W-q)(W-q)T]=Q,E(V)=r,E[(V-r)(V-r)T]=R。 下面对未知时变参数q、Q、r、R进行在线估计。假设在给定时刻tk,系统量测满足式(11),即Zk=HkXk+Vk。其中Zk和Vk均为m×1维向量,且设Vk~N(r,R)。 由于Xk和Vk未知,由下式可给出Vk的近似值: rk≈Zk-HkXk/k-1 (12) 式中:rk被称为量测残差向量,{rk}为一个均值为零的白噪声量测残差向量序列,其方差为: (13) 假定Vk(k=1,…,N)互不相关,而且统计量r和R为常值,则量测噪声采样值rk(k=1,…,N)落入由{Vk}张成的空间ΩR内。在空间ΩR内定义一个随机变量,其均值为r,方差为Cr。基于空间ΩR内得到的噪声采样值rk(k=1,…,N),则系统量测噪声向量V的均值r的算术平均无偏估计为: (14) 方差Cr的算术平均无偏估计为: (15) (16) 则R的算术平均无偏估计为: (17) 相应地,r的随机加权估计为: (18) Cr的随机加权估计为: (19) (20) 则R的随机加权估计为: (21) 假设在给定时刻tk,系统状态满足式(10),即Xk=Φk,k-1Xk-1+Γk-1Wk-1,这里Xk为n×1维向量,Wk为p×1维向量,并设Wk~N(q,Q)。 由于Xk和Xk-1的真实值未知,故Wk未知,但可由下式给出Wk的近似值qk,即: (22) 假定Wk(k=1,…,N)互不相关,而且统计量q、Q为常值,则系统噪声采样值qk(k=1,…,N)落入由{Wk}张成的空间ΩQ内。在空间ΩQ内定义一个随机变量,其均值为q,方差为Cq。基于空间ΩQ内得到的噪声采样值qk(k=1,…,N),可以得到q的算术平均无偏估计为: (23) 方差Cq的算术平均无偏估计为: (24) Q的算术平均无偏估计为: (25) 相应地,系统噪声向量W的均值q的随机加权估计为: (26) 同前所述,下标k表示第k时刻。 方差Cq的随机加权估计为: (27) Q的随机加权估计为: (28) 从以上分析可知,基于N个量测噪声采样值rk(k=1,…,N)和N个系统噪声采样值qk(k=1,…,N),可以得到量测噪声与系统噪声统计量q、Q、r、R的无偏估计。 将噪声统计特性的有限记忆在线估计与卡尔曼滤波基本方程相结合,则可得到噪声统计有限记忆自适应滤波算法。 3.1.1 系统状态方程 建模中的BDS均指BDS-2,建模的导航坐标系选为地心固连坐标系(ECEF)。MEMS IMU/BDS深组合导航系统的状态量由MEMS IMU与BDS的状态误差向量组成: X=[XIMUXBDS]T (29) 则系统状态方程为: (30) 式中:FIMU是状态向量XIMU的系数矩阵;FBDS是状态向量XBDS的系数矩阵;XIMU为与IMU相关的误差向量;XBDS为与BDS相关的状态误差向量;WIMU和WBDS分别为状态量XIMU和XIMU的噪声向量;AIMU和ABDS分别是WIMU和WBDS的系统噪声矩阵;XIMU由位置误差向量、速度误差向量、姿态误差向量和加速度计误差及陀螺漂移引起的误差构成。即: (31) 式中:δr是三维位置误差向量;δv是三维速度误差向量;δφ是3个失准角向量;ε和Λ分别表示陀螺和加速度计偏置的随机分量,并认为是有色噪声,常用一阶马尔可夫过程表示。 3.1.2 系统量测方程 则第i颗北斗卫星的量测量Zi可表示为: (32) 3.2.1 试验目的 为了验证文中提出的噪声有限记忆在线随机加权自适应滤波算法在工程实际应用中的可行性和应用效果,将提出的算法应用于BDS/MEMS IMU深组合导航系统中进行实际跑车试验,并与Sage自适应Kalman滤波进行比较。 所用BDS/MEMS IMU深组合导航系统传感器参数如表1所示。 表1 BDS/MEMS IMU深组合导航系统传感器参数指标 3.2.2 试验过程 试验开始时,对BDS/MEMS IMU深组合导航系统经过1 min初始化,然后沿环山路向东行驶,经过沣峪口转盘掉头回到初始位置,行车时间约21 min,总里程约12.46 km,平均行驶速度37.2 km/h,车辆行驶稳定,行车轨迹如图1所示,对应的位置坐标如图2所示,其中起始点纬度N34°1′41″,经度E108°46′5″,掉头点纬度N34°3′10″,经度E108°49′4″。试验过程中,BDS观测环境良好,平均可接收到8颗导航星信号。高精度广域差分系统输出的位置参考信息,与试验数据一起由数据存储器采集获得,后处理过程中用于滤波解算和算法性能验证。 图1 跑车试验轨迹图 图2 行车轨迹位置坐标图 3.2.3 试验数据处理及结果分析 图3 Sage自适应Kalman滤波算法的位置误差 图4 随机加权自适应滤波算法的位置误差 图5 Sage自适应Kalman滤波算法的速度误差 选取试验时间为1 000 s的数据用于滤波处理,滤波周期0.1 s,传感器参数如表1所示。分滤波算法估计误差结果如图3~图6和表2所示。由试验结果可知,在实际应用中,Kalman滤波对于系统模型和噪声统计特性的近似假设必然会带来较大的估计误差,尽管Sage自适应Kalman滤波通过移动开窗自适应估计方法对系统模型误差和动力学系统模型误差进行了拟合,但对噪声统计特性的估计精度有限,因此最终达到的估计精度并不理想,其位置估计精度只能维持在10 m以内(位置RMSE 2.83 m),速度估计精度维持在0.2 m/s以内(速度RMSE 0.067 m/s)。 提出的噪声有限记忆在线随机加权自适应滤波算法,将移动开窗技术和随机加权估计相结合,不仅对系统量测噪声和状态噪声的统计特性进行在线随机加权估计,而且根据误差大小,利用随机加权自适应因子对其进行调节,控制系统量测噪声和状态噪声对滤波解算精度的影响,因此,其位置估计精度能达到3.5 m以内(位置RMSE 1.12 m),速度估计精度达到0.1 m/s以内(速度RMSE 0.029 m/s)。 图6 随机加权自适应滤波算法的速度误差 表2 滤波算法估计误差统计 在系统噪声统计未知情况下,所提出的噪声有限记忆在线随机加权自适应滤波算法精度明显优于传统Sage自适应Kalman滤波算法。 参考文献: [1] 付梦印, 邓志红, 张继伟. Kalman滤波理论及其在导航系统中的应用 [M]. 北京: 科学技术出版社, 2003: 8-35. [2] 杨元喜. 自适应动态导航定位 [M]. 北京: 测绘出版社, 2006: 136-141. [3] SAGE A P, HUSA G W. Adaptive filtering with unknown prior statistics [C]//IEEE Joint American Control Conference. [S.l.]:IEEE,1969: 769-774. [4] YANG Y, XU T. An adaptive Kalman filter based on Sage windowing weights and variance components [J]. The Journal of Navigation, 2003, 56(2): 231-240. [5] GAO S S, WEI W H, ZHONG Y M, et al. Sage windowing and random weighting adaptive filtering method for kinematic model error [J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1488-1500. [6] YANG Y, ZHANG S. Adaptive fitting for systematic errors in navigation [J]. Journal of Geodesy, 2005, 79(1/2/3): 43-49. [7] YANG Y, ZHANG S. Fittings of systematic errors and covariance matrices in navigation [J]. Acta Geodaetica Et Cartographic Sinica, 2004, 33(3): 189-194. [8] ZHONG Y M, GAO S S, WEI W H, et al. Random weighting estimation of kinematic model error for dynamic navigation [J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 2248-2259. [9] ZHENG Z G. Random weighting method [J]. Acta Mathematicae Applicatae Sinica, 1987, 10(2): 247-253. [10] GAO S S, GAO Y, ZHONG Y M, et al. Random weighting estimation method for dynamic navigation positioning [J]. Chinese Journal of Aeronautics, 2011, 24(3): 318-323. [11] GAO S S, FENG Z H, ZHONG Y M, et al. Random weighting estimation of parameters in generalized Gaussian distri-bution [J]. Information Sciences, 2008, 178(9): 2275-2281. [12] GAO S S, ZHANG Z L, YANG B. The random weighting estimate of quantile process [J]. Information Science, 2004, 164(1/2/3/4): 139-146. [13] GAO S S, ZHONG Y M, LI W. Random weighting method for multi-sensor data fusion [J]. IEEE Sensors Journal, 2011, 11(9): 1955-1961.2 噪声有限记忆在线随机加权自适应滤波算法
2.1 卡尔曼滤波简介

2.2 量测噪声统计特性的在线估计
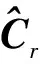

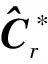
2.3 系统状态噪声统计特性的在线估计
3 实验分析
3.1 MEMS IMU/BDS深组合导航系统数学模型

3.2 跑车试验