不同类型导弹间智能协同目标分配方法研究

何广军, 卜祥伟, 吴建峰, 赵 岩

(空军工程大学防空反导学院, 西安 710051)

0 引言

传统意义上的防空导弹,在对付目标饱和攻击时,通常采用连射或者齐射方式,但在导弹发射后,同一武器系统以及不同武器系统发射的导弹间均是独立攻击目标,相互间没有数据交换和协同。文中针对防空导弹武器系统的特点,提出一种通过制导站实现不同类型导弹间的数据交换和协同目标分配的方法,通过改进的萤火虫优化算法对协同攻击目标时的目标分配做了研究。

1 协同攻击的数据交换方法

实现导弹间协同攻击,首先要解决的是导弹间的数据交换问题。在防空导弹飞行过程中,要实现导弹间的直接无线通信,由于导弹的机动飞行,需要弹上的收发天线的方向图达到360°围绕弹体的全覆盖。具备这样功能的天线需要在弹体表面至少各180°方向布置两套天线系统,对弹上发射机的功率及处理信号的能力也提出了很高的要求。对于高机动飞行的防空导弹而言,很可能由于弹体的遮挡、发射功率的限制等达不到预期的目的。特别对于不同类型的导弹的协同数据交换,由于导弹对信息处理能力的限制,数据格式的互异性,相互间的数据交换会变得异常困难。

一种可行的方案是通过制导站中继实现导弹间的通信的方法。该方案的实质是对已有防空作战单元之间以及制导站与导弹间的数据交换完成数据链的改造。对于目前大多采用复合制导方式的导弹,在导弹发射后,通常制导站还要与导弹之间有不间断的数据传输。这些数据包括了弹道修正指令、引信开机、导弹自毁指令和导弹的应答信号等,另外,现有的武器系统已经实现了不同防空作战单元之间的联网作战。基于上述已有的数据交换和联网作战功能,对其数据交换方式和联网作战进一步扩展,通过制导站的中继作用,实现导弹与导弹之间数据链交换是可行的。文献[1]虽然对导弹之间的机动及如何具体实现未做深入研究,但通过仿真对弹上采用直扩数据链和跳频数据链两种弹载数据链进行了研究,间接验证了采用通过制导站中继完成导弹间数据链通信的可行性。

通过制导站中继完成导弹间的通信,进而实现导弹间的协同拦截目标,同以往在导弹发射前就完成目标分配的方式不同,这种方式完成了导弹飞行过程中的联网;可以充分利用制导站强大的计算功能,协调导弹之间的目标分配与攻击。同时,通过与其它火力单元的数据在制导站中的融合处理,数据链中可以加入不同类型的导弹攻击信息,便于实现从武器系统发现目标直到对目标拦截全过程的联网制导,解决了目前导弹在发射后,制导飞行阶段,脱离网络,单独攻击目标的问题,实现了协同攻击。

2 协同攻击的目标分配

现在研究采用上述方案对不同类型的防空作战单元的多弹协同攻击目标的目标分配问题。

目标分配的准则很多,基于使目标总期望生存概率最小是最常用的目标分配原则。在此假设为了对付敌方的饱和攻击,不同防空导弹作战单元采用齐射方式发射了J种类型的防空导弹,通过基于制导站中继的方式实现不同类型导弹间的数据交换,实现协同拦截K个来袭目标。其中第k个目标的威胁度为ωk,第i种类型的导弹对第k个目标的杀伤概率为pik。经过制导站对协同拦截过程的分析,分配给第k个目标的武器数为xik≥0,则第k个目标的生存概率为:

(1)

因此,所有目标的总期望生存概率可表示为:

(2)

目标分配问题的求解是确定分配给各目标的导弹类型及数量,使得所有来袭目标的总期望生存概率最小。

(3)

式中：X是由xjk,j=1,2,…,J,k=1,2,…,K构成的矩阵。

此外,由于分配给不同目标的武器数不是无限的,且导弹的类型及其可分配的武器数也不是无限的,因此,需要增加约束条件,使得目标分配问题表示为约束最优化问题:

(4)

(5)

式中:Vk为分配给第k个目标的最大武器数目;Uj为给第j种类型导弹可分配的最大武器数目。

3 基于萤火虫群优化算法的目标分配实现

对上述问题的实现就演化成式(3)中自变量为xik时,在式(4)和式(5)约束条件下的求最优解问题。

萤火虫群优化(glowworm swarm opimization,GSO)算法是印度学者Krishnanad和Ghose在2005年提出的一种新型智能群优化算法[2-3],在求解多模态函数极值问题上取得了较好的效果,因其运算速度快、容易实现而受到很多学者们的青睐,被应用到许多领域。而且由于萤火虫的聚集及算法过程非常类似于导弹间的协同,因此,采用萤火虫算法来求解上述问题。

在萤火虫算法中,设萤火虫i的绝对亮度比萤火虫j的亮度大,则萤火虫j被萤火虫i吸引而向i移动。萤火虫i对萤火虫j的吸引力为:

(6)

式中:β0是当两个萤火虫之间距离r=0时的吸引力;γ为光吸收系数;rij为萤火虫i和j之间的距离,即:

(7)

由于萤火虫j被萤火虫i吸引而向萤火虫i移动,则萤火虫j的位置更新公式为:

Xj(t+1)=Xj(t)+βij[Xi(t)-Xj(t)]+αεj

(8)

式中:t为迭代次数;Xi和Xj分别为萤火虫i和j所处的空间位置;βij为萤火虫i对萤火虫j的相对吸引力;α为常数,一般可以取[0,1]内的数;εj是由均匀分布得到的随机数向量。

上述算法中的α虽然可以随意在[0,1]取值,它实际上反映了计算迭代中的步长,它需要在计算精度、计算速度和陷入局部最优解之间寻找平衡。在种群搜索过程中,α越大,越容易更快搜索到全局最优值,但往往降低了搜索精度,有时结果有发散现象;α越小,种群搜索速度就会降低,解的精度却会提高,但又容易陷入局部最优。因此,种群搜索过程中应根据不同阶段的搜索结果,采用动态调整α值的方法。

为此,引入荧光因子:

(9)

式中:xmax表示当时荧光素值最大的萤火虫的位置;dmax取种群中所有萤火虫与亮度值最大萤火虫之间的距离值。

将α更新为基于荧光因子的自适应动态值:

αi=αmin+(αmax-αmin)Hi

(10)

式中：αmin和αmax分别为α的最小值和最大值。通过限制α值的范围,可以避免萤火虫过于分散,这时可根据式(9)和式(10)对移动步长作动态调整,这样的自适应步长能够根据荧光因子自动调整,提高了搜索速度,避免了结果发散。

4 验证与分析

求解时,首先进行初始化。设初始的α=0.1;初始吸引力β0=0.2;吸收系数γ=1;仿真迭代次数N=200。

在计算导弹间协同目标分配时,只能是要么对一个目标分配导弹,要么不分配,为此需要确定分配准则。在此,以防空导弹常规作战中的实际情况取值,由于目标是否被分配只有0,1两种情况,取杀伤概率以0.8为准则对函数值进行离散化,0表示不分配,1表示分配。

选取rand(n,m)矩阵作为xik的取值:

(11)

式中：n和m表示为对第m号目标用第n个导弹进行攻击。

假设由4种不同类型的防空导弹武器系统用来拦截8个来袭目标,4种武器系统中可用的导弹数分别为{3,1,2,2},每个目标最多可分配1个武器,作为约束条件。武器系统及导弹间协同拦截。那么J=4;K=8,取仿真步长为0.01 s。设定的各目标的威胁度和以及对各目标的单发杀伤概率如表1所示。

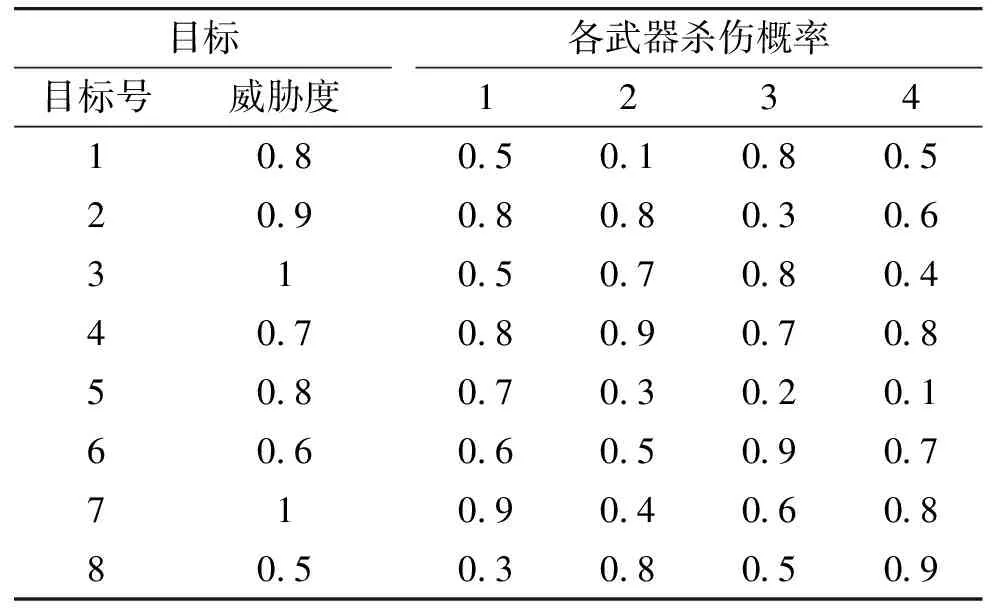
表1 不同类型武器杀伤概率及目标威胁度

两种算法的结果是相同的。表2给出了经过仿真计算的最优武器目标分配方案。

目标类型1的武器拦截目标2、目标5和目标7;火力平台2的武器拦截目标4;目标类型3的武器拦截目标1和目标3;目标类型4的武器拦截目标6和目标8。

图1和图2分别给出了采用GSO和具有自适应步长的GSO算法的算法收敛情况。

表2 最优武器目标分配方案

GSO算法和自适应步长GSO算法平均迭代次数分别为105和63,说明后者具有快速性上的明显优势。自适应步长GSO算法最大迭代次数为190,最大解算结果耗时1.9 s,如果采用VC语言实现,耗时可在控制在1.0 s以内,可以满足防空作战对快速性和实时性的作战要求。验证了实现方案和算法的有效性。

参考文献:

[1] 沈川. 基于弹载数据链的信号检测技术研究 [D]. 沈阳: 沈阳理工大学, 2013.

[2] 欧阳喆, 周永权. 自适应步长萤火虫优化算法 [J]. 计算机应用, 2011, 31(7): 1804-1807.

[3] 黄正新, 周永权. 自适应步长萤火虫群多模态函数优化算法 [J]. 计算机科学, 2011, 38(7): 220-224.

[4] 刘传波. 基于Memetic算法的动态武器目标分配问题研究 [J]. 舰船电子与工程, 2012: 32(10)34-37.

[5] XIN Bin, CHEN Jie. An estimation of distribution algorithm with efficient constructive repair/improvement operator for the dynamic weapon-target assignment[C]// IEEE. Proceedings of the 31st Chinese Control Conference. [S.l.]: IEEE, 2012: 2346-2351.

[6] 吴胜亮. 众多导弹协同作战制导控制的研究 [D]. 南京: 南京航空航天大学, 2013.