一种利用遥测数据重构外测级间段轨迹的方法
2017-05-03王召刚栾瑞鹏孟庆海
王召刚, 栾瑞鹏, 孟庆海
(91550部队, 辽宁大连 116000)
0 引言
在航天器飞行级间段,由于火焰、震动等原因,外测设备跟踪丢失或测元精度很低[1]。导致全局样条模型的外测轨迹融合解算[2-3]结果在级间段与遥测加速度测量结果的偏差超出遥外测精度范围。
为给出与外测全程解算精度相一致的完整级间段轨迹,考虑综合利用遥外测量数据。遥测加速度计在级间段可以给出符合航天器运动特性的、质量较高的连续测量结果。文中以级间段前某时刻高精度外测融合解算结果为起始值,利用遥测视加速度测量结果建立方程,计算级间段轨迹。这种方法通过选择外测结果为起始值消除了级间段前遥测加速度测量的累积误差影响。为了减小级间段过程中新增加遥测加速度测量误差影响,建立了误差修正模型,模型中假设发射原点误差影响已消除,只考虑视加速度误差源的3个部分,平台调平误差、瞄准误差和加速度计测量误差,然后建立了关于误差修正模型参数的寻优模型。修正遥测加速度的测量误差后,递推轨迹和非级间段外测轨迹、递推轨迹反算测量元和级间段可用测量元的比较结果能够符合外测测量精度。
1 轨迹递推计算模型
高B0、L0、H0、A0分别为发射原点的大地纬度、经度、高程和方位角,对应地心系坐标为Xof。地心系到法线发射系的坐标变换矩阵为[4]:
(1)
式中Rx、Ry、Rz分别为绕x轴、y轴、z轴正向旋转矩阵。
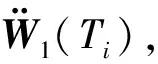
1.1 前推地心惯性坐标系下的轨迹参数
记地球自转角速度为ω,下式把地心系外测位置、速度参数转到地心惯性系下:
(2)
下式把发射惯性系下视加速度参数转到地心惯性系下:
(3)
地心惯性系下轨迹递推模型如下:
(4)
式中i=J,…,Q,令目标到地心的距离为:
r(Ti)=(Xy2(Ti)TXy2(Ti))1/2
(5)
引力加速度Xy2(Ti)采用下式计算:
(6)
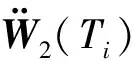
1.2 递推初始点的选择及递推结果评估
在级间段前加速度平稳的段落选择外测精度较高的点作为初始点。轨迹精度评估采用下面方法[5]:
Step1 在参加轨迹估计的Ti时刻的测量元集合Cr上添加误差得到C0。
Step2 根据C0,利用最小二乘交汇算法求解航天器位置P(Ti)、速度V(Ti)。
Step3 计算位置偏差和速度偏差:
DP(Ti)=((P(Ti)-X3(Ti))(P(Ti)-X3(Ti))T)1/2
Step4 重复上面三步N次,统计Ti时刻位置和速度偏差的均方根差。
其中,测元误差根据设备测量精度添加。级间段后的重构轨迹与外测结果的偏差越小越好,偏差小于均方根误差3倍,重构轨迹满足外测精度指标。
2 视加速度误差源及影响消除方法
考虑视加速度3个误差源:瞄准误差、平台调平误差和加速度计误差。前两项表示惯性平台坐标系(OX0Y0Z0)与发射惯性系(OX1Y1Z1)的不重合。
2.1 视加速度误差建模
瞄准误差为惯性平台系[4]OX0轴所指大地方位角与装订射向A0不一致引起的视加速度参数偏差。
加速度计测量误差采用文献[4]中的模型:
(7)
式中,C0、C1、C2为模型待求系数,模型意义参见文献[4]。
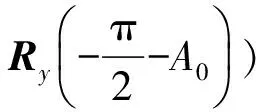
在由地心系到惯性平台系的坐标变换中,先转射向后调平,这样调平修正不会对射向旋转产生影响。令:
(8)
V=Rx(ξ1)Rz(η1)
(9)
由地心系到惯性平台坐标系的坐标变换矩阵为:
Cz=VC
(10)
2.2 视加速度误差模型系数求解
令视加速度误差模型的参数向量为:
β=[C0x,C1x,C2x,C0y,C1y,C2y,C0z,C1z,C2z,ξ0,η0,A0]
以TJ时刻外测参数为初始值,遥测视加速度参数为已知值,TJ之后的轨迹参数可以表示为β的函数:
(11)
选择级间段结束后的(TL,TM)之间外测轨迹参数作为Fi(β)的逼近目标,建立优化模型求解β:
(12)
β搜索范围[β0-Δβ,β0+Δβ]通过经验设置。由于平台调平误差、瞄准误差与加速度计测量误差之间存在耦合性,模型(12)中β的解不唯一。这里采用遗传算法求解模型。
3 算例及分析
假设航天器飞行12 s左右进行级间段分离。这个时间段没有光学测量,只有雷达测量,主动式雷达与应答机失联,被动式雷达测元不足且精度不高,全局样条表示模型的融合解算轨迹精度变差。级间段附近轨迹解算精度评估结果如图2所示,横坐标为时间t,纵坐标为位置偏差P和速度偏差V的均方根差,间断部分为测元不足导致速度和位置的均方根量级超过104。选择级间段前加速度变化平稳、精度可靠的99 s作为轨迹递推模型起始点。选择加速度变化平稳、精度变化平稳的11~115 s的外测融合解算轨迹作为递推模型逼近对象。
利用遗传算法求解优化模型(12),利用优化后的误差修正模型对遥测视加速度误差进行误差修正。视加速度测量误差修正前与修正后递推计算轨迹和外测融合解算轨迹的比较结果如图3所示,图3(a)为位置P,图3(b)为速度V,级间段后110~115 s的外测融合解算轨迹是优化逼近目标,误差修正前后的位置偏差达到20 m多;误差修正使得递推计算轨迹与外测融合解算的偏差变小,级间段后110~115 s之间的重构轨迹和外测轨迹的位置和速度偏差的均方根分别为1.24 m和0.52 m/s,满足外测样条融合结果精度要求。
重构轨迹与遥测、外测融合解算的合加速度A比较结果如图4所示,图4(a)是合加速度,图4(b)是遥测测量轨迹和重构轨迹合加速度的比较结果。图4(a)显示,遥测加速度与外测融合解算加速度在级间段具有较大的不一致趋势项,在级间段之后趋势一致,这与级间段内外测跟踪异常,级间段后外测跟踪恢复的情况相一致。遥测加速度与重构轨迹加速度在级间段一致性较好,说明重构轨迹很好的弥补了外测样条融合解算的不足,使得级间段遥外加速度误差与全程误差量级相一致,变化趋势一致;图4(b)显示重构轨迹和遥测轨迹的合加速度比较结果呈现斜率为0.032 96线性变化,这是对加速度测量误差修正的结果。
由于调平误差和加速度计测量误差之间存在耦合性,β的解不唯一,各分量在遗传进程中没有趋势性的进化规律。为了在遗传算法中考察β解的唯一性,进行了1 500代进化。如图5所示为最后250次进化中平台调平误差子午量ξ0和加速度常值误差项C0x的变化趋势。进化中轨迹偏差的平均值已稳定,变化不超过2.327 5e-004 m,而对应的解向量分量在搜索区间内呈随机性变化(其他各个参数也是呈随机性变化),这说明β解不唯一。
4 结束语
利用全程样条模型融合解算获得级间段轨迹的方法实际是一种轨迹内插方法。与一般基于常值、多项式等模型的内插方法不同,文中利用遥测加速度、级间段前某一时刻融合解算轨迹参数和加速度误差修正模型建立了求解级间段轨迹的冗余模型,利用优化方法求解冗余模型参数,进而求得级间段轨迹。这种方法得到的级间段轨迹与外测全程精度相一致。
参考文献::
[1] 刘利生, 吴斌, 吴正容, 等. 外弹道测量精度分析与评定 [M]. 北京: 国防工业出版社, 2010: 98-99.
[2] 张艳, 石晟玮, 郭军海, 等. 基于样条约束的弹道融合抗差估计方法 [J]. 弹道学报, 2011, 23(1): 40-44.
[3] 李东, 孙杰. 弹道跟踪数据融合处理的快速算法 [J]. 飞行器测控学报, 2015, 34(4): 368-373.
[4] 王正明. 弹道跟踪数据的校准与评估 [M]. 长沙: 国防科技大学出版社, 1999: 168-169.
[5] 王召刚, 谢玉珍. 遗传算法的外弹道参数绝对误差界确定方法 [J]. 导弹试验技术, 2014, 112(4): 54-56.
