基于系统标定理论的斜置光学惯导标定算法研究

刘群昌, 唐梦丽, 董金华, 牟方佳, 杨道安

(中国航天科工集团第九总体设计部, 武汉 430040)

0 引言

光学惯导的敏感元件采用斜置安装技术,可以扩大载体三轴方向的角速度和加速度测量范围,节省传感器安装空间,这种斜置安装方式给惯导标定带来了新的技术难题。文献[1]利用惯导与台体的方向余弦矩阵,采取传统的元件级标定方法,完成惯导单元标定,标定精度不仅取决于台体定位精度,而且受惯导与台体的方向余弦矩阵精度影响;文献[2]将传统的零位、比例因子、安装误差等参数等效考虑为一个转换矩阵,采用元件级标定技术分离误差参数,标定的最终精度依赖于台体的定位精度。

文中提出了基于系统标定理论[3]的斜置光学惯导标定技术,通过建立虚拟的台体坐标系,采用自对准技术获取台体坐标系与光学惯导的姿态关系,将斜置光学惯导的输出转换到虚拟台体坐标系中,完成在台体坐标系中的系统标定,利用虚拟台体坐标系与惯导坐标系之间的误差参数转换关系,将台体坐标系中标定的误差参数转换到惯导坐标系中,完成光学惯导的误差参数标定。采用该算法对斜置惯导进行标定,能自主测量台体坐标系与惯导坐标系之间的方向余弦矩阵,且对台体的定位精度要求不高,惯导误差参数辨识精度高,对工程应用具有重要的参考意义。

1 惯导误差模型

对光学惯导固定参考轴作如下假设:x轴与Ax加速度计输入轴一致(Maxy=Maxz=0),y轴位于Ax、Ay加速度计轴构成的平面内(Mayz=0),则光学惯导系统中惯性仪表的误差模型可表述为:

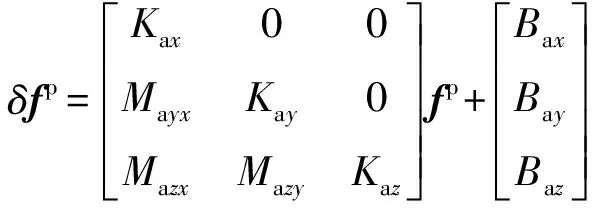
2 斜置系统标定原理

IMU采用斜置安装技术,坐标轴由3个正交陀螺、加速度计敏感轴线约束,安装误差依然为小量,坐标关系示意图如图1所示。

2.1 粗对准

通过加速度计信息可以获取俯仰角和滚动角的值,方位的辨识方法参见第2.3节,利用得到的方位角、俯仰角和滚动角信息再重新计算姿态信息Cgp,完成初始位置静基座对准。

2.2 误差分离

对b系下的误差模型定义与p系一致,即δfb

通过文献[4]可知,系统标定方法可以分离b系下的21个误差参数。

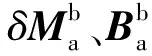
从上式可以看出误差参数转换到p系后为24个,根据p系下定义的误差模型可知,需要对安装误差做进一步的合并处理,限于篇幅在此不再推导。

2.3 方位辨识

3 仿真结果与结论

根据推导出的斜置光学惯导系统标定方法,对惯导在各个不同典型的初始条件进行了仿真,仿真初始条件:

1)台体:方位角90°,俯仰角0°,横滚角90°,惯导:方位角93°,俯仰角50°,横滚角50°;

2)台体:方位角93°,俯仰角3°,横滚角93°,惯导:方位角87°,俯仰角70°,横滚角70°。

仿真结果部分参数如表1。

仿真结果表明,利用光学惯导斜置系统标定算法计算出的惯性仪表参数与理论值的差值在1.0e-6数量级,陀螺零位误差在1.0e-3数量级,参数收敛速度较快,能自主测量惯导坐标系到台体坐标系的坐标转换,且降低了对转台的定位精度的要求,对实际工程应用具用重要的参考意义。

表1 仿真结果

参考文献:

[1] 程耀强, 徐德民, 万彦辉, 等. 斜装激光陀螺石英加速度计标定算法研究 [J]. 压电与声光, 2013, 35(3): 362-367.

[2] 郭鹏飞, 任章. 斜置惯性测量单元的一体化标定技术 [J]. 中国惯性技术学报, 2007, 15(3): 377-381.

[3] 董金华, 杨道安, 陆俊清, 等. 基于系统标定理论的机械和光学惯导统一标定算法 [J]. 弹箭与制导学报, 2014, 34(3): 29-32.

[4] 杨晓霞, 黄一. 激光捷联惯导系统的一种系统级标定方法 [J]. 中国惯性技术学报, 2008, 16(1): 1-7.