基于强跟踪SDRE滤波的GPS/INS组合导航

任珊珊, 赵良玉,2, 娄泰山

(1 北京理工大学宇航学院, 北京 100081; 2 飞行器动力学与控制教育部重点实验室, 北京 100081;3 郑州轻工业学院电气信息工程学院, 郑州 450002)

0 引言

GPS/INS组合导航系统已被广泛应用于航空、航天、航海、兵器、勘探等诸多领域,其通过对GPS和INS的数据进行信息融合,实现优势互补,提高载体的导航定位精度。GPS/INS组合导航采用直接法对导航参数进行估计时,虽能准确反映载体真实状态的演变情况,但其系统状态方程的非线性给设计导航滤波方法带来了一定的困难。

针对GPS/INS组合导航系统直接法的非线性状态方程,通常采用扩展卡尔曼滤波(extended Kalman filtering,EKF)方法对导航状态进行估计。然而,该方法对系统线性化所带来的截断误差极大地影响了导航滤波的精度,同时计算Jacobian矩阵增加了系统复杂度,不利于状态的实时估计。为了解决这些问题,状态相关黎卡提方程滤波方法应运而生[1]。SDRE滤波是一种基于状态相关因子(state-dependent coefficients,SDC)的滤波方法,该方法通过对非线性状态方程进行分解和求解黎卡提方程来估计系统的状态,从而避免了状态方程的线性化和Jacobian矩阵的计算[2-3]。Nemra将SDRE滤波应用于无人机的GPS/INS组合导航,整体表现较EKF更好[4]。自主编队飞行的空间飞行器进行相对导航时采用SDRE滤波,同样取得了较好的导航性能[5]。

上述研究均假设导航系统模型精确已知、噪声统计特性已知,但实际应用中,导航系统可能会受到未知输入和不确定噪声的影响。为了解决此类问题,学者们提出了H∞滤波[6],强跟踪滤波(strong tracking filtering,STF)[7]等方法来处理导航系统面临的不确定性。

文中针对用于飞行器状态估计的GPS/INS组合导航系统,提出了一种鲁棒的直接组合导航滤波方法,能有效克服导航系统的不确定性,增强导航系统的鲁棒性,提高飞行器状态快速变化时的跟踪能力。

1 GPS/INS组合导航非线性状态方程

文中采用直接法对导航系统参数进行估计,导航坐标系选取为东北天(east-north-up)坐标系,考虑陀螺仪和加速度计的常值漂移,则该组合导航系统的状态方程为:

(1)

x=[φe,φn,φu,ve,vn,vu,φ,λ,h,εe,εn,εu,Δe,Δn,Δu]T

(2)

式中:状态量φe、φn、φu为数学平台误差角;ve、vn、vu为载体的东向、北向、天向的速度;φ、λ、h为载体所在的纬度、经度和高度;εe、εn、εu为陀螺仪常值漂移;Δe、Δn、Δu为加速度计常值漂移。噪声量w=[ωεe,ωεn,ωεu,ωΔe,ωΔn,ωΔu]T由陀螺仪和加速度计的随机误差组成。

系统状态x的非线性函数f(x,w)可进一步展开为:

(3)

其中δve、δvn、δφ、δh、fe、fn、fu分别是INS和GPS在东向和北向的速度差、纬度差、高度差以及加速度计测量值在东、北、天3个方向的分量。

系统的量测方程为:

z=h(x)+v

(4)

式中:量测信息z=[vge,vgn,vgu,pge,pgn,pgu]T为GPS测得的载体速度和位置;v为量测噪声。

v=[vvge,vvgn,vvgu,vpge,vpgn,vpgu]T

(5)

式中：vvge、vvgn和vvgu分别为GPS速度观测值在导航坐标系3个方向的随机误差;vpge、vpgn和vpgu分别为GPS位置观测值在导航坐标系3个方向的随机误差。

2 强跟踪SDRE滤波算法

2.1 算法流程

SDRE滤波算法先采用SDC分解的方法将非线性系统分解成状态和转移矩阵的形式,然后对黎卡提方程进行求解得到每一步的协方差阵,再利用卡尔曼滤波更新状态的估计。通常情况下,SDRE滤波所采用的黎卡提方程可分为两种:状态相关代数黎卡提方程(state-dependent algebraic Riccati equation,SDARE)和状态相关微分黎卡提方程(state-dependent differential Riccati equation,SDDRE)。SDARE在滤波每一步中需要计算当前时刻的协方差,计算量大[9],而SDDRE在离散系统中的更新方法和卡尔曼滤波并无二致,故文中采用了SDDRE滤波。

以式(1)和式(4)组成的非线性系统为例,用SDC思想将其分解可得:

(6)

式中f(x)=F(x)x,h(x)=H(x)x。

离散化式(6),并引入自适应渐消因子λk,得到强跟踪SDRE滤波过程:

(7)

(8)

式中:Δt是滤波时间间隔;Φk+1/k是离散化之后的转移矩阵;Pk是k时刻状态的协方差矩阵;Qk是系统噪声wk的方差。

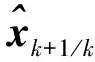
式中:Rk+1是量测噪声vk+1的方差;Θk+1是离散化之后的量测矩阵。

基于式(8)中渐消因子的求解,文中提出了强跟踪SDRE滤波算法,其算法流程如图1所示。

2.2 自适应渐消因子的确定

强跟踪滤波基于残差正交化原理[10]:

(12)

由于自适应渐消因子λk的引入,欲使式(12)成立,即使下式成立[11]:

(13)

将式(9)代入式(13)得到:

(14)

再将式(8)代入式(14)得到:

(15)

令:

(16)

(17)

则有:

(18)

(19)

式(16)中的残差序列Vk可由下式求得:

(20)

其中0<ρ≤1是遗忘因子,通常取0.95。

3 组合导航仿真验证

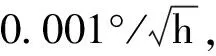
为了验证强跟踪SDRE滤波对模型不确定性的鲁棒性,假设现有模型是精确模型,保持滤波模型不变,飞行数据中引入未知输入:

(21)

使真实模型为:

xk+1=f(xk,uk)+Δx

(22)

分别采用SDRE滤波和强跟踪SDRE滤波对其进行仿真。图4为SDRE滤波和强跟踪SDRE滤波对位置的滤波值与真实位置之差,图5为速度的滤波值和真实速度之差。由图4可以看出,在500～800 s的时间段内,采用强跟踪SDRE滤波的位置误差保持在5 m之内,明显优于SDRE滤波,滤波结果更接近于真实状态。在平稳飞行时间内,采用强跟踪SDRE滤波后,速度误差小于1 m/s,位置误差小于5 m。特别地,从图5可以看出,强跟踪SDRE滤波对状态的突变跟踪能力相对于SDRE滤波更强,在状态突变时刻,误差相对于SDRE滤波更小。仿真结果表明,强跟踪SDRE滤波能够较好的跟踪状态的变化,抑制了模型不精确带来的干扰,其导航性能优于SDRE滤波。

4 结论

文中将自适应渐消因子引入SDRE滤波,提出了一种强跟踪SDRE滤波算法,并将其用于飞行器的GPS/INS组合导航系统中进行数据融合及状态估计。强跟踪SDRE滤波算法通过求解状态相关分解后的黎卡提方程,有效地克服了系统模型的不确定性,避免了非线性系统线性化时面临的截断误差及计算Jacobian矩阵的问题。通过GPS/INS组合导航系统仿真算例对比,在模型存在不确定性及飞行状态突变情况下,强跟踪SDRE滤波方法的滤波效果明显优于SDRE滤波,有助于得到更为准确的状态估计。

参考文献:

[1] MRACKEK C P, CLONTIER J R, D’SOUZA C A. A new technique for nonlinear estimation [C]∥IEEE. Proceedings of the 1996 IEEE International Conference on Control Applications. Piscataway.[S.l.]: IEEE, 1996: 338-343.

[2] ÇIMEN T. Survey of state-dependent riccati equation in nonlinear optimal feedback control synthesis [J]. Journal

of Guidance, Control, and Dynamics, 2012, 35(4): 1025-1047.

[3] STRANO S, TERZO M. Accurate state estimation for a hydraulic actuator via a SDRE nonlinear filter [J]. Mechanical Systems & Signal Processing, 2016, 75(15): 576-588.

[4] NEMRA A, AOUF N. Robust INS/GPS sensor fusion for UAV localization using SDRE nonlinear filtering [J]. IEEE Sensors Journal, 2010, 10(4): 789-798.

[5] PARK H E, KIM Y R. Relative navigation for autonomous formation flying satellites using the state-dependent riccati equation filter [J]. Advances in Space Research, 2016, 57: 166-182.

[6] NAGPAL K M, KHARGONEKAR P P. Filtering and smoothing in an H∞setting [J]. IEEE Transactions on Automatic Control, 1991, 36(2): 152-166.

[7] 周东华, 席裕庚, 张钟俊. 非线性系统带次优渐消因子的扩展卡尔曼滤波 [J]. 控制与决策, 1990(5): 1-6.

[8] BEIKZADEH H, TAGHIRAD H D. Robust SDRE filter design for nonlinear uncertain systems with an H∞performance criterion [J]. ISA Transactions, 2012, 51(1): 146-152.

[9] JAGANATH C, RIDLEY A, BERNSTEIN D S. A SDRE-based asymptotic observer for nonlinear discrete-time systems [C]∥ IEEE. Proceedings of the 2005 American Control Conference. Portland: IEEE, 2005: 3630-3635.

[10] 付梦印, 邓志红, 闫莉萍. Kalman滤波理论及其在导航系统中的应用 [M]. 2版. 北京: 科学出版社, 2010: 101.

[11] 郭泽, 缪玲娟, 赵洪松. 一种改进的强跟踪UKF算法及其在SINS大方位失准角初始对准中的应用 [J]. 航空学报, 2014, 35(1): 203-214.