采用矩阵填充的稀疏阵列MIMO雷达成像方法

赵小茹, 童宁宁, 丁姗姗, 朱 烨

(1 空军工程大学防空反导学院, 西安 710051; 2 中国电信股份有限公司西安分公司, 西安 710051)

0 引言

MIMO雷达利用自身多发多收的结构特点得到远多于实际阵元的虚拟阵列,能够将实孔径雷达(RAR)和逆合成孔径雷达(ISAR)的各自特点相结合,以空间采样代替时间采样,实现单快拍成像。文献[1]提出MIMO雷达单次快拍成像算法,但所需阵元数目仍然较多,系统复杂度高。在此基础上,为降低阵列规模,文献[2]研究了稀疏阵列成像技术中存在的数据缺失等问题。针对稀疏阵列成像,有学者提出将压缩感知(CS)理论应用于MIMO雷达[3-4],对稀疏回波数据的压缩重建,克服稀疏阵列的缺陷,实现单快拍成像,但在使用CS进行稀疏重构时,稀疏变换矩阵的选取得当与否对稀疏重构的精确度和成像质量的好坏有重要影响。

继压缩感知之后,学者Candes等在2008年提出矩阵填充原理[5-7],旨在通过稀疏低秩矩阵中的少量已知元素重构得到完整的数据矩阵。MC理论指出,若待估计矩阵具有低秩性,则说明可以在低维空间中获得该未知矩阵的特征值,再基于低秩约束最优化问题建立已知元素和未知元素之间的联系,最后通过填充重构得到完整矩阵。目前,已有学者将MC原理应用到雷达信号处理领域[8],进行如MIMO雷达目标参数估计[9-10]、欠采样情况下SAR成像[11]等研究,对比MIMO雷达成像算法,因为信号模型建立的差异性,目前针对MIMO-MC单次快拍成像方法的研究还很少。文中针对稀疏阵列,采用MC理论,提出一种稀疏阵列MIMO雷达单快拍成像方法,能够在减少所需阵元数的同时有效避免成像质量的损失,精确的完成矩阵的填充重构。

1 矩阵填充的基本理论[12]

矩阵填充属于稀疏约束下的反问题,当待估计矩阵满足低秩或近似低秩的稀疏先验特性时,可由少量已知元素填充重构出原矩阵。假设一个待恢复矩阵Mn×m,其中{Mij,(i,j)∈Ω}是k个已知元素的集合,Ω是势k的均匀随机采样集,通过设定约束条件,满足未知矩阵与低秩矩阵之间特定的映射关系,完成矩阵填充。

解决矩阵填充问题最初的优化方法是一个NP-hard问题,可以利用凸优化理论将其转化为一个能够重构成半正定规划的凸优化问题:

minimize ‖X‖*

subject toPΩ(Xij)=PΩ(Mij),(i,j)∈Ω

(1)

2 基于MC理论的MIMO雷达成像方法

2.1 稀疏天线布阵方式

根据等效相位中心定理[12](phase center approximation,PCA),M发N收的均匀线阵可以等效为具有M·N个收发同置阵元的虚拟阵列,大幅度增加了阵元数,但实现MIMO雷达单次快拍成像所需的阵元数目仍然较多。基于文献[3]提出的稀疏阵列,假设原始均匀线阵由N个间距为d的接收阵元和M个间距为N·d的发射阵元组成,固定接收阵列首尾两端阵元位置,保证成像分辨率不变,从剩余的(N-2)个阵元中随机抽取(N′-2)个阵元,等效得到含M·N′个收发同置阵元的稀疏阵列,定义稀疏度为Γ=(N-N′)/N。以4发7收的MIMO雷达为例说明稀疏阵列布阵方式,如图1所示。

其中,图1(a)表示实际稀疏阵列,图1(b)为经过PCA等效后得到收发同置的稀疏虚拟阵列,阵列孔径总长度保持不变,阵元减少。

2.2 雷达成像方法

采用混沌相位编码信号作为M发N收MIMO雷达的发射信号,以提供M路相互正交的信号,第m路发射信号表示为:

sm(t)=exp(jφm(t))exp(j2πf0t)

m=1,2,…,M

(2)

式中:f0为载频;φm(t)为相位编码函数。发射信号满足:

m2=1,2,3,…,M

(3)

其中g(t)为相位编码信号的相关函数。

Dmq+Dqn=2Diq+ΔDq≈

(4)

式中ΔDq为等效产生的距离偏差。进行相干检波和匹配滤波后,第n个接收阵元收到的回波信号表示为:

i=1,2,…,M·N

(5)

(6)

观察式(6),当阵元缺失时,方位向上该单元没有回波信号,故无法直接通过IFFT变换实现成像。而对于随机稀疏阵列,由于阵元的缺失,会造成某个方位向上全距离单元回波信号的缺失,导致回波数据矩阵出现全零列,无法应用MC完成矩阵填充。对此,文中提出针对单观测向量的联合处理方法,通过特定的数据处理过程实现MC原理在稀疏阵列MIMO雷达成像的有效应用,避免信号缺失导致矩阵填充失效的问题。

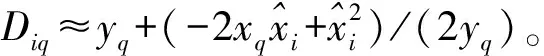
i=1,2,…,M·N′

(7)

i=1,2,…,M·N′

(8)

(9)

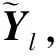
(10)

式中:Ω与式(6)中的Ω相对应为随机稀疏阵列对应的随机采样集。目前,通过拉格朗日乘子类型的算法如SVT算法、IALM算法等、贪婪追踪算法等一系列算法[12]可以解决式(10)所示的凸优化问题。

考虑远场条件下多散射点的情况,在进行方位向压缩后得到在单个距离单元内的多散射点回波信号为:

i=1,2,…,M·N′

(11)

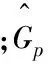
为更清晰的说明文中提出成像方法的实现思路,将方法实现的流程图整理为如图2所示。

MIMO雷达回波数据经过数据处理后,对每个距离单元进行MC处理,估计得到未知元素将稀疏矩阵填充重构,进而得到MIMO雷达在单快拍下所有距离单元内的散射点分布,即运动目标的二维图像。

3 仿真实验

为验证文中所提方法有效性,仿真稀疏阵列MIMO雷达成像场景。参照图1从6发100收的均匀线阵(d=1 m)的接收阵列中随机抽取50个阵元,得到6发50收的稀疏阵列(Γ=50%)。图3所示仿真目标由11个散射点组成,与阵列相距10 km。发射信号为一组含4个40码元的四相编码正交信号,载频为10 GHz,子脉冲时宽为2 ns。

稀疏度Γ=50%时,分别采用直接IFFT和MIMO-MC两种方法实现的目标二维图像如图4所示,其中图4(a)为未稀疏原始均匀线阵的二维图像,图4(b)是采用IFFT方法的二维成像结果,图4(c)是采用MIMO-MC方法的二维成像结果。

观察发现,MIMO-MC方法得到的图4(c)与图4(a)相近,能够较为精确的恢复目标散射点模型,且图4(c)的估计精度与图4(a)基本一致,但图4(b)的图像中出现了虚假的散射点。仿真结果表明,文中所提的MIMO-MC方法能够实现MIMO雷达的稀疏成像。

为检验文中所提方法的估计精度和填充恢复性能,仿真给出图4所圈点的一维方位图像如图5所示,其中红色圈点代表所提方法,蓝色细线代表Γ=50%时直接进行IFFT变化的方法,黑色细线代表未稀疏均匀线阵下直接进行IFFT变化得到的结果。

观察图5可以看出,文中所提方法得到的曲线与未稀疏均匀线阵所得曲线近似一致,仅有少量旁瓣且明显低于直接用IFFT方法得到的曲线。仿真结果证明,MIMO-MC方法能够较为精确的实现对目标图像的稀疏重构且估计精度高。

进一步利用均方误差指标计算(mean square error,MSE)公式,在不同稀疏度时,对稀疏阵列下的成像效果进行评估。

(12)

式中:S1代表均匀满阵得到的回波信号;S2为阵列稀疏后不同方法处理得到的回波信号。当稀疏度Γ以10%为间隔从20%变化到80%时,重复进行100次蒙特卡洛实验,统计得到计算IFFT方法和MIMO-MC方法成像结果的均方误差曲线如图6所示。

由图6看出,两种成像方法的标准偏差均随着稀疏度增加而升高,并且MIMO-MC方法的标准偏差始终低于IFFT方法。仿真结果证明,文中所提方法在不同的稀疏度下均可以较为精确的实现稀疏MIMO雷达阵列的二维成像。

4 总结

文中提出了一种MIMO-MC成像方法,采用MC理论估计未知元素以实现目标图像的精确重构。仿真检验了该方法对目标所成的一维方位图像和二维图像,采用成像结果标准偏差量化分析,并检验了不同稀疏度对成像效果的影响。结果表明,采用文中提出的MIMO-MC方法的成像效果与未稀疏均匀线阵基本一致,并对稀疏度具有适应性,从而证明了所提算法的有效性。

参考文献:

[1] 王怀军, 粟毅, 黄春琳. 基于天线布阵的MIMO雷达成像研究 [J]. 信号处理, 2009, 25(8): 1203-1208.

[2] 陈刚. 稀布阵列MIMO雷达成像技术研究 [D]. 南京: 南京理工大学, 2014.

[3] 顾福飞, 池龙, 张群, 等. 基于压缩感知的稀疏阵列MIMO雷达成像方法 [J]. 电子与信息学报, 2011, 33(10): 2452-2457.

[4] 赵小茹, 童宁宁, 胡晓伟, 等. 二维CZT的稀疏阵列MIMO雷达快速成像算法 [J]. 空军工程大学学报, 2017, 2(18): 60-65.

[5] CANDES E J, RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717-772.

[6] CANDES E J, TAO T. The power of convex relaxation: near-optimal matrix completion[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2053-2080.

[7] CANDES E J, PLAN Y. Matrix completion with noise[J]. Proceedings of the IEEE, 2010, 98(6): 925-936.

[8] 赵玉娟, 郑宝玉, 陈守宁. 矩阵填充及其在信号处理中的应用 [J]. 信号处理, 2015, 31(4): 423-436.

[9] SUN S, BAJWA W U, PETROPULU A P. MIMO-MC radar: a MIMO radar approach based on matrix completion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 1839-1852.

[10] CHI Y. Sparse MIMO radar via structured matrix completion [C]// IEEE. 2013 IEEE Global Conference on Signal and Information Processing.[S.l.]:IEEE, 2013: 321-324.

[11] YANG D, LIAO G, ZHU S, et al. SAR imaging with undersampled data via matrix completion[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(9): 1539-1543.

[12] 马晓慧. 矩阵填充理论方法分析 [D]. 杭州: 浙江大学, 2012.

[13] 朱宇涛, 粟毅. 一种M2发N2收MIMO雷达平面阵列及其三维成像方法 [J]. 中国科学(信息科学), 2011, 41(12): 1495-1506.