基于模糊故障树的输油管道压力异常波动分析

王国涛， 姬中元， 李传宪， 陈 赫， 杨 飞

(1.中石化管道储运有限公司，江苏 徐州 221000;2.山东省油气储运安全省级重点实验室 青岛市环海油气储运技术重点实验室，山东 青岛 266580;3.中车青岛四方机车车辆股份有限公司 国家工程研究中心，山东 青岛 266000;4.中石化天然气分公司 华北天然气销售营业部，山东 青岛 266400)

基于模糊故障树的输油管道压力异常波动分析

王国涛1,2， 姬中元2,3， 李传宪2， 陈 赫4， 杨 飞2

(1.中石化管道储运有限公司，江苏 徐州 221000;2.山东省油气储运安全省级重点实验室 青岛市环海油气储运技术重点实验室，山东 青岛 266580;3.中车青岛四方机车车辆股份有限公司 国家工程研究中心，山东 青岛 266000;4.中石化天然气分公司 华北天然气销售营业部，山东 青岛 266400)

针对复杂输油管道压力异常波动事故频发，防控措施效果不理想的现状，应用图论中的故障树分析方法演绎压力异常波动的诱导机制，首次提出并建立了复杂输油管道压力异常波动的故障树模型。以某进口原油管道为例，运用德尔菲法和模糊数学理论求解模型，定性分析与定量计算的结果与工程实际相吻合。运用K均值聚类方法分析典型基本事件的三个重要度，提出了管网压力异常波动的三元决策树结构，为波动事件的分析和防控措施的优化提供了理论依据。以压力异常波动为切入点，在历史数据不完备条件下，为大型复杂输油管道运行安全与完整性管理领域的研究提供了一种新的思路。

复杂输油管道； 压力波动； 故障树； 模糊数学； 决策树

据统计，国内60%以上的原油管道已进入“浴盆曲线”所描述的老龄期[1]，压力异常波动频繁复杂。同时，随着国内原油成品油管道逐渐建设成网，多分输、多注入的液体管道逐渐增多，其复杂性、不确定性更增加了调度人员对异常工况判断的难度，且易引起误判，给国民经济造成重大损失。为了减少管线压力异常波动误判事故的发生，必须对诱导压力异常波动各因素间的逻辑关系进行演绎，理清各种固有或潜在的危险诱因，找出系统的薄弱环节，为压力异常波动的分析和防控措施的制定提供理论依据。

故障树分析法(FTA)是分析大型复杂系统安全性和可靠性的有效工具[2]。目前，有关输油管道安全性的研究主要集中在管道失效[3-5]、管道泄漏[6-8]以及输油泵故障[9-11]等方面，缺乏从系统整体出发对多因素协同作用下压力异常波动产生机制的深入探讨。本文基于故障树分析方法，在资料分析和数据采集的基础上，采用模糊数学理论评估了各底件发生概率的模糊性，运用故障树定性分析和定量计算方法综合演绎了各因素间的逻辑关系。以我国东部某进口原油管道Y为例，提出一种适用于复杂输油管道压力异常波动分析与防控的模型和方法。

1 故障树分析原理

故障树分析是一种系统化的多因素演绎分析方法，其数学基础来源于系统工程中的图论、集合论、概率论、数理统计等思想，在系统可靠性分析、安全性分析和风险评价中具有重要作用和地位。其基本原理是：以系统最不希望发生的事件为目标“由果寻因”，运用逻辑“树”型图逆向演绎顶事件发生过程，分析出故障的根本原因，并深入地揭示出故障的潜在诱因。故障树由各种事件及其逻辑关系组成，故障树分析流程如图1所示。

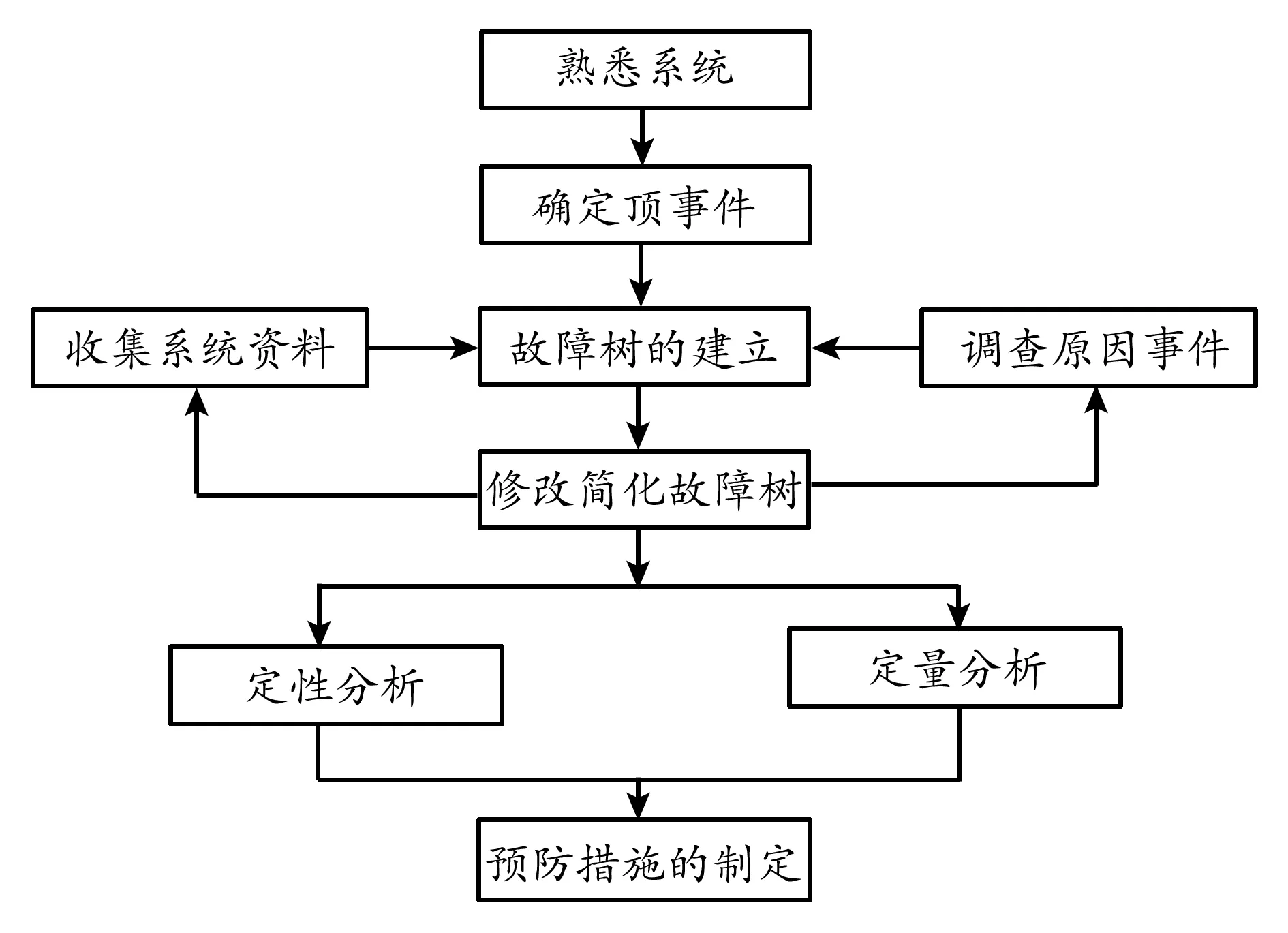
图1 故障树分析流程

Fig.1 Process offault tree analysis

故障树的定性分析和定量计算的主要任务是求取最小割集、最小径集和三个重要度[12]，其概念和计算原理如下：

(1) 最小割集(MCS)是导致顶事件发生的最低限度的基本事件的组合[13]，表征了系统故障的诱发路径，可通过布尔代数法(上行法)或行列式法(下行法)求得。

(2) 最小径集(MPS)是使顶事件免于发生的最低限度的基本事件的组合[13], 表征了故障的有效预防途径。通常把故障树中的“或门”和“与门”互换，转化为对偶的“成功树”，求“成功树”的最小割集,间接获得故障树的最小径集。

(3) 三个重要度的概念与计算

结构重要度：表征基本事件在故障树结构中重要程度的量值[13]，计算式为：

(1)

式中,Ist(i)为第i个基本事件的结构重要度；n为基本事件个数;φ(1,xi)为基本事件状态为1时顶上事件状态；φ(0,xi)为基本事件状态为0时顶上事件状态。

概率重要度：表征基本事件概率对系统故障发生概率影响程度的量值[13]，计算式为：

(2)

式中，Ipr(i)为第i个基本事件的概率重要度；Q为顶事件概率；qi为第i个基本事件的概率。

临界重要度：从敏感性和概率重要性双重角度表征基本事件重要度的量值[13]，计算式为：

(3)

式中，Icr(i)为第i个基本事件的临界重要度。

2 压力异常波动模型的构建

2.1 诱因分析

通常, 管道在稳定状态下运行时，流动液体各个截面上的流速与压力平均值变化较小，可近似视为定常流动。但油品的压缩性[14]、管道的弹性、油流的动能与惯性等内在因素使管道具备了产生压力异常波动的特性与动力。因此，当外因导致管道沿线某点的流动参数发生变化时，管道内部便会出现瞬变压力脉动[15]。瞬变压力叠加在稳态时的压力分布上，便会产生压力异常波动并沿管线传播，影响管道系统的安全运行。

复杂输油管道运行过程中，压力异常波动频繁而复杂，可按如下八大类因素进行演绎分析：M1输油泵操作；M2泄压保护；M3调节阀动作；M4阀门动作；M5过滤器堵塞；M6流量计支路开闭；M7油品切换操作；M8管道泄漏。

2.2 模型建立

为理清压力异常波动的诱导机制，在对国内多条输油管线的资料分析和现场调研的基础上，以管道压力异常波动为顶事件(T)，上述八大类因素为次顶事件(M1，M2，……，M8)，建立故障树模型，如图2所示，基本事件见表1。

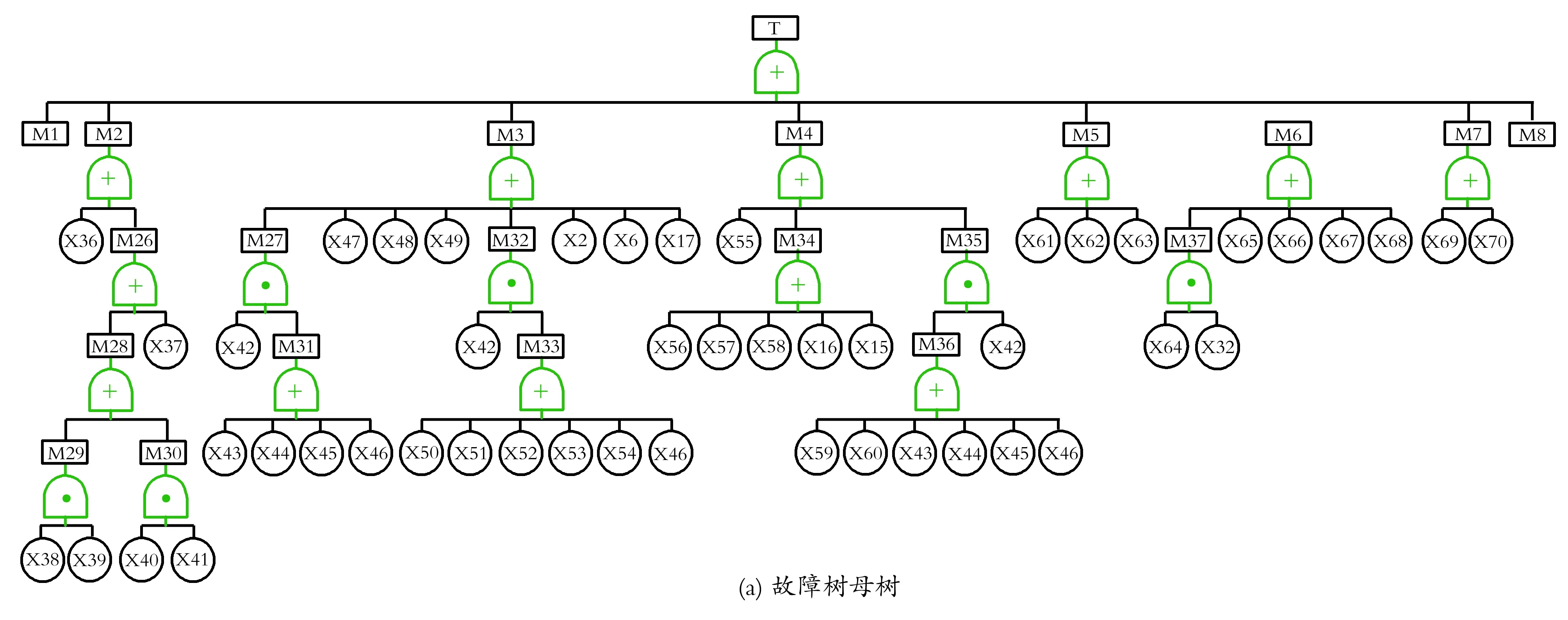
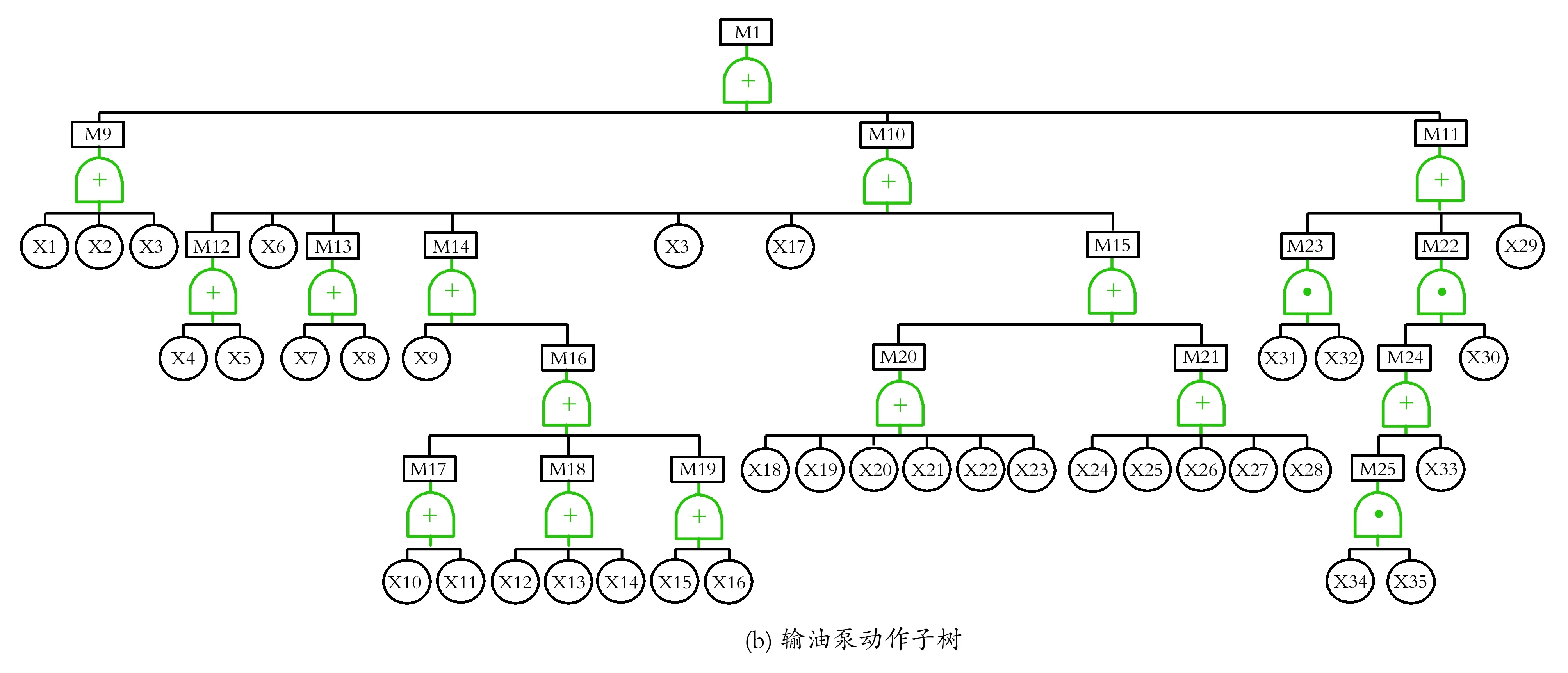
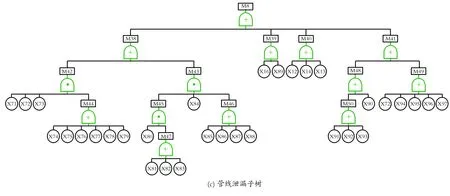
图2 复杂输油管道压力异常波动故障树模型

Fig.2 Fault tree model for abnormal pressure fluctuations of complex pipe network

由图2可以看出，故障树结构中的事件共有6层97种，记为(i=1,2,……,97)。8个次顶事件由“或门”连接，任一方面问题的出现都将导致压力异常波动的产生。逻辑结构包括43个“或门”和12个“与门”，“或门”占比达到78%，“或门”较多而“与门”较少，只要较少数量的基本事件发生，则顶事件就可发生。这一特点与复杂输油管道工程实际相符合。

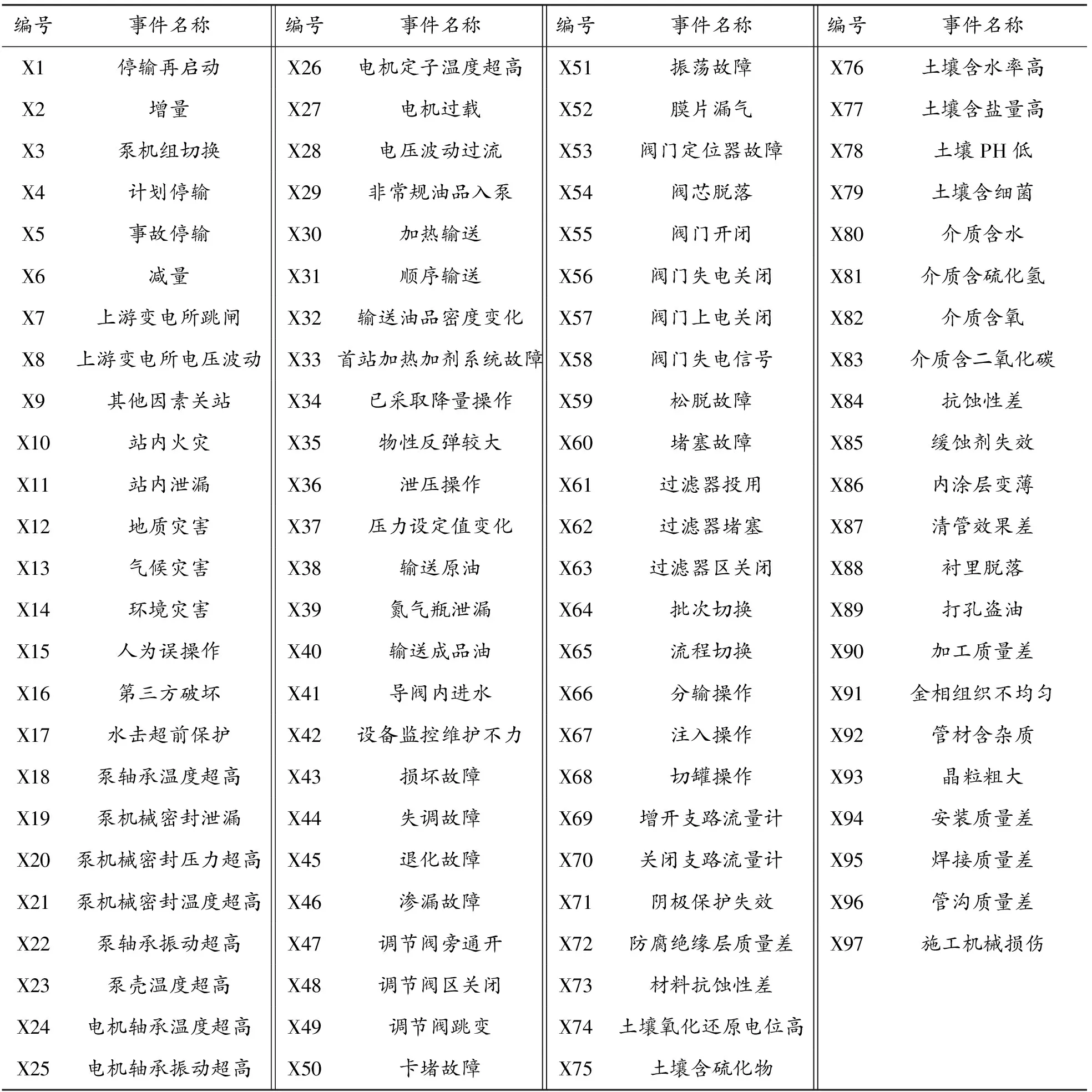
表1 基本事件编号与名称

2.3 定性分析

2.3.1 最小割集计算分析 最小割集是导致顶事件发生的最低限度的基本事件及其组合，表征了系统的危险性。一个最小割集即代表了一种故障模式，从任一方面出发制定相应的措施，都可降低压力异常波动的产生频率。利用布尔代数简化法计算复杂输油管道压力异常波动故障树的最小割集，由式(4)得到86个最小割集，见表2。

T=M1+M2+M3+M4+M5+M6+M7+M8

(4)

该故障树由57个一阶最小割集、16个二阶最小割集、1个三阶最小割集和12个四阶最小割集组成。割集数目相对较多，表明顶事件发生路径较多，也反映了压力异常波动影响因素的复杂性。在数量一定的前提下，基本事件所在割集阶数越小，出现的次数越多，它引发故障的可能性也就越大。因此，为提高管线的可靠性与安全性，应首先考虑发生概率较大或危险性较高的57个一阶最小割集。

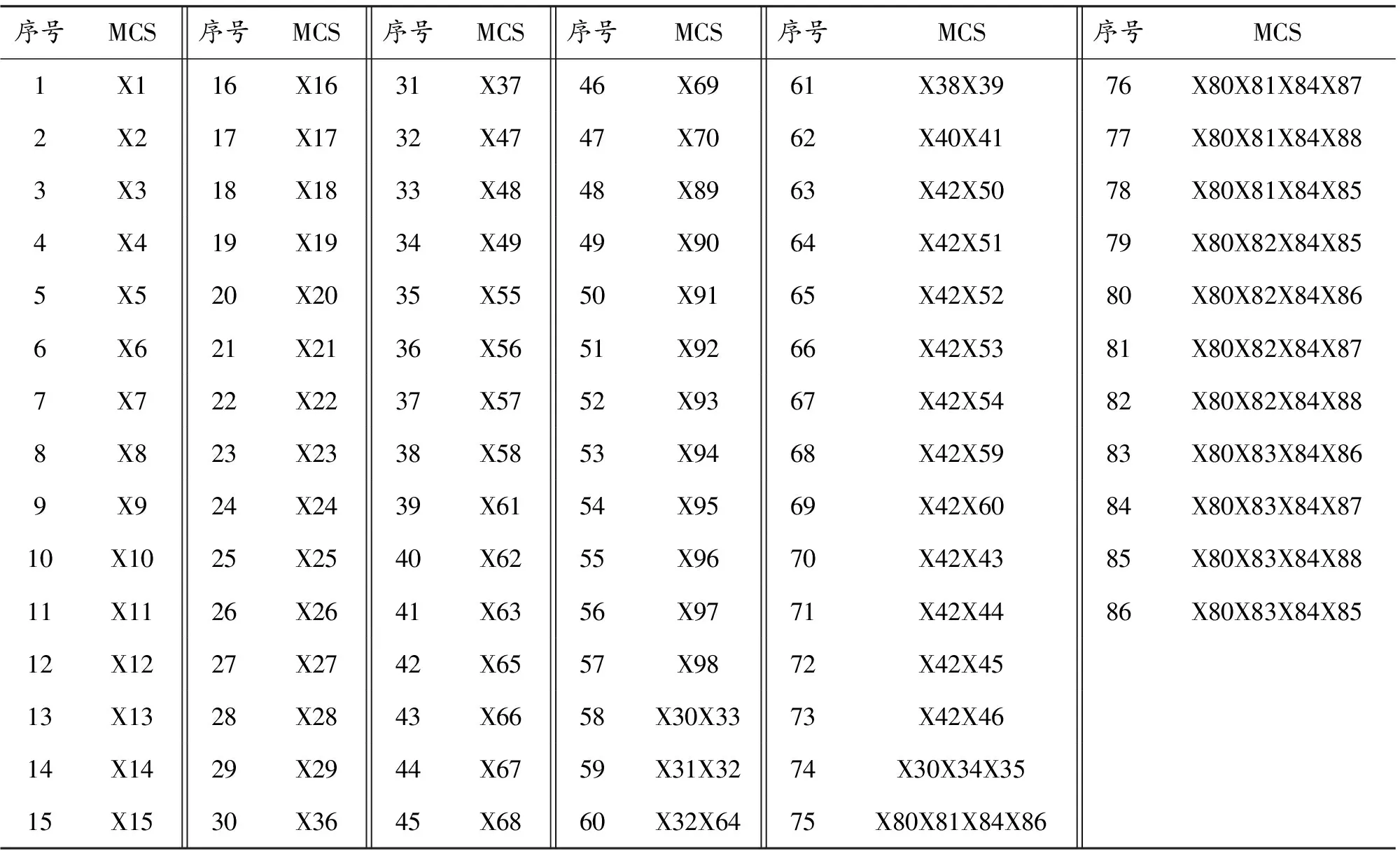
表2 复杂输油管道压力异常波动故障树最小割集

2.3.2 最小径集的计算分析 最小径集是使顶事件免于发生的基本事件及其组合，表征了系统的安全性。把故障树中的“与门”和“或门”对换，将故障树转换为“成功树”，则成功树的最小割集即为故障树的最小径集：

T’=M1’×M2’×M3’×M4’×M5’×M6’×M7’×M8’

(5)

通过计算发现，虽然故障树有64个最小径集，控制顶事件发生的方案较多，但最优方案也高达64阶。要想避免产生压力异常波动，即使按照最短路径也需至少64个基本事件免于发生，这几乎是不可能的。事实上，正常工况的操作同样会产生异常波动，因而管道压力异常波动是无法避免的，与工程实际相符。

3 工程应用实例

为验证故障树结构的合理性，选取我国东部某进口原油管道Y进行实例计算与分析。Y管道采用原油顺序输送，具有分输与注入支线，沿线具有落差大、输油工况多、水力系统及外部环境复杂等特点，压力异常波动频繁(见表3)，误判事故时有发生，严重影响管线的安全、平稳、经济运行。分析该管网压力异常波动的产生机制并采取针对性地防控措施有着迫切的工程需要。

表3 Y管道压力异常波动的频率

3.1 底事件概率的确定

传统FTA通常认为底事件发生概率为精确值。但在实际系统中，事件概念的模糊性、影响因素的复杂多变性以及人为干扰的不可预见性，都使我们难以得到某一特定底事件发生概率的精确值[16]，且其投产较早，管理水平一般，历史数据很不完备，因而无法基于历史故障统计数据进行经典的数理统计分析。鉴于此，本文通过引入集合判断法与模糊集理论相结合的方法确定基本事件的发生概率。

首先采用德尔斐法对引起Y输油管道压力异常波动的基本事件进行主观判断。所选择的专家包括中控调度人员、工程技术人员、现场工作人员以及相关院所的科研人员等。采用模糊数学理论处理专家的定性描述，用三角形模糊数或梯形模糊数代替自然语言[17]。采用的自然语言及其模糊数的表达形式如图3所示。

以Y输油管道“调节阀跳变”这一基本事件(X49)发生概率的求解为例，可按如下步骤进行估算：

(1) 采用德尔斐法[18]给出自然描述

邀请专家组成评估组，对“调节阀跳变”作出主观判断。确定不同专家自身的权重，以便对评判结

果进行加权修正以增加半定量法的置信度。所选的10位专家的权重见表4，评估意见依次为：大、中等、大、小、很大、中等、很大、大、大、很大。

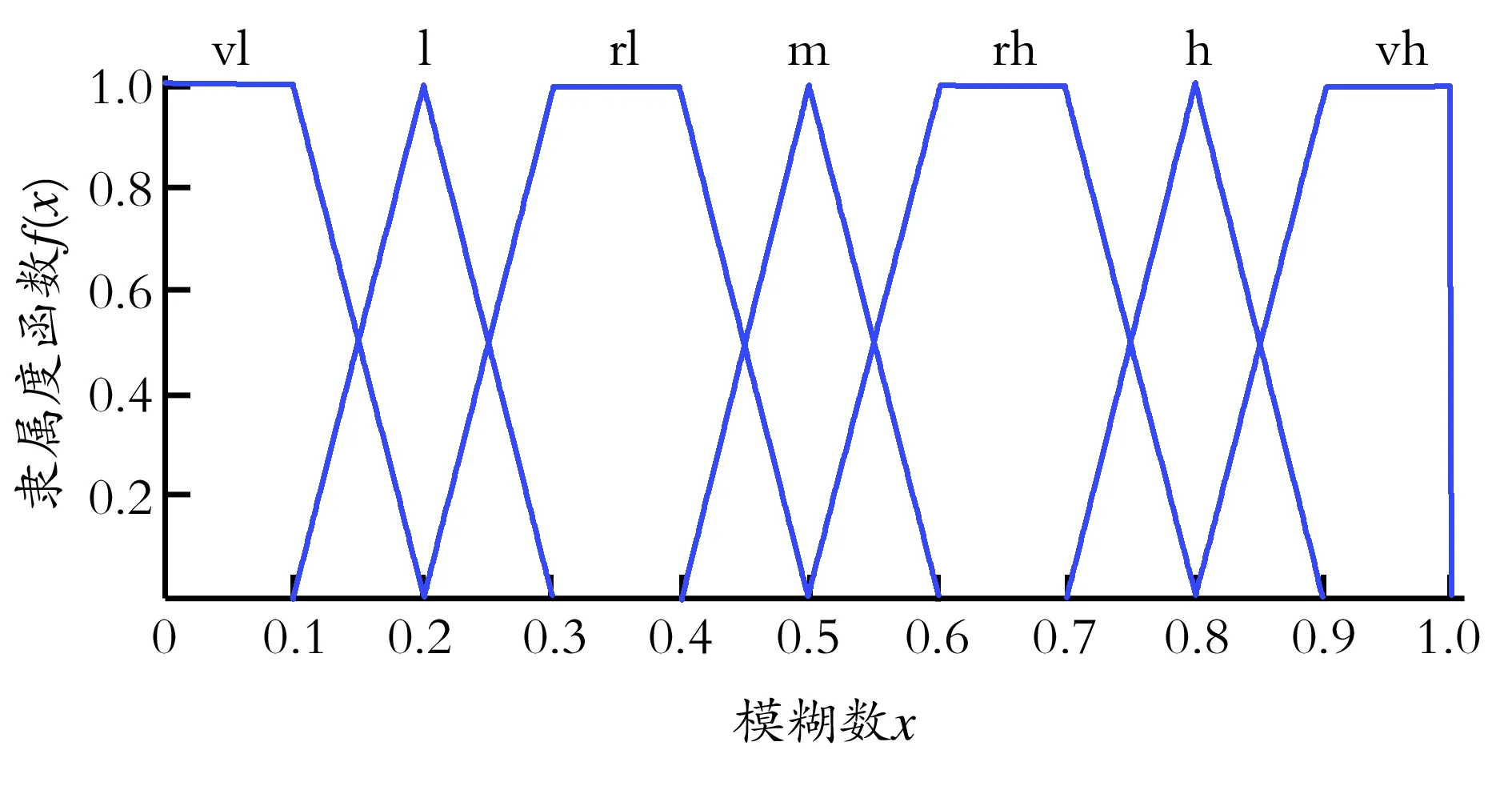
图3 隶属度函数与模糊数

Fig.3 Relationship between fuzzy number and natural language

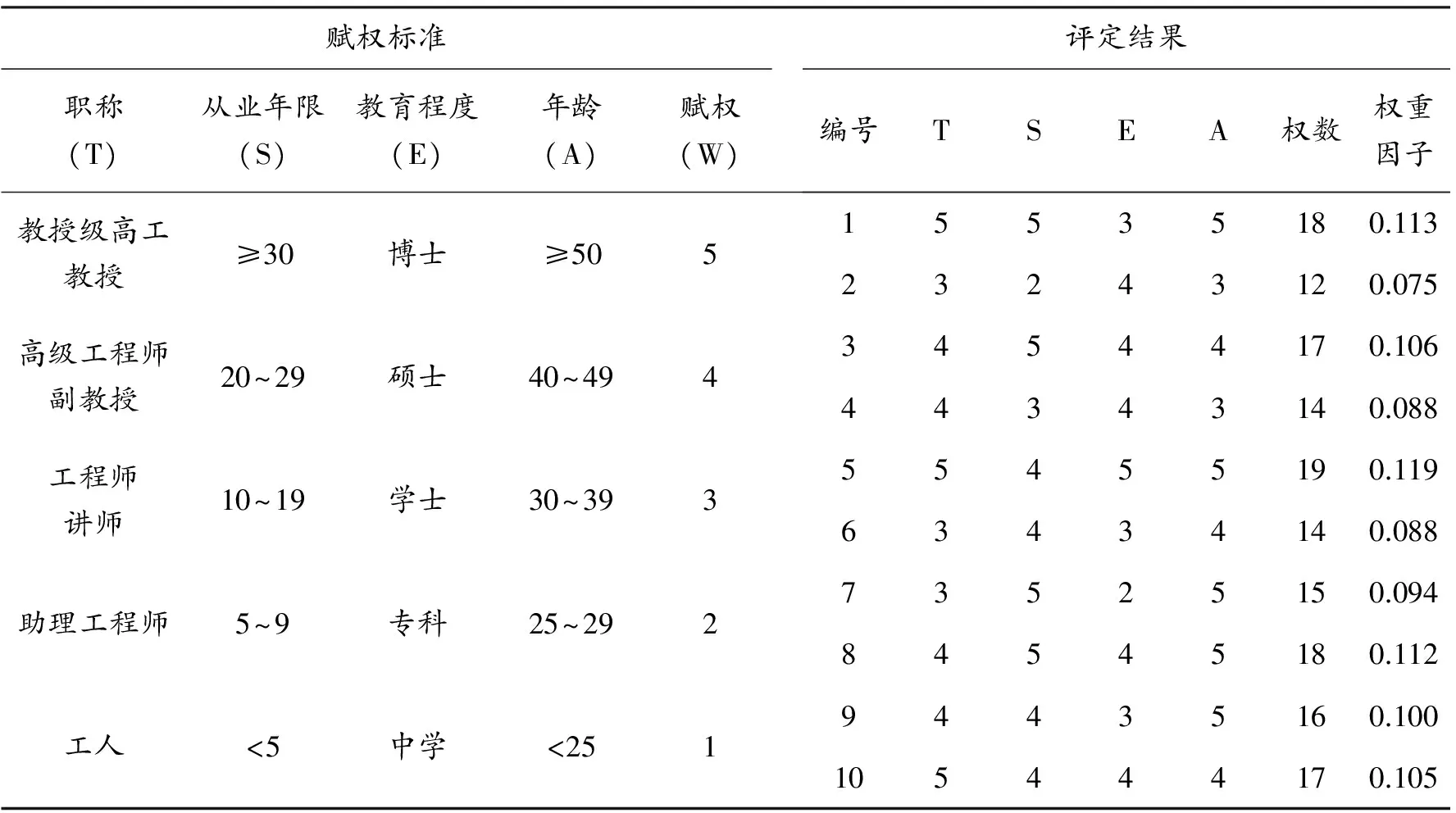
表4 专家权重的评定方法

(2) 把自然语言转化为模糊数

模糊数的表现形式涵盖了10位专家的评估意见。由此得到相对于图3的自然语言模糊数的隶属度函数，见公式(6)、(7)、(8)、(9)。

(6)

(7)

(8)

(9)

式中，下标vh、h、m、l分别表示专家的模糊判断“很高”、“高”、“中等”和“低”。

应用模糊集的α截集[19]并采用一致规则中的线性意见汇集 (The Linear Opinion Pool)[20]方法组合不同专家的意见见公式(10)，其相应模糊数的隶属函数见公式(11)。

f(x)=max[(w5+w7+w10)·fvh(x)^(w1+w3+w8+w9)·fh(x)^(w2+w6)·fm(x)^w4·fl(x)]=[(0.1α+0.631),(0.831-0.068α)]

(10)

(11)

(3) 把模糊数转化为模糊可能性值FPS

由式(11)得到的模糊数依旧是[0,1]上的一个模糊集合。一个模糊数可能代表不同的隶属函数的许多实数，难以在定量分析中对结果进行比较。基于Cheng和Hwang所提出的左右模糊排序法[20], 把模糊数转化为一个清晰值，即模糊可能性值见公式(12)。

FPST(w)=[FPSR(w)+1-

(12)

(4) 模糊可能性值FPS转化模糊故障率FFR

对于故障树的基本事件的发生概率，有的已知其发生概率，有的则是由模糊集理论和德尔菲法结合得到的。为保证模糊故障率和统计故障率之间的

一致性，将模糊可能性值转化为模糊故障率[21]，见公式(13)、(14)：

(13)

(14)

由式(13)、(14)得，模糊故障率为：FFR=2.103 9×10-2，即调节阀跳变的发生概率为：2.103 9×10-2。该过程计算量较大，采用VC编制软件求解见图4，得到所有基本事件的发生概率见表5。

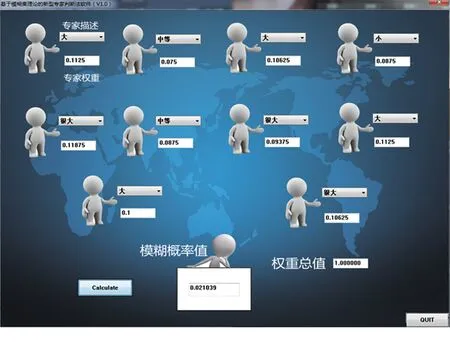
图4 基于模糊集理论的德尔菲法软件

Fig.4 Solution interface of the software

表5 Y输油管道基本事件发生概率表

续表5

3.2 顶事件概率的计算

顶事件概率为基本事件的概率积。由于故障树的最小割集往往是相交的，同一基本事件可以在不同最小割集中反复出现，因而要精确计算顶事件的发生概率就必须用相容事件的概率公式，常用的方法包括布尔真值表算法、最小割集算法和近似算法[2]。布尔真值表通过故障树的结构函数计算顶事件概率，见公式(15)：

(15)

式中，Q为顶事件概率；φ(x)为顶事件状态值，φ(x)=0或φ(x)=1；qi为第i个基本事件的概率；Xi为第i个基本事件的状态值，Xi=0或Xi=1。

对于结构复杂的故障树，一般采用公式(16)的平均近似解：

(16)

式中，K表示割集的数量，Kj、Ks分别表示第j个、第s个最小割集。

由此计算得到Y管道压力异常波动的概率为83.8%，而近五年压力异常波动的概率统计值为86.5%。基于故障树分析方法得到的概率值与工程实际值的相对误差3.22%，在工程允许的范围内。这说明所建立的复杂输油管道压力异常波动故障树结构合理，基于故障树的复杂输油管道压力异常波动分析方法切实可行。若将该管道可控性基本事件的发生概率降低为目前的50%，则压力异常波动的概率将降低为55.8%，约为原来的2/3。因此，有针对性的采取防控措施，变被动维护为主动预防，可以降低Y输油管道压力异常波动的产生频率，从而减少误判及其次生事故的发生。

故障树的各基本事件对顶事件的影响程度不同，重要度从三个方面对这种影响进行了刻画。采用公式(1)—(3),可求得各基本事件的结构重要度、概率重要度和临界重要度。利用K均值聚类算法[22]对三个重要度的计算结果进行分析，可将基本事件分为五类见表6，建立典型事件防控顺序的三元决策树结构见图5，进而针对该复杂输油管道系统提出以下5条压力异常波动的具体防控对策。

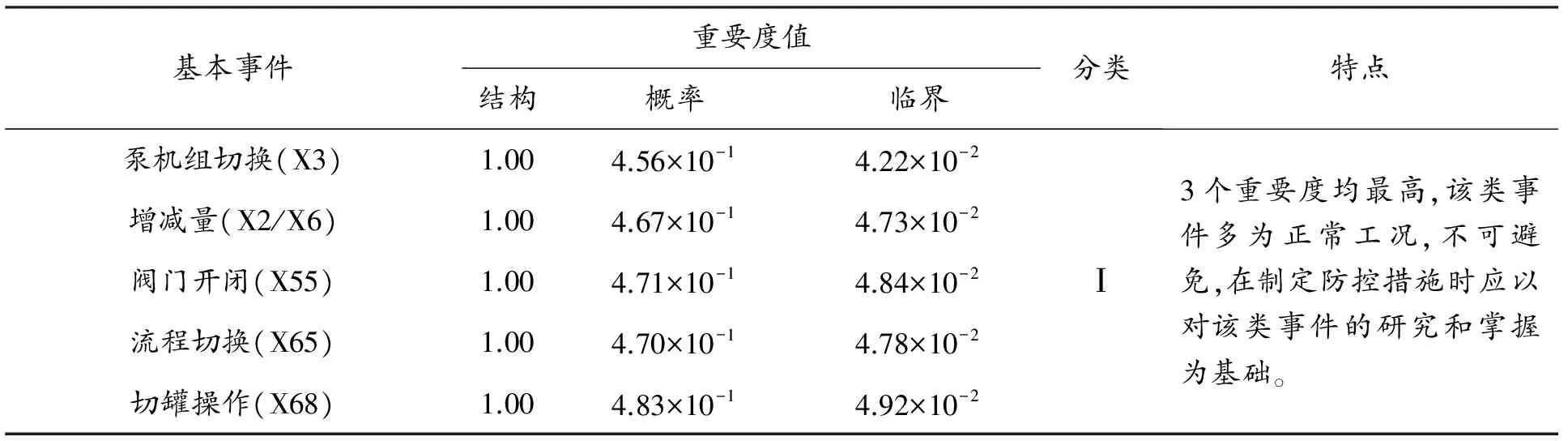
表6 Y管道典型基本事件重要度计算结果及聚类分析

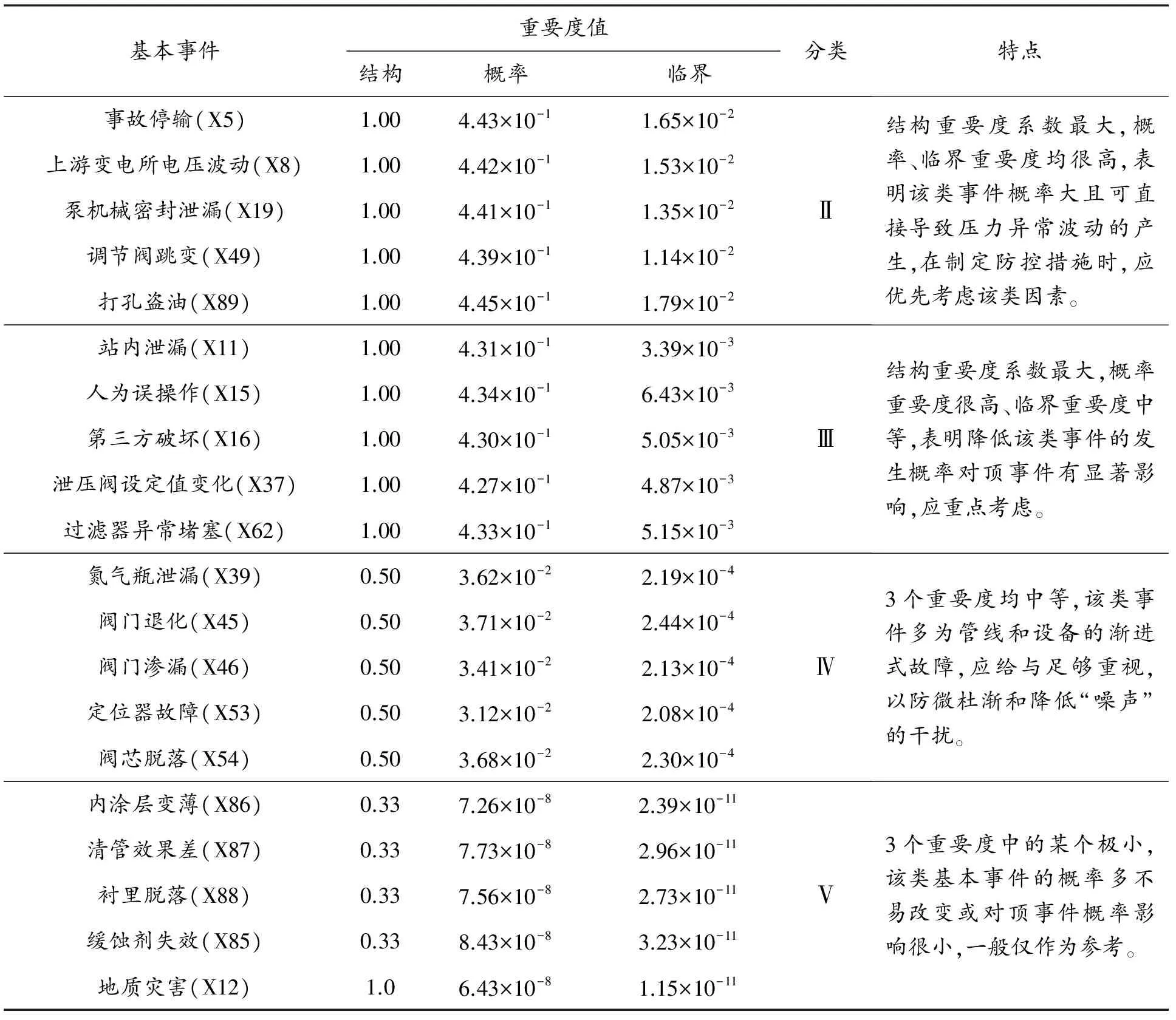
续表6

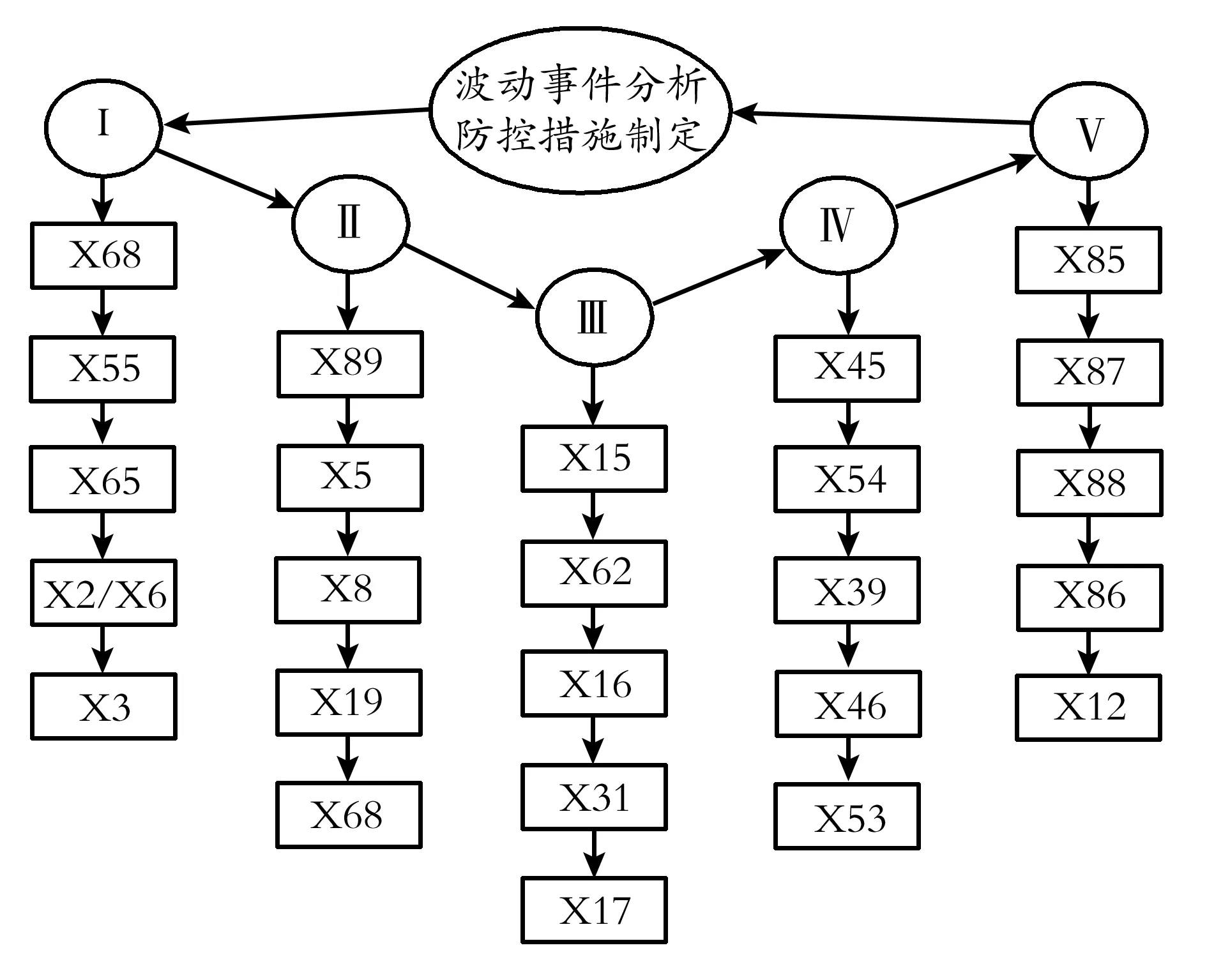
图5 Y管道压力异常波动典型基本事件防控决策树

Fig.5 Typical basic event control sequence decisiontree of Y pipeline

(1) Ⅰ类事件基本属于正常工况，且操作频率极高，其产生的压力异常波动是不可避免的。可通过优化工艺流程减少调泵、调阀、切罐等操作的频次。

(2) Ⅱ、Ⅲ类事件多属于异常工况或紧急工况，管道运行中事故性工况的发生概率较高，但危害性极大。往往导致全线降量或停输，严重的会造成沿线环境污染等次生灾害。建议管输部门日常运行时按照故障树的结构理清诱导机制，在检修期间根据决策树的顺序逐项排查。

(3) Ⅳ类事件多属于设备的渐进式故障。故障停泵参与水击保护程序，可直接引起自保护停泵。阀门等设备的渐进式故障，在短期内不会触发明显的压力异常波动，但设备的定期维护有助于降低渐进式故障产生的压力“噪声”，减轻对在线识别压力波动的干扰。V类事件多取决于管道施工等前期工作并受制于客观条件，因而在故障树中的重要度最小，但合理的改进将有助于延长管道的服役年限。

(4) 控制人为事故。分析结果表明，该管道打孔盗油现象较为严重(X89)，人为误操作(X15)责任事故时有发生。应采取有效措施遏制沿线的打孔盗油行为，并通过规范操作流程，加强安全教育，避免站场误操作造成调控人员的误判，给下游炼厂、油库的计划完成带来不必要的影响。

(5) 根据Y输油管道压力异常波动频繁，误判事故时有发生的实际情况，建议在原有SCADA系统实时数据库的基础上，进一步开发压力异常告警与专家分析系统，采用信号分析和计算智能等在线实时捕捉，识别压力异常波形，并反馈分析结果，从而大大减少误判事故的发生。

4 结论

(1) 通过大量调研和分析，将管网压力异常波动的诱因归纳为八大类，采用树形结构层层演绎其诱导机制。

(2) 首次提出并建立了管网压力异常波动的故障树模型，且该模型具有一定的普适性和广泛的可借鉴性。

(3) 采用德尔菲法和模糊数学理论相结合的方法对基本事件的概率进行求解，通过加权修正增加了半定量法的置信度。

(4) 采用K均值聚类分析三个重要度，首次提出并构建了管网压力异常波动的三元决策树结构，为防控措施的优化提供理论依据，对管线的检修和设备的维护具有指导意义。

(5) 以工况复杂、历史数据不完备的某进口原油管道为例，构建并系统介绍了一种复杂输油管道压力异常波动事件分析与防控优化的模型和方法。

[1] 国静. 油气管道企业长输油气管道突发事件应急管理能力评价[D]. 成都：西南石油大学, 2015.

[2] 孙建刚, 赵桂姿, 滕振超,等. 石油钻机维修可靠性研究[J]. 石油学报, 2002, 23(6):81-84. Sun Jiangang,Zhao Guizi,Teng Zhenchao,et al. Research on the maintenance reliability of thepetroleum drilling rig[J]. Acta Petrolei Sinica, 2002, 23(6):81-84.

[3] 王茜, 赵建平. 海底管道第三方破坏失效状况模糊故障树分析[J]. 天然气工业, 2008, 28(5):109-111. Wang Qian, Zhao Jianping. Fuzzy fault tree analysis on third-party damage failure of submarine pipeline[J]. Natural Gas Industry, 2008, 28(5):109-111.

[4] 霍春勇, 董玉华, 高惠临. 长输天然气管线的故障树研究[J]. 天然气工业, 2005, 25 (10):99-102. Huo Chunyong, Dong Yuhua, Gao Huilin. Fault tree analysis on long-distance nature gas pipeline[J]. Natural Gas Industry, 2005, 25(10):99-102.

[5] Wu X, Xiao C Y, Xu X Y. Research on a nonlinear fuzzy comprehensive assessment method for oil & gas pipeline failure based on fault tree analysis[J]. Applied Mechanics & Materials, 2012, 187(15):304-310.

[6] 张明红, 佘廉. 基于ETA和FTA的输油管道泄漏公共安全事件演化分析[J]. 电子科技大学学报, 2015, 17(3):24-28. Zhang Minghong, She Lian. Analysis of oil pipeline leakage public safety incident evolution based on ETA and FTA[J]. Journal of University of Electronic Science and Technology of China, 2015, 17(3):24-28.

[7] 徐永莉. 基于事故树分析“11·22”输油管道泄漏爆炸事故[J]. 安全, 2015(7):34-37. Xu Yongli. Fault tree analysis on "11·22" pipeline leakage explosion[J]. Safety, 2015(7):34-37.

[8] Alkhaledi K, Alrushaid S, Almansouri J, et al. Using fault tree analysis in the Al-Ahmadi town gas leak incidents[J]. Safety Science, 2015, 79:184-192.

[9] 陈琳, 王国丽, 孟惠荣,等. 抽油泵故障树分析[J]. 石油学报, 1995, 16(3):145-151. Chen Lin, Wang Guoli, Meng Huirong, et al. An analysis of fault tree of an oil-well pump[J]. Acta Petrolei Sinica, 1995, 16(3):145-151.

[10] 王志国, 李东明, 许涛. 抽油泵故障树及模糊综合评判组合分析研究[J]. 石油学报, 2003, 24(6):87-89. Wang Zhiguo, Li Dongming, Xu Tao. Combination of fault tree analysis and fuzzy comprehensive estimation method for oil well pump[J]. Acta Petrolei Sinica, 2003, 24(6):87-89.

[11] 王中辉，朱江，李亚力.钻井泵泵阀的故障树分析及新型泵阀的研制[J].石油化工高等学校学报，2002，15(2)：59-62. Wang Zhonghui,Zhu Jiang,Li Yali. The fault tree analysis of drilling pump valve and the development of the new type of pump valve[J]. Journal of Petrochemical Universities,2002，15(2)：59-62.

[12] 臧艳彬, 王瑞和, 张锐,等. 基于事故树的钻柱失效分析方法[J]. 石油学报, 2011, 32(1):171-176. Zang Yanbin, Wang Ruihe, Zhang Rui, et al. A failure analysis of drill string based on fault tree[J]. Acta Petrolei Sinica, 2011, 32(1):171-176.

[13] 王长申, 孙亚军, 杭远. 基于事故树分析的煤矿潜在突水危险评价研究[J]. 岩石力学与工程学报, 2009, 28(2):298-305. Wang Changshen, Sun Yajun, Hang Yuan. Application of fault tree analysis to risk assessment of potential water-inrush hazards in coal mining[J]. Chinese Jounal of Rock Mechanics and Engineering. 2009, 28(2):298-305.

[14] 范砧, 赵英海. 中国原油压缩性的研究[J]. 石油学报, 1985,6(2):99-107. Fan Zhen,Zhao Yinghai. Compressibility study of Chinese crude oils [J]. Acta Petrolei Sinica, 1985,6(2):99-107.

[15] Afshar M H, Rohani M, Taheri R. Simulation of transient flow in pipeline systems due to load rejection and load acceptance by hydroelectric power plants[J]. International Journal of Mechanical Sciences, 2010, 52(1):103-115.

[16] 董玉华, 高惠临, 周敬恩,等. 长输管线失效状况模糊故障树分析方法[J]. 石油学报, 2002, 23(4):85-89. Dong Yuhua, Gao Huilin, Zhou Jingen, et al. Fuzzy fault tree analysis method for assessing oil and gas pipeline’s fault[J]. Acta Petrolei Sinica, 2002, 23(4):85-89.

[17] Chen S J, Hwang C L. Fuzzy multiple attribute decision making.[J]. Lecture Notes in Economics & Mathematical Systems, 1992, 11(1):102-106.

[18] Ferri C P, Prince M, Brayne C, et al. Global prevalence of dementia: a Delphi consensus study[J]. Lancet, 2005, 366(2):2112-2117.

[19] Lin C T, Wang M J J. Hybrid fault tree analysis using fuzzy sets[J]. Reliability Engineering & System Safety, 1997, 58(3):205-213.

[20] Bolger D, Houlding B. Reliability updating in linear opinion pooling for multiple decision makers[J]. Proceedings of the Institution of Mechanical Engineers Part O Journal of Risk and Reliability, 2016,230(3):309-322.

[21] Onisawa T. An approach to human reliability in man-machine systems using error possibility[J]. Fuzzy Sets & Systems, 1988, 27(2):87-103.

[22] Caron E. A self-stabilizing k-clustering algorithm for weighted graphs[J]. Journal of Parallel & Distributed Computing, 2010, 70(11):1159-1173.

(编辑 王戬丽)

Abnormal Fluctuations Analysis for Pipe Network SystemBased on the Fuzzy Fault Tree

Wang Guotao1,2， Ji Zhongyuan2,3， Li Chuanxian2， Chen He4， Yang Fei2

(1.SinopecPipelineStorageandTransportationBranchCompany,XuzhouJiangsu221000,China;2.ShandongProvincialKeyLaboratoryofOil&GasStorageandTransportationSafety,QingdaoKeyLaboratoryofCircleSeaOil&GasStorageandTransportationTechnology,QingdaoShandong266580,China;3.EngineeringResearcherCenter,CRRCQingdaoSifangCo.,Ltd.,QingdaoShandong266000,China;4.HuabeiSalesDepartment,SinopecGasCompany,QingdaoShandong266400,China)

Given the frequent accidents attributed to abnormal pressure fluctuation and the less effectiveness of preventive measures of complex pipe network, the FTA method of graph theory was applied to solve this problem. Induced mechanism of abnormal pressure fluctuations was interpreted and the FTA model of pressure abnormal fluctuations in complex pipeline network was firstly proposed and established in this paper. An imported crude oil pipe network was taken as a case study by using the Delphi method and fuzzy mathematics theory to solve the model. Results agree well with the actual statistics. Then K-means clustering method was carried on to analyze the three importance of typical basic events and the three-tier structure of the abnormal fluctuations is proposed using the DTA method, which lies a theoretical basis for the analysis on abnormal events as well as the optimization of the prevention and control measures. This paper mainly offers a new research idea in the field of operation security and integrity management of the large, complex pipe network especially when the historical data is far from complete.

Complex pipe network; Pressure fluctuation; FTA; Fuzzy sets; DTA

2016-12-23

2017-01-04

国家自然科学基金(51204202)；山东省自然科学基金 (ZR2012EEQ002)；中央高校基本科研业务费专项资金 (14CX02210A，15CX06072A)。

王国涛(1965-)，男，硕士，高级工程师，从事油气长距离管输方面的研究；E-mail：hdwanggt@163.com。

李传宪(1963-)，男，博士，教授，博士生导师，从事油气长距离管输等方面的研究; E-mail：lchxian@upc.edu.cn。

1006-396X(2017)02-0060-11

投稿网址：http://journal.lnpu.edu.cn

TE88

A

10.3969/j.issn.1006-396X.2017.02.012