薄板焊接变形高精度预测方法的研究

梁伟，马峰，张渝，村川英一

（1.重庆交通大学机电与车辆工程学院，重庆400074；2.大阪大学接合科学研究所，日本大阪567-0047）

薄板焊接变形高精度预测方法的研究

梁伟1，马峰1，张渝1，村川英一2

（1.重庆交通大学机电与车辆工程学院，重庆400074；2.大阪大学接合科学研究所，日本大阪567-0047）

采用固有应变方法预测焊接变形时，传统方法是把纵向收缩、横向收缩和角变形这三成分作为接头的固有变形来估算焊接变形。但是，由于薄板的刚度低，在纵向方向上的弯曲变形也较明显，采用传统方法会影响薄板焊接变形的预测精度。为提高精度，文章对传统的方法进行了改进，开发了包括考虑纵向弯曲在内的四成分固有变形数值计算方法来预测薄板焊接变形。数值模拟结果表明：运用该方法预测薄板的焊接变形时，比传统的方法有更高的精度，而且预测结果与热弹塑性有限元的模拟结果十分吻合。

薄板焊接接头；固有变形成分；焊接变形；预测精度

0 引言

近年来，薄板焊接结构件在船舶建造，特别是军船、小型船舶和船体上层建筑中的运用越来越广泛。由于薄板焊接时易产生较大的焊接变形，而影响焊接变形的因素错综复杂，薄板焊接变形的控制仍是造船中的难题之一。因此，为了实现精度造船，研发高精度的薄板焊接变形预测方法具有重要意义。

目前，通常有两种基于有限元理论的数值模拟方法可以用来预测焊接变形：一是热弹塑性有限元方法；另一是基于固有应变理论的弹性有限元方法[1]。一般来说，热弹塑性有限元方法能较忠实地再现焊接加热和冷却过程中温度、应力和应变的变化过程，所以，作为一种高精度的预测技术，该方法被广泛用于焊接接头的变形预测。但是，采用该方法预测焊接变形时，有两个条件是至关重要的：其一是必须知道材料的高温热物理参数和力学性能参数，其二是需要建立合理的热源模型和材料模型来准确描述在焊接过程中的热—冶金—力学耦合行为。对于许多先进结构材料而言，由于材料的高温性能参数匮乏，开发精确的材料模型比较困难，加之采用该方法需要较长的计算时间，因此，该方法在工程应用上有较大的局限性。为了克服热弹塑性有限元方法的局限性，研究者开发了基于固有应变理论的弹性有限元方法来预测焊接变形[2-4]，近年来，这一方法越来越受到研究者的重视，并取得了较大的进展。

从理论上讲，固有应变有限元预测方法是一种弹性有限元数值计算方法，其原理是将焊接加热及冷却过程中产生的分布在焊缝周围的残余塑性应变作为初始应变代入到弹性有限元模型中,通过弹性计算求解变形场和应力场。显然，采用该方法预测焊接变形时，固有应变等效载荷的近似程度决定了预测精度。

目前，在预测大型复杂结构的焊接变形时，通常采用纵向收缩、横向收缩和角变形等三成分的固有变形来近似表征典型焊接接头的固有变形[5-6]。然而，与中厚板比较，薄板焊接结构件刚度相对较低，因此纵向弯曲更为明显。为了提高采用固有应变法预测薄板结构件焊接变形的精度，本文提出了考虑纵向弯曲成分的固有应变数值模拟方法来计算薄板的焊接变形。为了验证所提方法的有效性和计算精度，首先,基于ABAQUS软件，采用微小变形理论和大变形理论分别对低碳钢薄板对接接头的焊接变形进行了数值模拟，然后，通过比较微小变形和大变形理论下得到沿焊缝方向上的固有变形的分布规律，提出了四成分固有变形分布的简化模型，并利用该简化模型对薄板的焊接变形进行了预测；最后，通过比较固有应变法和热弹塑性有限元分析的模拟结果，验证了固有变形分布简化模型的精度。结果表明：本文提出的四成分固有变形简化模型与传统的三成分方法相比具有更高的计算精度。

1 热弹塑性有限元计算模型及结果分析

首先采用热弹塑性有限元方法得到薄板对接接头的残余塑性应变。为了使解析结果更具有普遍性，热弹塑性有限元分析考虑了线能量、部分焊的影响，焊接变形位移场分别采用微小变形理论和大变形理论进行了预测。

部分焊平板对接接头的尺寸及边界条件如图1所示。模型的尺寸为：L=200 mm，B=100 mm，h= 3.0 mm。焊接热源采用Goldak热源[7]。部分焊的长度为对接接头中段的100 mm。由于平板在结构上对称，故选取半板建模，以减少计算量。在计算应力场时，为防止薄板的刚体位移，在对称面上对Y方向进行了拘束。其余的拘束位置如图1所示。随温度变化的热物理参数及机械性能参数参见文献[8]。

作为解析结果的一例，图2表示了入热量Q为133.2 J/mm时薄板沿厚度方向的变形结果。其中图2（a）采用微小变形理论，图2（b）采用大变形理论进行了计算。从图2可知：对于薄板而言，采用不同的变形理论得到的焊接变形结果差异显著，采用微小变形理论得到的变形呈碗型，而采用大变形理论得到的变形呈鞍型。该结果表明：对于3 mm以下的薄板，一般需要考虑几何非线性，即应该采用大变形理论来预测薄板的焊接变形。

图1 模拟对象的尺寸和边界条件Fig.1 Dimension and boundary conditions

图3表示了薄板中央断面上的纵向残余塑性应变分布。从图中可以看到，尽管板厚只有3 mm，但纵向塑性应变在板厚方向上的分布是不均一的，这种不均匀性正是产生纵向弯曲的主要原因。在考察薄板焊接变形时，与中、厚板不一样，由于其自身弯曲刚度小，因此，纵向弯曲也是一个必须考虑的要求。

图3 中央断面上分布的塑性应变Fig.3 Longitudinal plastic strain distribution in the mid-section

2 固有变形分布及简化模型的建立

薄板焊接结构件由于刚性较差，在焊接方向上弯曲变形的特征相对突出，为提高固有应变法预测焊接变形的精度，本研究提出在传统三成分的固有变形的基础上添加纵向弯曲成分，用四种固有变形，即纵向收缩横向收缩）、纵向弯曲）和横向弯曲）表示薄板的变形。这四个成分的固有变形可由方程式（1）-（4）定义。

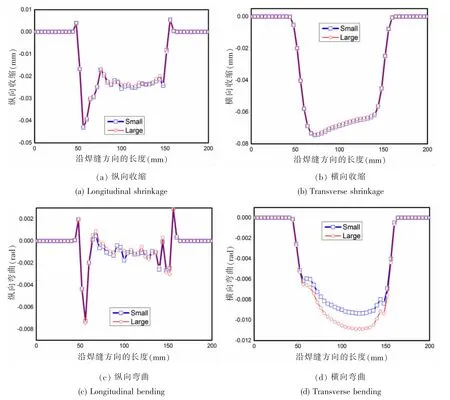
图4 固有变形的分布特征Fig.4 Distributions of inherent deformation components

表1 固有变形各成分的平均值Tab.1 Average value of inherent deformation

从图4中还可以看到，部分焊的固有变形的分布特征和贯通式焊接有相似之处：除焊接始终端之外，固有变形各成分的大小沿焊接线方向的变化量相对较小。而且，固有变形的分布区域和焊接长度近似相等。利用沿焊接线方向固有变形的分布形态较单纯的特征，本文提出了用固有变形的平均值来代替沿焊缝方向上固有变形分布值的近似方法。如果利用固有变形的平均值预测的焊接变形与利用焊缝方向上固有变形分布值得到的变形结果吻合较好的话，不仅可以很方便地将固有应变导入大变形有限元模型中去，大幅减少输入数据，而且也能使固有变形数据库变得更加的便捷可靠。固有变形各成分的平均值如表1所示。

3 采用固有应变法预测焊接变形

理论上，只要固有变形的近似方法得当，采用固有应变法预测的焊接变形就能再现热弹塑性解析的变形结果。根据这一理论，本文采用固有应变法考察了分别导入下述三组固有变形值时薄板的焊接变形：①利用四成分的沿焊缝方向的固有变形分布值；②利用三成分的固有变形平均值；③利用四成分的固有变形平均值。

作为解析结果的一例，采用大变形理论得到的沿厚度方向上焊接变形分布如图5所示。该云图为导入四成分固有变形平均值时得到的变形。

为了考察导入上述三种不同类型固有变形情况下预测的焊接变形的差异，本研究对比了四种情况下沿中央断面上焊接变形的大小。其结果如图6所示，由图6可知，用4成分固有变形平均值算得的中央断面上的变形分布与用固有变形的分布值得到的结果和热弹塑性分析的结果非常吻合，而采用3成分固有变形平均值算得的变形量与热弹塑性分析的预测结果却有较大的差异。

图5 采用固有应变法预测焊接变形Fig.5 Welding distortion using elastic FEM

图6 中央断面上变位Fig.6 Comparison of deformation

4 结论

（1）本文提出了包括考虑纵向弯曲在内的四成分固有变形来表征薄板焊接变形的方法。计算结果表明：采用四个成分固有变形方法计算得到的焊接变形比采用三成分固有变形方法得到的焊接变形有更高的精度，即更吻合热弹塑性有限元的计算结果。

（2）利用各固有变形平均值来代替沿焊缝方向上各成分的固有变形分布值对焊接变形进行预测时，计算精度损失很小。因此，该方法是一种简便有效的方法。

（3）部分焊接的固有变形的分布特征和贯通式焊接有相似之处。即固有变形各成分沿焊接线方向的分布值虽然发生变化，除焊接始终端除外，焊接线中央端各值的变化量很小。而且，固有变形的分布区域和焊接长度近似相等。这一分布特征是四成分固有变形平均值可以利用的前提条件。

（4）在相同线能量的情况下，虽然基于小变形理论和大变形理论得到的接头变形不论是在大小上还是在分布形态上都有较明显的差异，但是两者的各固有变形成分却差别很小。

（5）对板厚小于3 mm的薄板结构件，几何非线性对焊接变形的影响较大。为了准确把握焊接变形的大变形特征，在采用固有应变法预测焊接变形时应和采用热弹塑性理论时一样，有必要采用大变形理论对焊接变形进行预测。

[1]Ueda Y,Murakawa H,Ma N X.Welding deformation and residual stress prevention[Z].ELSEVIER,2012.

[2]梁伟,夏洋,等.焊接变形的高精度测量方法及预测方法研究[J].机械工程学报,2016,52(8)：65-77. Liang wei,Xia Yang,et al.Investigation on high-precision methods to measure and predict welding deformation[J].Journal of Mechanical Engineering,2016,52(8)：65-77.

[3]汪建华,陆皓,魏良武.固有应变有限元法预测焊接变形理论及其应用[J].焊接学报,2002,23(6)：36-42. Wang jianhua,Lu hao,Wei liangwu.The prediction of welding deformation theory and its application based on the inherent strain finite element method[J].Transactions of the China Welding Institution,2002,23(6)：36-42.(in Chinese)

[4]梁伟,邓德安,Murakara Hidekazu.铝合金薄板固有变形逆解析方法的研究与开发[J].中国有色金属学报,2015(11)：3011-3018. Liang Wei,Deng Dean,Murakara Hidekazu.Investigation and develepment of inverse analysis method to estimate inherent deformation of Al-alloy thin-plate joint[J].The Chinese Journal of Nonferrous Metals,2015(11)：3011-3018.

[5]周宏,罗宇,蒋志勇,马坤明.大型船舶结构焊接变形固有应变法预测研究[J].江苏科技大学自然科学版,2010, 24(2)：134-138. Zhou Hong,Luo Yu,Jiang Zhiyong,Ma Kunming.Prediction of welding deformation of large complicated structure based on inherent strain methods[J].Journal of Jiangsu University of Science and Technology(Natural Science Edition),2010,24 (2)：134-138.(in Chinese)

[6]周宏,罗宇,蒋志勇.基于固有应变的船体总段船台合拢焊接变形预测研究[J].船舶力学,2013,17(10)：1153-1158. Zhou Hong,Luo Yu,Jiang Zhiyong.Prediction of welding deformation of block construction of hull based on inherent strain method[J].Journal of Ship Mechanics,2013,17(10)：1153-1158.

[7]Goldak J,Chakravariti A,Bibby M.A new finite element model for welding heat sources[J].Metallurgical Transactions, 1984,15：299-305.

[8]Deng D,Murakawa H.Prediction of welding distortion and residual stress in a thin plate butt-welded joint[J].Comput Mater Sci,2008,43(2)：353-65.

Developing an accurate computational approach to predict welding deformation in thin-plate joint

LIANG Wei1,MA Feng1,ZHANG Yu1,MURAKAWA Hidekazu2
(1.College of Mechatronics&Automotive Engineering,Chongqing Jiaotong University,Chongqing 400074,China; 2.Joining and Welding Research Institute,Osaka University,567-0047,Japan)

When the elastic finite element method based on inherent strain theory is used to predict welding deformation,longitudinal shrinkage,transverse shrinkage and angular distortion are usually taken as main initial strain components to estimate welding deformation,whereas the longitudinal bending component is often neglected because its magnitude is very limited in many cases.However,if the method without considering longitudinal bending is employed to predict welding distortion for a thin-plate joint,it is possible that a large error will generate because the stiffness of thin-plate structure is relatively small and its outof-plane deformation is sensitive to the longitudinal bending.In this study,the traditional method above is improved,and a computational approach with considering four components including the longitudinal bending was developed to predict welding deformation for thin-plate structure.Numerical results show that the prediction accuracy of the newly developed method is higher than the traditional method.

thin-plate welded joint;inherent deformation components;welding distortion; predict accuracy

TG115.25

A

10.3969/j.issn.1007-7294.2017.04.008

1007-7294（2017）04-0437-06

2016-10-22

国家自然科学基金（51375518）/留学回国人员科研启动基金资助

梁伟（1968-），女，博士，教授，硕士生导师，E-mail：wliangspace@163.com；村川英一（1951-）男，博士，大阪大学教授，博士生导师。