基于KD树的规则格网DEM插值技术

黄 艳，卢学良

1.西安测绘研究所，陕西 西安，710054;

2.地理信息工程国家重点实验室，陕西 西安，710054

1 引 言

数字高程模型(digital elevation model，DEM)作为一种表达地形的数学模型，自1958年由美国麻省理工学院Miller教授提出以来，由于其表达方式直观多样、便于更新等优势，已经在测绘导航、农林规划、地学分析等领域得到了广泛的应用和研究，成为国家经济建设以及国防建设的重要基础数据之一[1]。DEM的生产途径多种多样，目前应用最为广泛、生产效率最高的方法一般是通过航空航天摄影测量、合成孔径雷达干涉测量或是机载激光扫描等方式获取地形地物的点云数据，然后通过内插的方式获得规则格网的DEM[2，3]。在这些方法中，插值是DEM生产的重要环节，常用的DEM插值算法有反距离加权插值算法、谢别德插值算法和径向基函数插值算法等[4，5]，这些算法无不是利用待插值点邻域范围内的已知采样点通过特定的加权方式完成插值。因此，邻域采样点的获取是完成插值的前提，而为了高效获取待插值点的邻域采样点，一般要对点云建立空间索引，常用的空间索引方法为栅格法。本文在深入分析栅格法索引的基础上，引入了KD树来实现邻域点的快速获取，并通过试验对两种空间索引的效果进行了对比分析。

2 DEM插值

DEM插值是根据已知采样点的高程值去估计未知插值点高程值的过程[6]，其主要用于缺值估计、等值线内插和离散点云数据的格网化[7]。DEM插值可以通过已知采样点来估计未知插值点，主要是因为地形具有空间异质性和空间相关性等基本特征，使得利用一些空间位置合理的采样点(一般为邻域采样点)获得对地形表面相对精确的描述成为可能。

2.1 邻域采样点的获取

(1)栅格法索引及其存在的问题

在对大数据量的地面点云进行插值时，插值点邻域采样点的获取一般不宜采用全局搜索的方法。为了提高搜索效率，首先要建立点云数据的空间索引，常用的空间索引方法为栅格法。

栅格法的基本思想如图1所示，首先输入点云数据，在确定点云数据的平面范围后，将该平面区域按照设定的尺度栅格化，栅格单元一般为正方形，然后将各个小栅格与其内包含的点关联起来。对于待插值点，在确定该点所在的栅格后，通常该栅格及其8邻域栅格所包含的点即为待插值点的候选邻域采样点，最后经过距离约束或其他方式即可筛选出邻域采样点。

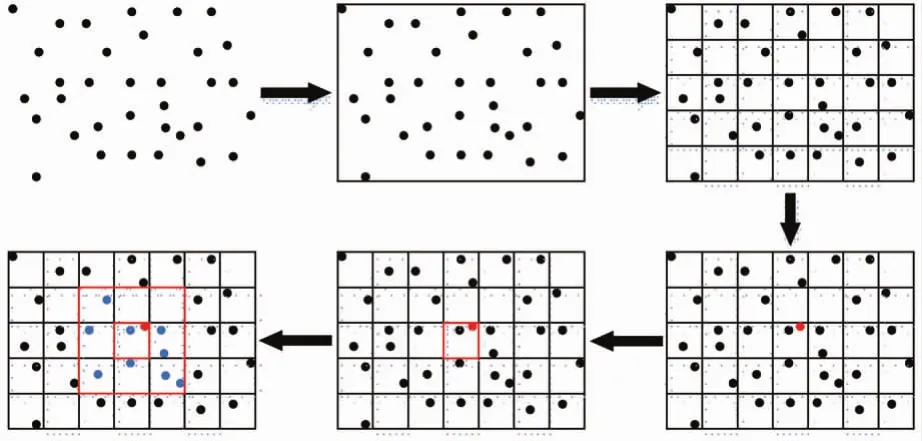
图1 栅格索引建立及检索流程

利用栅格法建立空间索引主要有两个要点：一是栅格大小的确定;二是待插值点搜索范围的确定，即待插值点所在栅格的邻域栅格的范围。其中栅格的大小与DEM的分辨率有关，一般是DEM分辨率的若干倍。而邻域栅格的选择范围一般是其8邻域，当然也可以向外扩充，原则上是栅格越大，邻域的选择范围越小，栅格越小，邻域的选择范围越大。

然而利用栅格法作为空间索引，可能存在某些点比部分邻域采样点距离待插值点更近的情况。如图2所示，显而易见的是doutside＜dinside，这样很可能会导致计算出的待插值点的若干个最近邻点不够准确(并非最邻近点)，进而会影响最终的插值精度。

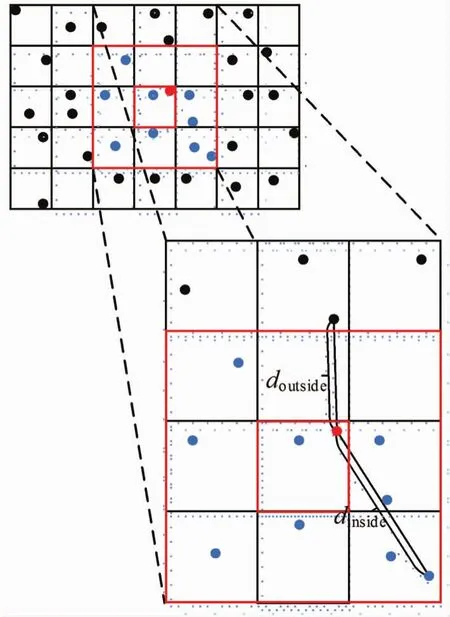
图2 邻域栅格的内点与外点距离示意

目前有两种办法来解决上述情况。第一种方法是在DEM插值点设定某个距离阈值d，如果某些最邻近采样点与待插值点之间的距离大于d，那么它将会被排除。因为距离较远的采样点可能并不能提高待插值点的插值精度，甚至会有所损害，基于这点考虑，将栅格的边长设置为d，便可以规避上述问题，但这样会明显降低空间索引的效率。另一种方法是如果理想中的邻域栅格的选择范围是其8邻域，在实际处理中把选择范围扩大到24邻域，可以在很大程度上避免上述问题(并不能完全规避)，但同样会降低空间索引的效率。

(2)KD树索引

鉴于上述问题，本文在空间索引上使用了KD树。KD树(K-Dimension tree)最早由斯坦福大学的Jon Bentley教授在论文中提出[8]。它是一种应用于高维空间的数据索引结构，采用分而治之的思想将整个空间数据集在K维空间按照一定的规则顺次划分为若干个小空间。二维KD树的构建如图3所示。首先红色的线条将点集分成两个部分，然后每个子块被蓝色线条分别分成两个部分，接着按照绿色线条、紫色线条、浅蓝色线条的顺序依次将子块划分，直至子块中的点集规模小于局部规模阈值。KD树实际上就是决策树，每次找区分度最大的一条轴线进行二分，二分至叶子节点只包含一个点。在查找最邻近点时，先找到叶子节点，然后回溯其祖先节点，以这个点的距离剪枝搜索，最终找到符合要求的若干个最邻近点。

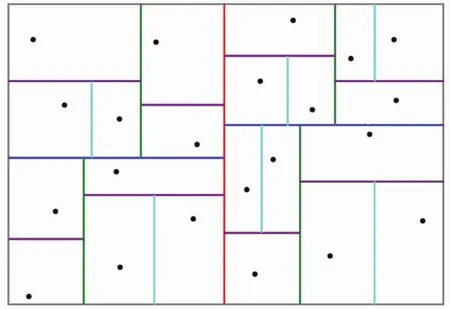
图3 二维KD树[9]

2.2 常用的插值算法

目前常用的插值算法有反距离加权插值算法、谢别德插值算法和径向基函数插值算法等。

(1)反距离加权插值算法

反距离加权插值算法是根据相近相似的原理，对每个采样点赋予一定的权重，权重随着采样点与插值点之间距离的增加而减小。任一插值点处的值是各采样点加权之和，如式(1)所示。

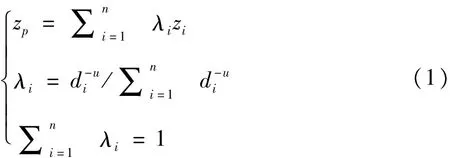
其中，zp为插值点的高程值;λi为第i个点的权重;di为第i个采样点到插值点的距离;d-u为距离衰减函数，幂指数u具有随着距离的增加而减小其他位置影响的作用，通常取值为1或2。

(2)谢别德插值算法

谢别德插值算法本质上是一种标准的导数距离加权过程，权函数如式(2)所示。

其中，wi为权重;di为第i点距待插值点的距离;r为调整距离。

(3)径向基函数插值算法

径向基函数插值算法是一系列用于精确插值算子的统称，其插值原理是任何一个表面都可以用多个曲面的线性组合去逼近。通常情况下，径向基函数插值算法可以表述为两部分之和，如式(3)所示。

其中，zp为插值点的高程值;λi为i第个点的权重;di为第i个采样点到插值点的距离;φ(di)为径向基函数;fi为“趋势”函数，是次数小于m的基本多项式函数。

3 试验与分析

3.1 试验方案

试验一：通过对前述两种空间索引的对比分析，测试空间索引效果。试验环境为Intel(R)Xeon(R)CPU E5-2630 v3(2.4GHz)，32G内存，操作系统是Window7 64位。试验数据采用某区域5m分辨率的卫星影像通过密集匹配并滤波后得到的点云数据。点云数据有A、B两块，A区域的数据量为：356MB(文本文件)，含有10989051个点;B区域的数据量为：1.14GB(文本文件)，含有36551055个点。DEM的采样分辨率设置为15m，最邻近点的检索数量设置为4个，距离阈值d设置为60m(即4倍的DEM采样分辨率)。主要统计的指标有最邻近点查询的正确率、空间索引的构建时间以及DEM插值计算时间(邻域点的搜索与插值)。对于栅格法由于不同参数的设定会产生不同的试验结果，这里设定k为栅格大小与DEM分辨率的比率，n为待插值点所在栅格的邻域栅格的范围(n邻域)。

试验二：利用试验一中表现效果较好的空间索引，通过反距离加权插值算法完成A区域的DEM的采样，并通过目视评估采样效果。

3.2 试验分析与结论

试验一的结果见表1。

表1 不同空间索引的统计指标

通过表中的指标统计，可以看出，点云数量和插值点数的比例并非理论上的9∶1(DEM分辨率和影像分辨率的比例为3∶1)，这是因为实际插值的范围并非恰好是点云数据的平面分布范围，而是矩形包围盒的范围，因此，插值点的数量会比理论上要多。对于栅格法，空间索引的构建时间与点云数量成正比，与栅格的大小没有关系，而插值的计算时间与检索的邻域范围成正相关关系，与插值点数成正比。当k=2、n=8时，正如前述的分析的那样，并不能保证最邻近点检索的正确性，而对于k=2、n=24和k=4、n=8的情况，试验结果与理论相符(与距离阈值d的设定有关)，能保证最邻近点检索的完全正确。对于KD树，空间索引构建时间与点云的数量成正比，插值计算时间与插值点数成正比，并且KD树能保证检索的最邻近点完全正确。对比两种空间索引，在保证正确率的前提下，可以得出的结论是KD的效率要优于栅格法。

根据上述结论这里选取KD树作为空间索引进行试验二。试验二的结果如图4所示。

图4 DEM采样效果

图4中左上角为原始点云，左下角为采样后的DEM，右侧分别为原始点云和采样后DEM的局部放大图，从图中可以看出基于KD树的DEM插值的效果较为理想。

4 结 语

本文对DEM插值中常用的空间索引进行了详细的介绍和分析，指出了其中存在的问题，并在此基础上引入了KD树。试验证明，KD树在效率方面具有优势，并且基于KD树的DEM插值的效果很好。当然栅格法的特点是实现简单、灵活，对于不同的数据特点、参数设置和成果要求，栅格法同样可以加以运用。

[1]张亚南.DEM分辨率确定与尺度转换方法研究[D].南京：南京师范大学，2014.

[2]张海霞，陈向阳，赵文普等.高分辨率遥感影像自动生成DEM的研究[J].测绘与空间地理信息，2015(7)：103-105.

[3]汤国安.我国数字高程模型与数字地形分析研究进展[J].地理学报，2014，69(9)：1305-1325.

[4]张锦明.DEM插值算法适应性研究[D].郑州：信息工程大学，2012.

[5]王耀革.DEM建模与不确定性分析[D].郑州：信息工程大学，2009.

[6]卢华兴，刘学军，汤国安.DEM误差模型研究[C].郑州：第三届地理信息系统全国博士生学术论坛，2008.

[7]李新，程国栋，卢玲.空间内插方法比较[J].地球科学进展，2000，15(3)：260-265.

[8]Bentley JL.Multidimensional Binary Search Trees Used for Associative Searching[J].Communications of the ACM，1975，18(9)：509-517.

[9]Muja M，Lowe D G.Scalable Nearest Neighbor Algorithms for High Dimensional Data[J].IEEE Transactions on Pattern Analysis&Machine Intelligence，2014，36(11)：2227-2240.