基于自抗扰控制的车载发电系统研究

陈路明，廖自力，刘春光

(陆军装甲兵学院，北京 100072)(9)

0 引 言

随着工业技术的不断发展，车载用电设备种类和数量的不断增多，车辆电能需求呈现显著增长态势。传统车辆多以机械传动方式为主，其发电系统逐渐难以满足车辆的电能需求。为突破的结构性发展瓶颈，研究者将目光转向电传动车辆方向。电传动车辆以电能作为内部动力传递方式，具有布置的灵活性和传递的高效性，因此成为应对电气化挑战的重要手段[1]。车载发电系统是电传动车辆的核心动力系统，通过发动机带动发电机旋转进行发电，完成机电能量之间的转化，配合高功率密度或能量密度的储能装置，稳定输出高质量电能[2]。考虑到车辆运行环境通常比较恶劣，存在诸多不确定性的扰动影响，如转矩脉振、转速波动和负载突加突卸等，可能造成系统工作的不稳定性，制约其在大功率电传动系统中的应用。

为攻克这一问题，国内外学者进行了很多尝试，提出了很多抑制扰动的方法。总结起来大致可以分成硬件方面改变系统自身结构和软件方面改进系统控制方法两种。改变系统固有结构是指对明显影响电机性能的电机结构进行优化设计，如转子磁极倾斜或者定子斜槽等[3]，受到当前电机工艺水平等条件限制，电机自身结构改进空间已接近极限；改进系统控制方法是指对通过有效控制以减少扰动影响的方法，车载发电系统大多基于常规PID 控制方式设计[4]，主要面向线性控制系统，但距离非线性系统稳压发电要求还存在一定差距。先进的计算机控制技术为系统的实时状态计算或状态估计提供了应用空间，并且为模糊控制、神经网络控制和自适应控制等智能方法的应用提供了可能[5]，有助于提升车载发电系统的稳压输出能力。

自抗扰控制(以下简称ADRC)继承了常规PID控制器不依赖对象模型的优点，是与现代控制理论相结合发展起来的新型非线性控制技术，从根本上克服了常规PID的结构性缺陷，自动检测和补偿内外扰动，因此具有良好的控制效果[6-7]。在工程实践上，ADRC技术在电气系统、化工过程和精密机械等领域得到广泛应用。本文以某型军用电传动车辆的发电系统为研究对象，将ADRC引入到车载发电系统结构中，以提高系统在扰动下的稳压发电性能。

1 车载发电系统概述

1.1 系统结构

车载发电系统由发动机、永磁同步电机、整流功率变换器、储能元件(主要为动力电池和超级电容复合电源)、控制器和转子位置检测器等构成[8]，其结构如图1所示。

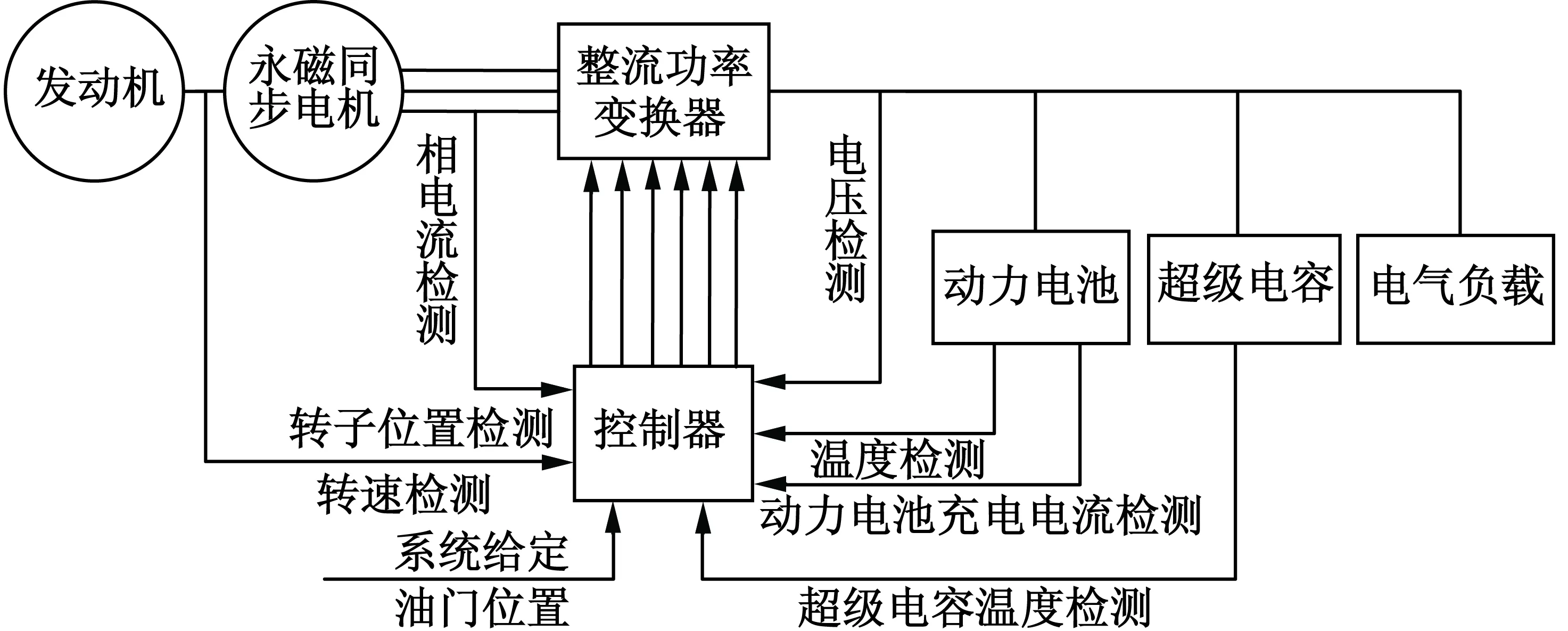
图1 系统结构示意图

图1中各部件功能如下：控制器对来自永磁同步电机、发动机、动力电池和超级电容等部件的信号进行处理，输出控制指令给功率变换器，控制电机工作状态；内置式旋转变压器检测转子位置和转速信号，将检测结果输送给控制器；整流/逆变功率变换器处理来自控制器的信号，完成交流电到直流电整流变换及其可逆变换过程；储能元件由超级电容和动力电池组成，不同部件特性优势互补，用于满足负载的功率和能量需求。

1.2 电机数学模型

在d-q坐标系下建立永磁同步电机数学模型，从定子电压、定子磁链、电磁转矩和机械运动运动方程4个角度进行描述[9]，分别表示:

定子电压方程:

(1)

定子磁链方程:

(2)

电磁转矩方程:

(3)

机械运动方程:

(4)

式中：ud,uq为定子d,q轴电压；Rs为定子相电阻；id,iq为定子d,q轴电流；p=d/dt为微分算子；ψd,ψq为定子d,q轴磁链；ωe为转子旋转的电角速度；Ls为定子电感；p为极对数；ψf为永磁体磁链；Te为电磁转矩；TL为负载转矩；J为转动惯量；ωm为电机转子的机械角速度；B为粘滞摩擦系数。

1.3 发电控制策略

车载发电系统通常采用电压外环、电流内环的结构，考虑外环反馈特性，控制电机输出电压恒定，将给定电压与反馈电压的差值作为控制量，控制车载发电系统，原理如图2所示。

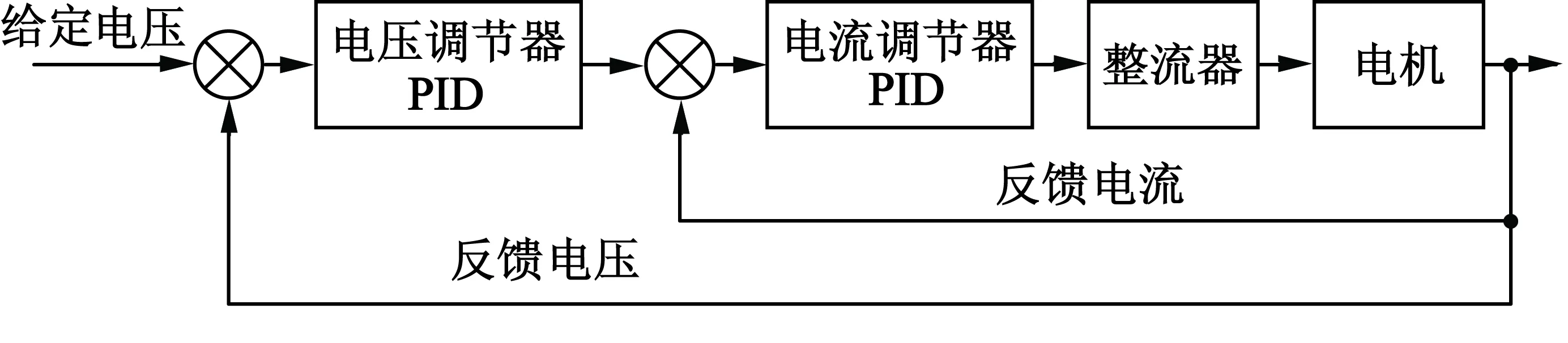
图2 车载发电系统控制原理示意图

发电阶段电机转速通常高于额定转速，为保证电机仍运行在恒功率状态，需要采取弱磁方式进行磁场校正，考虑到逆变器额定电压和容量限制，电机最大相电流幅值ismax和最大相电压幅值usmax存在以下约束条件[10]:

(5)

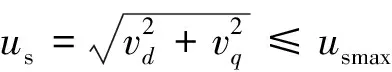
(6)

由式(5)知，电流约束关系在iq-id坐标平面面上构成一个圆，由下式可得:

(7)

由式(6)知，电压约束条件在iq-id坐标平面上构成一个椭圆，由下式可得:

(8)

电流极限圆和电压约束椭圆如图3所示。

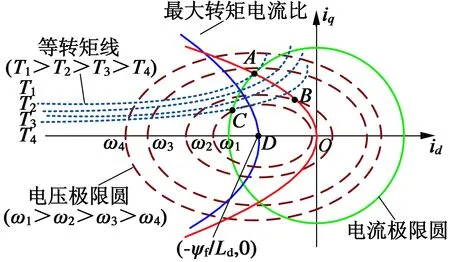
图3 弱磁控制中iq-id变化关系图

由图3可知：电压约束椭圆以(-ψf/Ld,0)为中心，并随转速升高而减小；当电机转速继续升高时，电机反电势将不断增大；当电机转速达到ω4时，即p·ω4·ψs=usmax时，此时电机反电势达到逆变器最大限制电压；当电机转速增大到ω≥ω4时，电机进入恒功率运行状态，弱磁控制直轴电流id和交轴电流iq大小，使电机转速进一步增加。

2 ADRC设计

为发扬常规PID控制器的优点，克服其不足，中科院韩京清研究员提出了一种自抗扰的鲁棒性控制技术，该方法深度结合了现代控制理论非线性的控制特点，不需知道被控对象具体模型，通过自动计算并补偿未知扰动，提高控制性能。

2.1 自抗扰控制器结构

图4为ARDC的结构框图。它主要包括3部分组成[11]：扩张状态观测器(以下简称TD)、跟踪微分器(以下简称ESO)以及非线性状态误差反馈控制律(以下简称NLSEF)。假设受到未知扰动作用的非线性不确定对象数学模型:

(9)

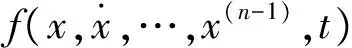
其中，ESO作为ARDC的核心，用于观测系统状态，实时补偿系统总扰动；TD用于快速无超调的跟踪系统输入，给出其各阶微分信号；NLSEF用于对输入信号进行非线性组合，生成补偿控制量。

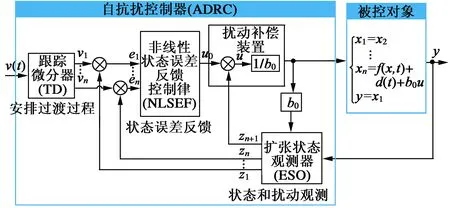
图4 ADRC结构框图

2.2 ADRC数学模型

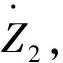
TD:

(10)

ESO:

(11)

NLSEF:

(12)

式中：e为系统输出量与输出值之间差值；z1，z2分别为系统输出量及其微分估计值；β1,β2为表达式的可调参数，需要被整定；α1,α2为滤波因子；δ为线性区间的宽度；b为扰动补偿参数；u为补偿后得到的控制量；v1为输入信号的跟踪值；v为输入信号的给定值；r为速度因子，决定跟踪的速度；h为滤波因子，对噪声起滤波作用；e1为输入信号的跟踪值与输出值之间差值；u0为非线性组合输出的控制量；α为滤波因子。

非线性滤波函数fal(·)取:

(13)

由于ADRC结构中包含较多参数，需要依据已知的被控对象特点等信息，整定内部参数，建立面向对象的ADRC应用模型。

2.3 ADRC仿真模型

依据数学模型，在MATLAB/Simulink仿真环境中搭建ADRC模型[13]，如图5所示。

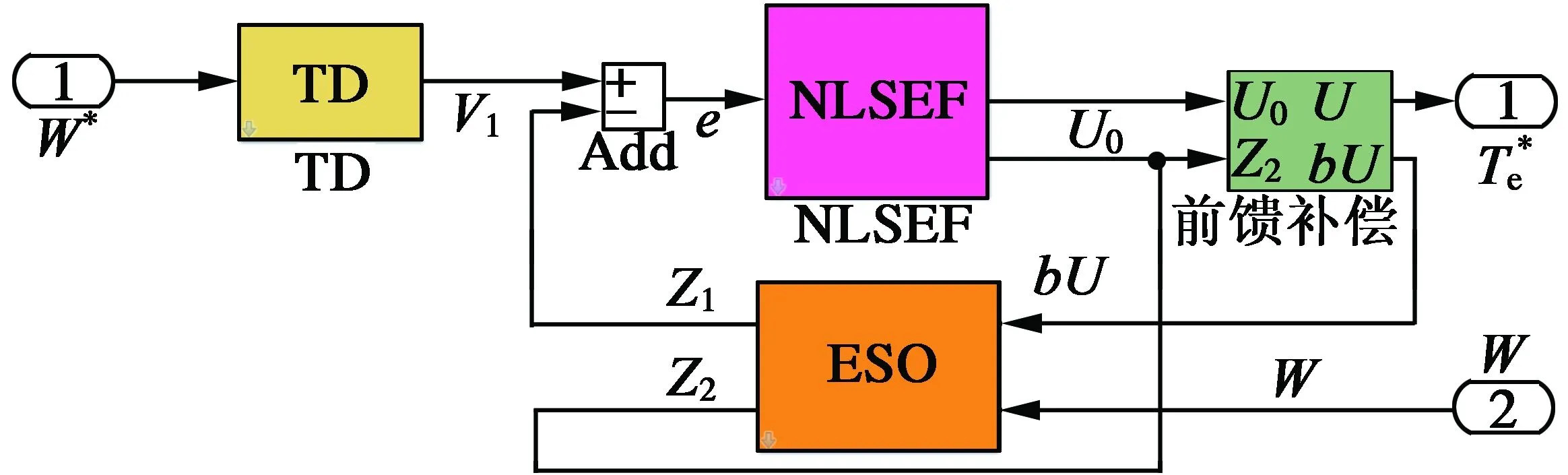
图5 MATLAB/Simulink ADRC仿真模型

ADRC各主要部分的仿真模型如图6所示。

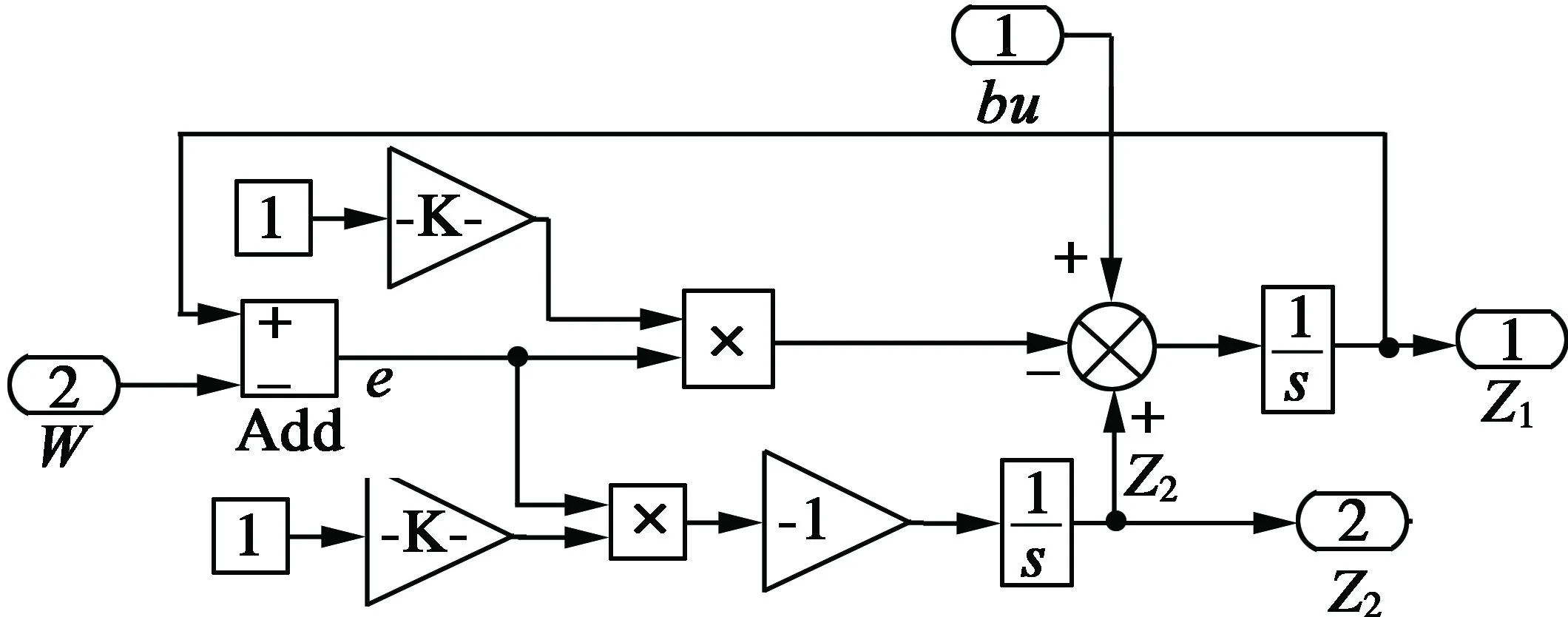
(a) TD

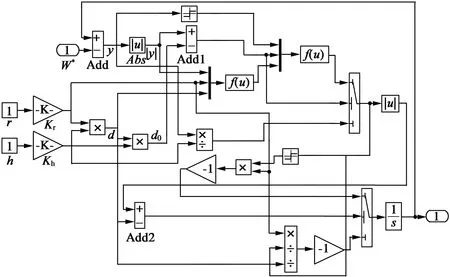
(b) ESO

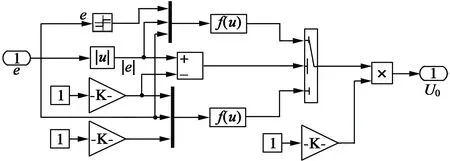
(c) NLSEF

将上述结构进行封装，得到ADRC功能模块，替换常规PID控制器，嵌入到车载发电系统模型，图7即为建立得到的自抗扰发电系统模型。

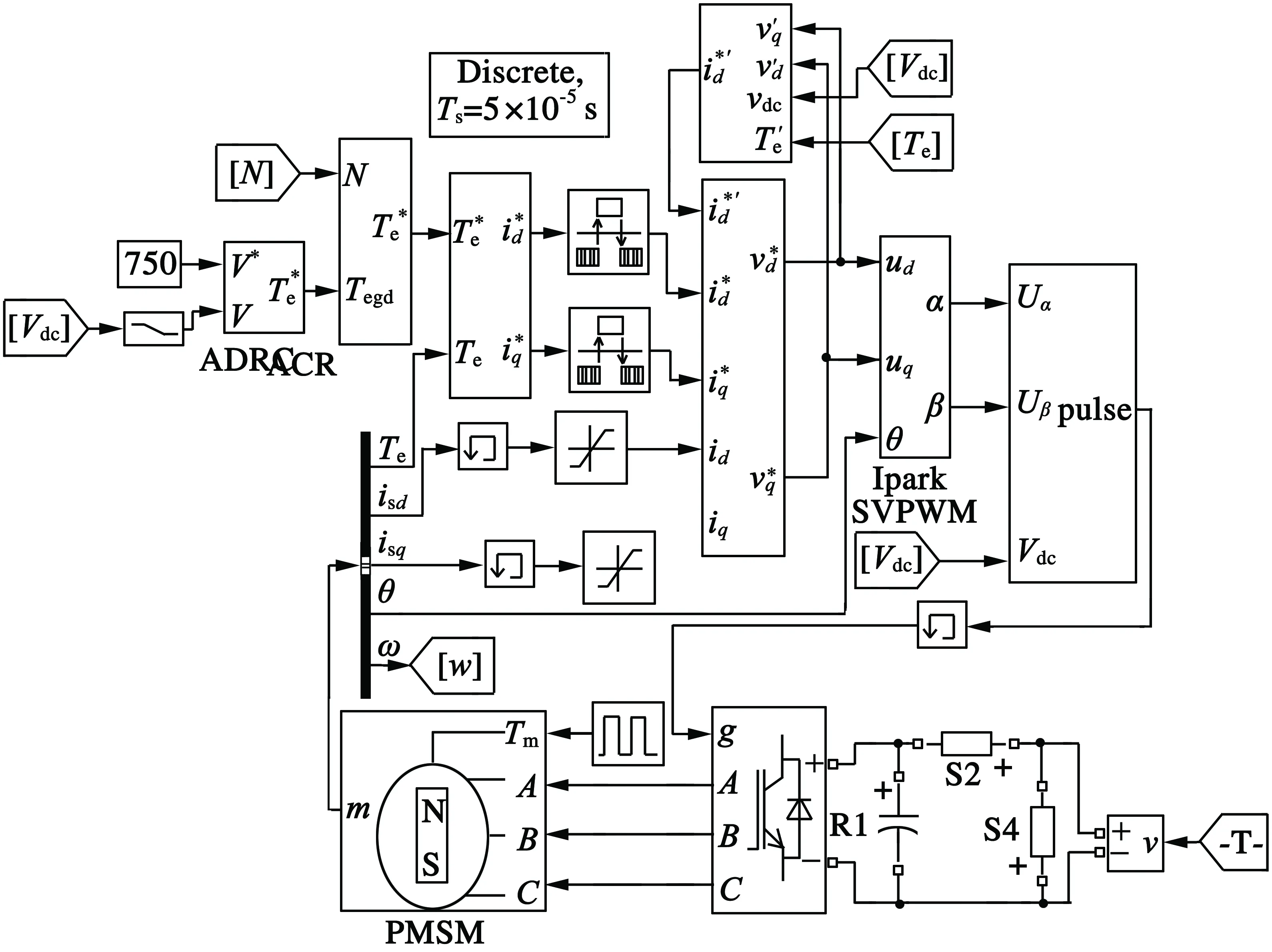
图7 基于自抗扰的车载发电系统模型

3 仿真试验结果

仿真试验前，需要对车载发电系统模型进行参数整定：首先依据表1所示的永磁同步电机主要参数，建立实际电机仿真模型；然后整定控制器主要参数，建立自抗扰发电系统模型的应用基础；最后设定扰动环境，观测输出结果，对比研究两种控制器的作用效果。

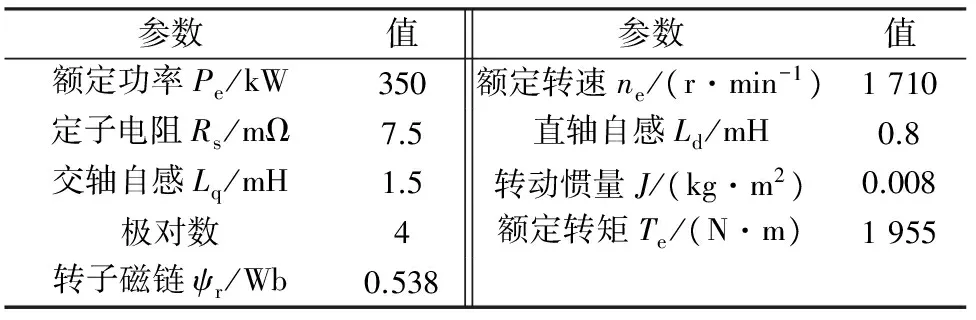
表1 永磁同步电机主要参数

根据实际调节经验，对基本参数进行整定：TD中速度因子r尽量较大，取为r=100，兼顾滤波效果和安排过渡过程，设定滤波因子h=0.1；取滤波函数fal(·)中的各参数为α1=05，α2=0.25,δ=0.05，扰动补偿参数b=1.5npψf(JLq)-1作为参考值，β1=120，β2=2 500；取NLSEF中α=0.1，β=80，建立起ADRC仿真模型。

为检验基于自抗扰控制的车载发电系统效果，将外部扰动下的主要参数变化作为参考指标，采用有限带宽的白噪声模拟发动机油泵故障或积碳等造成的转速扰动，对比研究ADRC和常规PID控制器的输出曲线，结果如图8所示。

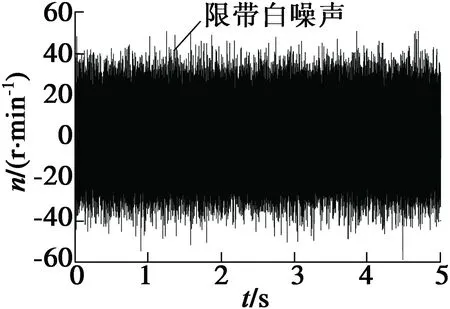
(a)转速波动噪声曲线

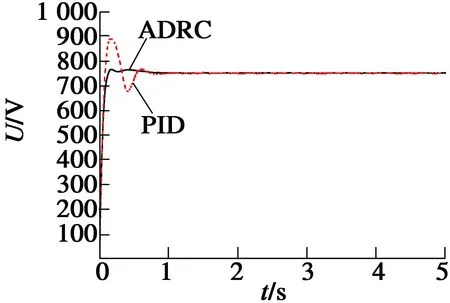
(b)输出电压变化曲线

(c)输出电压局部放大曲线

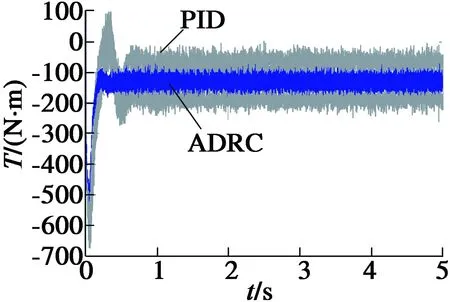
(d)电机转矩变化曲线

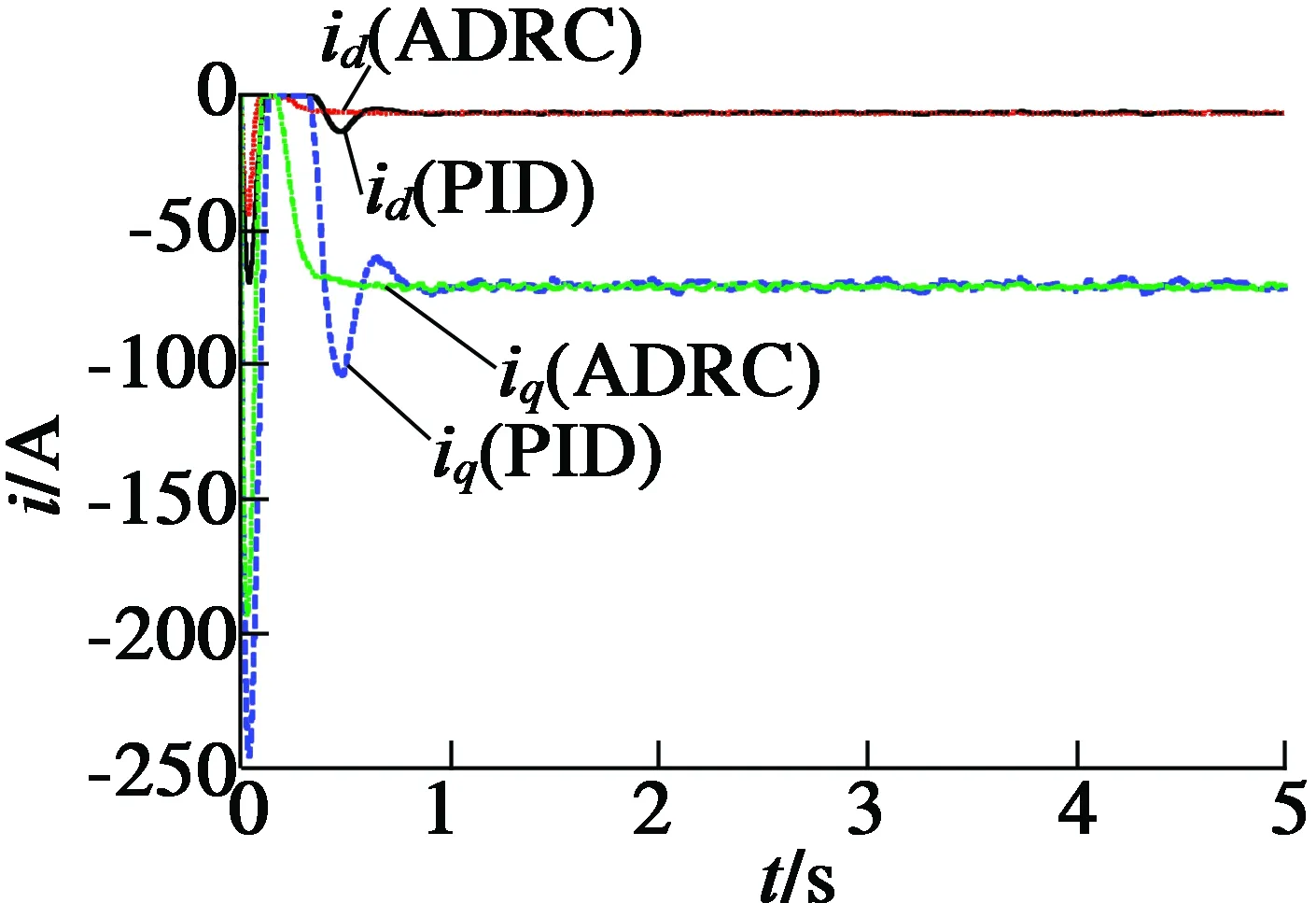
(e)电机电流变化曲线

由图8可知，车载发电系统采用不同的控制器得到的结果存在一定差异。开始时，常规PID控制器电压曲线上升迅速，但出现明显超调，0.6 s左右输出电压能够稳定在750 V左右，相比而言，ADRC电压曲线上升较慢，但基本不超调，0.3 s左右输出电压稳定在750 V左右；在1 s时刻后，由于转速存在噪声扰动，转速在50 r/min上下波动，导致输出电压的不稳定，ADRC电压波动在1 V左右，明显小于常规PID控制器近4 V的电压波动，对扰动的抑制作用比较显著。

另外，采用ADRC后，车载发电系统的转矩波动幅值得到降低，明显低于常规PID控制器的对应结果；在施加转速噪声扰动时，能够通过内部补偿机制快速抑制扰动影响。同时，ADRC电流波动的幅值和频率得到改善，明显低于常规PID控制器的对应结果。总之，相比常规PID控制的车载发电系统，自抗扰控制的车载发电系统稳压控制效果得到显著提升。

4 结 语

针对车载发电系统存在的扰动问题，建立了永磁同步电机数学模型和车载发电系统仿真模型，引入自抗扰控制手段研究转速扰动下的系统输出变化情况，对比常规PID控制器的仿真结果，验证了自抗扰控制在车载发电系统中应用的可行性。然而，在控制器设计过程中，主要侧重外部扰动对系统的影响，还未将内部的诸多扰动因素考虑进来，后续研究中要侧重研究内部主要的扰动因素，优化调整ADRC自身结构和控制参数，全面提升车载发电系统的稳定工作能力。

[1] 廖自力,马晓军,臧克茂,等.全电战斗车辆发展概况及关键技术[J].火力与指挥控制,2008,33(5):1-4.

[2] 张希,米春亭.车辆能量管理:建模、控制与优化[M].北京:机械工业出版社,2013:127-138.

[3] 夏长亮,俞卫,李志强.永磁无刷电机转矩波动的自抗扰控制[J].中国电机工程学报,2006,26(24):137-142.

[4] 卢铁军.混合动力汽车电动机/发动机一体化控制系统研究[D].北京:北京信息科技大学,2013.

[5] 卢达.永磁同步电机调速系统控制策略研究[D].杭州:浙江大学,2013.

[6] 邱晓波,窦丽华,韩京清,等.自抗扰控制在坦克机动目标状态估计中的应用[J].兵工学报,2009,30(7):104-107.

[7] 郭鑫,刘新妹.自抗扰控制器在平面电机控制系统中的应用[J].计算机测量与控制,2014,30(7):989-993.

[8] 毛明,韩政达,刘翼.论全电车辆的能量管理和功率管理[C]//第三届特种车辆全电化技术发展论坛组织委员会.第三届特种车辆全电化技术发展论坛论文集,2014:162-168.

[9] 刘伟,殷国栋.混合动力汽车系统建模与控制[M].北京:机械工业出版社,2014:28-31.

[10] 唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,2010:252-262.

[11] 郑颖,马大为,姚建勇,等.基于自抗扰技术的火箭炮伺服系统解耦控制[J].火炮发射与控制学报,2014,35(4):6-10.

[12] 苏位峰.异步电机自抗扰矢量控制调速系统[D].北京:清华大学,2004.

[13] 王正林,王胜开,陈国顺,等.MATLAB/Simulink与控制系统仿真[M].北京:电子工业出版社,2012:44-64.