水下仿生机器人CPG控制方法研究现状综述

闫勇程，王扬威，兰博文，赵东标

(南京航空航天大学，南京 210016)

0 引 言

进入21世纪以来，海洋资源的战略地位越来越重要，人类也不断加快了探索海洋的步伐，各类水下机器人应运而生。传统的基于螺旋桨推动的水下机器人应用最为广泛，但是在机动性、功重比、稳定性等方面仍存在较大不足。而鱼类经过长期的遗传进化、自然选择，能够适应时刻变化的水下环境，具有优异的水下运动能力进行各项生命活动。随着人类在生物仿生学、流体力学、计算机软件技术以及智能材料等方面取得的一系列进步，国内外科研人员已成功研制出了多种水下仿生机器人[1]，在鱼类的形体和结构仿生方面已经取得了一系列成果，而在运动控制方法上与生物的神经系统控制还存在较大差距，已成为阻碍水下仿生机器人发展的主要问题。

目前水下仿生机器人常用的运动控制主要有基于模型的控制方法、正弦控制器和基于中枢模式发生器(以下简称CPG)的控制方法。

基于模型的控制方法[2-3]是建立在被控对象的运动学和水动力学模型基础上的一种控制方法，能实现准确的运动控制。但由于水下推进装置的精确建模十分困难，因此目前大都采用简化的数学模型用于控制系统，使得控制系统的鲁棒性不佳，机器人不能很好的适应水下非结构化的工作环境。正弦控制器[4-5]是水下仿生机器人运动控制方法中常用的一种控制方法。因为大多数鱼类的身体或鳍的推进波形接近正弦运动，所以该方法将水下仿生机器人推进器中每个关节的运动规律设定为正弦周期运动，再通过改变不同关节之间运动的相位差来改变运动策略。这种控制方法能明确描述推进波的频率、幅值和相位等参数的关系，且便于计算机编程。但是当控制参数(如频率、幅值)突变时易导致关节角产生不连续的跳变，从而损害关节的驱动电机和传动系统，虽然可以编写专门的过渡函数来克服这种跳变，但是灵活性较差。再者，正弦控制器算法较难引入外部反馈信号，适应性不足。基于CPG的控制方法[1]是通过模仿动物节律运动的生物学控制机理，以CPG神经元网络数学模型作为底层的运动控制器，产生连续协调的节律运动控制信号，运动控制的协调稳定性和环境自适应性较好。

本文介绍了广泛用于水下仿生机器人的CPG控制方法的原理，结合具体实例分析了CPG控制的关键技术问题。

1 生物CPG控制原理

自然界中动物常见的运动方式是节律运动，如动物的行走、奔跑、跳跃、游泳、飞行以及动物的呼吸、心脏跳动等都是节律运动。在亿万年的自然选择与遗传进化中，动物的节律运动具有了高度的协调性与自适应能力。

生物CPG的研究及发展经历了一个漫长的过程，在20世纪初，关于动物节律行为的产生主要有两种观点：一种观点是以Sherrington为代表的认为感觉反馈发挥着重要作用，节律运动是反射行为在不同运动周期触发连锁反应的结果；另外一种解释则是以Brown[6]为代表的认为节律行为的产生不需要外部的信号输入，如感觉反馈的输入。1914年Brown[7]提出了一个半自主神经振荡模型，在两个群之间加上相互抑制的耦合神经元，并且加入神经元的疲劳机制来产生交变节律性运动。到目前为止，已经有充足的证据表明，节律运动产生是不需要感知系统的信息反馈的。很多相似的实验表明，中央模式发生器是由很多耦合振荡中心组成的分布式网络。七鳃鳗的脊椎大概有100段，它们之中大概只有一到两段能产生节律性的运动。在蝾螈中也可以观察到同样的结果[8]。1961，Wilson[9]发现了中枢模式神经振荡器发生网络，生物CPG的研究取得了重要突破，其后在1980年，Delcomyn[10]又提出CPG是脊椎和无脊椎动物的很多节律性行为的神经基础。1985年，Grillner[11]提出CPG是以一对相互耦合的神经元为基本单元，每一个运动关节或者说自由度至少有一个CPG基本单元。1998年，Cheng[12]等人通过实验提出这些单元能被进一步的划分为屈肌和伸肌的独立振荡中心。尽管感觉反馈对于节律运动的产生不是必要的，但是它却对节律运动的调节有重要作用，对于身体运动的协调性方面有着重要影响。

总结来说，生物CPG的特点有以下3个：

1)在生物体的运动环控制中能够减少时间延迟，因为基本节律运动的产生是通过脊椎的反馈环，而高层神经中心，如运动皮质、小脑与基底神经节会根据环境的不同来调整协调CPG的输出；

2)减少了下行控制信号的维度，因为控制信号不需要指定肌肉的具体活动，而只需要给CPG一个活动信号；

3)减少了高层调节中心与脊椎之间的所需带宽。

2 水下仿生机器人CPG控制振荡模型

目前常用的仿生CPG振荡模型主要有3种：1)Kimura递归神经振荡器；2)Ijspeert七腮鳗型相位振荡器；3)Hopf神经振荡器。

2.1 Kimura递归神经振荡器

1985年，日本九州工业大学的Matsuoka通过对生物神经细胞生理活动的研究，提出Matsuoka神经振荡器模型[13]，该模型将模拟神经元疲劳特性的适应项加入到了漏极积分器的微分方程中。2000年，Kimura对Matsuoka提出的模型进行了改进，改变了其只能输出正值信号的缺陷[14]。

Kimura递归神经振荡器是在Matsuoka振荡器基础上改进而来，该振荡器是使用两个基本的神经元相互抑制形成一个振荡器单元，两个基本的神经元分别对应生物体内屈肌与伸肌运动控制神经元，由一组非线性微分方程描述，如下：

(1)

式中:ui是第i个神经元的内部状态变量；vi是代表第i个神经元的自抑制程度；yi是第i个神经元的输出；u0表示外部常数项输入;表示神经元稳定后输出的幅值；Fi表示外部环境反馈输入；β表示自抑制对神经元自身内部状态的影响程度；τ与τ′分别表示ui与vi的时间常数；wij表示神经元i与j之间的耦合权重。

伸肌神经元的输出与屈肌神经元的输出相减，如图1所示，差值作为神经振荡器的输出，通过这种方法克服了Matsuoka振荡器模型只输出正值信号的不足，如式(1)所示。

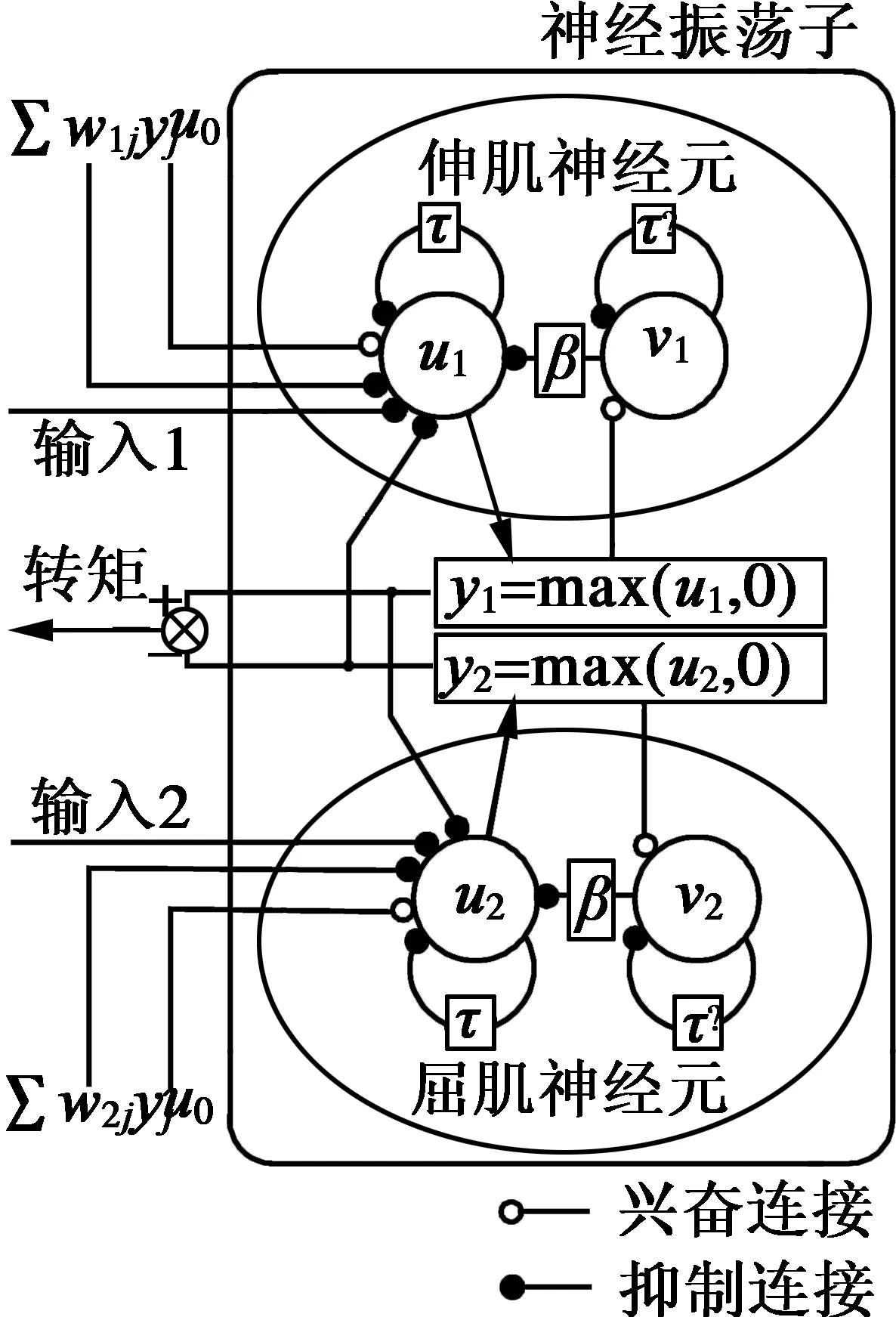
图1 Kimura递归神经振荡器

Kimura递归神经振荡器的优点在于：1)用简单的数学表达式将运动神经元的生物学特性表示出来；2)引入外部环境反馈项可以改善机器人的运动协调稳定性与环境自适应能力；3)CPG控制模型具有一定的通用性，可以产生不同的节律性控制信号，即不同的运动步态，用于不同类型的机器人。

水下仿生机器人的每个关节的输出可以由一个Kimura递归神经振荡器进行控制，振荡器的输出作为机器人关节的目标角度，通过设计合理的振荡器网络拓扑结构及合理的耦合关系和连接权重，可协调机器人各个关节的运动，产生不同的游动步态。

王龙[15]等人采用4个Kimura振荡器构建了CPG网络模型，用来控制仿生机器鱼的具有两个自由度的胸鳍及尾鳍，如图2所示，并且引入了头尾轴与水平面的夹角以及偏航角作为反馈信息控制机器鱼的游动姿态，对胸鳍的运动控制做了深入探讨，在Walker的摆动胸鳍模型基础之上制定了基本的游动策略。仿真实验结果表明，此CPG模型能实现机器鱼的俯仰与转弯运动，并能根据反馈的信息快速调节CPG网络的输出。

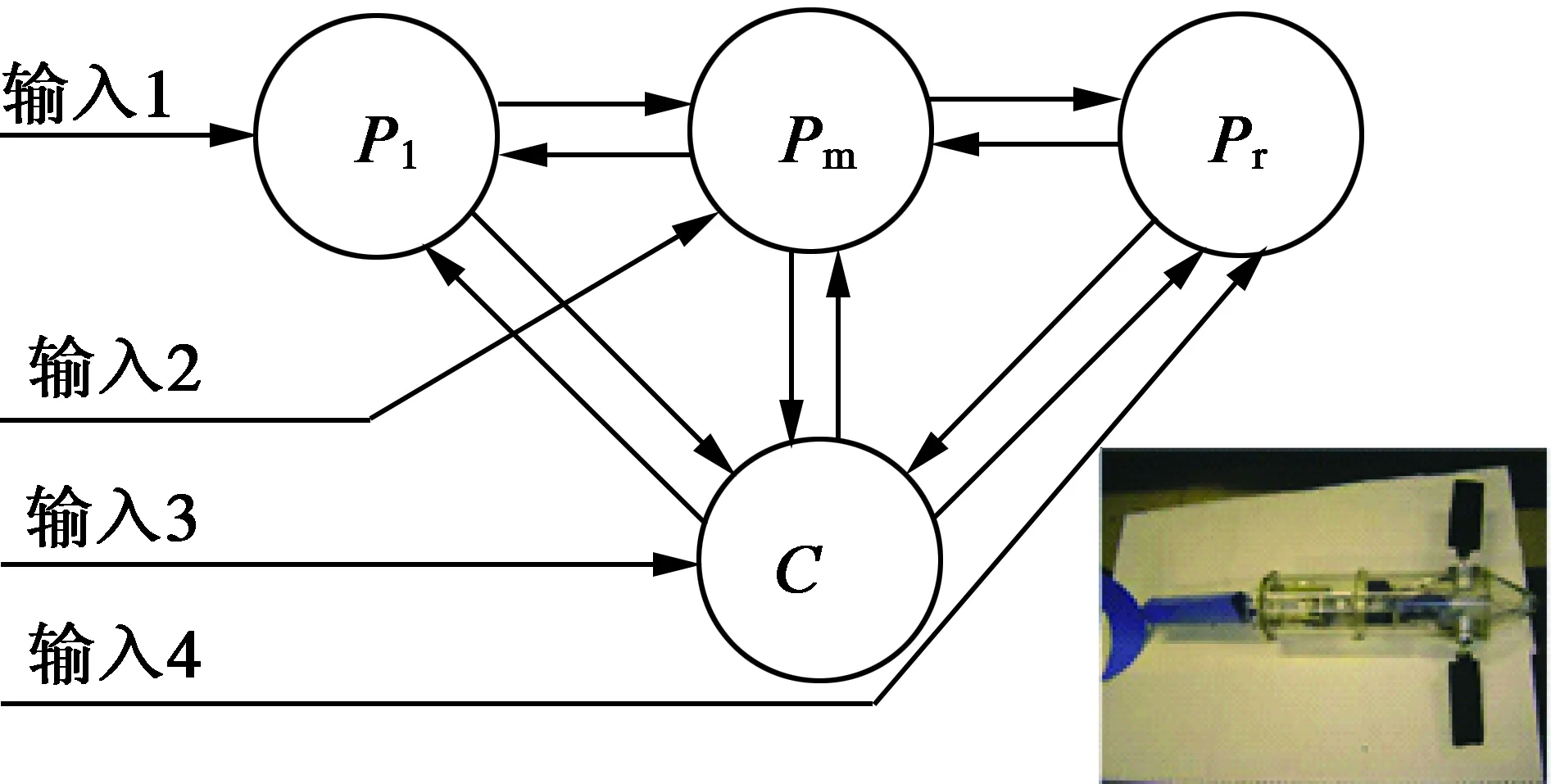
图2 CPG网络拓扑结构与机器鱼样机[15]

Tangorra[16]等人以蓝鳃太阳鱼为仿生对象，设计了如图3所示的多鳍机器鱼。该机器鱼的推进机构由7个可变形的仿生鳍构成，仿生鳍上及鱼体两侧含有分布式压力传感器，可用来感知水动力流场，并且含有模仿鱼类前庭系统的姿态传感器。所构建的CPG网络由4个神经元构成，能够有效实现仿生机器鱼的低速下稳定游动，并且通过试验分析了鳍面上所承受的水动压力与拍动频率的关系，为进一步更精确的利用分布式反馈感知系统结合CPG控制方法做了初步探索。

图3 仿太阳鱼水下机器人[16]

Jeong[17]等人提出了基于粒子群算法(PSO)的CPG控制系统，用于Fibo水下机器人上，如图4所示。一般CPG的参数都是人工根据经验结合计算机数值仿真确定CPG网络中各参数，该方法在人为给定机器鱼的行波参数后，根据Lighthill鱼体波方程，通过PSO算法选取最优的CPG连接权重、自抑制系数及时间常数等共19个参数，仿真及实验展示了此方法的有效性。

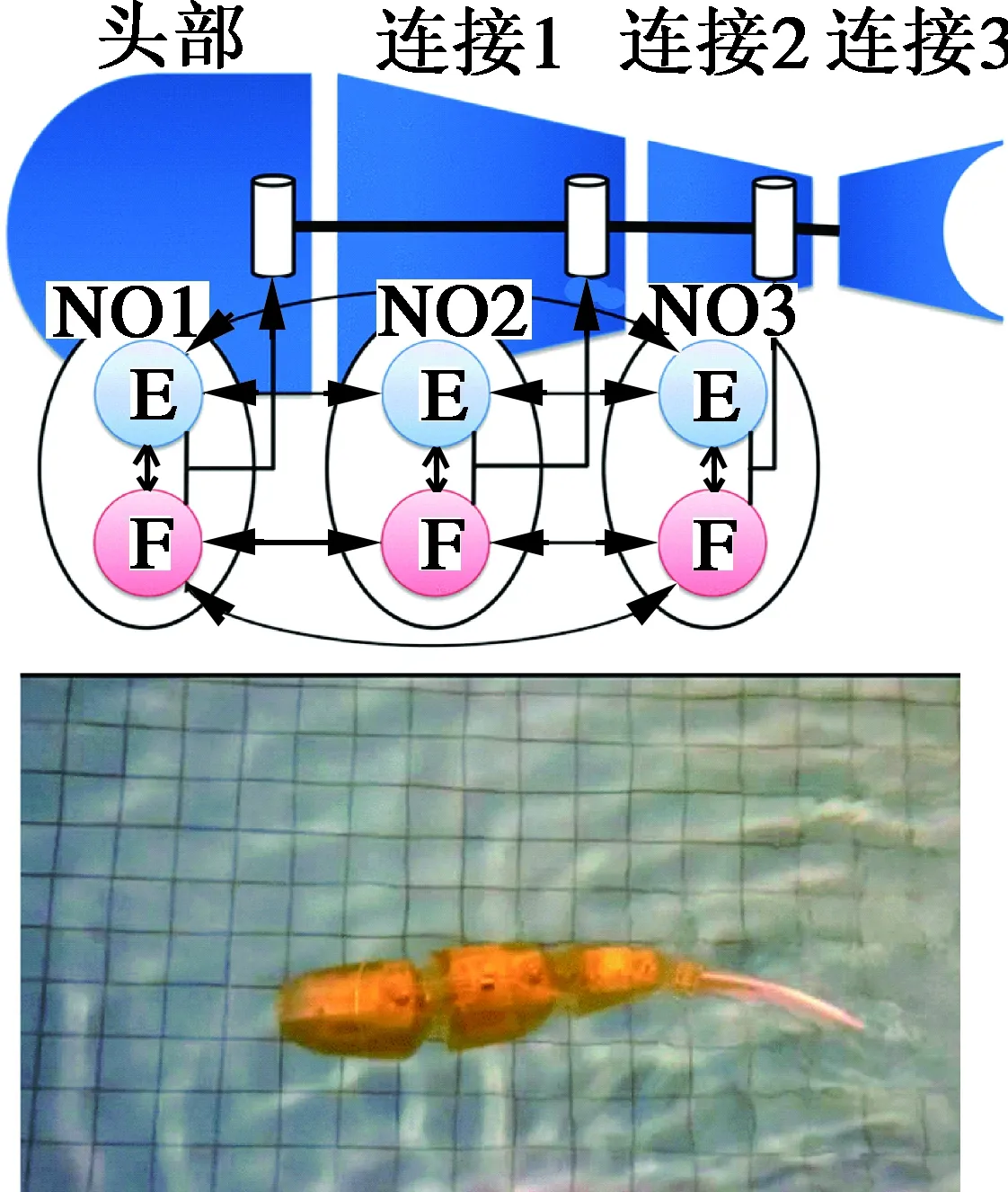
图4 Fibo水下机器人[17]

Ikeda[18]等人采用此振荡器构成的CPG控制网络用于多关节仿蝠鲼机器人的控制，如图5所示，该机器人主要有12根鳍条致动单元，与仿生鳍膜构成双侧波动推进机构，CPG控制网络可以产生节律关节角控制信号，并能实现机器人的偏航机动动作，仿真试验证明了控制系统的可行性与有效性。

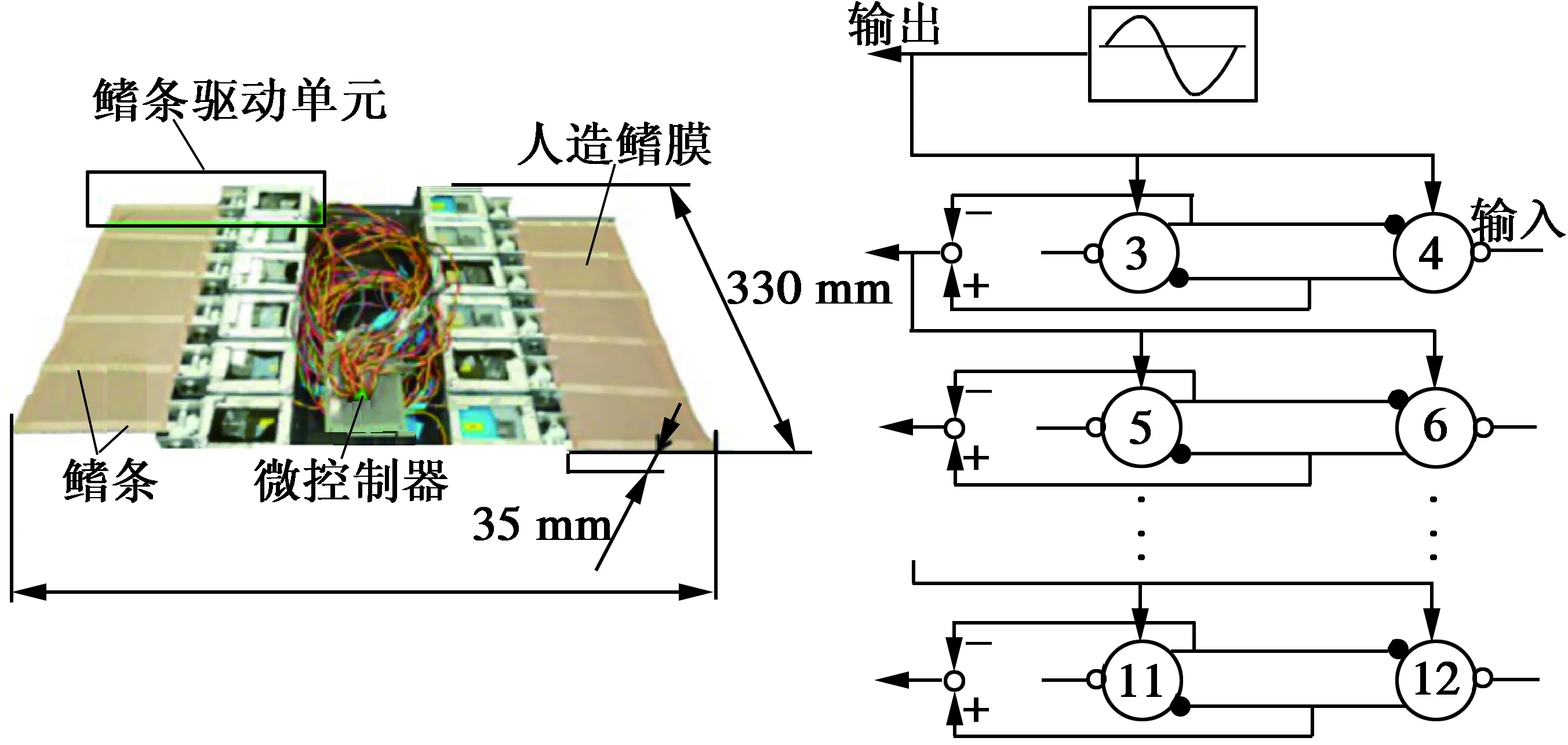
图5 仿蝠鲼机器人[18]

2.2 Ijspeert七腮鳗型相位振荡器

Ijspeert七腮鳗型相位振荡器由瑞士洛桑联邦理工学院科学家Ijspeert提出[19]。根据蝾螈前进中身体行波的特性，提出了比Cohen相位振荡器更简单易用的振荡器模型，如下:

(2)

式中：θi,ri表示第i个振荡器的输出相位与幅值的状态变量；vi第i个振荡器的固有频率；Ri表示固有幅值，即最终ri的收敛值；αi表示幅值ri收敛于Ri的速度；wij表示振荡器i,j之间的耦合权重，反映了振荡子j对i的影响大小；φij表示振荡器i,j之间的相位关系；xi表示第i个振荡器的最终输出。该振荡器能清楚地表达用于控制对象的振幅、频率和相位滞后等参数，具有显式的输出函数，数学结构简单，状态变量少，易于微控制器编程实现。Ijspeert[19]等人成功将此应用于仿蝾螈两栖机器人，该机器人采用20个振荡子，采用如图6所示的拓扑结构，整个控制系统只有一个输入参数d，通过改变输入参数d的大小，能改变机器人在水中的游速及方向，以及切换运动模式，在陆地上也能实现爬行。

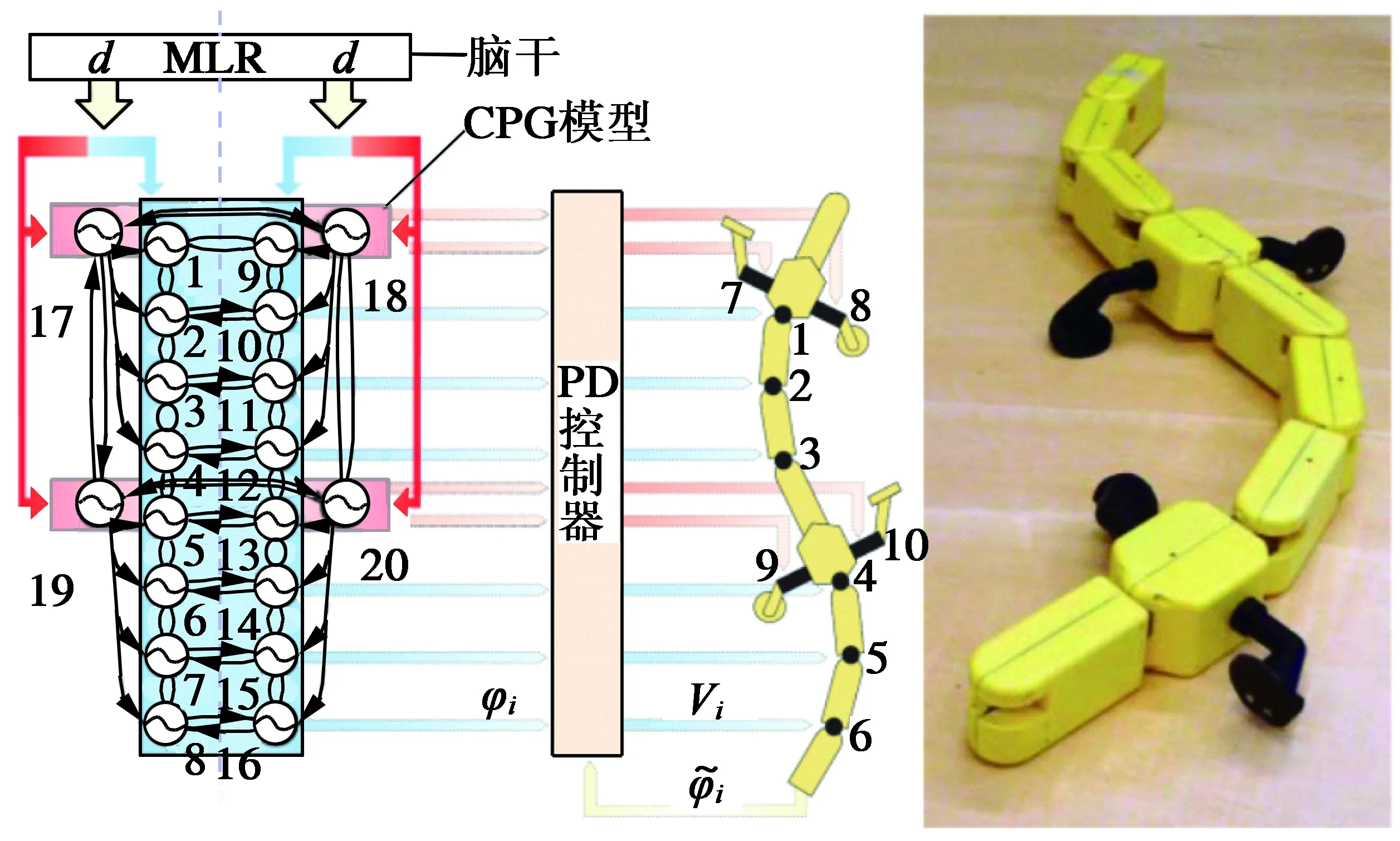
图6 仿蝾螈两栖机器人[19]

Crespi[20]等人又成功利用相同的振荡器，采用3个振荡子相邻耦合的拓扑结构，如图7所示。控制机器鱼Boxybot的一对胸鳍关节及尾鳍关节，通过胸鳍关节配合尾鳍关节的运动，可以实现机器人水下多样的游动步态，实验结果表明这种控制方法能够实现Boxybot水下机器人的趋光性稳定游动。

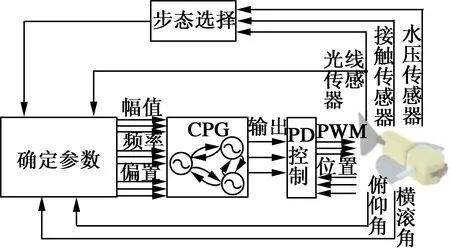
图7 Boxybot水下机器人[20]

Cao[21]等人利用此振荡器构成的CPG网络用于仿牛鼻鲼水下机器人Robo-Ray的机动控制，如图8所示。根据仿生原型牛鼻鲼的形态学与运动学特征，该机器人的机动执行机构主要由对称胸鳍及尾鳍构成，对称胸鳍通过拍动方式提供推力，尾鳍用于俯仰控制，实验证明了此CPG控制模型可以实现多关节牛鼻鲼的直线巡游、偏航、俯仰及速度控制，而且不同游动步态之间切换较平滑。

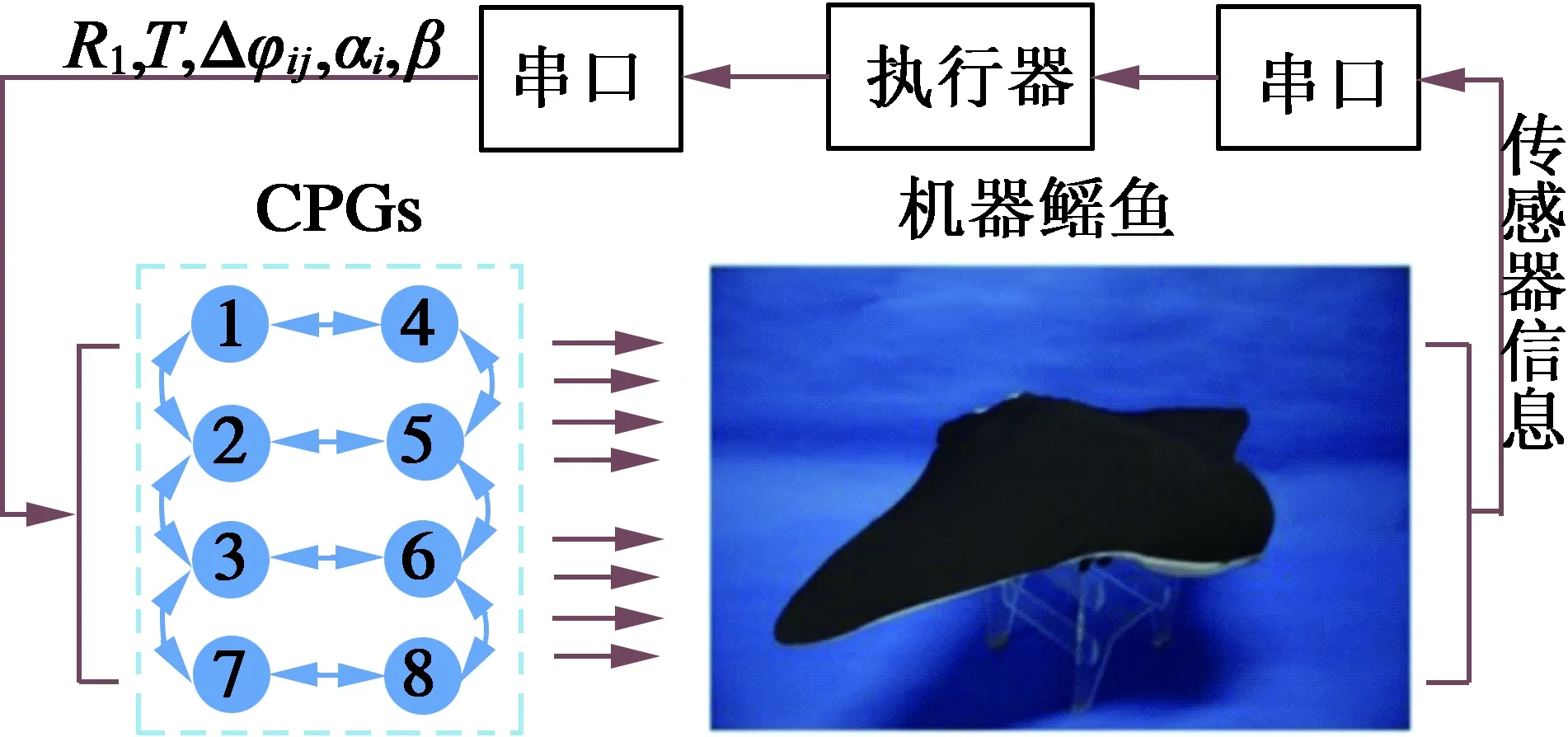
图8 牛鼻鲼水下仿生机器人Robo-Ray[21]

Yu[22]等人在建立了仿鲹科多关节尾鳍机器鱼的拉格朗日动力学模型基础之上，构建了CPG控制模型，被控对象带有一对仿生胸鳍及一个多关节尾鳍，如图9所示。数值仿真及样机实验结果表明了所构建的控制模型的有效性与可行性，并对推进力及游动轨迹进行了理论与试验对比分析。此外还实现了仿生机器鱼的倒游，为鲹科模式推进的机器鱼提供了一种可行的控制方案。

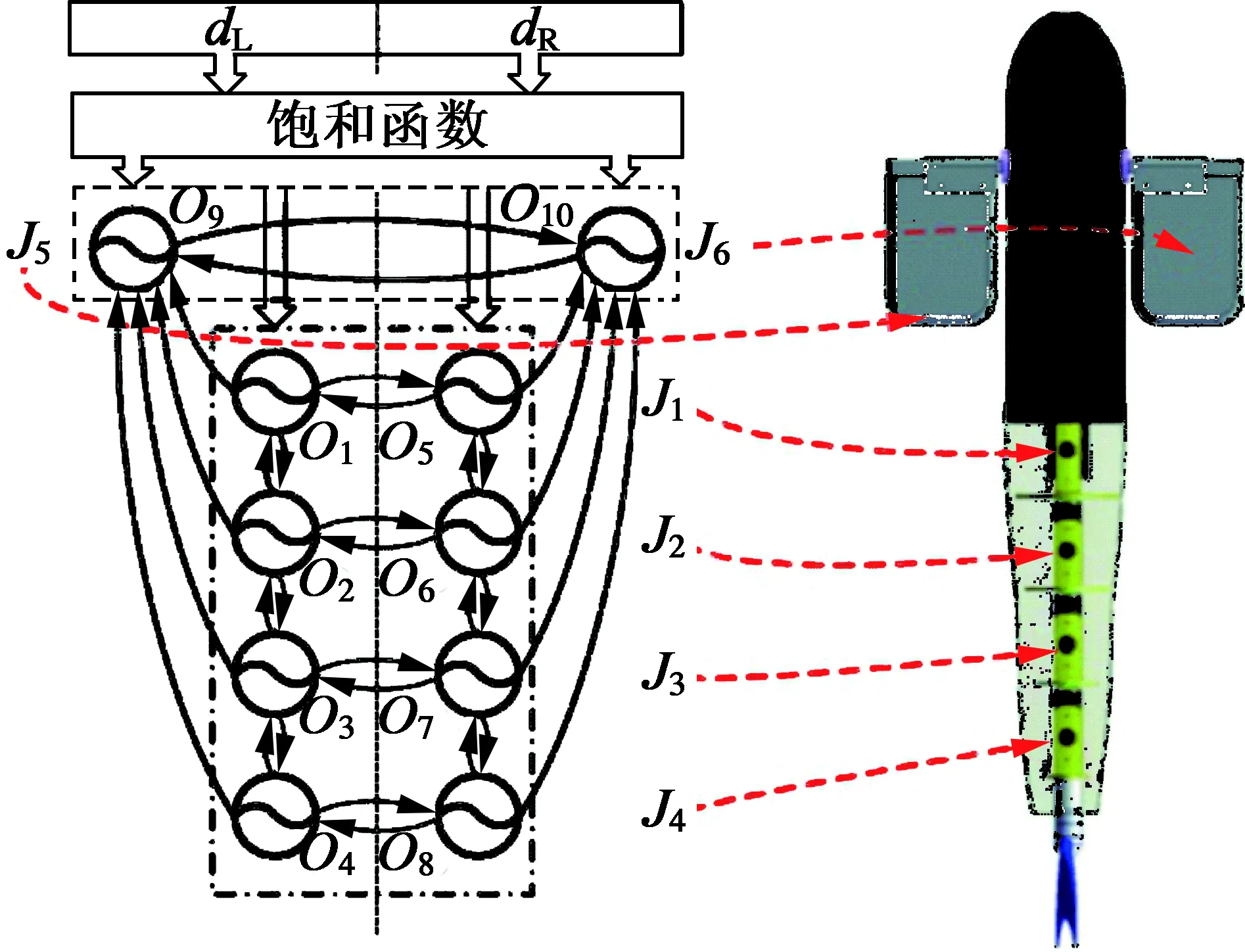
图9 仿生多关节机器鱼[22]

2.3 Hopf神经振荡器

Hopf神经振荡器是指在具有稳定极限环的非线性Hopf振荡方程基础上改变发展而来，无论初始状态如何，振荡器最终会趋于稳定状态。Hopf振荡方程定义如下：

(3)

式中:x与y为状态变量；μ为振荡的幅值；w为振荡的频率；α为正常数，决定收敛到极限环的速度。状态变量x,y最终会收敛于以μ为半径的稳定极限环。

汪明[23]等基于Hopf振荡器提出一种CPG振荡模型，并分析了其数学特性，通过最近相邻耦合的方法，对n个这样的神经元振荡子进行耦合，构建了仿生机器鱼的CPG拓扑网络控制结构，如图10所示，并在建立了胸鳍推进的动力学模型基础之上将其用于机器鱼的控制。导出了机器人直游、倒游、胸鳍-尾鳍协调运动等多种控制策略，还分析了直游、倒游的游速与频率的关系，还探讨了身体-尾鳍推进与身体-尾鳍-胸鳍联合协调推进速度与频率的关系。实验结果验证了此CPG模型的可行性与灵活性，还可用于其他多相似的多关节自由度机器人的控制上。

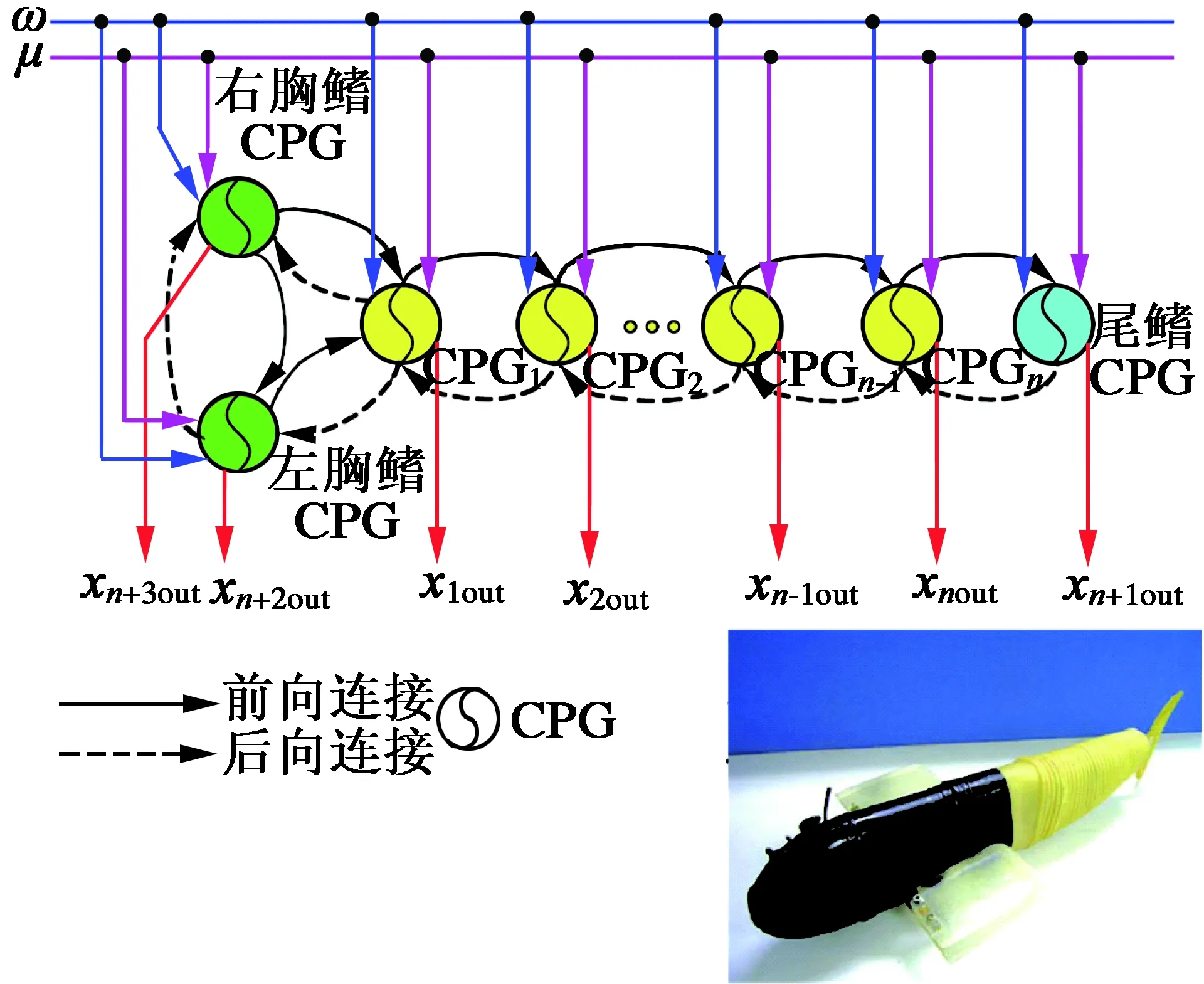
图10 胸鳍驱动型机器鱼[23]

Wu[24]等人以白斑狗鱼为仿生原型设计了经过优化改进的多关节仿生机器鱼，如图11所示。该机器鱼具有流线型的身体,可以实现偏航操作的头部、一对共有4个自由度的胸鳍以及性能更高的处理器和更高力矩的伺服舵机。该机器鱼的控制系统由8个Hopf振荡器构成，整个CPG振荡器按功能可分为3类，即胸鳍CPG、身体CPG及尾鳍CPG，分别控制机器鱼的胸鳍、身体及尾鳍。此CPG拓扑网络能够实现多种游动模式，如直线前向游动、向后游动、转弯、潜水及上浮，其中直线前游与后游均能通过BCF及MPF模式实现。样机试验表明机器鱼的直线前向游速随着身体波动频率增大而呈近似线性增大，随着相邻关节相位差的增大而减小。

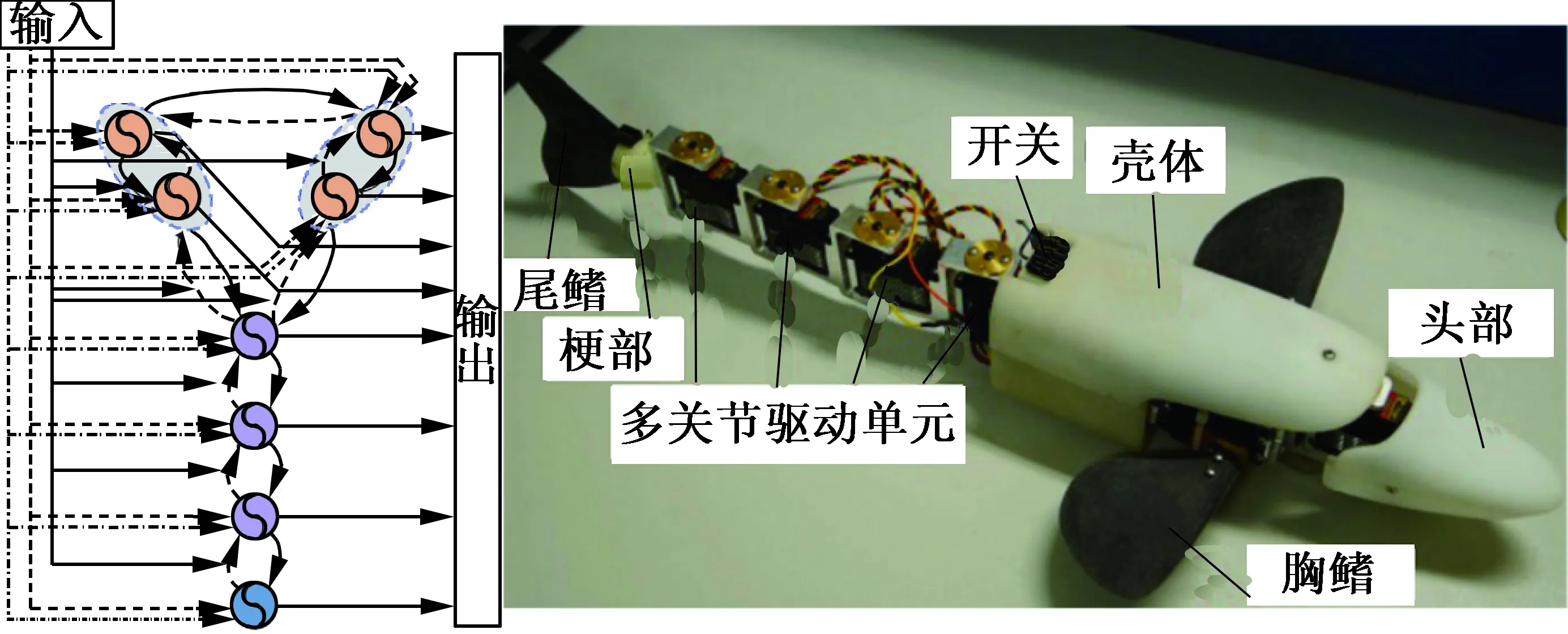
图11 仿白斑狗鱼机器人[24]

Zhou[25]等人设计了含有8个运动鳍条的仿魔鬼刀鱼长鳍波动推进器，并对其进行了CPG控制系统的建模，同传统的正弦发生器控制方法进行了比较。CPG控制方法能较好地克服后者所呈现出来的不足，而且对于波动推进器来说，CPG控制系统产生的波形可以是非谐波波形。后来又通过将遗传算法在线应用于CPG控制模型的9个输入参数的优化选取中，同时引入速度与能量效率反馈，构成了实时闭环控制系统，使得整个控制系统更加智能，成功实现了机器人的高效率鳗状游动，整个控制系统如图12所示。

图12 NKF-III水下机器人[26]

Hu[27]等人设计了一种模仿鲔行式鱼类的高机动性机器鱼，如图13所示。该机器鱼带有胸鳍、背鳍、腹鳍及半月形的尾鳍，并且尾鳍由一个平行四连杆机构进行传动控制，身体为鱼雷形刚性体，而不是柔性体，使得整个鱼体耐水压能力更强。整个控制系统由两个单向耦合的Hopf振荡器构成，实验显示当尾鳍摆动频率达到2.8 Hz时，直线游动速度可达2.0 m/s，而且机动性较好，很容易进行机动转弯控制。

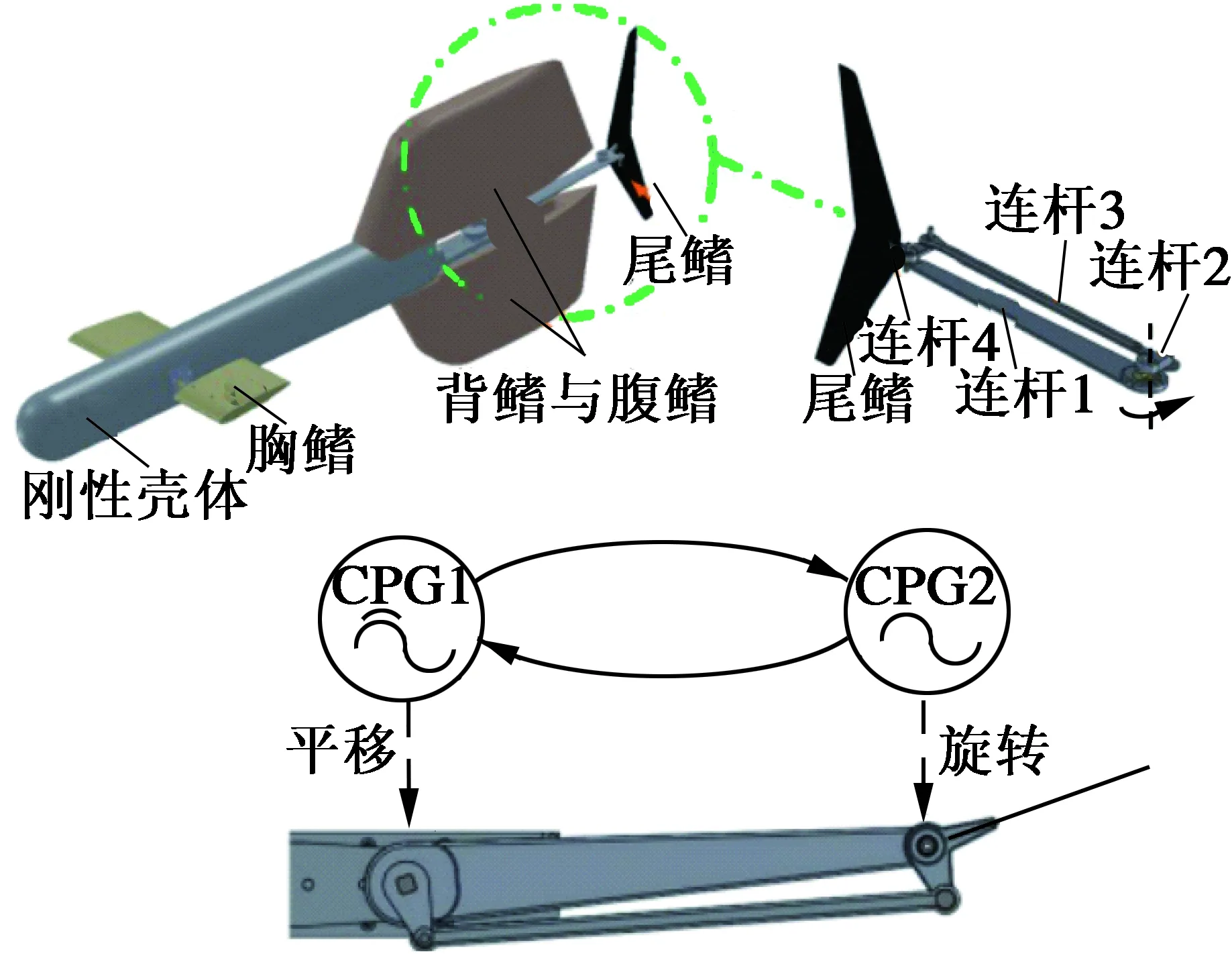
图13 鲔行式仿生机器鱼[27]

3 水下仿生机器人CPG控制关键技术

水下仿生机器人的仿中枢神经元网络控制方法，是为了实际工程上应用而采取的对生物体内动物节律运动控制区——中枢模式发生器(CPG)的工程近似模拟，形成一种控制更加直观、灵活并且易于计算机编程实现的控制方法，实现机器人的节律性运动，提高机器人在各种实际非结构化的工作环境中的工作性能。

总的来说，CPG模型主要有以下优点：

1)CPG模型具有很强的鲁棒性，能够在状态变量短暂的扰动下迅速回到正常节律状态，这对于水下仿生机器人来说具有重要意义。尤其当机器人实现类似于仿生原型的机动性规避动作时，需要快速恢复到定常周期性游动，这一点通过CPG模型很容易实现；

2)CPG模型很容易用来构建分布式网络，因此在模块化机器人和可重构机器人中被大量使用，而且CPG很容易协调机器人的多自由度运动，因此很容易用于多鳍、多关节的机器鱼的运动控制上；

3)CPG模型只需要少量的控制参数就能控制复杂的节律运动，很容易对速度、方向以及运动步态等进行调节，而且当控制参数突变时，CPG生成的过渡轨迹也相当平滑，对于水下机器人而言，可以使机体在不同游动模式切换时实现柔性的过渡；

4)通过振荡子之间的相位差锁定，可以产生多种稳定的相位差关系，实现机器人多样的运动步态，因此很容易用CPG模型构建蛇形机器人的控制系统；

5)CPG模型很容易和感觉反馈信号整合在一起，可以将感觉反馈信息作为CPG模型的微分方程的耦合项；即使在没有感觉反馈信号和中央控制输入的情况下，也能产生不同模式的节律输出，结合水下机器人所能感知的水流流场信息，可使机器人游动更加稳定；

6)CPG模型可以和学习算法及优化算法结合在一起用于机器人中[28]。

但是基于CPG的方法也有两个主要方面的不足：缺少一个成熟的针对指定运动设计CPG模型的理论；描述CPG模型的理论基础仍不完善，现有的CPG模型较不统一，而且一般都包含较为复杂的非线性环节，有时很难证明一个完全基于CPG模型的机器人的稳定性。

当对一个具体应用对象构建一个CPG仿生模型时，主要确定以下5个方面：CPG模型的架构(主要包括CPG模型的类型和神经元的数量)；神经元连接的类型和拓扑结构(这会影响最终生成步态的同步性)；波形(这会影响最终由每个关节角生成的最终轨迹)；输入信号的影响(如输入信号是如何影响输出信号频率、幅值与相位或者波形的)；反馈信号的影响(如环境中的信息反馈是如何影响CPG的节律活动的)。

设计一个CPG模型的主要问题就在于以上5个方面是紧密相互联系的。

目前广泛应用的设计CPG模型的方法主要有以下几种：1)利用动力学系统理论[29]。动力学系统理论能够确定什么时候耦合振子发生共振，以及能够确定什么相位差是稳定的与不稳定的。2)利用学习与优化算法[30]。这类算法主要分为两类，有人监督学习与无人监督学习。在CPG的步态知道的情况下一般采用有人监督学习，而在CPG的产生的步态不明确的情况下一般采用无人监督学习。

以上方法，一般主要用于工程目的，也能用来验证生物CPG模型理论。

4 总结与展望

从数学建模的思想上来看，CPG模型可分为两类，一类为仿生物神经元模型，另一类为非线性振荡子模型。仿神经元模型由生物学上神经冲动传导的过程建模而来，有明确的生物学意义，但在实际的物理系统中使用难度较大，且有太多耦合参数，参数之间的耦合关系较难确定，并且难以整定参数。Kimura递归神经振荡器就属于仿神经元模型。而非线性振荡子模型是在数学上对生物节律性行为的近似，参数较少，易于实际的工程使用。Ijspeert七腮鳗型相位振荡器与Hopf神经振荡器属于此类模型。

随着CPG理论研究的深入，以及计算机仿真技术的发展，CPG控制将具有更好的环境适应性，运动模式更加丰富，并且CPG参数的整定将更加简单与智能化，为水下仿生机器人从形似发展到神似提供控制理论基础。

[1] IJSPEERT A J.Central pattern generators for locomotion control in animals and robots:A review[J].Neural Networks,2008,21(4):642-653.

[2] 童秉纲，庄礼贤.描述鱼类波状游动的流体力学模型及其应用[J].自然杂志,1998,20(1):1-7.

[3] LIGHTHILL M J.Aquatic animal propulsion of high hydromechanical efficiency[J].Journal of Fluid Mechanics,1970,44(11):265-301.

[4] SPINA G L,SFAKIOTAKIS M,TSAKIRIS D P,et al.Polychaete-like undulatory robotic locomotion in unstructured substrates[J].IEEE Transactions on Robotics,2007,23(6):1200-1212.

[5] LOW K H.Mechatronics and buoyancy implementation of robotic fish swimming with modular fin mechanisms[J].Proceedings of the Institution of Mechanical Engineers,2007,221(3):295-309.

[6] BROWN T G.The intrinsic factors in the act of progression in the mammal[J].Proceedings of the Royal Society of London B:Biological Sciences,1911,84(572):308-319.

[7] BROWN T G.On the nature of the fundamental activity of the nervous centres; together with an analysis of the conditioning of rhythmic activity in progression,and a theory of the evolution of function in the nervous system[J].The Journal of Physiology,1914,48(1):18-46.

[8] DELVOLVE I,BRANCHEREAU P,DUBUC R,et al.Fictive rhythmic motor patterns induced by NMDA in an in vitro brain stem-spinal cord preparation from an adult urodele[J].Journal of Neurophysiology,1999,82(2):1074-1077.

[9] WILSON D M.The central nervous control of flight in a locust[J].Journal of Experimental Biology,1961,38(2):471-479.

[10] DELCOMYN F.Neural basis of rhythmic behavior in animals[J].Science,1980,210(4469):492-498.

[11] GRILLNER S.Neural control of vertebrate locomotion-central mechanisms and reflex interaction with special reference to the cat[M].Berlin:Springer Netherlands,1985.

[12] CHENG J,STEIN R B,JOVANOVIC K,et al.Identification,localization,and modulation of neural networks for walking in the mudpuppy (Necturus maculatus) spinal cord[J].Journal of Neuroscience,1998,18(11):4295-4304.

[13] MATSUOKA K.Sustained oscillations generated by mutually inhibiting neurons with adaptation[J].Biological cybernetics,1985,52(6):367-76.

[14] KIMURA H,FUKUOKA Y,NAKA MURAH.Biologically inspired adaptive dynamic walking of the quadruped on irregular terrain[J].Robotics Research,2000:329-336.

[15] 王龙,谭民,曹志强,等.基于CPG模型的仿生机器鱼运动控制[J].控制理论与应用,2007(5):749-755.

[16] TANGORRA J L,MIGNANO A P,CARRYON G N,et al.Biologically derived models of the sunfish for experimental investigations of multi-fin swimming[C]//2011 IEEE/RSJ International Conference on Intelligent Robots and Systems,2011:580-587.

[17] JEONG I-B,PARK C-S,NA K-I,et al.Particle swarm optimization-based central patter generator for robotic fish locomotion[C]//2011 IEEE Congress of Evolutionary Computation,2011:152-157.

[18] IKEDA M,HIKASA S,WATANABE K,et al.A CPG design of considering the attitude for the propulsion control of a Manta robot[C]//39th Annual Conference of the IEEE Industrial Electronics Society,2013:6354-6358.

[19] IJSPEERT A J,CRESPI A,RYZKO D,et al.From swimming to walking with a salamander robot driven by a spinal cord model[J].Science,2007,315(5817):1416-20.

[20] CRESPI A,LACHAT D,PASQUIER A,et al.Controlling swimming and crawling in a fish robot using a central pattern generator[J].Autonomous Robots,2007,25(1-2):3-13.

[21] CAO Y,BI S,CAI Y,et al.Applying central pattern generators to control the robofish with oscillating pectoral fins[J].Industrial Robot,2015,42(5):392-405.

[22] YU J,WANG M,SU Z,et al.Dynamic modeling of a CPG-governed multijoint robotic fish[J].Advanced Robotics,2013,27(4):275-285.

[23] 汪明,喻俊志,谭民.胸鳍推进型机器鱼的CPG控制及实现[J].机器人,2010,32(2):248-255.

[24] WU Z,YU J,SU Z,et al.An improved multimodal robotic fish modelled after Esox lucius[C]//2013 IEEE International Conference on Robotics and Biomimetics,2013:516-521.

[25] ZHOU C,LOW K H.Kinematic modeling framework for biomimetic undulatory fin motion based on coupled nonlinear oscillators[C]//23rd IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems,2010:934-939.

[26] ZHOU C,LOW K H.Optimization of swimming locomotion for fish robots with multi-actuation[C]//2011 IEEE International Conference on Robotics and Biomimetics,2011:2120-2125.

[27] HU Y,ZHANG S,LIANG J,et al.Development and CPG-based control of a biomimetic robotic fish with advanced underwater mobility[C]//2014 IEEE International Conference on Robotics and Automation,2014:813-818.

[28] CRESPI A,IJSPEERT A J.Online optimization of swimming and crawling in an amphibious snake robot[J].IEEE Transactions on Robotics,2008,24(1):75-87.

[29] COHEN A H,HOLMES P J,RAND R H.The nature of the coupling between segmental oscillators of the lamprey spinal generator for locomotion:A mathematical model[J].Journal of Mathematical Biology,1982,13(3):345-369.

[30] PEARLMUTTER B A.Gradient calculations for dynamic recurrent neural networks:A survey[J].IEEE Transactions on Neural Networks,1995,6(5):1212-1228.