如何教才能做到“不重不漏”
2017-05-02周怀君
文︳周怀君
如何教才能做到“不重不漏”
文︳周怀君
小学数学教材里有搭配、数线段、数角的个数之类的问题,学生常出现的问题是重复或遗漏。教学时,如何教才能使学生不出现重复或遗漏的错误呢?
学生为什么在计数时会出现重复或遗漏?首先要找的原因是老师的教。教“2件上衣,3条裤子,一件上衣与一条裤子搭配成一套,有几种搭配方法?”时,在学生完成了解答后,老师们常是这样总结的:我们做这种搭配题时,要做到有序思考,不重复、不遗漏。至于如何有序思考,如何才能不重复、不遗漏却没有了下文。事实上,老师如果教给学生思考问题的方法,这些问题就可得到解决。
首先是分类。上衣与裤子分为两类,上衣标上数字序号1、2,裤子标上字母序号A、B、C。标上序号,便于表达。
其次是连线。连线时,先从上衣1号开始,分别与裤子A、B、C连线,然后是上衣2号分别与裤子A、B、C连线(见图1)。这就是有序。有了这个序,才能保证不重复、不遗漏。
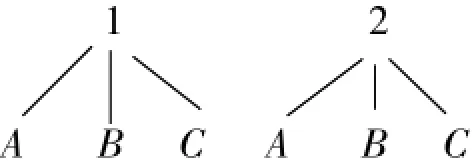
图1
最后是计数。最好采用分类计数的办法,即从上衣1号出发有3条线,从2号出发也有3条线,故共有3+3=6(条)线,也就是有6种搭配方式。当然,也可以一一数出线的条数是6,但这种方法不那么好,因为没有体现出前面分类的思路。
又如,甲、乙、丙3人从排成一排的8个位置中选择3个,甲不能站在最左端的3个位置,乙不能站在最右端的3个位置,丙不能站在两端。甲、乙、丙有几种站法?
做这个题时很容易出现重复或遗漏,因为甲、乙、丙站的位置受限制的条件多。怎么办呢?回忆波利亚写的《怎样解题》中的话:画个图,如何?将8个位置用数字1~8表示(如图2所示)。有了图,且标上了数字,就便于表达了。甲只能站4、5、6、7、8号位,乙只能站1、2、3、4、5号位,丙只能站2、3、4、5、6、7号位。

图2
若甲站4号位,则乙只能站1、2、3、5号位。这时,若乙站1号位,则丙只能站2、3、5、6、7号位。其他情况依次类推。将上述过程用图3表示就一目了然。

图3
这样,甲站4号位一共有17种站法。而甲站5号位与站4号位的站法是一样多,也是17种站法。
甲站6号位与7号位的站法也是一样多,都是21种,站8号位有26种,具体站法见图4。因此,一共有17+17+21+21+26=102(种)站法。

图4
从上述两个例子可以看出,要做到不重复、不遗漏,老师要指点防止重复或遗漏的方法。方法的获得,必须要有学生的独立思考与独立解答的环节作保证。因此,在教解这些题时,老师不能过多地讲解,而要让学生独立思索一阵子,再根据情况确定讲解的内容。
如上面选位置,学生先做几分钟,答案肯定五花八门,没关系,典型的错误有下面几种。
甲有5种站法,乙有5种站法,丙有6种站法,那么一共有5×5×6=150(种)站法。这里就包括了许多重复的站法。甲有5种站法,每种站法对应的乙就不是5种。从图3可以知道,甲站4号位时,乙就只有4种站法,不是5种。同样地,丙对应的每种站法就不是6种,从图3可以明显地看出。因此,出现了许多重复的站法。一旦做出结果后,要想找出重复的站法相当困难。所以,在解决计数问题时,选择思考的方法很重要,会影响到后面的思考。在小学阶段,建议老师们采用分类、逐步推进的办法,可以有效地解决计数难的问题。
(作者单位:汉寿县岩汪湖中学)
人教版小学数学教材五年级下册观察物体(三)的单元小结(如图1所示)中讲道:“根据三个方向观察到的形状摆小正方体,结果只有一种哦!”根据三视图摆小正方体,结果只有一种吗?笔者通过对几个例题的研究,发现这一结果不全面。

图1
例1一个由相同的小正方体木块组成的立体图形,从正面、左面、上面看到的平面图形如图2所示,你能摆出这个立体图形吗?
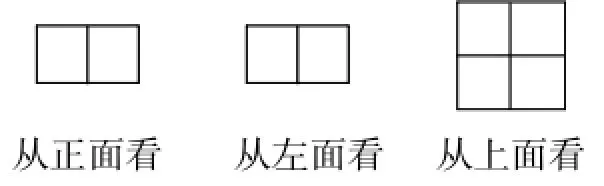
图2
