改进自适应卡尔曼滤波的拖拉机驱动轮滑转率估计
2017-05-02周志立徐立友
周志立,刘 尧,徐立友
(河南科技大学 车辆与交通工程学院,河南 洛阳 471003)
改进自适应卡尔曼滤波的拖拉机驱动轮滑转率估计
周志立,刘 尧,徐立友
(河南科技大学 车辆与交通工程学院,河南 洛阳 471003)
针对拖拉机驱动轮滑转率估计中存在的精度低和实时性差等问题,建立了拖拉机滑转率测量系统的模型。对传统Sage-Husa自适应卡尔曼滤波算法,从计算步骤简化和噪声估计简化两方面进行了改进,编写了MATLAB程序并与多种算法进行了对比分析。仿真结果表明:改进的变结构Sage-Husa自适应数据融合算法能估计噪声的统计特性,在不进行误差统计试验的前提下,实现了对拖拉机驱动轮滑转率的实时准确估计。驱动轮滑转率在白噪声的干扰下鲁棒性较好,平均误差为中值滤波算法的16%左右。
农业机械;拖拉机;卡尔曼滤波;滑转率;信息融合;驱动轮
0 引言
随着农业的发展,耕地越来越集中化,大中型拖拉机更多地应用在田间作业中,如何提高拖拉机的作业效率变得尤为重要。拖拉机在农田作业时,土壤松软和地面不平会使驱动轮出现滑转情况,影响拖拉机各项性能的发挥。文献[1]研究了驱动轮滑转对驱动性能的影响。文献[2]计算了履带车辆在松软土壤上行驶时,滑转率与地面牵引力的关系。文献[3]提出了根据滑转率对拖拉机的耕作深度进行精确控制的方法,驱动轮的滑转率是其控制系统的重要参考依据。以上研究说明滑转率是一项重要的拖拉机性能参考指标。
计算滑转率精确值的关键在于实际速度和驱动轮理论速度的实时准确测量,由于干扰噪声的存在,仅使用轮速传感器和全球定位系统(global positioning system,GPS)信号的简单测量方法达不到测量精度的要求。为了实时精确测量拖拉机驱动轮的滑转率,很多学者使用多普勒雷达和光电传感器等高精度检测设备[4-5]。由于受拖拉机制造和使用成本的制约,这些设备目前并未在量产拖拉机上广泛使用。文献[6]设计了拖拉机滑转率测试系统,并建立了虚拟样机进行测试。测量驱动轮的滑转率需要驱动轮的理论速度与实际车速两个参数,但测量信号容易受到噪声的干扰,而且滑转率的计算过程对噪声的输入有放大作用,如果不采取合适的滤波算法对测量信号进行处理,噪声遍布整个测量信号范围,会导致滑转率测量精度较差。
卡尔曼滤波信息融合算法已经广泛应用于汽车状态估计中,防抱死制动系统(anti-lock braking system,ABS)、电子稳定程序(electronic stability program,ESP)等系统能否有效地工作,很大程度上依赖于是否有准确、实时的横摆角速度、质心侧偏角和车速等车辆状态作为其信号输入[7-9]。拖拉机在田间作业时车速并不高,对测量与控制系统的响应速度要求低,同时对滤波算法的计算速度要求也相应降低。目前,应用于农用车辆和机具的农林车辆串行数据通信与控制网络标准(ISO 11783),为多传感器的信息融合提供了良好的平台,多个传感器可以通过控制器局域网络(controller area network,CAN)连接,并可以互相交换信息。针对在拖拉机滑转率精确估计中存在的精度低与实时性差等问题,本文设计了自适应卡尔曼滤波算法,在线估计传感器信号的测量噪声方差,并使用卡尔曼滤波信息融合算法将多个低成本传感器的信号用于精确计算拖拉机滑转率。
1 驱动轮滑转率测量系统及建模
首先,建立系统状态方程,将拖拉机在作业时的实际车速和理论车速进行3阶泰勒级数展开;然后,进行离散化处理,应用轮速传感器、车身加速度传感器和角加速度传感器对系统进行观测,构成系统观测器Z。状态空间模型[10]表达式为:

(1)
其中:x(k)为k时刻的系统状态向量;z(k)为k时刻的系统测量值;φ(k)为系统状态矩阵;H(k)为观测矩阵;W(k)和V(k)是相互独立的带时变均值和协方差的高斯白噪声,方差分别为Q(k)和R(k)。
x(k)=[v(k)a(k)a(k)′vq(k)aq(k)aq(k)′]T,
其中:v(k)为实际车速,m/s;a(k)为车身加速度,m/s2;a(k)′为车身加速度变化率,m/s3;vq(k)为驱动轮理论速度,m/s;aq(k)为驱动轮理论加速度,m/s2;aq(k)′为驱动轮理论加速度变化率,m/s3。
以计算k+1时的车速为例,v(k+1)=v(k)+a(k)·△t+0.5a(k)′△t2,化为矩阵形式得到φ:
实际可测量值为v(k)、a(k)、vq(k)和aq(k),根据式(1)得到H(k)=diag(1,1,0,1,1,0)。
z(k)=[ωwh(k)·rd av(k) 0 ωqwh(k)·rq ε(k)·rq 0]T,
其中:rd为从动轮滚动半径,m;rq为驱动轮滚动半径,m;ε(k)为驱动轮角加速度传感器信号,rad/s2;av(k)为车身加速度传感器信号,m/s2;ωwh(k)为从动轮转速传感器信号,rad/s;ωqwh(k)为驱动轮轮速传感器信号,rad/s。
由卡尔曼滤波后的系统状态向量可以求出驱动轮滑转率:
(2)
其中:δ(k)为驱动轮滑转率,是一个绝对值小于1的比值。
测量驱动轮轮速时,不经过滤波直接计算滑转率的公式为:
(3)
2 改进的Sage-Husa变结构自适应卡尔曼滤波信息融合算法
Sage-Husa自适应滤波算法虽然能实时动态地调整过程噪声和测量噪声的统计特性,但存在运算量大、状态估计容易发散等问题[11]。考虑到拖拉机滑转率计算的实时性要求比较高,同时受拖拉机嵌入式测控系统计算速度的影响,适当地简化Sage-Husa自适应滤波算法可以提高计算速度,使滑转率估计的实时性得到保障。本文在以下3个方面对Sage-Husa自适应卡尔曼滤波算法进行改进:
(4)
改为:
(5)
原因主要有两点:①Sage-Husa变结构自适应卡尔曼滤波只能在Q、R两者之中有一个已知的情况下估计出另外一个。本文假设系统噪声具有稳定性,仅对观测噪声进行估计。②经过补偿之后的系统噪声具有一定的鲁棒性,而测量噪声主要来源于外界环境因素,具有较大的不确定性[12]。所以对测量噪声进行自适应调整更符合实际情况。
(Ⅱ)酌情减小测量噪声协方差矩阵估计的无偏性。将观测噪声方差公式
H(k+1)P(k+1,k)HT(k+1)]
(6)
改为:
(7)
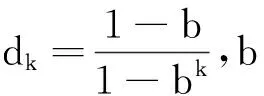
如果滤波过程中出现收敛的趋势,误差协方差矩阵会逐渐减小,直至趋于0,并且观测矩阵H是定值,那么H(k+1)P(k+1,k)HT(k+1)的值会变小直至趋于0,因此其对测量噪声协方差的影响可以忽略。
(Ⅲ)每次滤波过程都要重复计算观测噪声的统计特性,较高阶的计算会使计算量增加,拖拉机测控系统采样周期较短,计算速度无法满足测量系统对实时性的要求。针对算法实时性不佳的问题,本文提出基于协方差匹配的滤波发散条件来判断滤波是否发生异常。
协方差匹配技术的基本思想是:实际的余项应与它的理论特性“相匹配”,也就是在滤波的同时计算检验实际的余项,判断它是否是相容的,即是否出现滤波异常。当实际的余项与原假设Q(k)、R(k)不相容时,则对Q(k+1)、R(k+1)进行估计来取代原来假设的Q(k)、R(k)[13]。
文献[14]提出的一种判断滤波异常的判据为:
(8)
其中:γ为储备系数,且γ>1;tr为矩阵的迹;ε(k+1)为新息序列。
若式(8)成立,则实际误差将超过理论预计值的γ倍,滤波发散。
假设R(k+1)=R(k),理论上,
(9)
因此,由式(8)和式(9)可以得到滤波异常时的判据为:
(10)
在进行第k次滤波过程中,使用式(10)计算滤波状态,若式(10)成立,则认为实际的余项与原假设R(k+1)=R(k)是不相容的,此时使用式(7)计算R(k+1)并代替R(k);反过来,如果式(10)不成立,则不用计算式(7)。那么有R(k+1)=R(k),从而实现对R(k)的自适应估计。
3 仿真分析
3.1 仿真信号与参数设定
在已建立的数学模型基础上,用MATLAB软件编写程序进行仿真。因为正弦波信号源模块产生的正弦信号非常“纯净”,所以在输入端加入噪声信号源,与正弦波信号源信号合成后,模拟轮速传感器信号、车身加速度计信号、角加速度传感器信号,可以较好地仿真测试出自适应滤波算法的效果。在所有信号上加入均值为信号幅值范围5%的高斯白噪声,噪声方差R=diag(0.112,0.052,0,0.202,0.052,0)。假设在11s时从动轮速度信号受到干扰A,在21s时驱动轮速度信号受到干扰B,连续10个采样点发生畸变,仿真工况选择拖拉机在犁耕工作挡。驱动轮与从动轮速度测量信号分别如图1和图2所示。

图1 驱动轮速度测量信号 图2 从动轮速度测量信号
为了验证改进的Sage-Husa自适应卡尔曼滤波算法对驱动轮滑转率计算的准确性和可靠性,使用MATLAB软件对算法进行了仿真,同时与其他算法下驱动轮滑转率的计算值相比较。算法1:使用滤波窗口宽度为5的一维中值滤波对驱动轮和从动轮转速信号进行处理,并用式(3)计算驱动轮滑转率。算法2:使用改进的Sage-Husa自适应卡尔曼滤波算法对多传感器信号进行信息融合,由式(2)计算驱动轮滑转率。
仿真参数设置:状态向量初始值都为0,协方差初始值都为0.1;采样频率为50Hz;仿真时间为30s;系统误差设为已知Q=diag(0,0.01,0.01,0,0,0.01,0.01);东方红SG350-1型拖拉机的从动轮滚动半径rd为0.26m,驱动轮滚动半径rq为0.35m。
3.2 不同算法下驱动轮滑转率仿真
直接使用驱动轮轮速与从动轮轮速测量原始信号计算得到的驱动轮滑转率如图3所示。
从图3中无法看出驱动轮滑转率的正弦波动特性。在正弦信号中加入了均值为信号幅值范围5%,方差R=diag(0.112,0.052,0,0.202,0.052,0)的高斯白噪声,并且在11s和21s(分别为干扰A和干扰B)加入了畸变。式(3)对噪声信号具有放大作用,如果噪声信号不经任何处理直接用式(3)计算驱动轮滑转率,会导致求出的滑转率值布满噪声干扰,拖拉机控制系统无法使用该滑转率信号。
使用中值滤波算法计算得到的驱动轮滑转率如图4所示。从图4中可以看出:算法1的效果虽然优于原始信号计算得到的驱动轮滑转率,驱动轮滑转率的正弦变化特性明显,但是A点和B点的连续信号畸变对算法1的影响很明显,并且在20s以后由于B点畸变的影响,滤波误差有增大的趋势。

图3 原始信号计算得到的驱动轮滑转率图4 中值滤波算法计算得到的驱动轮滑转率
使用改进的Sage-Husa自适应卡尔曼滤波算法计算得到的驱动轮滑转率如图5所示。由图5可以看出:算法2对加入的畸变信号不敏感,且滤波后的信号曲线较光滑,滤波效果明显优于图3和图4。因为畸变信号在数据融合过程中权值较低而被其他信号修正,驱动轮轮速信号发生畸变时被角加速度信号修正,从动轮轮速信号发生畸变时被车身加速度信号修正,所以多传感器融合系统滤波效果受单个传感器扰动的影响较小。
3.3 误差分析
图6为算法1与算法2的驱动轮滑转率误差比较图。从图6可看出:算法1的误差值在整个计算过程中都比较大且不稳定,在11s与20s畸变处误差值显著增大,可见算法1对突变信号的平滑作用较差。算法2的误差值在整个计算过程中都较小,且误差受突变信号的影响较小,明显优于算法1。
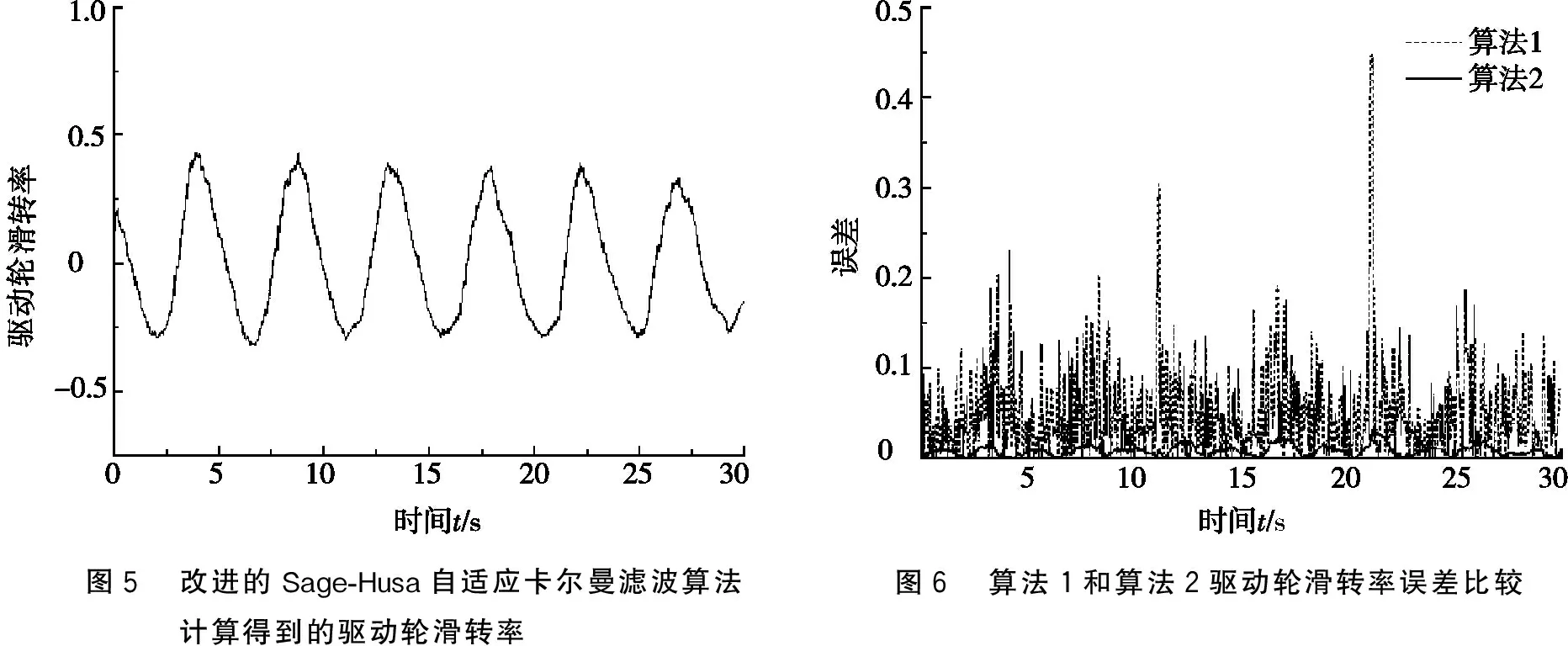
图5 改进的Sage-Husa自适应卡尔曼滤波算法计算得到的驱动轮滑转率 图6 算法1和算法2驱动轮滑转率误差比较
求得算法1的驱动轮滑转率误差平均值为0.052 4,算法2的误差平均值为0.008 8,算法2误差平均值为算法1的16%左右;算法1和算法2误差绝对值的最大值分别为0.466 6和0.030 5。
4 结论
(1)对Sage-Husa自适应卡尔曼滤波算法进行了改进,并且加入变结构算法,简化其运算步骤,使其能应用于拖拉机滑转率实时计算。
(2)编写MATLAB程序,测试提出改进的Sage-Husa自适应卡尔曼滤波算法,得到的驱动轮滑转率误差均值为0.008 8,误差绝对值最大值为0.030 5,平均误差为中值滤波算法的16%左右。
[1] 谷侃锋,王洪光,赵明扬.滑转率对月球车车轮驱动力学特性的影响分析[J].计算机仿真,2008,25(6):25-29.
[2] 韩立军.履带车辆牵引特性的仿真与验证[J].农业装备与车辆工程,2013,51(2):6-8.
[3] 白学峰,鲁植雄,常江雪,等.基于滑转率的拖拉机自动耕深模糊控制仿真[J].农业机械学报,2012,43(2):6-10.
[4]STUCHLYSS,THANSANDOTEA,MLADEKJ,etal.ADopplerradarvelocitymeterforagriculturaltractors[J].IEEEtransactionsonvehiculartechnology,1978,27(1):24-30.
[5]THANSANDOTEA,STUCHLYSS,MLADEKJ,etal.Anewslipmonitorfortractionequipment[J].TransactionsofASAE,1977,10(5):851-856.
[6] 印祥.拖拉机打滑率测试系统及其虚拟测试的研究开发[D].杨凌:西北农林科技大学,2011.
[7] 丁红,赵林峰,周延明,等.基于UKF算法的车辆质心侧偏角估计[J].湖北汽车工业学院学报,2012,26(4):5-9.
[8] 李以农,郝奕,郑玲,等.基于多传感器信息融合的车速估计方法[J].江苏大学学报(自然科学版),2007,28(4):301-304.
[9] 丁红.ESP系统中关键状态参数估计算法研究[D].合肥:合肥工业大学,2013.
[10] 黄小平,王岩.卡尔曼滤波原理及应用[M].北京:电子工业出版社,2015.
[11]RAHEMANH,JHASK.Wheelslipmeasurementin2WDtractor[J].Journalofterramechanics,2007,44:89-94.
[12] 徐林,李世玲,屈新芬.一种稳健的自适应传递对准算法[J].系统仿真学报,2012,24(11):2324-2328.
[13] 张常云.自适应滤波方法研究[J].航空学报,1998,19(7):96-99.
[14] 宋迎春.GPS动态导航定位的当前统计模型与自适应滤波[J].湖南人文科技学院学报,2005,10(5):7-9.
国家自然科学基金项目(51375145);河南省重点科技攻关计划基金项目(102102210165)
周志立(1957-),男,河南偃师人,教授,博士,博士生导师,主要从事车辆新型传动理论与控制技术等方面的研究.
2016-09-13
1672-6871(2017)04-0072-05
10.15926/j.cnki.issn1672-6871.2017.04.015
U463.3
A
