改进的灰色关联分析法在渔业水质评价中的应用

赵龙明，卢琪，王娜，2，阎少宏，2

(1.华北理工大学 数学建模创新实验室，河北 唐山 063210；2.华北理工大学 理学院，河北 唐山 063210)

改进的灰色关联分析法在渔业水质评价中的应用

赵龙明1，卢琪1，王娜1，2，阎少宏1，2

(1.华北理工大学 数学建模创新实验室，河北 唐山 063210；2.华北理工大学 理学院，河北 唐山 063210)

序关系分析；灰色关联；水质评价；综合关联矩阵

水体质量对渔业的产量和质量有着显著影响。为使水质评价结果更加准确，采用改进的灰色关联分析法对池塘的水质进行评价。在确定指标权重时，采用序关系分析法，避免了采用超标倍数法在计算权重时因某项参数超标而使各综合指标评价偏高的缺点，充分考虑到养殖专家的实际养殖经验，使各指标权重更科学合理，水质关联值更为精准，从而使水质等级更符合事实。以某渔业养殖场4个池塘的水质监测数据为计算实例，选取pH、透明度、总氮、溶氧、COD 5个指标，运用该模型计算的结果与实际情况更吻合。

水质评价是一个涉及多因素、多层次结构的非线性系统[1]。目前水质评价的主要方法有物元分析法、综合污染指数法、神经网络法、灰色关联分析法等[6]。灰色系统理论是水质评价方法研究上一个较成熟的理论[2]。在灰色关联分析法中，权重的计算对评价结果有很重要的影响。以往文献中较常采用超标倍数赋权法[2]，但其面对多个评价对象时，需要分别计算每个对象的各评价指标的权重值，运算量过大，且不能考虑到不同监测点位间的相互关系，导致评价结果不够准确[4]。该项研究将序关系分析引入渔业水质评价指标的权重的计算中，能够充分考虑到渔业养殖专家在养殖水质上积累的实际经验，从而给予指标更科学合理且符合养殖需求的权重，使最终结果更具渔业养殖的实际参考价值，此外，该方法计算更加简便。

该项研究将基于序关系分析的灰色关联分析法应用到某地4个池塘的水质评价中，以期得到更为准确的评价结果，为渔业水质的管理决策提供更具渔业养殖意义的判断依据。

1 序关系分析法确定权重

1.1 确定指标的序关系

1.2 相邻指标重要程度赋值

rk=ωi-1/ωi

(1)

式中，ωi、ωi-1分别为第i、i-1项指标权重。

权重在计算前是未知的，而rk可以通过专家对两两指标间的重要程度评价打分获得。指标的相对重要程度rk赋值见表1。

表1 相邻指标相对重要程度

1.3 计算各指标权重

根据式(1)可知:

(2)

(3)

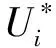
2 建立灰色关联分析评价模型

2.1 建立池塘水评价指标体系矩阵

定义X(T)为评价水体对应于m个指标与一个池塘的n个断面的多指标样本矩阵，则

(4)

时间T是评价样本的不同时间序列。

2.2 水体评价标准矩的建立

结合《渔业用水水质标准》[9](GB11607-1987)的要求，采用《地表水环境质量标准》[8](GB3838-2002)建立水质评价标准分类矩阵。

(5)

2.3 矩阵归一化

因各评价指标的单位不完全相同需将矩阵进行归一化即无量纲化处理，并定义最优级水质为I类，最差级水质为V类(I与V类之间的转换按下列公式进行)

(1)对于数值越大代表越超标的指标项(如TN、CODMn)按下列公式分别变换为X、S矩阵

(6)

bti=(sci-sti)/(sci-sli)

(7)

(2)对于数值越大代表越好的指标项(例如OD)按下列公式分别变换为X、S矩阵

(8)

bti=(sti-sci)/(sli-sci)

(9)

(3)关联离散函数ξi(aj,bt)的确定

(10)

2.4 计算关联度建立综合关联评价分析矩阵

待评价水体样本aj与第bt等级水质标准间的关联度表示，即

(11)

其中Wji为第j个样本第i个指标的权重。

2.5 确定权重系数

在实际问题中指标与指标之间的重要程度是不同的。在研究采样点水质时充分考虑到养殖专家的实际养殖经验对水体质量的要求，在确定各指标权重时采用序关系分析法确定权重。

3 实例应用

提取某地4个池塘的水质监测资料(如表2所示)，对监测点的5个常规监测项目(pH、透明度、总氮、溶氧、COD)进行分析，其中1#、2#池塘主要放养虾类，3#、4#池塘主要放养鱼类。

表2 各池塘监测项目数据

3.1 应用序关系法确定各采样点指标权重

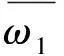
表3 专家对重要指标序关系排列及rk赋值

3.2 用灰色关联对样本采样点进行数据处理

再按照公式(8)得出采样点水评价标准矩阵:

将X14@5、S5@5矩阵带入灰色关联度程序用MATLAB软件解得第1周1～4号池塘综合关联矩阵：

3.3 结果分析

根据综合关联矩阵分析，由隶属最大原则得第1周1#池塘属于3级水质，2#池塘属于4级水质，3#池塘属于3级水质，4#池塘属于4级水质。同理，解得其余周数的综合关联矩并评价其水质等级。根据解得的结果绘制成水质等级随周数的折线变化如图1所示 。

图1 池塘水质等级折线图

由以上结果得出：1#池塘水体总体属于2级、3级之间，2#池塘水体总体也属于2级、3级之间，但更偏向于2级，3#、4#池塘水质均在3级左右较规律的波动，总体属于3级。由以上分析结果可以看出，池塘水质总体属于中度污染状态。

由折线图可知，池塘水质还与养殖的动物类型有关。鱼池水体质量明显波动较大，而虾池水体质量波动较小，且虾池总体水质优于鱼池水体，该种情况可能与鱼和虾的活跃性及各自对食物摄取种类有关。

4 结论

(1)为避免超标倍数法计算权重时因某项参数超标而使各项综合指标评价偏高的缺点，考虑养殖专家的实际养殖经验，采用序关系分析法确定权重，使各指标权重更科学合理，进而使水质评价结果更具实际参考价值。

(2)通过结合序关系分析和灰色理论，建立了改进的灰色关联分析法，将其应用于渔业水质评价，并以某地的4个池塘为例，进行实际运用。结果表明，采用改进后的灰色关联分析法评价渔业水质所得的结果，更符合当地的实际淡水池塘水质。运用序关系分析法对灰色理论进行补充改进，对灰色理论的发展和推广具有重要意义。

[1] 刘博,肖长来,田浩然,等. 灰色关联和层次分析法在地下水质评价中的应用——以吉林市为例[J]. 节水灌溉,2013,38(01 ):26-29.

[2] 赵天龙. 灰色关联分析法在淡水鱼类养殖池塘水质评价中的应用[D].南宁：广西大学,2012.

[3] 翟国静. 灰色关联分析在水质评价中的应用[J].水电能源科学,1996,1403 :183-187.

[4] 彭文启,张祥伟.现代水环境质量评价理论与方法[M].北京:化学工业出版社,2005:32-35.

[5] 李晓雪,卢新卫. 基于熵权的西安市大气环境质量模糊综合评价[J]. 环境科学与技术,2012,35(04):195-199.

[6] 卢文喜,李迪,张蕾,等. 基于层次分析法的模糊综合评价在水质评价中的应用[J]. 节水灌溉2011,36(03 ):43-46.

[7] 陈陌,郭亚军,于振明. 改进型序关系分析法及其应用[J].系统管理学报,2011,20(03):352-355.

[8] GB/T14848-93，地下水环境质量标准[S].

[9] GB11607-1987，渔业用水水质标准[S].

Application of Improved Grey Correlation Analysis Method in Fishery Water Quality Assessment

ZHAO Long-ming1, LU Qi1, WANG Na1,2,YAN Shao-hong1,2

(1.Innovation Laboratory of Mathematical Modeling,North China University

ofScienceandTechnology,TangshanHebei063210,China;2.CollegeofScience,NorthChinaUniversityofScienceandTechnology,TangshanHebei063210,China)

order relation analysis; grey correlation; water quality evaluation; comprehensive incidence matrix

water quality has a significant impact on the yield and quality of fishery. In order to make the water quality assessment results more accurate, the improved grey correlation analysis method was used to evaluate the water quality of the pond. When determining the index weight, the order relation analysis method avoid the shortcomings of the excessive multiples method in the calculation, which make the evaluation of comprehensive index too high because a certain parameter exceeds the standard of evaluation, and this method fully consider the actual experience of aquaculture aquaculture experts, the weight of each index is more scientific and reasonable, the water quality association is more accurate, thereby making the water level more in line with the facts. Taking the water quality monitoring data of four ponds of a fishery farms for example, Five indicators such as pH, transparency, total nitrogen, dissolved oxygen, COD were selected , The result calculated by the model is more consistent with the actual situation.

2095-2716(2017)02-0110-06

2016-11-07

2017-03-26

国家青年基金资助项目(No.11301120)。

S932

A