基于马尔科夫过程的频谱接入建模与分析
2017-05-02苗成林
苗成林, 吕 军, 李 彤, 常 成
(陆军装甲兵学院信息通信系, 北京 100072)
随着现代战争中电子对抗的日益激烈,军事通信对可靠性和抗毁性的要求也愈加强烈。认知无线电技术能够在通信条件恶劣的战场环境建立可靠、抗毁伤的通信链路,适用于各种作战通信任务。认知无线电是指认知用户(Secondary User,SU)利用授权用户(Primary User,PU)的空闲频段传输数据,一旦检测到PU重新使用时,马上撤离该授权频段,避免频谱冲突[1]。频谱接入是认知无线电中共享频谱、提高频谱利用率的关键技术,也是认知过程的重要环节。目前,对频谱接入的研究是为了解决感知到可用频谱后如何接入信道的问题,多采用智能算法以增加信道吞吐量和提高接入效率来优化频谱接入性能,智能算法包括神经网络[2]、遗传算法[3]、博弈论[4]和马尔科夫模型[5-9]等。利用神经网络分析频谱接入时,主要基于频谱预测来提高频谱接入性能,但神经网络的许多内部参数主要靠经验配置,运算的可解释性较差;遗传算法受限于复杂的遗传模型,计算复杂度高;博弈论多从频谱分配的角度分析频谱接入性能,无法分析频谱接入行为;而马尔科夫模型能够用完备的数学表达式描述频谱接入过程,其可分为连续马尔科夫链模型、部分观测马尔科夫模型(Partially Observable Markov Decision Processes,POMDP)[5]、隐马尔科夫模型(Hidden Markov Model,HMM)[6]3类。POMDP多用于认知无线电的感知-接入联合策略,可求得最佳接入策略,但无法具体描述接入过程[5]。HMM能够根据历史感知数据优化接入性能,灵活性强,但该方法需要先验训练模型,具有一定的局限性[6]。基于连续马尔科夫链的信道接入模型能够对信道状态进行预测,建立具体的频谱接入过程模型[7],因此笔者采用连续马尔科夫链模型来优化频谱接入性能。
在多SU频谱接入性能研究方面,FAN等[8]从信道感知的角度,研究了实现最大频谱效率的接入机制;SHOKRI等[9]从多用户竞争信道的角度,研究了减小冲突、提高信道吞吐量的频谱接入机制。然而以上研究侧重于频谱接入的性能优化机制,忽略了具体的频谱接入过程。基于此,笔者针对军事应急网络接入现有通信网络的战术场景,重点研究2个不同优先级SU的具体频谱接入过程,计算连续马尔科夫链模型中各用户到达、退出行为对其他用户的影响,采用阻塞概率、切换概率和中断概率对接入性能进行评估,分析不同用户的通信行为对频谱接入性能的影响。
1 系统模型
军事应急网络接入到通信网络,构成的通信环境如图1所示,包括授权信号、背景噪声、跳频信号和网间干扰。其中应急网络和邻近网络是SU网络,以网间干扰最小为目标设置各自的跳频通信制式。邻近网络用户是高优先级SU,称为SUH,应急网络用户是低优先级SU,称为SUL,基站是PU,
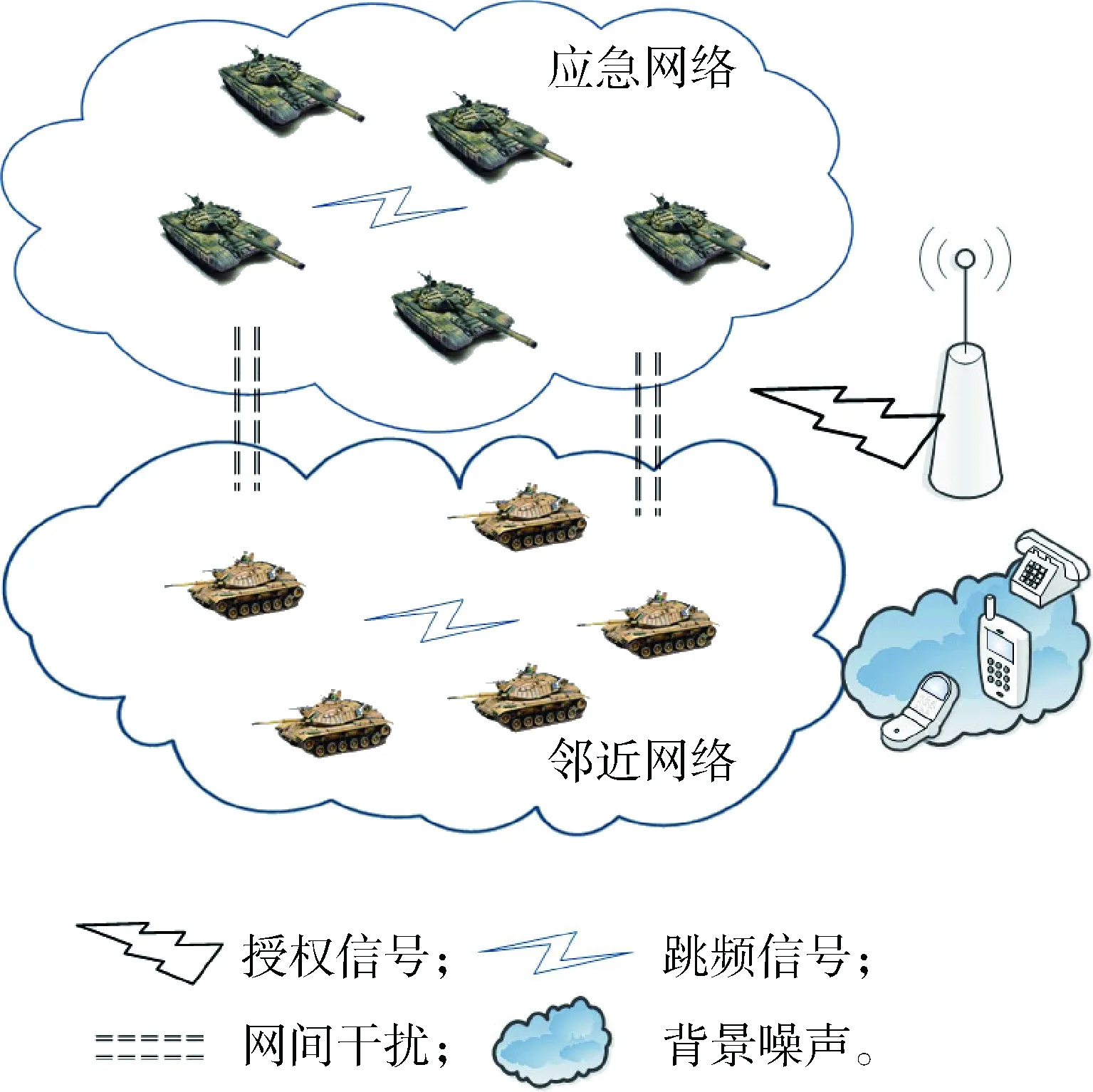
图1 通信环境
对频谱的使用优先级顺序为PU>SUH>SUL。
PU网络是宽带通信系统,每个PU的授权信道带宽为BPU,共有M个PU,记为PUi(i=1,2,…,M)。SU网络是窄带通信系统,将每个BPU分成N个子信道,每个SUH和SUL分别需要N1和N2个子信道(N1>N2)。当其中一个PU返回授权信道时,正在使用该信道下子信道的SUH和SUL都需要切换到其他子信道下。PU、SUH和SUL在系统中的数量分别为i、j、k。
PU与SU的出现服从“类随机分布”,属于一种以有限用户数为基础的模型,统计为截断的泊松分布,业务达到率与用户数量有关。大多数通信系统用户的到达情况可用泊松分布进行描述[10],令用户到达时间服从参数为λ的泊松分布。
2 频谱接入过程
2.1 授权用户到达、退出信道
PU到达信道时,其到达速率为λP,根据空闲子信道数可分为以下3种情况:
1) 空闲子信道数≥N,即(i+1)N+jN1+kN2≤MN,PU到达后占据了N条空闲子信道,状态转移为(i,j,k)→(i+1,j,k)。
2) 空闲子信道数
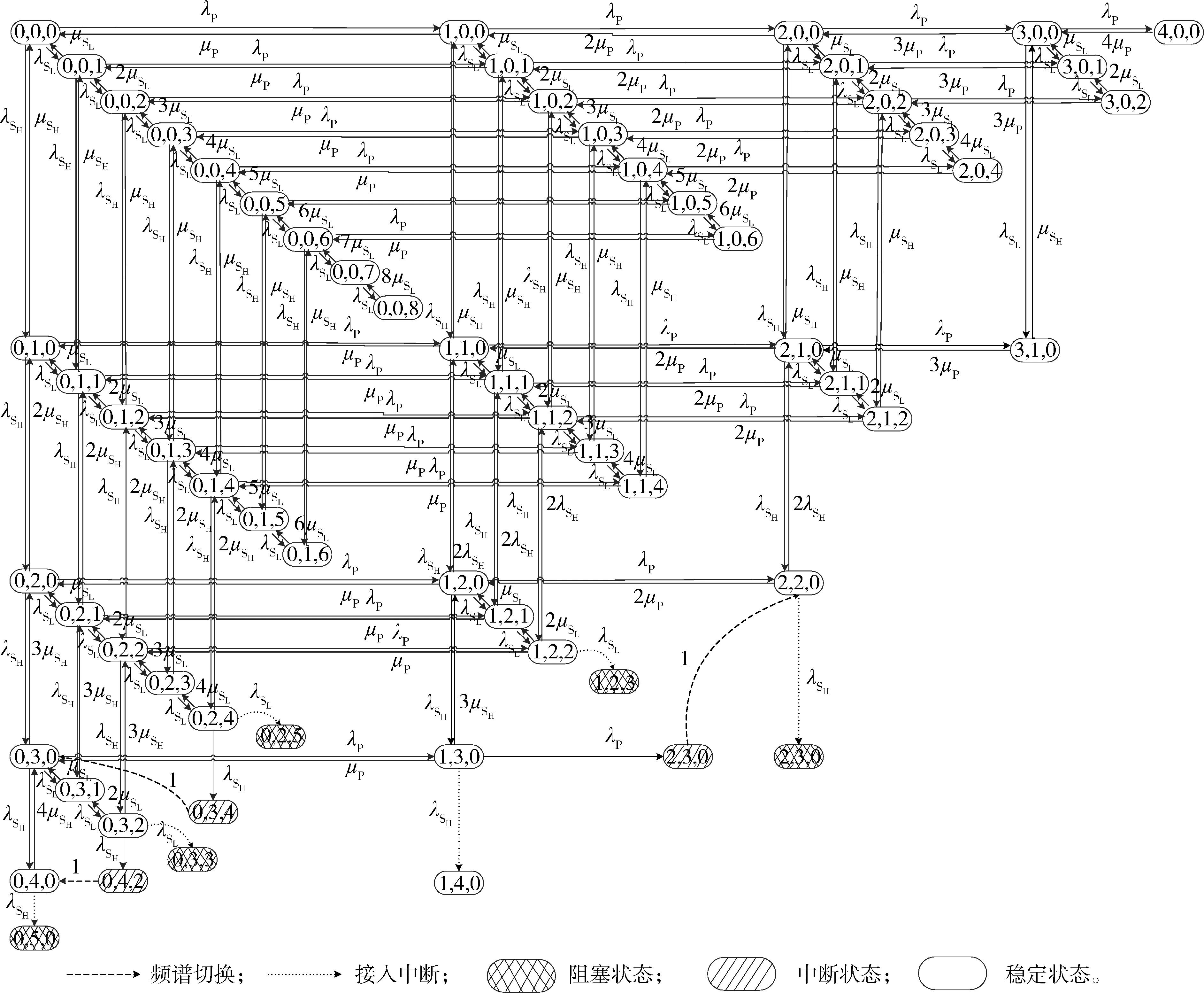
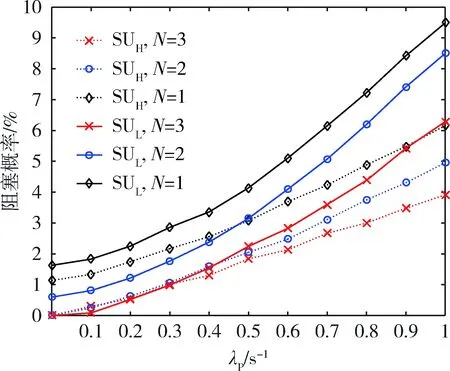
3) 空闲子信道数目与SUL占用的子信道数之和 PU退出信道,其退出速率为iμP,状态转移为(i,j,k)→(i-1,j,k)。 SUH到达信道时,其到达速率为λSH,根据空闲子信道数可分为以下3种情况: 1) 空闲子信道数≥N1, 即iN+(j+1)·N1+kN2≤MN,SUH到达后占用了N1个空闲子信道,状态转移为(i,j,k)→(i,j+1,k)。 2) 空闲子信道数 3) 空闲子信道数与SUL占用的子信道数之和 SUH退出信道,其退出速率为jμSH,状态转移为(i,j,k)→(i,j-1,k)。 SUL到达信道,只有空闲子信道数≥N2这一种情况,即iN+jN1+(k+1)N2≤MN,SUL到达后才可接入信道,状态转移为(i,j,k)→(i,j,k+1),速率为λSL;否则,SUL到达后转到阻塞状态S5。 SUL退出信道,其退出速率为kμSL,状态转移为(i,j,k)→(i,j,k-1)。 综合各用户到达、退出信道的情况,状态转移如图2所示。 图2 状态转移图 令Pi,j,k是平衡状态下传输信道中PU、SUH和SUL在系统中的数量为i、j、k的稳态概率。系统的平衡状态方程为 (λP+λSH+λSL+iμP+jμSH+kμSL)Pi,j,k=λPPi-1,j,k+λSHPi,j-1,k+λSLPi,j,k-1+ (i+1)μPPi+1,j,kIi+1,j,k+(j+1)μSHPi,j+1,kIi,j+1,k+ (k+1)μSLPi,j,k+1Ii,j,k+1, (1) 式中: 则状态集合 Ω= {(i,j,k)0≤i≤M; 0≤j≤⎣N(M-i)/N1」; 0≤k≤⎣[N(M-i)-jN1]/N2」}。 (2) 状态空间总数 。 持续的痛感 C类纤维负责传递由有害物质、高温、压力等产生的信号,但它们传输的速度很慢。这正是为什么瘀伤等疼痛会持续很久的原因。 (3) 状态转移的约束条件是所有状态的稳态概率和为1,即 (4) 当网络中有用户接入信道,然而信道全部被占用或没有足够多的信道数满足新用户的接入时,SUL无法接入,转为阻塞状态。PU不会处于阻塞状态。 当空闲子信道数与SUL占用的子信道数之和 (5) 当空闲子信道 (6) 当网络中有SUH接入信道,SUL空闲信道足够多时,需要切换到可用空闲信道,接入用户处于切换状态。PU不会处于切换状态。 当PU到达时,空闲子信道数与SUL占用的子信道数后之和 α1(i,j,k)=「[N-(MN-iN-jN1)/N1]⎤。 (7) 则SUH的频谱切换概率 (8) 当PU到达时,空闲子信道数与SUH占用的子信道数之和 α2(i,j,k)=「[N-(MN-iN-jN1-kN2)]/N2⎤ ; (9) α3(i,j,k)=「[N1-(MN-iN-jN1-kN2)]/N2⎤。 (10) 则SUL频谱切换概率 (11) 当网络中有SUH接入信道,SUL没有足够多的空闲信道时,SUH接入会导致低优先级用户被迫中断数据传输,从而转入中断状态。PU不会处于中断状态。 空闲子信道数与SUL占用的子信道数之和 β1(i,j,k)=「[N+jN1-(M-i)N]/N1⎤ (12) 个SUH被迫中断数据传输。则SUH的中断概率 (13) 空闲子信道数 β2(i,j,k)=「[N+jN1+kN2-(M-i)N]/N2⎤ (14) 个SUL被迫中断数据传输。 空闲子信道数 β3(i,j,k)=「[N1+jN1+kN2-(M-i)N]/N2⎤ (15) 个SUL被迫中断数据传输。 则SUL的中断概率 (16) 为了分析PU参数对不同优先级SU的影响,笔者设计了不同PU参数下SU接入的性能比较实验。仿真中设置授权信道数目M=4,授权信道分成的子信道数目N为实验变量,分别设置为1、2、3。SUH需要的子信道数目N1=2,SUL需要的子信道数目N2=1。SUH到达信道的速率λSH=0.2 s-1,SUL到达信道的速率λSL=0.2 s-1,PU到达信道的速率λP是因变量,设置为0~1 s-1,间隔为0.1 s-1。PU平均传输时间μP=0.4 s,SUH平均传输时间μSH=0.2 s,SUL平均传输时间μSL=0.2 s。 以(i,j,k)=(4,2,2)为例建立连续马尔科夫链模型,以演示状态转移过程,如图3所示。受篇幅所限,部分阻塞状态和中断状态转移情况以图3左下角所示的状态转换关系为例进行说明。 在以(4,2,2)为例的仿真参数下,连续马尔科夫链模型共有55个稳定状态,由式(1)、(2)得到55个稳态方程,然而所有稳定状态的总到达信道速率与总退出信道速率之和为0,55个方程中任何一个方程都能用其他54个方程表示,也就是有54个线性方程,结合式(4)给定的约束条件,得到以转移概率为参数、稳态概率为未知数的线性方程组,求解线性方程组即可得到稳态概率。 由式(5)、(6)可得到SUH、SUL的阻塞概率,其变化曲线如图4所示。可以看出:随着λP增加,SUH、SUL的阻塞概率均增大,这是因为PU到达得越快,占用信道越多;同时增大N,SU有更多的信道可使用,SUH、SUL的阻塞概率均随N的增大而减小,但增大N需要更先进的调制编码技术来支撑;在同等信道资源下,SUL的阻塞概率及其增大速率均大于SUH,表明信道资源的紧张对SUL造成的影响比SUH更加显著。 由式(8)、(11)可得SUH、SUL的切换概率,其变化曲线分别如图5、6所示。可以看出:随着λP增加,SUH、SUL的切换概率均增大;随着N增大,SUH、SUL的切换概率均减小;在同等信道资源下,SUL的切换概率比SUH约增大了一个数量级,这是因为SUH在PU占用信道时切换信道,而处于被动使用信道的SUL在PU、SUH使用信道时都会切换信道,也表明信道资源的紧张对SUL造成的影响比SUH更加显著。 图3 (4,2,2)连续马尔科夫链模型状态转移过程 图4 SUH、SUL阻塞概率变化曲线 由式(13)、(16)可得SUH、SUL的中断概率,其变化曲线如图7所示。可以看出:随着λP增加,SUH、SUL的中断概率均增大;随着N增大,SUH、SUL的中断概率均减小;在同等信道资源下,SUL的中断概率及其增大速率均大于SUH。由此可知:PU占据信道会使SU通信中断;在同等信道资源下,SUL发生通信中断的可能性大于SUH,且SUH、SUL的中断概率差距不明显。 图5 SUH的切换概率变化曲线 图6 SUL的切换概率变化曲线 笔者在军事应急网络接入现有战术通信骨干网的通信环境下,对SU规定了不同等级的接入信道优先级,利用连续马尔科夫链建立了系统模型,并分别研究了SUH和SUL到达、退出信道的情况。依据模型得到了通信系统中不同等级SU的阻塞概率、切换概率和中断概率,从而得到接入行为中PU的到达速率和授权信道划分子信道数目对SU性能的影响。研究结果为后续军事应急网络的多用户预留信道频谱接入、不同等级优先级用户合作式频谱接入等相关应用方案设计提供了理论支撑。 参考文献: [1] MITOLA J,MAGUIRE G.Cognitive radio:making software radios more personal[J].IEEE personal communications magazine,1999,6(4):13-18. [2] 项亚楠,徐以涛,项楠,等.基于BP神经网络的认知无线电疑似跳转信道预测研究[J].通信技术,2015,48(3):311-317. [3] GÖZÜPEK D,ALAGÖZ F.Genetic algorithm-based scheduling in cognitive radio networks under interference temperature constraints[J].International journal of communication systems,2011,24(2):239-257. [4] YI C,CAI J.Two-stage spectrum sharing with combinatorial auction and stackelberg game in recall-based cognitive radio networks[J].IEEE transactions on communications,2014,62(11):3740-3752. [5] ZHAO Q,TONG L,SWAMI A,et al.Decentralized cognitive MAC for opportunistic spectrum access in ad hoc networks:a POMDP framework[J].IEEE journal on selected areas in communications,2007,25(3):589-600. [6] WANG J W,ADRIMAN R.Analysis of opportunistic spectrum access in cognitive radio networks using hidden Markov model with state prediction[J].Eurasip journal on wireless communications & networking,2015,2015(1):10. [7] MUTHUMEENAKSHI K,RADHA S.A generalized Markovian based framework for dynamic spectrum access in cognitive radios[J].Ksii transactions on internet & information systems,2014,8(5):1532-1553. [8] FAN R,JIANG H.Channel sensing-order setting in cognitive radio networks:a two-user case[J].IEEE transactions on vehicular technology,2009,58(9):4997-5008. [9] SHOKRI-GHADIKOLAEI H,SHEIKHOLESLAMI F,NASIRI-KENARI M.Distributed multiuser sequential channel sensing schemes in multichannel cognitive radio networks[J].IEEE transactions on wireless communications,2013,12(5):2055-2067. [10] ZHU X,SHEN L,YUM T S P.Analysis of cognitive radio spectrum access with optimal channel reservation[J].IEEE communications letters,2007,11(4):304-306.2.2 高优先级认知用户到达、退出信道
2.3 低优先级认知用户到达、退出信道
2.4 连续马尔科夫链模型状态转移
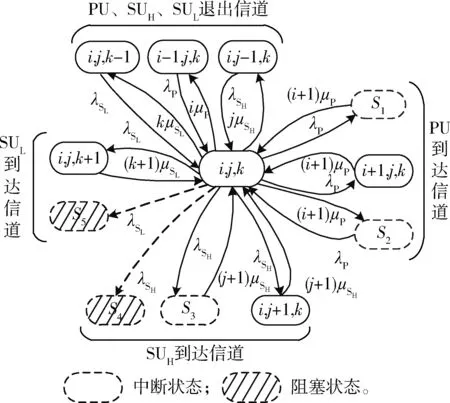
3 性能分析
3.1 阻塞概率
3.2 切换概率
3.3 中断概率
4 仿真实验及结果
4.1 仿真参数设置
4.2 实验计算过程
4.3 实验结果与分析


5 结论
