尼尔基水库控制流域伽玛分布地貌瞬时单位线推导

颜旭光

（嫩江尼尔基水利水电有限责任公司，黑龙江齐齐哈尔161005）

尼尔基水库控制流域伽玛分布地貌瞬时单位线推导

颜旭光

（嫩江尼尔基水利水电有限责任公司，黑龙江齐齐哈尔161005）

本文采用线性特征河长的概念，结合流域地貌特征，根据概念性流域地貌汇流模型的一般理论，以概念性元素“特征河长河段”模拟各级河道的汇流作用，建立了基于线性特征河长河段的伽玛分布地貌瞬时单位线模型。推导出了尼尔基水库控制的四级流域瞬时单位线的表达式，讨论了参数的约束条件和参数的推求方法，并分析了模型参数对瞬时单位线的影响。

地貌瞬时单位线;特征河长河段;伽玛分布;尼尔基水库

0引言

多年来，水文计算都是建立在降雨与径流观测资料分析的基础上，即使引进一些地理因子（如河长、面积、坡度等），也只是用来作为建立某种经验公式的变量。然而，河流是气候的产物，河网的特征集中地反映了一个流域的水文情态，同时，水质点的汇集与流动又受到河网的约束。因此，寻找一种新的途径来确定洪水过程与流域地貌因子之间的必然联系，从而将流域地貌信息转化为水文信息，是水文工作一个大的发展方向，地貌单位线理论正好解决了此问题。

假定一个单位的净雨瞬时地均匀地降在流域上，其每个雨滴在每个河段的运动可用马尔科夫过程来描述，由于这个假定产生了雨滴在每级河段上的滞留时间服从指数分布，忽略坡面汇流时间，就能把各级河流之间的转移概率和初始概率与河网地貌特征联系起来，从而得到雨滴到达出口断面的概率密度函数，即地貌瞬时单位线（GIUH）。

下文以“特征河长河段”的响应函数（其形式等价于统计学中的伽玛分布）作为水质点传播时间的概率密度函数，并结合地貌瞬时单位线理论以及汇流参数之间的关系，从而建立尼尔基水库控制的四级流域的以洪水波的波速和扩散系数为参数的伽玛分布地貌瞬时单位线模型。

1 地貌特征的概念

本文采用Strahler河流分级体系：河流最上游的点称为河源，而最下游的点称为出口，2条支流相交处称为连接点，从河源开始的支流称为一级支流。2条同级河流相交形成高一级河流，当2条不同的河流相交时，其下游河流的级别等于该2条河流中级别较高者，一直延续到流域出口断面。整个河系的级别以最高级河道的级别命名，尼尔基水库控制流域属四级流域。

地貌数据按Horton地貌律统计。

1）河数率：

式中：Ni——第i级河流的数目；RB——分叉率，变化范围3.0～5.0。

2）河长率：

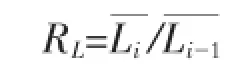
3）面积率：

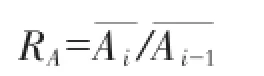
2 概念性元素“特征河长河段”的响应函数

概念性元素“特征河长河段”是建立在圣维南方程基础上的，表示蓄泄系数为k的n个相等线性水库的串联，其响应函数h（t）为

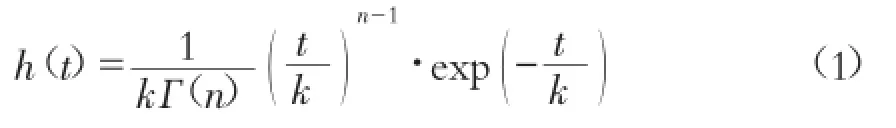
式中：Г（n）为伽玛函数；exp（.）为指数函数。

通过与概率统计学中伽玛分布的密度函数形式对比可知，概念性元素“特征河长河段”的响应函数与伽玛分布的密度函数形式完全相同，用概念性元素“特征河长河段”的响应函数作为水质点传播时间的概率密度函数，不仅具有统计学意义，而且具有水动力学基础。

根据洪水波推移和坦化作用的定义，波速C反映了洪水波的推移作用，扩散系数D反映了洪水波的坦化作用。而文献[1]中“特征河长河段”的参数n，k与河道长度L及波速C和扩散系数D之间存在如下关系：

式（2）表明，“特征河长河段”的参数n，k均与C，D有关，说明参数n，k同时反映了洪水波的推移和坦化作用。

3 模型结构及地貌瞬时单位线推导

3.1 基本概念

状态：水滴在流域上所处的空间位置，指某级坡面或某级河流；路径：由各状态按流域汇流的物理顺序组成的集合，它表明水滴在流达出口断面的过程中按顺序所经历的各种状态；状态转移：水滴由一个状态向另一个状态的转移；状态转移概率：水滴由一个状态向另一个状态转移的可能性大小。

3.2 路径概率

降落在流域上某处的水滴可取不同的路径流到流域出口断面。对于尼尔基水库控制的Ω=4级的流域水滴可取的路径为8条，根据流域汇流的物理过程，随机地降落在流域上的水滴的状态转移遵循如下原则：

1）转移出状态ri的唯一可能是属于ri→cj，i=1，2，…，Ω；

2）转移出状态ci的唯一可能是属于ci→cj（j＞i）；

3）由于定义流域出口断面为收集状态，因此转移出状态cΩ+1是不可能的。

ri表示i级河流的坡面状态，i=1，2，…，Ω；ci表示i级河流状态，i=1，2，…，Ω；cΩ+1表示流域出口断面，称为收集状态；sj表示水滴所取的第j条路径，j=1，2，3，4，…。

若某路径s由状态x1，x2，…，xk按流域汇流的物理顺序集合而成，记做s=＜x1，x2，…，xk＞，则由于状态之间相互独立，故路径概率如下：

其中，x1，x2，…，xk∈｛r1，r2，…，ra，c1，c2，…，ca+1｝

式中：φi——水滴处于初始状态的概率，简称初始概率；pxk-1xk——水滴从状态xk-1转移到状态xk的转移概率，k=2，3，4，…，Ω。

3.3 模型结构及公式推导

图1 四级流域汇流模型结构图

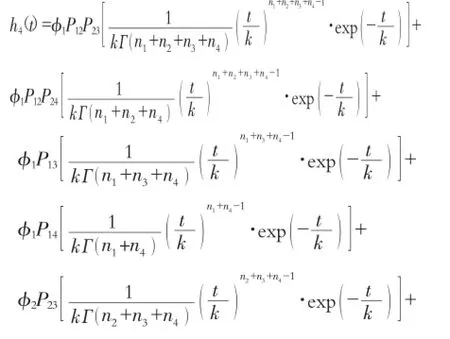
式中初始概率φi，转移概率Pij均可以写成Horton地貌律理论中河长比RL、河流分叉比RB、面积比RA的函数，即

3.4 模型参数估计

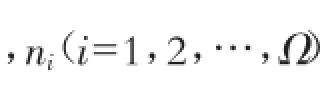
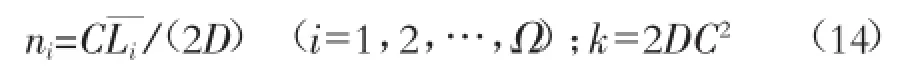
1）目标函数

由实测雨洪资料优选参数时，可以以实测洪水过程线上各离散点的计算值Qi，计与实测值Qi，实之间的离差平方和最小为目标函数，即

式中：n为此次洪水计算时段数。

2）约束条件

①参数C为流域内河流洪水波的平均流速，C值非负；对于给定流域，河道洪水波波速C一般为1.5倍的断面平均流速（u）。因此，波速C满足下列约束条件：

式中：umax为流域出口断面平均流速的最大值。

②参数D，根据其物理概念，D应该为正值。“特征河长河段”参数n大于1，根据式（15），当ni＞1时，D＜CLi/2（i=1，2，…，Ω），由此得到参数D的约束条件为

3）求解方法

由式（16）、（17）和（18）构成了有约束极小值问题，可通过内罚函数法转化为无约束极小值问题来求解。

3.5 模型参数对模型影响

1）参数n和k既反映了洪水波的推移特性、洪水波的坦化特性（均与C和D有关）。但nk只与流速C有关，反映了洪水波的推移特性；n2k只与扩散系数D有关，反映了洪水波的坦化特性。

2）当L，C为定值时，相应线性水库的调蓄能力随之而减弱。

3）当C，D为定值时，瞬时单位线的洪峰流量将减小。

4）当L4，D为定值时，峰现时间将滞后，洪峰流量将减小。

5）当L4，C为定值时，洪峰流量将减小，峰现时间不变。

4 结语

本文以概念性元素“特征河长河段”模拟各级河道的汇流作用，应用地貌单位线理论推导出了尼尔基水库控制的四级流域的伽玛分布地貌瞬时单位线，具有明确的物理基础，参数少，易于求解，对今后尼尔基水库控制流域汇流特性的分析研究具有重要的意义，对流域产汇流模型的建立有重要的理论价值，同时也是尼尔基水库水文预报研究的一个重要方向。

地貌气候瞬时单位线理论发展至今，其理论基础已经得到了认可，但仍有一些问题需要进一步的研究，如水质点滞留时间概率密度函数的合理表达与求解、参数的合理定量等问题。这些问题的解决不仅仅依赖于水文学理论的发展，还与计算机技术的应用和发展有着很大的关系，快捷准确地获取地貌信息会使基于地貌瞬时单位线理论的汇流模型更加准确、应用范围更广。

［1］芮孝芳.水文学原理［M］.北京：中国水利水电出版社，2004.

［2］庄一令鸟，林三益.水文预报［M］.北京：水利电力出版社，1984.

［3］陆桂华.确定性方法推求地貌单位线［J］.河海大学学报，1990（6）：79-84.

［4］葛守西.洪水预报新模型,新技术的研究运用［J］.长江志季刊，2000（3）：26-39.

［5］陈志明.流域地貌瞬时单位线法剖析［J］.水电能源科学，1993（02）.

［6］张正康，赵绥忠.流域地貌瞬时单位线计算洪水探讨［J］.浙江水利科技，1988（4）：11-17.

TV697.1+3

B

1002－0624（2017）04－0046－04

2016-09-02