一种新型抗干扰自适应控制的设计与仿真

王 鑫,陈 欣

(1.南京航空航天大学 自动化学院，南京 211106； 2.中国电子科技集团公司 第三十八研究所，合肥 230088)



【信息科学与控制工程】

一种新型抗干扰自适应控制的设计与仿真

王 鑫1,2,陈 欣1

(1.南京航空航天大学 自动化学院，南京 211106； 2.中国电子科技集团公司 第三十八研究所，合肥 230088)

提出了一种新型的抗干扰模型参考自适应控制的算法，该算法基于关联矩阵、理想匹配模型与LDU分解的抗干扰技术，可用于对各种干扰进行抑制，响应快速，能够确保系统的稳态响应指标和提高系统的瞬态响应性能。选用时变阶跃输入和不匹配干扰，对新型抗干扰自适应控制器与鲁棒伺服LQR控制器进行了对比仿真验证。结果表明,设计的抗干扰控制器对于不匹配扰动具有较强的鲁棒性。

抗干扰控制；LDU分解；模型参考自适应；关联矩阵

在抗干扰技术方面，鲁棒自适应控制算法有较强容忍较大参数误差，结构和不确定干扰的能力，确保系统的跟踪性能。一些优化的自适应方法被设计出来，提高控制器的鲁棒性，文献[1]提出一种死区modification结构的自适应律，这种自适应律当跟踪信号在给定的误差范围内停止自适应计算，然而这种改进会导致在给定区域附近的振荡。文献[2]提出一种σ-modification的自适应律用于改进在小误差区域内的振荡。文献[3]设计了一种e-modification自适应律来取代σ-modification在小的区域内不变的阻尼增益，然而不论是σ-modification 还是e-modification都降低了自适应的响应速度。针对不匹配控制，文献[4]提出了基于前馈的自适应控制器，用于在下沉风干扰情况下的控制。文献[5]提出了一种基于H∞的自适应控制器，用于提高系统的瞬态响应特性。文献[6-9]采用了其他的一些优化算法。然而目前存在的模型参考自适应算法主要针对匹配的干扰设计，或者针对不匹配的干扰设计，只能在一定程度上抑制干扰。

本研究首先分析了匹配和不匹配的干扰，并且针对两种干扰建立了系统的线性模型，然后设计了一种基于LDU分解的抗干扰自适应状态控制器，通过与LQR控制和新提出的模型参考自适应的数值仿真验证和对比分析，验证所提出控制器鲁棒性。

1 问题描述

包含干扰的线性系统如下列方程所示[10]：

(1)

其中，A∈Rn×n,B∈Rn×M,Bd∈Rn×p是未知常数矩阵d(t)=[d1(t),…,dp(t)]T∈Rp是系统的干扰向量。

控制目标是设计控制器v(t)使得系统(1)的输出变量y(t)有界并且能够使得变量逐渐接近于变量ym(t)，其中ym(t)是由如下系统参考模型确定

(2)

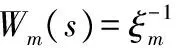
(3)

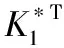
2 控制器的设计

引理1[11]对于任意一个具有非零顺序主子式的矩阵，能够分解为以下唯一形式

Kp=LDU

(4)

其中L是单位下三角矩阵，U是单位上三角矩阵。

引理2[10]对于任何一个满秩的严重有理传递函数G(s)，存在一个下三角多项矩阵ξm(s)，定义为传递函数G(s) 的左关联矩阵，有如下的结构形式

(5)

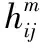
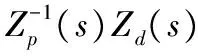
假设1：Gp(s)的零点稳定，即Zp(s)所有零点都在左半平面，并且系统(A,B,C)可稳定且可检测。

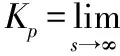
假设3：系统高频增益矩阵Kp的顺序主子式非零并且符号已知。

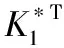
证明:对于系统表达式(1)，输入输出由下列表达式：

(6)

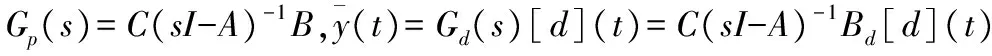
(7)

(8)

(9)

由式(9)可得控制律

(10)

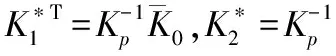
(11)

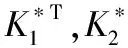
(12)

利用引理LDU分解，不确定性矩阵高频增益Kp可以将式(14)变为如下形式：

(13)

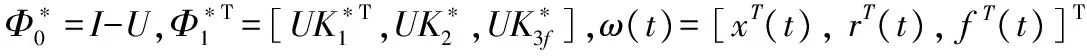
(14)

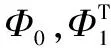
于是通过式(13)，两边同时乘以h(s)IM，可以得到

(15)

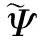
自适应更新律基于误差表达式(15)，采用梯度算法，得到系统自适应律如下：

(16)

(17)

(18)

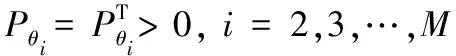
(19)

3 仿真结果

按照设计的抗干扰模型参考自适应控制器与文献[8]中的自适应方法在加入不匹配干扰后的线性飞机模型中进行仿真对比验证，其仿真结果如图1～图4所示。

由图1～2可知，在不匹配干扰的情况下，系统受干扰的响应曲线受到影响，飞机的副翼和方向舵出现抖动，且滚转角和侧滑角的响应不稳定。由图3～4可知，提出的模型参考自适应方法具有较强的抗干扰能力，系统响应满足指令的要求。

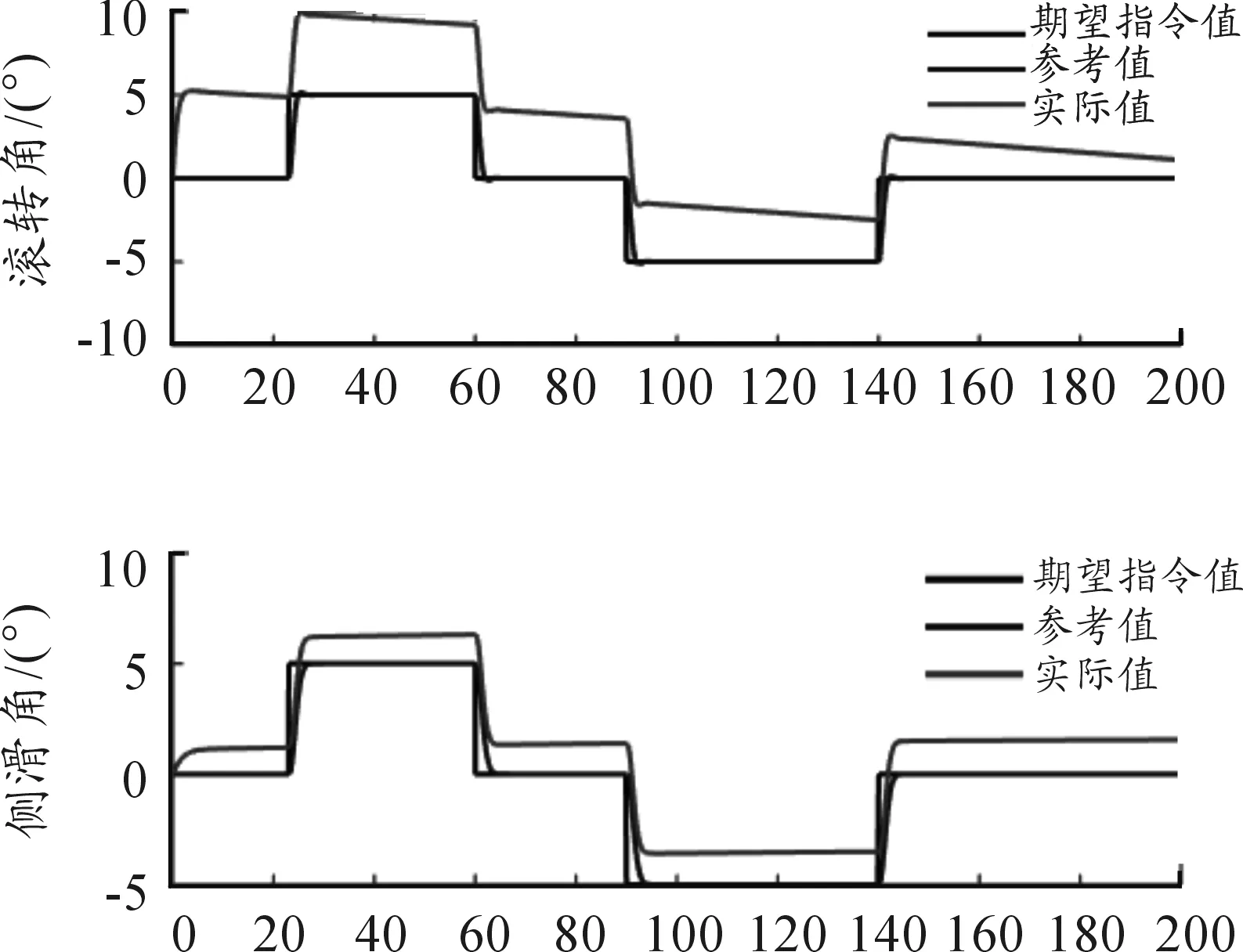
图1 一般自适应方法滚转角和侧滑角响应曲线

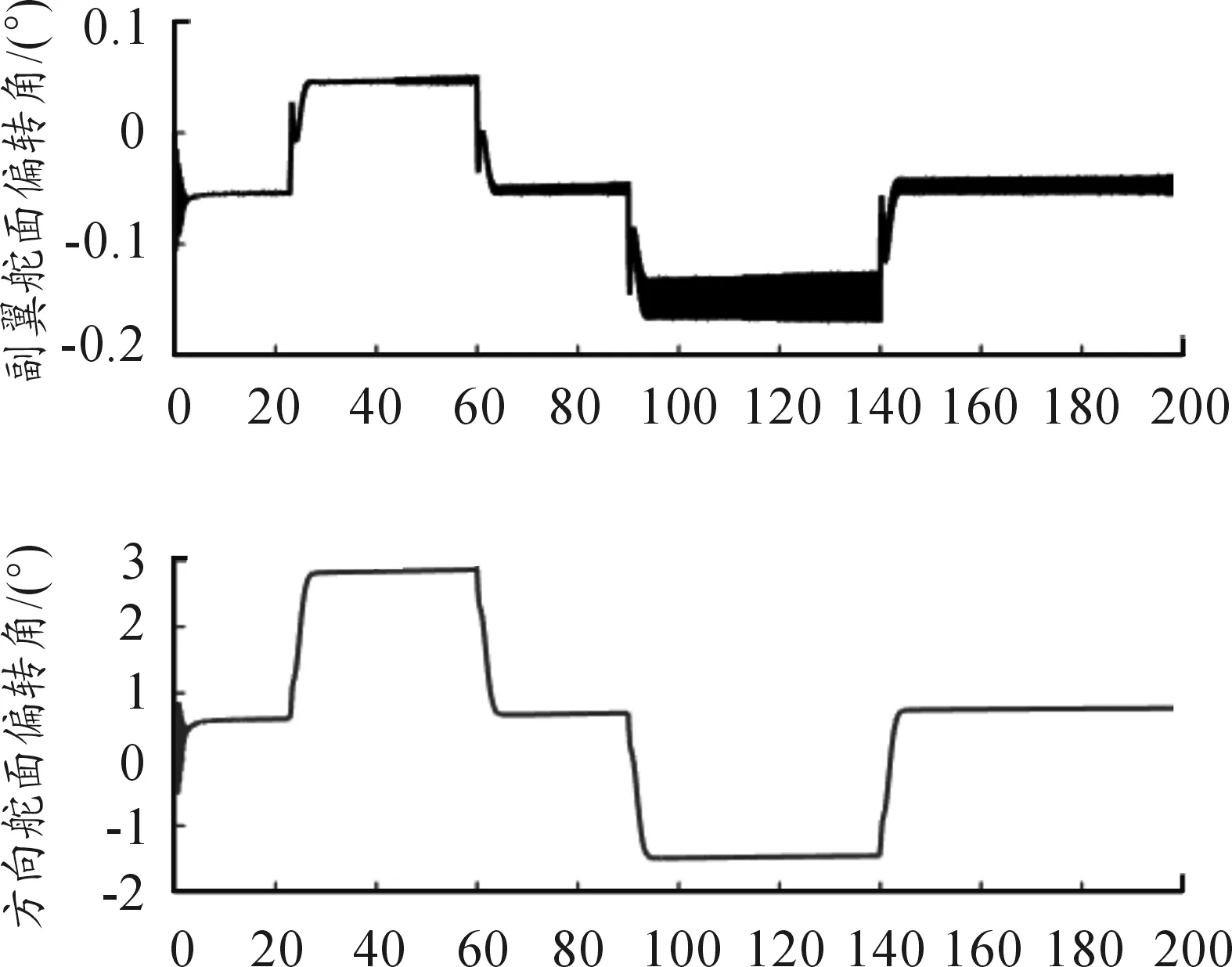
图2 一般自适应方法方向舵和副翼舵输入曲线

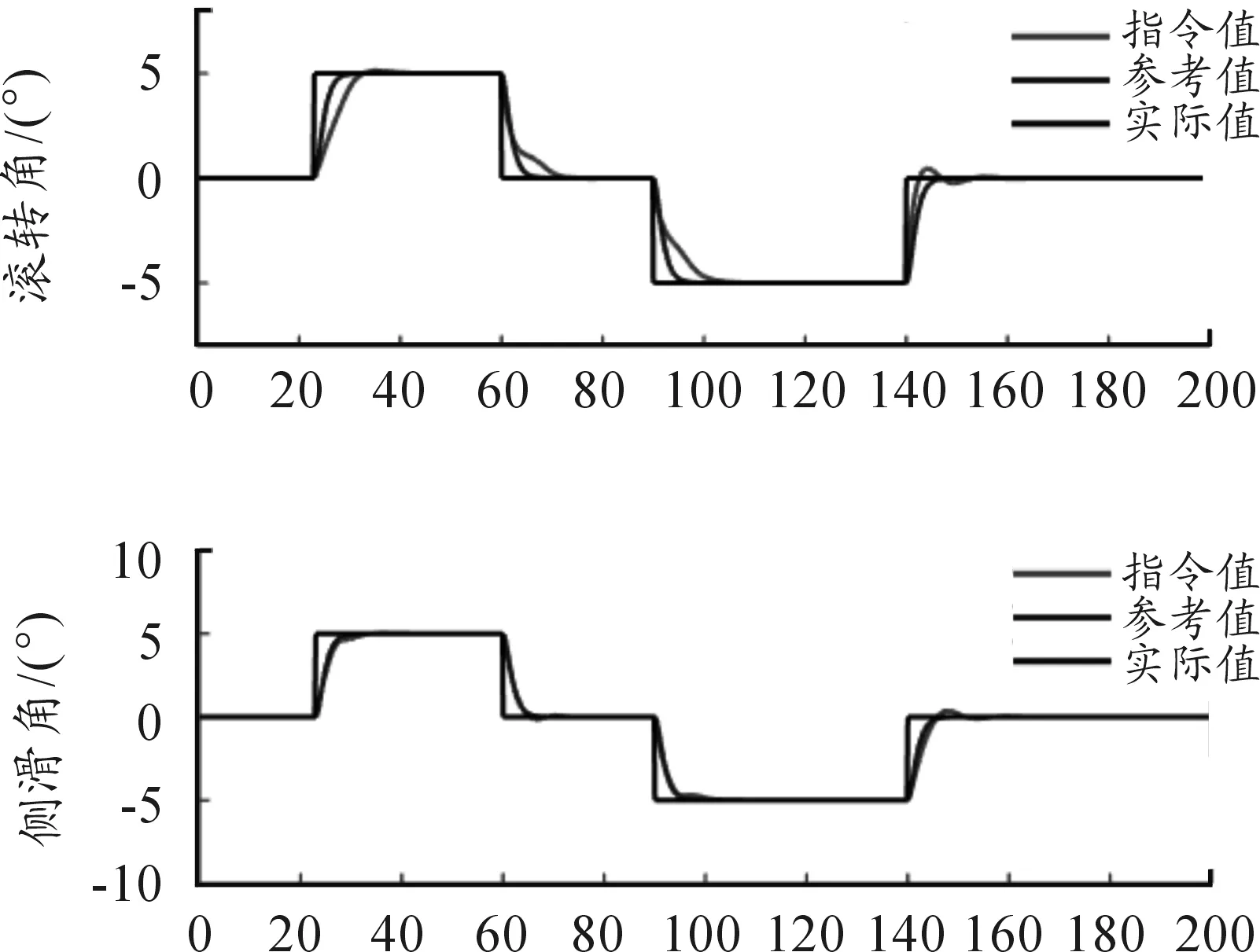
图3 抗干扰自适应控制器响应曲线

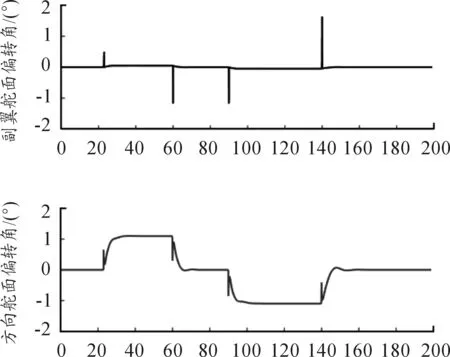
图4 抗干扰自适应控制器方向舵和副翼舵输入曲线

4 结束语

提出了抗干扰模型参考自适应的控制算法，首先建立了干扰系统的线性模型，然后设计了一种基于LDU分解的抗干扰自适应状态控制器，通过与一般模型参考自适应控制和新提出的模型参考自适应的数值仿真验证和对比分析，验证所提出控制器鲁棒性。

[1] PETERSON B B,NARENDRA K S.Bounded error adaptive control[J].IEEE Transactions on Automatic Control,1982,27(3):1161-1168.

[2] NARENDRA K S,ANNASWAMY A M.A new adaptive law for robust adaptation without persistent excitation[J].IEEE Transactions on Automatic Control,1987,32(2):134-145.

[3] IOANNOU P A,TSAKALIS K S.A robust direct adaptive controller[J].IEEE Transactions on Automatic Control,1986,31(11):1033-1043.

[4] GUO XY,BODSON M.Equivalence between adaptive feedforward cancellation and disturbance rejection using the internal model principle [J].International Journal of Adaptive Control and Signal Processing,2010,24(3):211-218.

[5] ZHANG Xiaoyu,HAN Yuntao,TAO Bai,et al.H∞controller design using LMIs for high-speed underwater vehicles in presence of uncertainties and disturbances[J].Ocean Engineering,2015,104(4):359-369.

[6] NHAN T.NGUYEN.Bi-objective optimal control modification adaptive control for systems with input uncertainties[J].IEEE Journal of Automatica Sinica,2014(1):423-434.

[7] NHAN T.NGUYEN.Optimal control modification for robust adaptive control with large adaptive gain[J].Systems & Control Letters,2016,61:485-494.

[8] DYDEK Z T,ANNASWAMY A M,LAVRETSKY E.Adaptive control and the NASA X-15-3 flight revisited[J].IEEE Control Systems,2010,30:32-48.

[9] WIESE D P,ANNASWAMY A M,MUSE J A,et al.Adaptive output feedback based on closed-loop reference models for hypersonic vehicles[J].Journal of Guidance,Control,and Dynamics,2015,38(12):2429-2440.

[10]TAO G.Adaptive Control Design and Analysis[M].Virginia state：John Wiley Sons,2003.

[11]戴华.矩阵论[M].北京：科学出版社,2001.

(责任编辑 杨继森)

Design of a Novel Model Reference Adaptive DisturbanceRejection Controller and Its Simulations

WANG Xin1,2，CHEN Xin1

(1.College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China;2.The No. 38thResearch Institute of China Electronics Technology Group Corporation，Hefei 230088，China)

A novel disturbance rejection model reference adaptive controller was proposed. This controller which can ensure the steady response of the system and improve the transient response performance of the system and it was designed based on interactor matrix, ideal reference model and LDU decomposition to suppress interference. Through simulation and comparison, the results show that the design of adaptive controller has strong robustness to the mismatched disturbance.

disturbance rejection; LDU decomposition; model reference adaptive control; interactor matrix

2016-11-28；

2016-12-15 作者简介：王鑫(1982—)，男，博士研究生，高级工程师，主要从事无人机飞行控制系统研究。

10.11809/scbgxb2017.04.025

王鑫,陈欣.一种新型抗干扰自适应控制的设计与仿真[J].兵器装备工程学报，2017(4):114-117.

format:WANG Xin，CHEN Xin.Design of a Novel Model Reference Adaptive Disturbance Rejection Controller and Its Simulations[J].Journal of Ordnance Equipment Engineering,2017(4):114-117.

V249

A

2096-2304(2017)04-0114-04