基于协方差矩阵重构稳健波束形成算法
2017-04-28陈明建龙国庆黄中瑞
陈明建,龙国庆,黄中瑞
(合肥电子工程学院,合肥 230037)
【专家特稿】
基于协方差矩阵重构稳健波束形成算法
陈明建,龙国庆,黄中瑞
(合肥电子工程学院,合肥 230037)
提出了一种新的基于协方差矩阵重构的稳健算法。该算法基于最小化输出期望信号空间倒谱,利用多项式拟合估计期望信号的导向矢量;从数据协方差矩阵中减去期望信号部分,得到干扰加噪声协方差矩阵,通过修正方法实现对干扰加噪声协方差矩阵的准确估计,解决了低信噪比时由于信号子空间发生缠绕,导致协方差矩阵估计存在较大误差的问题;理论分析与仿真实验表明了该算法的有效性和稳健性。
稳健自适应波束形成;协方差矩阵重构;导向矢量估计;信干噪比
传统自适应波束形成在理想情况下能够获得良好性能[1]。然而实际上训练数据中不可避免包含期望信号,且存在指向误差、阵列幅相误差、信号散射等因素导致导向矢量无法精确获得,期望信号有可能被当成干扰,从而出现信号自相消现象。学者们相继提出了各类稳健自适应算法解决该问题。主要分为以下4类:对角加载算法、特征空间算法、不确定集约束算法以及干扰加噪声协方差矩阵重构算法。对角加载算法是在任意阵列响应误差和小样本数据情况下常用的稳健波束形成算法之一,但如何选择最优的对角加载量,是该算法难题[2-6]。特征空间法是利用期望信号导向矢量在信号和干扰子空间内的投影代替原导向矢量本身,从而减轻信号自相消现象,提高输出信干噪比(SINR)。但该算法在低信噪比时性能下降甚至完全失效[7-9]。针对上述传统方法的不足,基于不确定集约束的稳健波束形成方法相继提出[10-16],如最差性能最优化稳健波束形成(WCPO)、稳健Capon波束形成(RCB)等。由于不确定集稳健算法的阵列接收信号中包含期望信号,在高信噪比时仍然会出现信号相消现象,算法性能受限于导向矢量模约束参数选取,且需要优化算法求解权向量,计算复杂度较高,不利于工程应用。针对上述问题,最近一些学者提出了基于干扰和噪声协方差矩阵重构的稳健算法[17-21],如文献[17]提出基于空间谱的干扰加噪声协方差重构算法,但需要对期望方向外所有空域进行谱估计,计算量较大。文献[18-19]提出一种新的协方差矩阵重构算法,避免积分运算,但该算法只适用于阵列响应模型准确的情况。若阵列存在幅相误差、互耦等时算法性能将下降。文献[20]分析了特征空间法能够获得稳健波束形成的机理,提出了基于信号子空间重构的稳健算法,在任意SNR情况下均能获得稳定性能。文献[21]利用导向矢量的环面不确定集约束,一定程度上解决了任意阵列模型失配导致波束形成性能下降的问题,进一步提高了算法的适用性,但该算法导向矢量计算较为复杂,且若模约束参数选择不当,算法稳健性能改善有限。
针对上述问题,本文提出了一种新的基于干扰加噪声协方差矩阵和导向矢量联合估计的稳健算法,该算法基于最小化期望信号空间倒谱,利用多项式拟合近似求解期望导向矢量和期望信号功率;然后利用接收信号的协方差矩阵中减去期望信号的协方差矩阵,得到干扰加噪声协方差矩阵。同时,为了解决低信噪比时协方差矩阵存在较大估计误差的问题,对干扰加噪声协方差矩阵进行修正,得到了更为准确的协方差矩阵;最后利用Capon算法得到最优权矢量。
1 问题描述
1.1 信号模型
假设由M元各向同性等距线阵组成接收阵列,远场空间的K个相互独立的窄带平面波信号以到达角(DOA)θk入射到该阵列,若x(t)表示M×1维复采样接收数据,则
(1)
(2)
其中Ri+n表示干扰加噪声的协方差矩阵。
利用拉格朗日乘子法可得最优权向量为
(3)
实际中,协方差矩阵通常由多次快拍估计得到,即
(4)
在理想情况下MVDR波束形成器性能理论上能达到最优,但实际应用中存在各种非理想因素(如信号的DOA失配、信源散射、阵元通道误差、阵元位置误差、阵元互藕、短快拍、多径信号干扰等),导致目标信号的导向矢量和数据协方差矩阵估计出现失配,而基于采样矩阵求逆的MVDR形成器对模型失配特别敏感,尤其是当训练样本中出现目标信号时,导致波束形成器的性能严重下降甚至完全失效。
1.2 各类失配对算法性能的影响
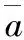
(5)
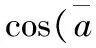
(6)
(7)
则可以推导得到输出SINR为[1]
(8)
其中
(9)
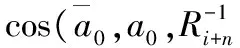

2 典型的稳健自适应算法
2.1 对角加载法
对角加载算法(DL)的核心思想是通过在常规Capon算法的代价函数式中增加一个二次项调整权重向量,即将约束优化问题修改为
(10)
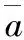
(11)
对角加载算法一定程度上能够克服模型失配导致算法性能下降的问题,但该算法的关键是如何确定最优加载量。对角加载因子γ选择过小或者过大,都无法达到稳健自适应波束形成的目的。
2.2 特征子空间法
基于特征子空间算法是通过将导向矢量投影到信号加干扰子空间,得到新的导向矢量:
(12)
将式(12)代入式(3)可得
(13)
对期望信号进行投影,一方面可以消除噪声子空间扰动带来的影响,另一方面进一步修正期望信号导向矢量,减小误差的影响。但该算法的不足是在低信噪比时或者信源数未知时,由于子空间的缠绕(Subspace Swaps)无法准确获得的信号加干扰的子空间,从而导致波束器的稳健性能下降。
2.3 最差性能最优法

最差性能最优法(WCPO)主要思想是设计权值,使导向矢量在已知的不确定集A内的最差情况下的阵列响应都大于1,即
(14)
式(14)是一个二阶锥优化问题,可以使用内点法求解。最差性能最优算法性能的好坏取决于不确定集的ε取值,这在实际应用中很难准确获得,因此ε取值不当将造成算法性能严重下降。
2.4 协方差矩阵重构法
该算法的主要思想是通过矩阵重构剔除协方差矩阵中期望信号,得到干扰加噪声协方差矩阵估计值,其可以通过空间谱积分得到,即
(15)
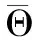
(16)
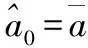
(17)
3 本文算法
3.1 导向矢量估计
式(16)约束优化问题是M维搜索优化问题,算法复杂度较高,不利于工程应用。本文提出了最小化期望信号空间倒谱,利用多项式拟合得到期望信号的导向矢量。算法模型可描述为
(18)
其中Θ=[θ1,θ2]属于期望信号的预估计方向区域,Θ可以通过常规Capon算法在期望信号来波方向波束图的3 dB宽度来确定。
式(18)是一维约束优化问题,可利用多项式拟合思想求解该问题[16],即
(19)
其中Q为多项式阶数,ci为多项式系数。若定义向量c=[c0,c1,…,cQ-1]T, ψ=[1,θ1,…,θQ-1]T,则式(19)可以通过最小二乘算法求解,即
(20)
易得最优解为
(21)
其中
(22)
(23)

(24)

需要说明的是,当信号来波方向估计存在失配时,上述方法可以获得准确的导向矢量;若存在其他阵列误差,如阵列幅相误差、位置误差、阵元互耦等。虽然没法获得准确的导向矢量,但估计的非“真实”导向矢量能够获得最大输出信干噪比。
3.2 干扰加噪声协方差矩阵估计
期望信号的功率可用下式估计得到
(25)
(26)

(27)

(28)

综上所述,本文算法步骤归纳如下:
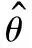
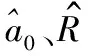
4 仿真实验
考虑10元均匀线阵,阵元间距为半波长;假设空间存在1个目标信号和2个不相关的干扰信号,其中目标的来波方向为5°,信噪比为10 dB;2个干扰信号的来波方向分别为-25° 和45°,干噪比均为30 dB。采样快拍数为100,阵元各通道噪声均为复高斯白噪声。
为了验证本文算法的有效性,分别对固定对角加载算法、特征空间法算法、最差性能最优算法、文献[17,21]算法以及本文算法进行仿真实验,其中对角加载算法对角加载量取10倍白噪声功率;最差性能最优算法参数设置与文献[10]相同。
仿真1 存在指向误差时稳健性能
假定来波方向为0°,即来波方向误差Δθ=5°。图1为存在指向误差时各算法输出SINR随输入SNR变化曲线。图2为存在指向误差时各算法输出SINR随快拍数变化曲线(输入SNR为10 dB)。
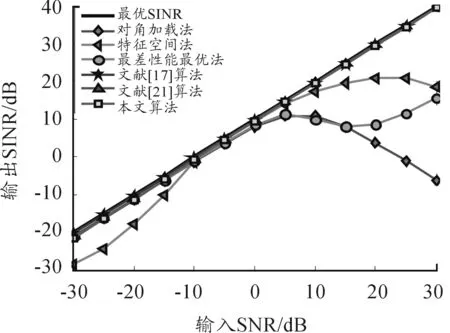
图1 存在指向误差时SINR随SNR变化曲线
由图1可知,当输入SNR较小时,除了特征空间法外,其他稳健算法输出SINR性能大致相同;随着输入SNR逐渐增大时,基于协方差矩阵重构类的稳健算法性能明显优于其他算法。这说明当阵列模型准确已知时,通过重构干扰加噪声的协方差矩阵,消除了期望信号成分,有效避免的各类误差引起的信号自相消,此外,通过对目标信号导向矢量有效估计,保证了目标信号波束增益无损失,进一步提高了算法稳健性能。
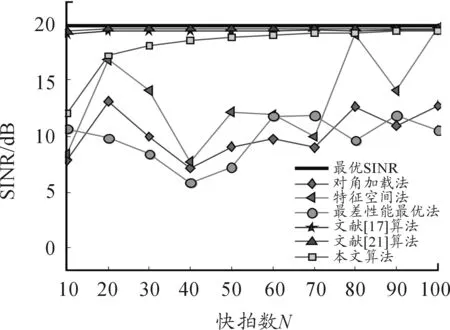
图2 存在指向误差时SINR随快拍数N变化曲线
由图2可知,基于协方差矩阵重构类稳健算法的SINR能够较快收敛于最优值SINR,本文算法收敛速度略慢于文献[17,21]算法,这主要是因为本文算法的协方差矩阵重构依赖于期望信号导向矢量估计,而导向矢量是通过多项式拟合求得,当快拍数较小时,存在一定拟合误差,因此算法的性能有一定的损失,但当快拍数大于80时,算法性能基本收敛到接近最优值。
需要说明的是,本文算法与文献[17,21]算法性能一致,但协方差矩阵无需积分求解,且没有通过优化算法求解导向矢量,而是利用多项式拟合思想求解来波方向,因此算法复杂度较小。
仿真2 存在幅相误差时稳健性能
考虑阵列是未精确校准的,阵列通道的幅度和相位均存在一定误差,其误差均服从高斯分布,其中幅度误差服从CN(1,0.052),相位误差服从CN(0,(0.025π)2),符号CN(a,σ2)表示随机变量服从均值为a、方差为σ2的高斯分布。期望信号来波方向准确已知,其他仿真参数不变。
图3、图4分别为阵列存在幅相误差时各算法SINR随SNR变化曲线、SINR随快拍数变化曲线。
由图3可知,当SNR小于0 dB,本文算法与对角加载、最差性能最优法性能相当,但当SNR大于0 dB,本文算法要优于其他类算法,文献[17]算法性能依赖于阵列模型准确已知,若阵列存在幅相误差、互耦、阵列位置误差等算法性能下降。而文献[21]提出了基于导向矢量不确定集的修正重构算法,虽然一定程度上改善了算法性能,但需要已知导向矢量误差模值,若该系统参数设置不合理,算法性能将受到影响。
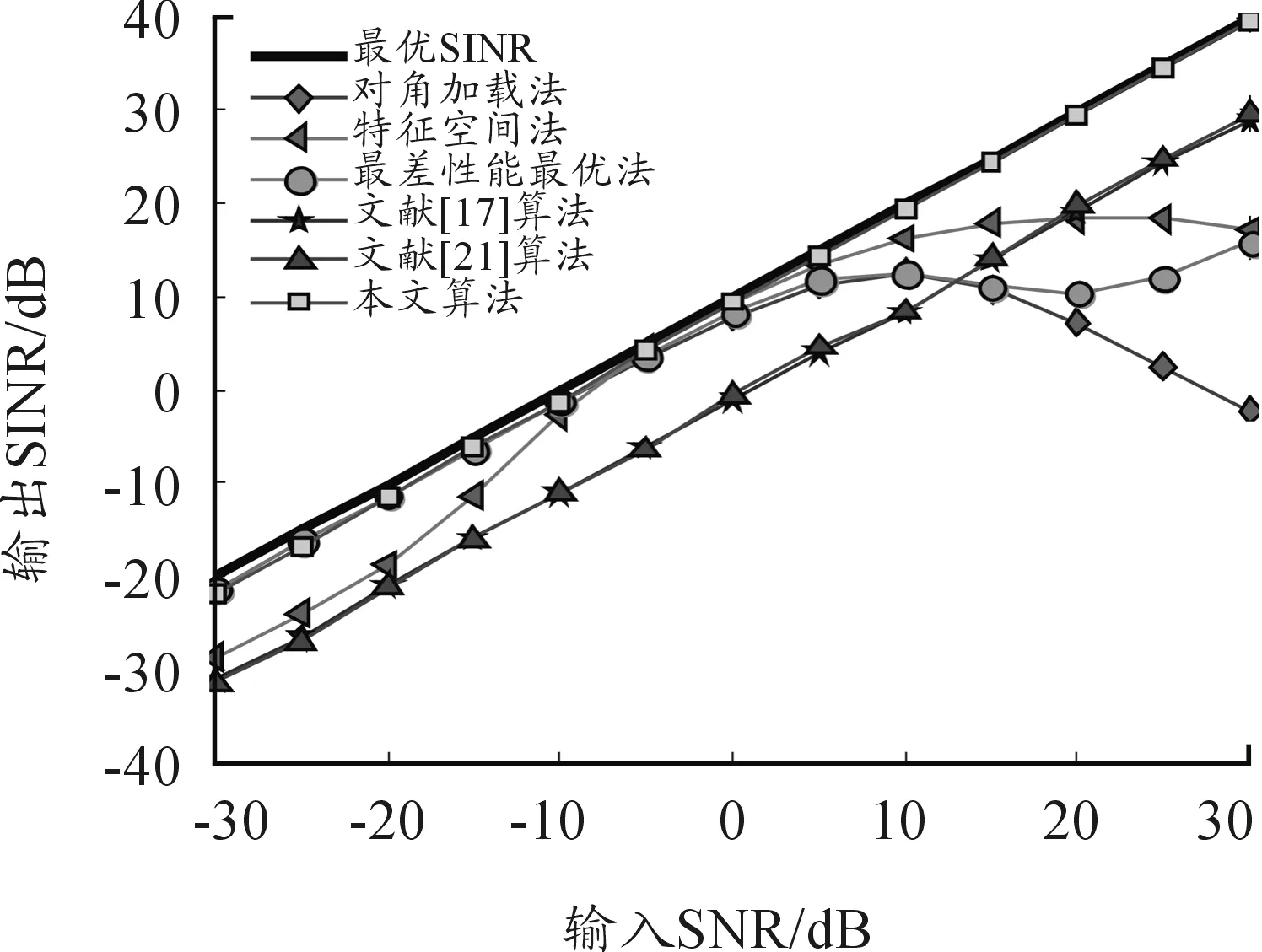
图3 存在幅相误差时SINR随SNR变化曲线
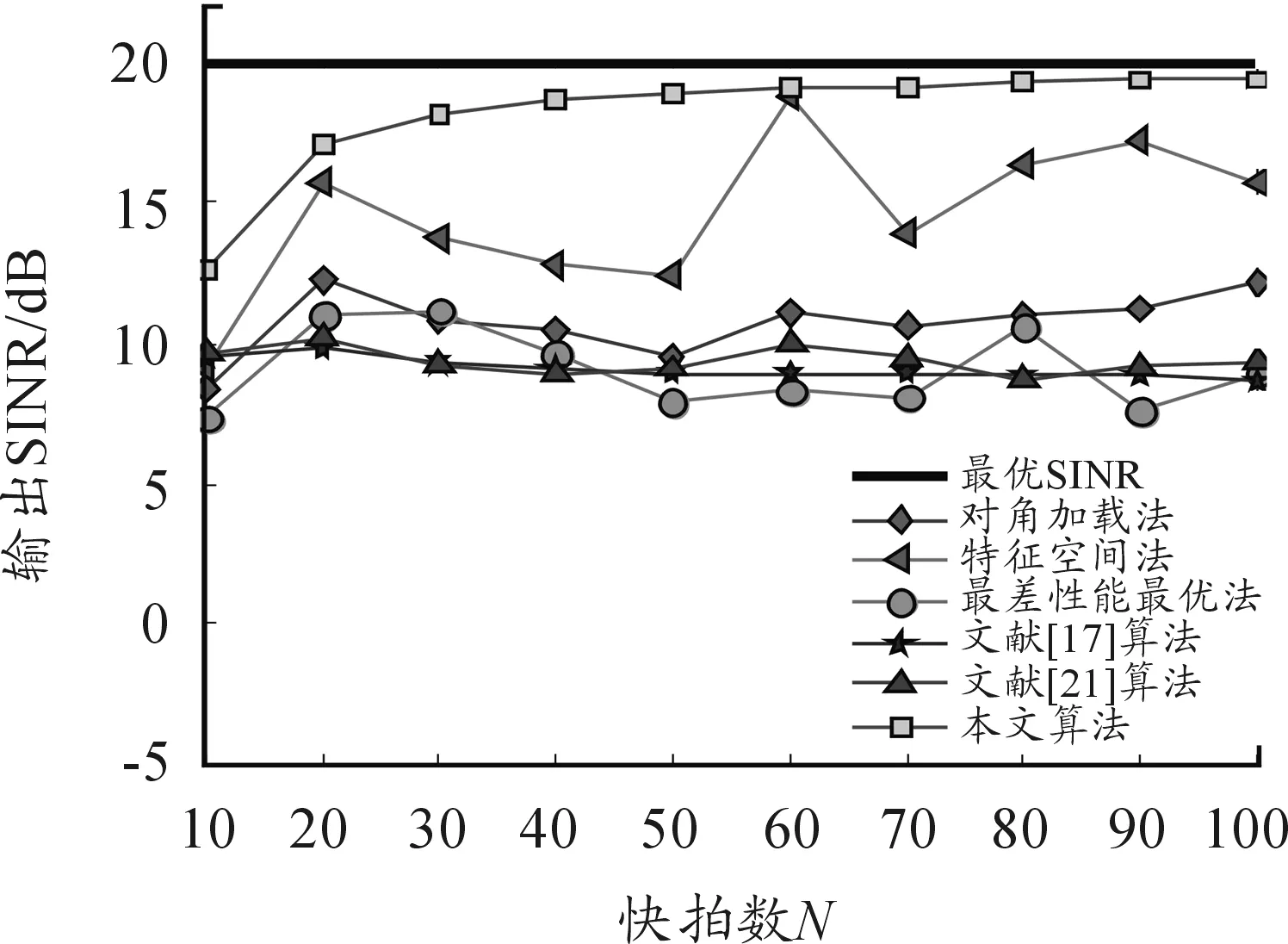
图4 存在幅相误差时SINR随快拍数N变化曲线
由图4可知,本文算法在快拍数接近100时,算法性能渐进收敛于最优值,而其他类稳健算法均无法收敛到最优值。
仿真3 导向矢量存在随机误差时稳健性能
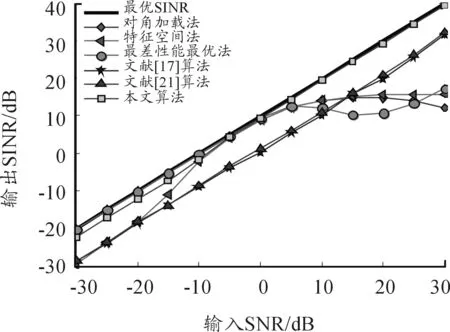
图5 导向矢量存在随机误差时SINR随SNR变化曲线
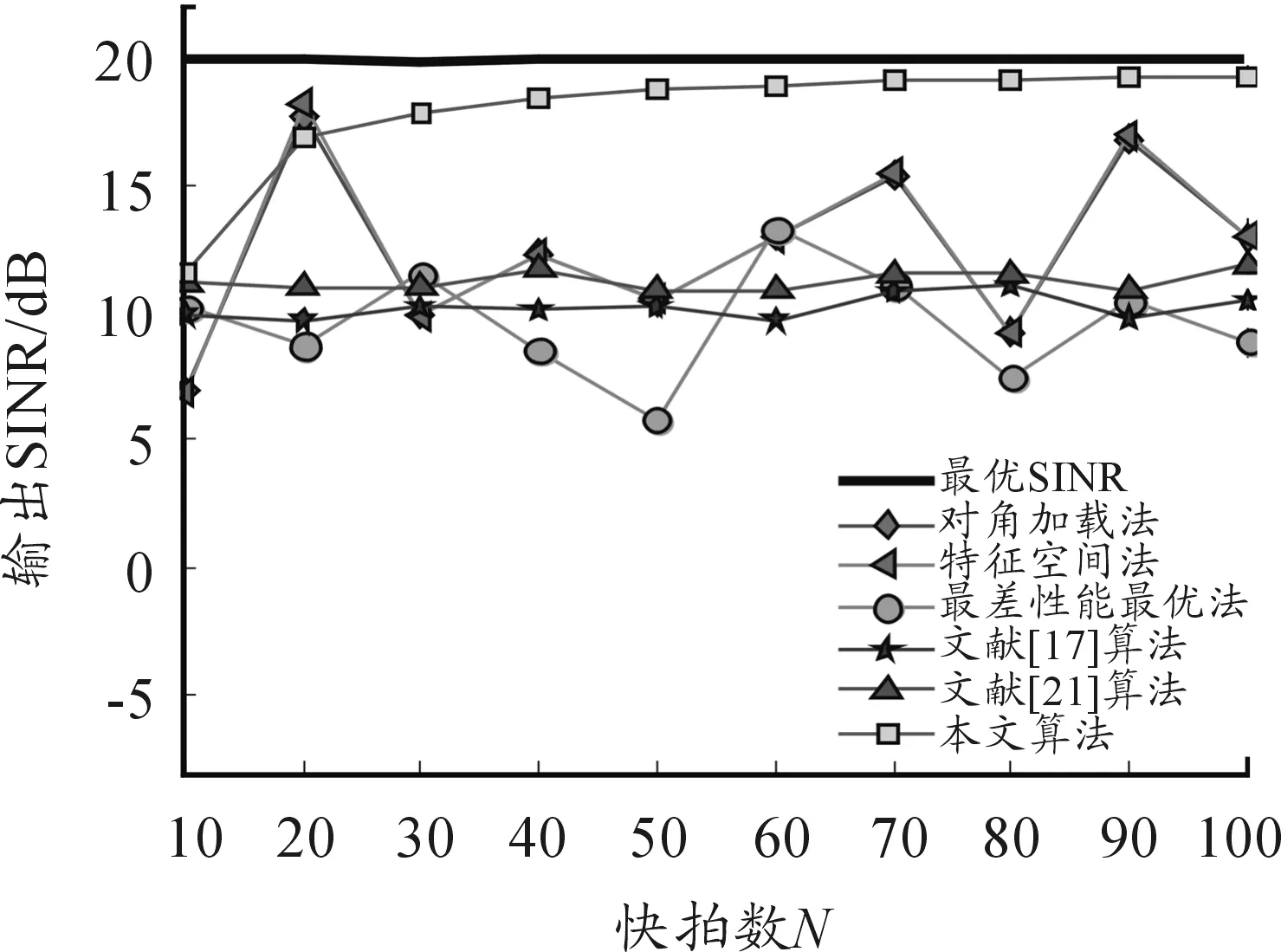
图6 导向矢量存在随机误差时SINR随快拍数N变化曲线
由图5、图6可知,在低信噪比时,本文算法与最差性能最优算法接近,而在高信噪比时,本文算法的优势逐步显现,即使导向矢量存在随机误差,算法性能仍然较优。
仿真实验4 导向矢量存在相干局部散射时稳健性能
从图7、图8可知基于协方差矩阵重构算法的性能明显优于其他算法,随着输出SNR增大,该类算法的干扰抑制能力优势更加明显,SINR能够较快收敛于最优值,且本文算法性能略优于文献[17,21]的重构稳健算法。
综上所述:本文提出基于协方差矩阵重构的稳健算法,在导向矢量存在任意失配时,阵列输出SINR均能够收敛于最优值,且算法复杂度较低,便于工程实现。

图7 存在相干散射时SINR随SNR变化曲线

图8 存在相干散射时SINR随快拍数N变化曲线
5 结束语
针对标准Capon波束形成器存在阵列模型失配时性能下降的问题,本文提出了一种基于干扰加噪声协方差矩阵重构的稳健波束形成算法。该算法利用多项式拟合方法得到导向矢量估计,再根据数据协方差矩阵特征分解重构得到的干扰加噪声协方差矩阵。该算法的主要优点:无需阵列失配程度的先验信息或经验参数的设置,且适合于任意阵列失配情况;当存在导向矢量误差和局部散射等情况时,仍能保证在较大信噪比范围内SINR性能均接近理论最优;算法求解无需任何优化算法,减小了计算量,有利于工程实现。
[1] VANTREES H L.Optimum Array Processing.Part IV of Detection,Estimation,And Modulation Theory[M].Hoboken,NJ,USA:Wiley,2002.
[2] LASEETHA T,SUKANESH R.A Novel Robust Adaptive Beamformer using Diagonal Loading[J].International Journal of Computer Application,2011,19(5):35-40.
[3] 宋海岩,朴胜春,秦进平.基于矢量最优化的稳健波束形成[J].兵工学报,2012,33(10):1222-1229.
[4] SEL E N Y,ABRAHAMSSON R,STOICA P.Automatic Robust Adaptive Beamforming via Ridge Regression[J].Signal Processing.2008,88(1):33-49.
[5] DU L,LI J,STOICA P.Fully Automatic Computation of Diagonal Loading Levels for Robust Adaptive Beamforming[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(1):449-458.
[6] DU L,YARDIBI T,LI J,et al.Review of User Parameter-Free Robust Adaptive Beamforming Algorithms[J].Digital Signal Processing,2009,19(4):567-582.
[7] FELDMAN D D,GRIFFITHS L J.A Projection Approach for Robust Adaptive Beamforming[J].IEEE Transactions on Signal Processing,1994,42(4):867-876.
[8] FELDMAN D D.An Analysis of the Projection Method for Robust Adaptive Beamforming[J].IEEE Transactions on Antennas and Propagation,1996,44(7):1023-1030.
[9] LI J,STOICA P,WANG Z.Doubly Constrained Robust Capon Beamformer[J].IEEE Transactions on Signal Processing,2004,52(9):2407-2423.
[10]HUANG F,SHENG W,MA X.Modified Projection Approach for Robust Adaptive Array Beamforming[J].Signal Processing,2012,92(7):1758-1763.
[11]金伟,刘浩淼,张峰干.基于矩阵重构的多径接收鲁棒波束形成算法[J].兵器装备工程学报,2016,37(8):151-154.
[12]VOROBYOV S A,GERSHMAN A B,LUO Z Q.Robust Adaptive Beamforming using Worst-Case Performance Optimization:A Solution to the Signal Mismatch Problem[J].IEEE Transactions on Signal Processing,2003,51(2):313-324.
[13]VOROBYOV S A,CHEN H,GERSHMAN A B.On the Relationship between Robust Minimum Variance Beamformers with Probabilistic and Worst-Case Distortionless Response Constraints[J].IEEE Transactions on Signal Processing,2008,56(11):5719-5724.
[14]LI J,STOICA P,WANG Z.On Robust Capon Beamforming and Diagonal Loading[J].IEEE Transactions on Signal Processing,2003,51(7):1702-1715.
[15]HASSANIEN A,VOROBYOV S A,WONG K M.Robust Adaptive Beamforming Using Sequential Quadratic Programming:An Iterative Solution to the Mismatch Problem[J].IEEE Signal Processing Letters。2008,15:733-736.
[16]KHABBAZIBASMENJ A,VOROBYOV S A,HASSANIEN A.Robust Adaptive Beamforming based on Steering Vector Estimation with as little as possible prior Information[J].IEEE Transactions on Signal Processing,2012,60(6):2974-2987.
[17]GU Y,LESHEM A.Robust Adaptive Beamforming based on Interference Covariance Matrix Reconstruction and Steering Vector Estimation[J].IEEE Transactions on Signal Processing,2012,60(7):3881-3885.
[18]ZHANG Z,LIU W,LENG W,et al.Interference-plus-noise Covariance Matrix Reconstruction via Spatial Power Spectrum Sampling for Robust Adaptive Beamforming[J].IEEE Signal Processing Letters,2016,23(1):121-125.
[19]WANG Y,BAO Q,CHEN Z.Robust Adaptive Beamforming using IAA based Interference-Plus-Noise Covariance Matrix Reconstruction[J].Electronics Letters,2016,52(13):1185-1186.
[20]MOSTAFA R,MOHAMMAD H B.Robust and Rapid Converging Adaptive Beamforming via a Subspace Method for the Signal-Plus-Interferences Covariance Matrix Estimation[J].IET Signal Processing,2014,8(5):507-520.
[21]HUANG L,ZHANG J,XU X,et al.Robust Adaptive Beamforming with a Novel Interference-Plus-Noise Covariance Matrix Reconstruction Method[J].IEEE Transactions on Signal Processing,2015,63(7):1643-1650.
(责任编辑 周江川)
Robust Adaptive Beamforming AlgorithmBased Interference-Plus-Noise Covariance Matrix Reconstruction
CHEN Ming-jian, LONG Guo-qing, HUANG Zhong-rui
(Electronic Engineering Institute, Hefei 230037, China)
A novel robust algorithm was proposed. In contrast to previous works, the true desired signal steering vector was estimated by solving an optimization problem, and a computationally efficient steering vector estimator has been proposed by polynomial function. The interference-plus noise covariance matrix can be reconstruction by subtracting the desired signal component from the sample covariance matrix. However, when the desired signal presented in the training data is weak, the signal subspace will suffer from the high probability of subspace swap, and as a result, the desired power associated with desired signal will deviate from its true value severely. To prevent the absence of the desired signal steering vector in the estimated signal-plus-interferences subspace, we defined the modified interference-plus noise covariance matrix. The main advantage is that the proposed algorithm is robust against unknown arbitrary type mismatches. Theoretical analysis and simulation results demonstrate the effectiveness and robustness of the proposed algorithm.
robust adaptive beamforming; covariance matrix reconstruction; steering vector estimation; signal to interference plus noise ratio
2016-11-18;
2016-12-15
安徽省自然科学
基金项目(1608085QF140)
陈明建(1983—),男,本刊审稿专家,博士,讲师,主要从事光学工程与电子技术研究。
10.11809/scbgxb2017.04.001
陈明建,龙国庆,黄中瑞.基于协方差矩阵重构稳健波束形成算法[J].兵器装备工程学报,2017(4):1-7.
format:CHEN Ming-jian, LONG Guo-qing, HUANG Zhong-rui.Robust Adaptive Beamforming Algorithm Based Interference-Plus-Noise Covariance Matrix Reconstruction[J].Journal of Ordnance Equipment Engineering,2017(4):1-7.
TN911.7
A
2096-2304(2017)04-0001-07
