汽车刮水器气动升力的风洞试验及数值研究
2017-04-28谷正气丰成杰张启东
谭 鹏, 谷正气,2,*, 陈 阵, 丰成杰, 张启东
(1. 湖南大学 汽车车身先进设计制造国家重点实验室, 湖南 长沙 410082;2. 湖南工业大学, 湖南 株洲 412007)
汽车刮水器气动升力的风洞试验及数值研究
谭 鹏1, 谷正气1,2,*, 陈 阵1, 丰成杰1, 张启东1
(1. 湖南大学 汽车车身先进设计制造国家重点实验室, 湖南 长沙 410082;2. 湖南工业大学, 湖南 株洲 412007)
目前国内外有关汽车刮水器气动升力的研究仅局限于静态转角的稳态数值计算,且尚无相关验证性的试验结果。对此设计和完成了刮水器静态转角的验证性风洞试验,采用多点测试方法测得了四种刮水器在不同风速和转角下的稳态气动升力,辅以稳态数值计算分析了刮水器气动升力产生与变化机理,同时以测试结果验证了相关数值计算方法真实可靠。此外提出了一种新型动网格策略—动网格域盒,结合动网格域盒与用户自定义函数UDF计算分析了刮水器动态转角的瞬态气动升力。研究结果表明,气动升力对刮水器稳定性的影响不容忽视,且在某一特定风速及转角下存在最大值;刮水器上行的气动升力明显小于稳态值,下行的气动升力明显大于稳态值。
刮水器;气动升力;风洞试验;动网格域盒
0 引 言
汽车在雨天行驶时刮水器受来流作用产生的气动升力影响,使其与前风窗贴合性减弱,刮刷效果降低,影响驾驶员视野,从而易引发交通事故。一般解决方法是根据经验增加预压力,此方法虽可维持刮水器的下压力,但刮水器气动升力会随着车速改变而变化,气动升力较小时,过大的预压力会加大刮水器与玻璃间的摩擦力,增加电机负载,此外摩擦力过大,易刮损挡风玻璃,刮水器寿命也会降低。最佳解决方案是研究刮水器的气动特性[1-4],从空气动力学角度正向设计,整体上降低刮水器的气动升力。
国内外学者利用数值计算方法对刮水器的气动特性已做了一定的研究,如基于刮水器的二维模型,探索刮水器刮臂形状、尺寸、位置以及开孔等因素对其气动特性的影响[5];对高速列车的刮水器在三个特殊位置的气动特性进行了对比分析[6];对主、副刮水器处于不同刮刷角度时的稳态升力进行分析[7-8];以及提出一种加装扰流器和翅片的改进方案,并分析刮水器各个功能部件的气动力[9]等。然而,这些研究都只局限于刮水器静态角度的稳态气动升力,不同文献的计算结果相差也较大,而且目前针对汽车刮水器气动升力的试验研究尚处于空白阶段,前人的数值研究结果并未设计相关试验以验证其准确性。
对此本文完成了国内外首例刮水器气动升力测试风洞试验,辅以稳态数值计算探索了刮水器气动升力的产生机理以及在不同风速、不同转角下的变化规律。此外提出了一种适用于复杂边界大幅度运动模拟的新型动网格策略,即动网格域盒。并结合动网格域盒与用户自定义函数(UDF),真实的模拟了汽车刮水器的工作状态,在此前提下对其动态转角的瞬态气动升力进行了探讨。本文旨在为汽车刮水器提供合理的气动升力特性分析与评价方法,以及正向设计的理论依据。
1 汽车刮水器风洞试验
1.1 刮水器试验模型
刮水器气动升力测试试验在湖南大学HD-2闭式回流风洞进行。刮水器的尺寸以及升力数量级较小,在试验过程中,为保证测量精度,避免不确定因素造成更多的误差,采用刮水器实物进行试验。如图1从上至下依次为无骨刮水器、A型三段刮水器、B型三段刮水器、有骨刮水器,长度均为60 cm。
同时为减小阻塞比,设计了用于只安装主刮水器的简化类汽车车头模型,以模拟刮水器的实际工作环境,图2为刮水器安装在类汽车车头模型上。

图1 用于试验的刮水器Fig.1 Wipers of test

图2 刮水器升力测试风洞试验Fig.2 Wind tunnel test of wiper
1.2 气动升力测试方案设计
汽车气动力的测试通常依靠测力天平,对于刮水器气动升力的测量,存在测量空间太小的问题,使得天平布置困难、对流场影响较大以及不适应多角度测量,即使可行,也必须对刮水器模型和挡风玻璃模型做特殊加工,使得试验成本大幅增加。在本试验中,采用了MFF多点薄膜压力测试系统,如图3,薄膜传感器厚度仅为0.2 mm,误差为0.2 N。


图3 MEF薄膜压力测试系统与传感器布置Fig.3 MEF system and the arrangement of the sensors
刮水器刮片胶条与挡风玻璃之间是面接触,若采用多点压力测试系统,需将面接触转变为点接触。对此设计了具体测试方案:
1) 卸除刮水器上的橡胶条,采用与之外形相同的刚性钢条替换,使之在预压力的作用下不会发生形变;
2) 在压力传感器的感压区域固定0.8 mm厚的垫片,使得试验用的传感器总厚度为1 mm;
3) 如图3在刮水器与挡风玻璃之间均匀布置3个压力传感器,各传感器的压力值之和即为总下压力,而未布置传感器的位置则留有微小间隙,均控制在1 mm左右,既保证了点接触形式,又不会对流场造成太大的影响;
4) 分别测试有风作用和无风作用时的下压力,两者之差即为在该风速下由于气流作用刮水器产生的气动升力值。此试验方案能更方便更准确的测得刮水器的气动升力,同时节省了大量试验成本。
1.3 试验工况设置与结果分析
为获取升力的变化规律,需要对刮水器进行多个角度、多个速度的气动升力测量。试验中单个刮水器的试验工况为: 取0°、15°、30°、45°、60°、75°、90°等7个刮刷角度进行试验,测试风速分别为0 m/s、15 m/s、18 m/s、21 m/s、24 m/s、27 m/s、30 m/s,四个刮水器共196个工况。
考虑到壁面对测试的影响,需要对试验结果进行相似性修正,然后运用interp2插值方法将风洞试验结果拟合成连续数据,针对拟合结果中各刮水器峰值处对应的工况再次进行试验,验证了峰值大小和出现位置的正确性。图4为四个刮水器气动升力值与风速、转角之间的关系图。可以看出四个刮水器的气动升力变化规律总体上趋于一致,主要有两个规律:1) 四个刮水器气动升力的峰值出现在大致相同位置,即风速在19 m/s附近,转角在44°附近的位置;2) 如果转角一定,升力与风速的关系是随风速的增大呈先增大后减小的趋势。
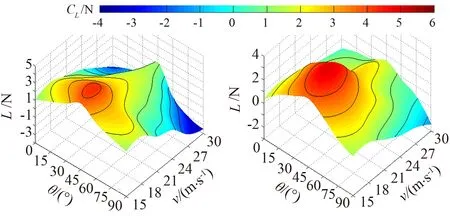
(a) 无骨刮水器 (b) A型三段刮水器
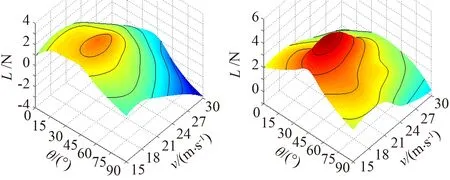
(c) B型三段刮水器 (d)有骨刮水器
其中气动性能最佳的是B型三段刮水器,最大升力为3.533 N,并且在峰值附近升力变化较为平缓,风速增大时,升力以较快的速度减小,最小达到-3.688 N,如图4(c);气动性能最差的是有骨刮水器,最大升力为5.631 N,升力平均值偏高,最小值为-0.563 N,如图4(d)。无骨刮水器与A型三段刮水器的气动性能介于前两者之间,其中无骨刮水器最大升力为4.289 N,最小升力为-3.495 N,峰值附近的升力变化较为平稳,A型三段刮水器的最大升力为4.942 N,最小升力为-1.424 N,峰值附近变化幅度较大,如图4(a-b)。由此可见,刮水器气动升力水平受其外型影响,无骨和B型三段刮水器迎风面具有尺寸大而深的凹槽能有效减小气动升力。
此外,在无风时测得的刮水器预压力为8.211 N,由于气动升力的影响,四种刮水器的下压力最小可低至2.58 N,仅为预压力的31.4%,根据QC/T 44-2009标准[10]可知,对于60 cm刮水器允许的最小下压力为5.4 N。足见气动升力的产生严重影响刮水器的稳定性。
试验中由于设备的精度问题会对结果造成误差,但是误差存在于小数点后一位,对刮水器气动升力的整体变化规律的捕捉不会产生影响。
通过风洞试验发现了刮水器气动升力的变化规律,然而对于刮水器气动升力产生与变化机理的研究难以通过试验来实现,所以下文采用数值方法做进一步的研究。
2 气动升力产生与变化机理分析
2.1 刮水器数值模型建立
建立四个刮水器的1∶1数值模型。对尺寸在1 mm以下的细节进行了简化处理,比如铰接螺钉、橡胶条上的凹槽、一些刮水片支架边缘倒圆等微小特征。这样既保证了较高的网格质量,使计算结果有效,又能提高计算效率。如图5为四种刮水器的三维模型。
同时建立与试验中一致的类汽车车头模型以模拟刮水器的工作环境。如图6为刮水器与类汽车车头模型。

图5 四种刮水器数值模型Fig.5 Numerical model of the wipers
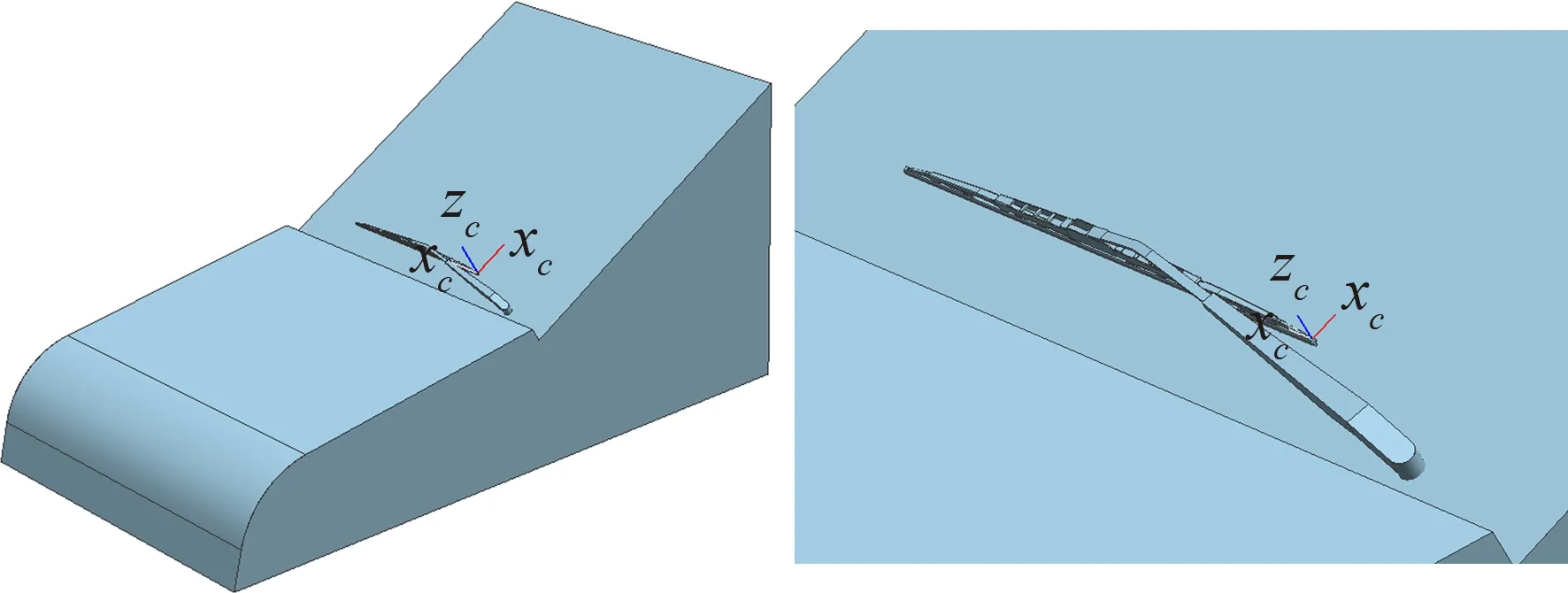
图6 刮水器仿真模型Fig.6 Simulation model of the wiper
2.2 网格划分与边界条件设置
计算域为根据HD-2风洞试验段而建立的长方体域,宽3 m,高2.5 m,长17 m。由于刮水器曲面复杂且结构较小,为方便网格生成,采用四面体与三棱柱非结构网格。在刮水器附近和挡风玻璃表面进行网格加密处理,这样既能保证计算精度又能提高计算效率。划分后计算域网格总数为780万,如图7所示。
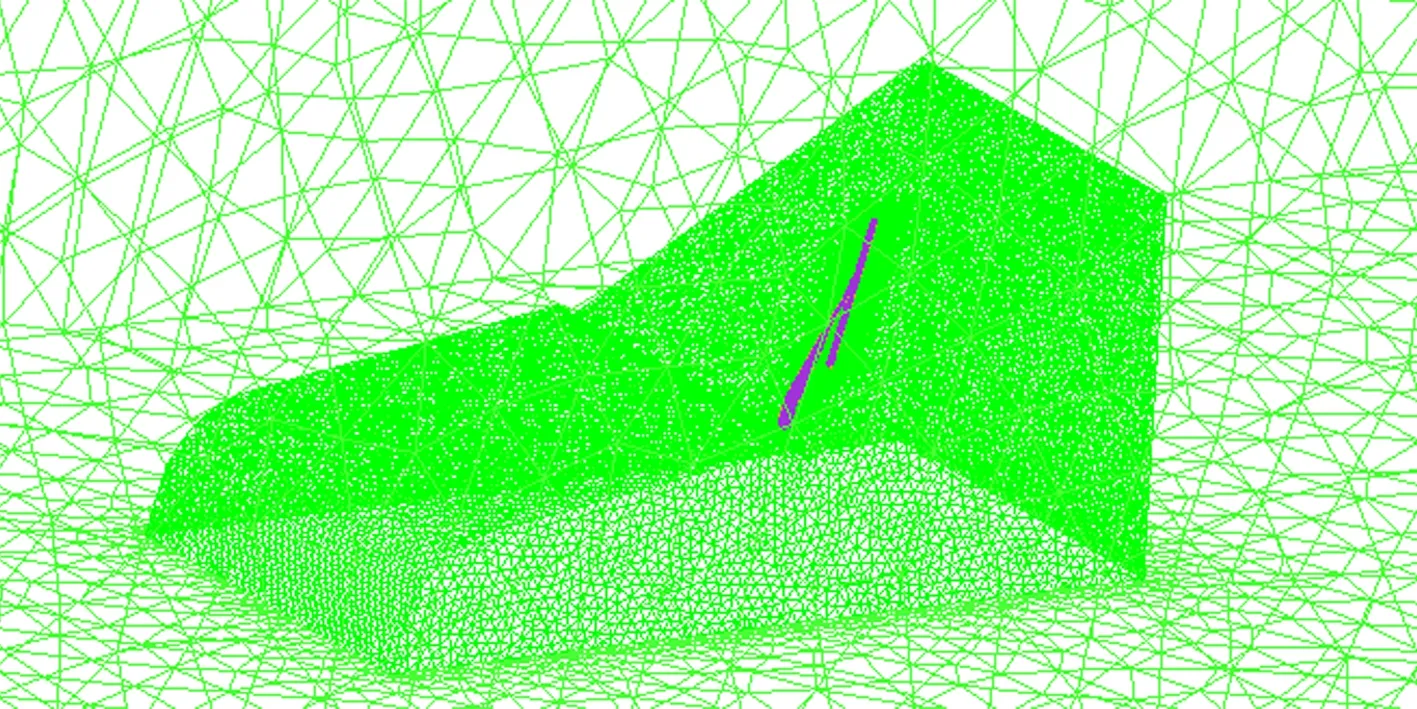
图7 计算域网格Fig.7 Mesh of model
刮水器稳态气动升力数值计算的目的是研究试验所得升力变化规律的机理,无需再进行全工况仿真。根据风洞试验结果,针对单个刮水器设置如下两个工况:1) 转角设置为45°,风速分别设置为15 m/s、18 m/s、21 m/s、24 m/s、27 m/s、30 m/s ;2) 风速设置18 m/s,转角分别设置为0°、15°、30°、45°、60°、75°、90°。
速度入口湍流度根据风洞的实测值设置为0.7%,出口设置为压力出口,出口湍流度根据实测值的平均结果设置为5% 。仿真工况的马赫数均小于0.3,可视为三维不可压缩粘性等温流场,可选取雷诺时均两方程湍流模型Realizablek-ε进行数值计算[11],通过各种湍流模型的仿真比较,确认 Realizablek-ε湍流模型的计算结果与试验结果最为接近。
2.3 稳态计算结果分析
如图8为工况1中四个刮水器的升力受风速影响的仿真结果与试验值的对比图。从图中可以发现,仿真结果的变化趋势接近二次曲线,规律性更强,且与试验结果的整体变化规律一致,峰值出现的位置也非常吻合,这一结果说明通过风洞试验方法与该数值仿真方法得到的结果具有很高的可信度和参考价值。
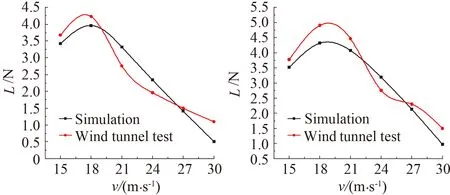
(a) 无骨刮水器 (b) A型三段刮水器
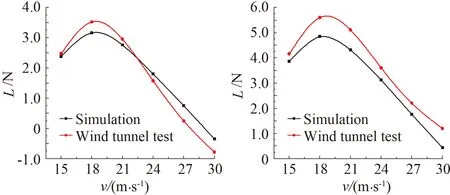
(b) B型三段刮水器 (d) 有骨刮水器
图9(a-b)所示为B型三段刮水器在转角为45°、风速为21 m/s时,上下表面静压分布图,从图中可知刮水器气动升力的产生原因正是上下表面的压力差所致,积分获得上下表面的压力值分别为2.124 N和4.883 N,两者之差即为其气动升力值。

(a) 上表面静压分布 (b)下表面静压分布
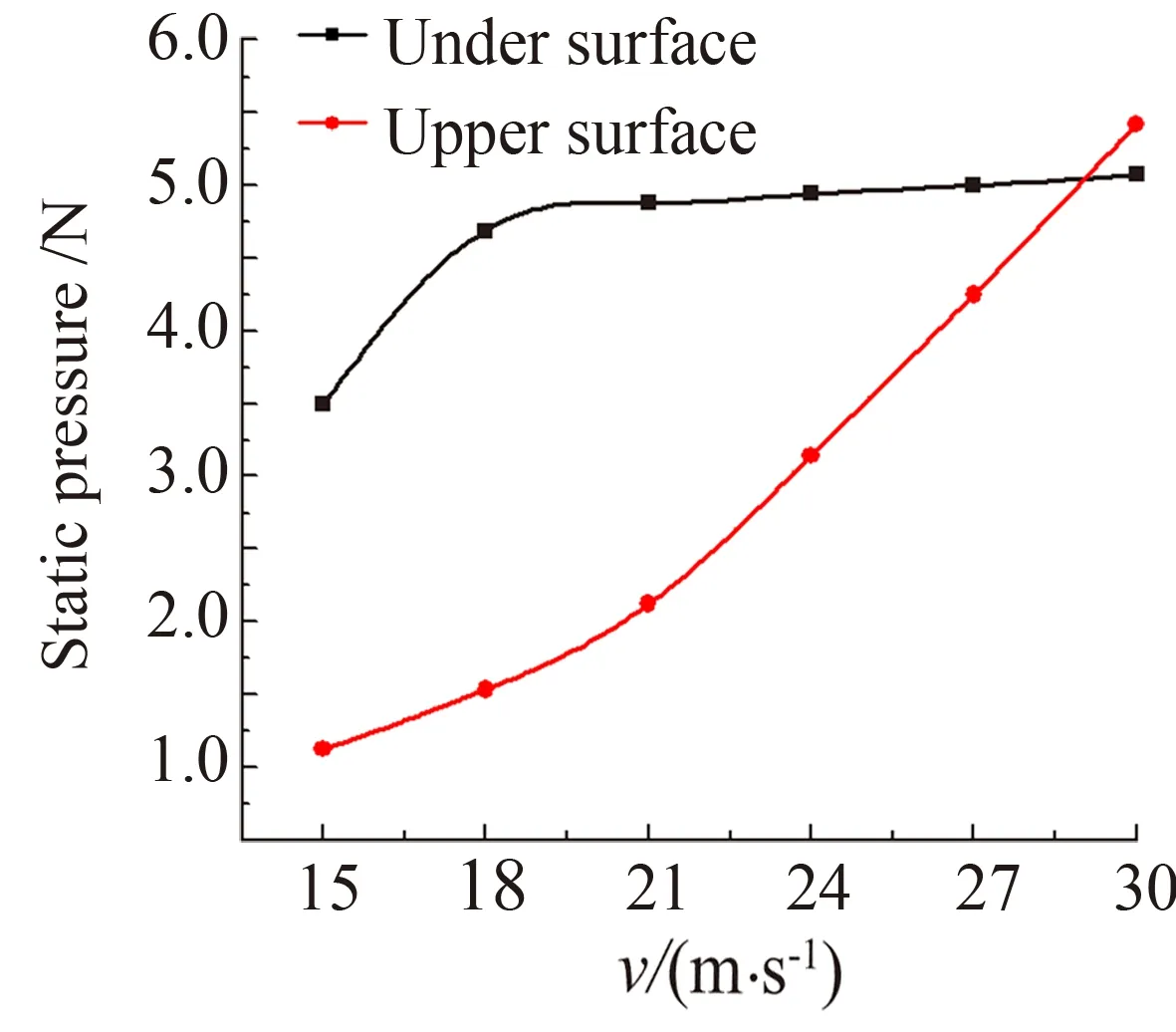
(c) 上下表面静压变化
对B型三段刮水器在45°位置时其他风速的上下表面压力进行积分处理,得到如图9(c)所示的变化趋势。从图中可以看出,上表面虽然在27 m/s之前一直比下表面的压力小,但是上表面压力随风速增大呈迅速增长的趋势,下表面压力则是在18 m/s之后缓慢增长。究其原因是由于挡风玻璃有大倾角,使刮水器的对称面与来流方向呈一定的角度,从而刮水器的迎风面为上表面,气流始终直接作用于上表面,对风速的变化非常敏感,上表面压力能随风速的增大而迅速增长,下表面为背风面,气流不会直接作用在下表面,而是作用于与之相邻的玻璃表面,在两者之间的狭小凹槽内形成旋流,此处气流速度较低,所以下表面压力变化受来流速度影响相对较小。
图10所示为工况2中4个刮水器的升力受转角影响的仿真结果和试验值的对比图。各刮水器的升力峰值均出现在45°附近,仿真结果的变化接近于正弦曲线,峰值两侧升力值逐渐减小。
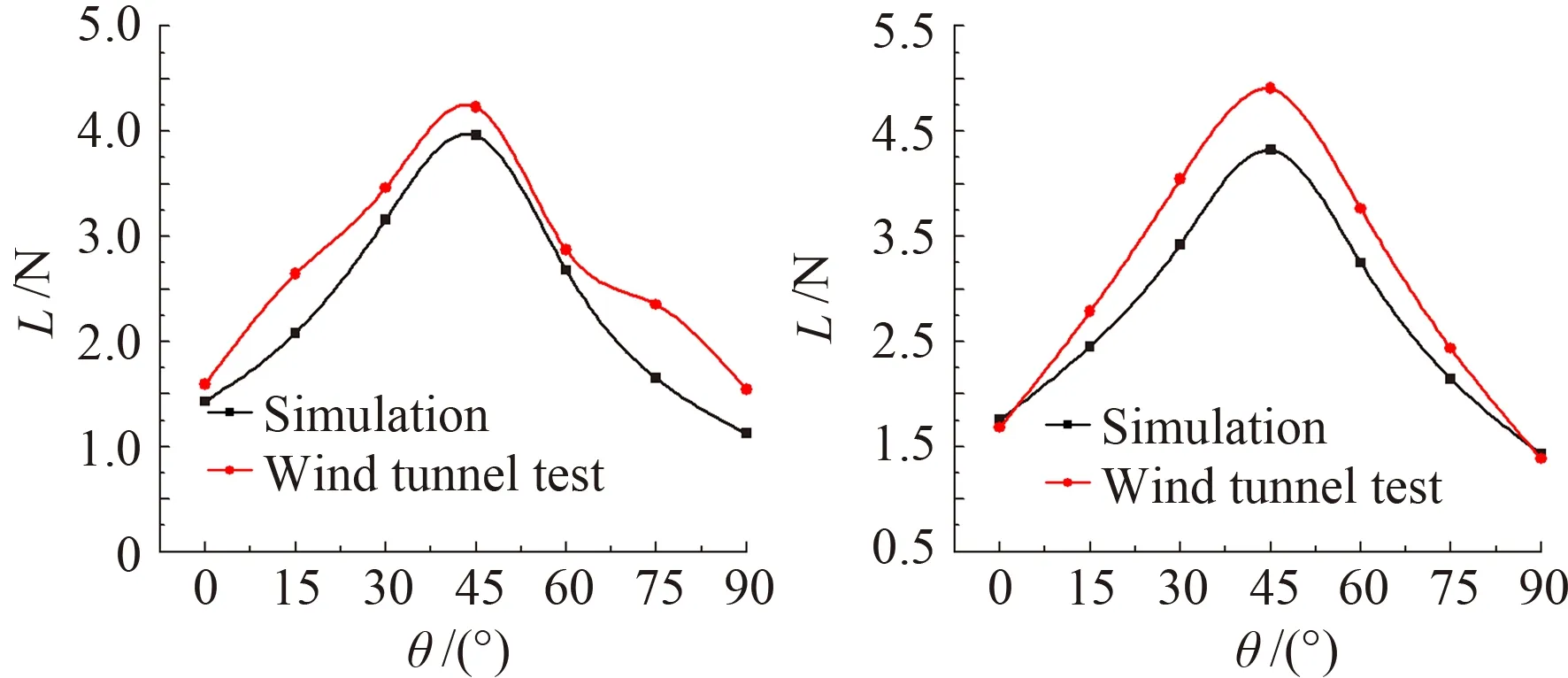
(a) 无骨刮水器 (b) A型三段刮水器
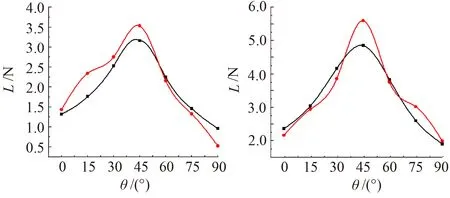
(c) B型三段刮水器 (d) 有骨刮水器
为了弄清转角的变化如何影响到刮水器周围流场,以致使升力发生变化,我们以B型三段刮水器为例进行探讨,图11为B型三段刮水器在15°、30°、45°、60°时的流线图。在15°时,刮水器处于挡风玻璃与引擎盖之间的低速区,受气流的影响很小,迎风面的平均风速约为7.5 m/s,在靠近转轴一端的背风面形成了一个螺旋涡,卷入刮水器背风面底部,涡长为1/4倍刮水器长,这时螺旋涡对刮水器背风面的作用很有限;随着转角分别增加到30°、45°时后,刮水器脱离低速区,迎风面平均风速随之增大到大约12.5 m/s、17.5 m/s,背风面螺旋涡的长度变成3/5倍、1倍刮水器长,涡旋强度也有所增加,使得卷入底部的气流对下表面的作用力增大。转角继续增大到60°后,迎风面气流速度,螺旋涡的涡长和涡旋强度相对于45°时没有明显增加,但此时刮水器展向与气流方向之间的角度变小,刮水器的迎风面积大幅减小, 且上下表面的气流较多沿着刮水器展向导出。由此可知转角较大时,较小的迎风面积与气流能顺畅通过是导致气动升力减小的主要原因。

(a) 15° (b) 30°
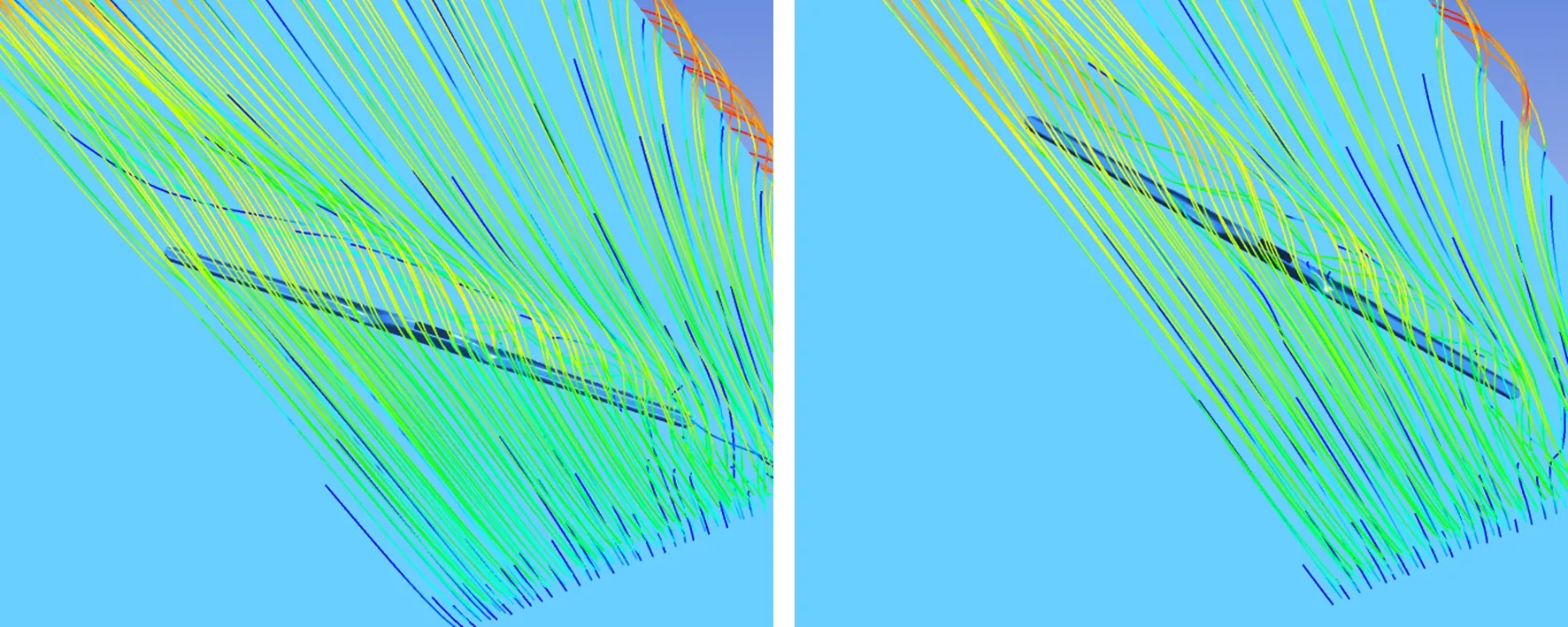
(c) 45° (d) 60°
其他三个刮水器气动升力产生机理与变化规律与B型三段刮水器相似,这里不再赘述。
3 动态转角的瞬态气动升力分析
3.1 新型动网格策略与可行性分析
对于四面体及三棱柱网格,动网格的更新方法为网格变形和局部网格重构,前者的基本思想是将网格的边理想化为节点间相互连接的弹簧,当网格变化时,根据胡克定律可以确定使节点上的合力为零的新节点位置。当运动边界的位移远远大于网格尺寸时,局部网格发生重构,生成新的网格代替旧网格,使畸变率和尺寸始终满足要求。为避免由于网格运动产生的额外误差,必须遵守动网格守恒方程,任意一个边界移动的控制体V中,广义标量φ的积分守恒方程为:
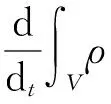
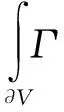
式中,ρ为流体密度,u为流体的速度矢量,ug为移动网格的网格速度,Γ为扩散系数,Sφ为φ的源项,∂V为控制体V的边界。
动网格技术在二维流场和运动边界较简单的三维流场模拟中应用广泛,如机翼和鱼尾动态模拟[12-15],对于复杂模型的边界运动模拟比较困难。本文研究的刮水器外形较为复杂,具有很多小面,且运动幅度很大,刮刷角度为90°,采用一般的动网格策略有2个缺点:
1) 刮水器表面的网格伸缩和重构时质量也会大幅下降,计算结果会出现较大的波动;
2) 刮水器表面网格小,为避免出现负体积,必须将时间步长设置很小,导致计算时间很长。此外过多的网格变化对计算机性能要求很高。
针对上述提到的问题,本文提出一种动网格域盒方法,即建立一个完全包裹刮水器的动网格域盒(下文简称域盒),在域盒内外建立两个网格区域,将域盒壁设置为Interior,计算时使刮水器、域盒以及盒内网格一起运动。此方法有以下3个优点:
1) 刮水器表面网格不再发生变化,保证了网格质量,避免了由于网格畸形导致的计算结果波动;
2) 网格的变形及重构由刮水器表面转移到域盒表面,域盒表面的网格更规整,尺寸更大,因此网格变形与重构更容易,生成的新网格质量更高;
3) 涉及变形与重构的网格量少,减轻了计算负荷。时间步长可设置较大,可提高计算效率。
为了验证此方法的可行性,本文设计了验证算例:用四棱柱代替复杂的刮水器在斜面上转动90°,采用四棱柱是为保证在无域盒动态计算时也能大角度转动,设置了无域盒、平顶域盒、圆顶域盒和仅有盒底四个对比算例,如图12(a)~图12(d)。

(a) 无域盒 (b) 平顶域盒
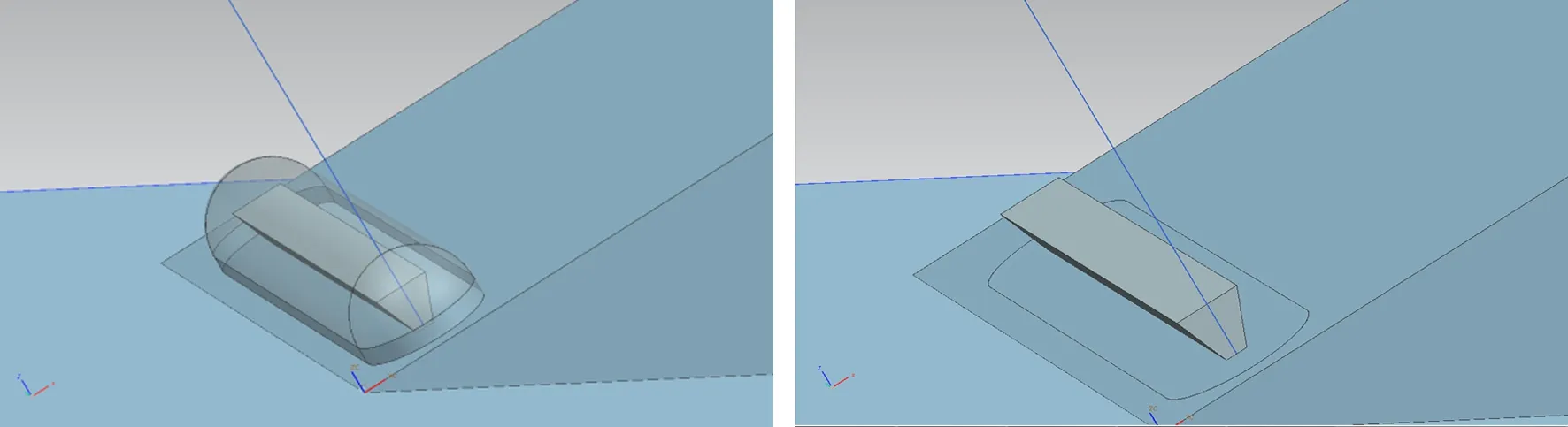
(c) 圆顶域盒 (d) 仅有盒底
表1为各算例计算完成后的网格信息和计算时间,明显可发现域盒方法能维持网格质量,并有效的提高计算效率。
如图13为0.1 s~0.6 s棱柱升力系数的瞬态计算结果,从图中可看出四个算例的变化趋势一致,且数值基本一致。另外从无域盒的计算结果可发现,在0.2 s和0.32 s时刻升力系数出现了明显跳动,这是棱柱表面的网格在前后两个时刻发生了剧烈的变化所致。而仅有盒底与有域盒的计算结果几乎一致,这一结果可证实添加域盒不会对计算结果的准确性产生影响。
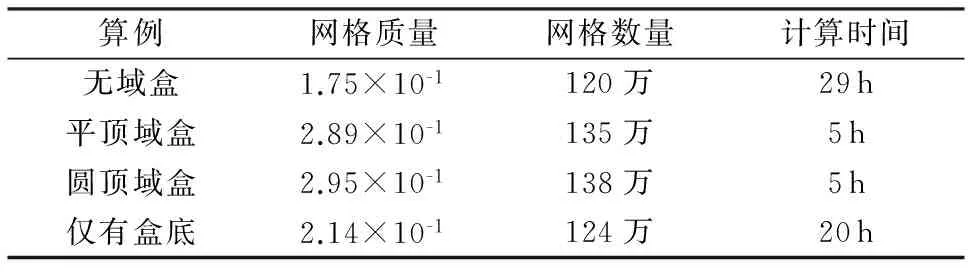
表1 验证算例的网格信息与计算时间Table 1 Mesh information and calculate time of validation example
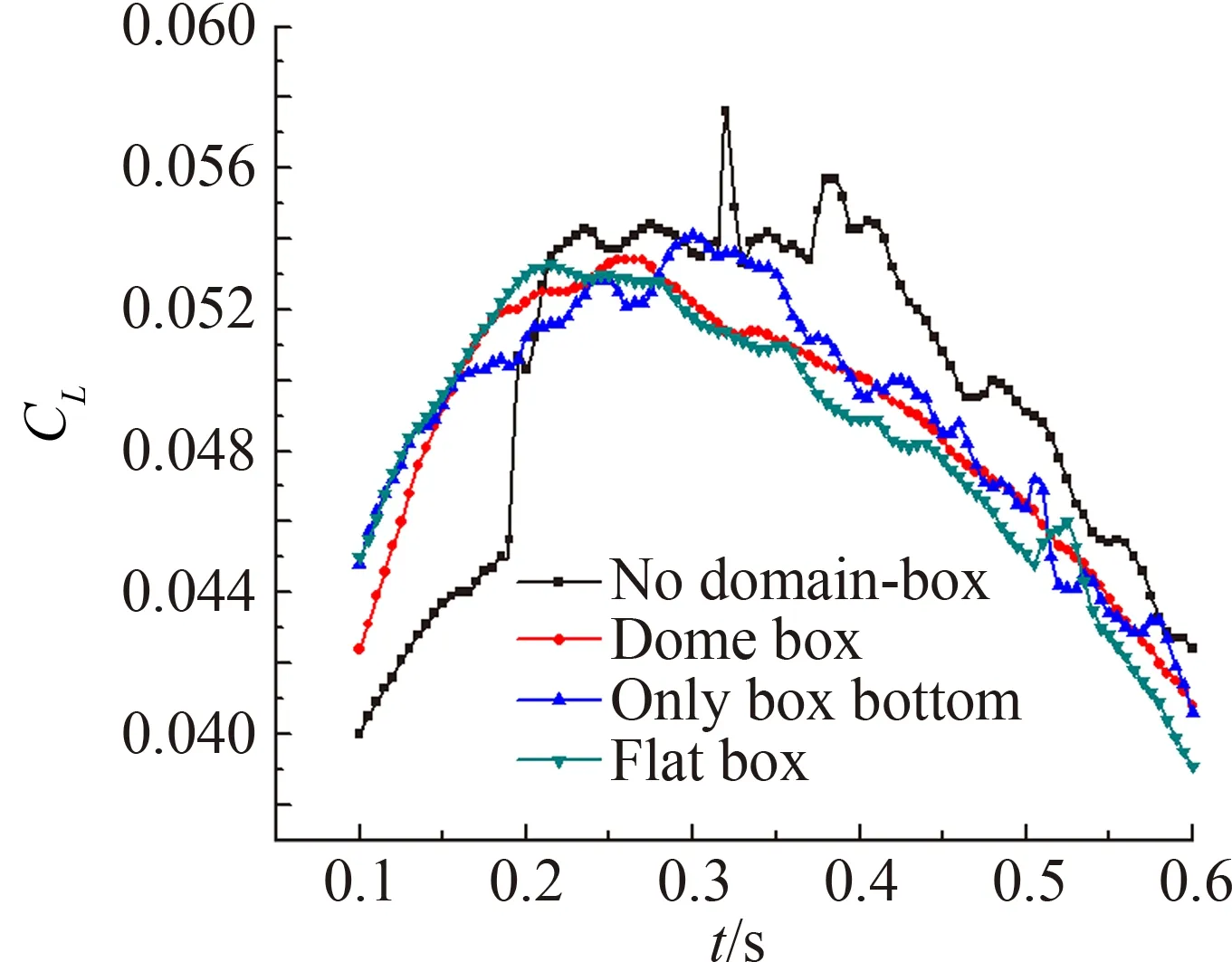
图13 升力系数验证结果Fig.13 Verification result of lift coefficient

(a) 无域盒 (b) 平顶域盒
如图14为无域盒与有平顶域盒时,棱柱转动到90°后的网格变化对比图,可以确认在有域盒时,即使棱柱在大角度转动的情况下,表面网格仍可维持很高的质量。由验证结果可知,通过添加动网格域盒可以准确而快速的实现刮水器瞬态气动升力的计算,图15为添加平顶域盒后的刮水器模型。
3.2 基于UDF的动网格域盒运动边界控制
为实现刮水器动态仿真尽可能接近实际工作情况,即以一定的转动速度上行至最大角度后短暂停顿,再以相同的速度下行至初始位置,本文通过用户自定义函数(UDF)的方式来实现这一运动方式。

图15 添加平顶域盒的刮水器模型Fig.15 Wiper model with the flat domain-box
定义挡风玻璃为可变形体,定义刮水器、域盒以及盒内网格为刚体运动,速度为1.5 rad/s,取初始位置为0°,刮水器上行至90°,停滞0.3 s后下行至初始位置,停滞0.5 s,至此一个周期结束进入下一个周期。其控制函数如下:
for (i=0;i<=n;i++)
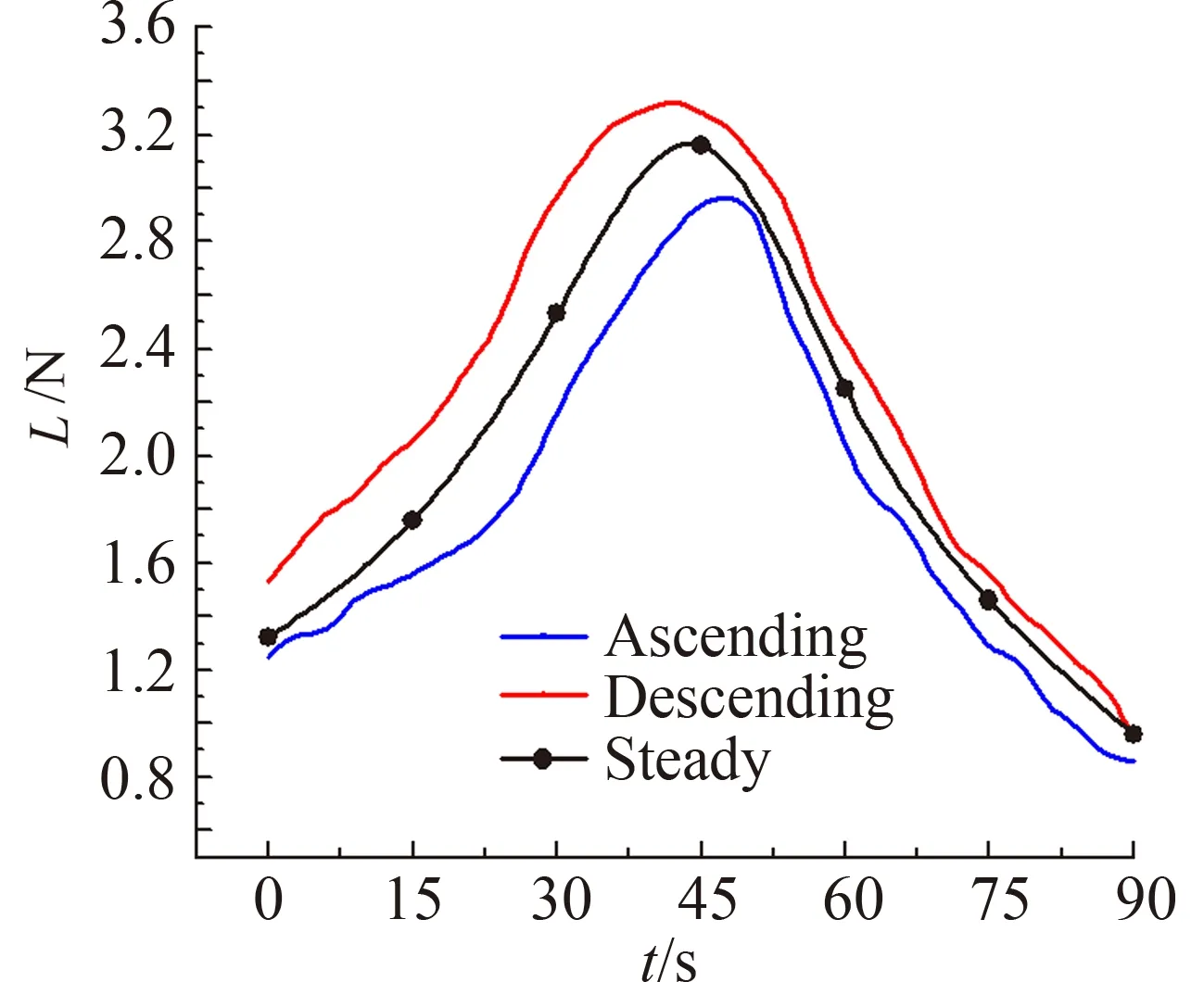
{if (2i omega[0]=1.5; 刮水器上行 else if (2i+1.35 omega[0]=-1.5; 刮水器下行 else omega[0] =0 刮水器停滞} 3.3 瞬态计算结果分析 表2为上行计算至15°时(无域盒算例因出现负体积而无法计算完成),刮水器未添加域盒与添加平顶域盒的网格信息和计算时间。相比于简单的四棱柱模型而言,运动边界更复杂的刮水器采用域盒方法优点更加凸显。 表2 动态刮水器的网格信息与计算时间(15°)Table 2 Mesh information andcalculate time of dynamic wiper(15°) 图16为刮水器刮至15°时的网格变化情况,对比图14可以看出,运动边界越复杂,域盒对于维持网格质量和尺寸的效果越明显。 (a) 无域盒 (b) 平顶域盒 图17所示为B型三段刮水器在风速为18 m/s下的瞬态计算结果与稳态结果的对比图,在转角处于0到45°时,上行时的升力小于稳态结果,下行时大于稳态结果,转角大于45°后,瞬态结果与稳态结果相差不大。此外瞬态结果峰值的出现位置分别位于稳态结果峰值处的两侧。 图17 上下行时瞬态气动升力变化与稳态结果Fig.17 Lift of dynamic wiper 为进一步了解上行与下行时刮水器周围的流场信息,截取45°时经过刮水器中心的纵截面。如图18(a),在刮水器上行时,其速度方向与气流方向一致,两者的相互作用相对较弱,刮水器周围气流能较为顺利的通过,迎风面的气流速度分布均匀,上部气流速度大约为12.5 m/s,从上至下有略微的降低,刮水器顶部负压为-140 Pa,后部气流有轻微的扰动,但未形成涡;而在刮水器下行时,如图18(b),其速度方向与气流方向相反,两者相互作用增强,虽然迎风面上部气流速度也为12.5 m/s,但从上至下的降低幅度较大,迎风面底部的速度降到了7.5 m/s,使刮水器下表面的静压增大,这是其升力增大的原因之一,此时顶部的气流扰动剧烈,有大角度的转向,使气流向上的速度分量偏大,导致顶部的负压区压力减小到-280 Pa,使刮水器受到更大的向上的拉力,这是其升力增大的原因之二,气流扰动致使刮水器后部形成了尺度较大的螺旋涡,在背风面气流以较高的速度窜进刮水器与挡风玻璃形成的凹槽内,此为刮水器升力增大的原因之三。由于上述三个原因,导致下行时的升力相对上行时有所增大。 (a) 上行 (b) 下行 本文通过对四种刮水器进行试验及仿真研究,发现气流对刮水器的影响足以降低其工作效率,在设计过程中此影响不容忽视,并得出以下结论: 1) 通过试验结果得到的气动升力最大可抵消68.6%的预压力。不同外型的刮水器气动升力特性不同,但随着刮刷角度及来流速度变化的规律一致,峰值均出现在44°、19 m/s处附近。 2) 刮水器气动升力产生的原因是上下表面的压力差,受来流影响较大。当刮水器处于不同角度时,升力的大小决定于迎风面风速,背风面螺旋涡以及气流流向与刮水器的夹角。 3) 刮水器运动时对周围的气流会造成巨大影响,瞬态模拟能更真实地反映刮水器刮刷过程中的气动特性,刮水器上行时受到的气动升力小于稳态值,下行时受到的气动升力大于稳态值。 本文采用的数值方法较好地分析了刮水器气动升力的变化规律,可以广泛应用到刮水器结构设计与稳定性分析中。 [1]Gu Zhengqi. Automobile aerodynamics[M]. Beijing: China Communications Press, 2005: 120-125. (in Chinese)谷正气. 汽车空气动力学[M]. 北京: 人民交通出版社, 2005: 120-125. [2]Shibata, Sakoda. Research on the automobile wipers floating[C]//Automobile Technology Academic Lectures, 1979, 791: 124-156. [3]Toshikazu S, Masanori S, Kunio N. A study on aerodynamic characteristics of passenger cars[R]. SAE Paper 1983-11-07. [4]Takada K, Komoriya T, Furugori Y. Numerical simulation of wiper blade uplifting on high speed traveling[C]//The Japan Society of Mechanical Engineers, 2003, 38: 38-39. [5]Lin C F, Hung M F, Tseng C Y, et al. Numerical investigation of aerodynamic effects on windshield wiper[J]. Journal of Technology, 2005, 20(4): 325-332. [6]Zhang Junhai. Numerical simulation of the aerodynamic wiper on high-speed locomotives based on FLUENT[D]. Chengdu: Southwest Jiaotong University School of Mechanical Engineering, 2010. (in Chinese)张军海. 基于FLUENT的高速机车气动刮雨器数值模拟研究[D]. [硕士学位论文]. 成都: 西南交通大学, 2010. [7]Yang Z G, Ju X M, Li Q L. Numerical analysis on aerodynamic forces on wiper system[C]//Proceedings of the Sixth International Conference on Fluid Mechanics, 2011, 1376: 213-217. [8]Ji-soo H, Tae-kwon K, Kwan-hee K, et al. A study on the lift characteristics according to the change of blade angle in car wiper[J]. Journal of Korean Society of Mechanical Technology, 2013, 15(1): 27-31. [9]Philippe Billot, Sébastien Jallet, Frédéric Marmonier. Simulation of aerodynamic uplift consequences on pressure repartition-application on an innovative wiper blade design[R]. SAE 2001 World Congress, 2001-01-1043. [10]QC/T 44-2009. 汽车风窗玻璃电动刮水器[S]. [11]He Yibin, Gu Zhengqi, Li Weiping, et al. Comparison investigation of typical turbulence models for numerical simulation of automobile external flow field[J]. Journal of System Simulation, 2012, 24(2): 467-472 [12]Liu Fangfang, Yang Canjun, Su Qi, et al. Simulation analysis and experimental research on the movements of biomimetic fin[J]. Journal of Mechanical Engineering, 2010, 46(19): 24-29. (in Chinese)刘芳芳, 杨灿军, 苏琦, 等. 仿生鱼鳍运动仿真分析及试验研究[J]. 机械工程学报, 2010, 46(19): 24-29 [13]Liu Xueqiang, Li Qing, Chai Jianzhong, et al. A new dynamic grid algrithm and its application[J]. Acta Aeronautica et Astronautica Sinica, 2008, (04): 817-822. (in Chinese)刘学强, 李青, 柴建忠, 等. 一种新的动网格方法及其应用[J]. 航空学报, 2008, (04): 817-822 [14]Chen Lili, Song Bifeng, Song Wenping, et al. Dynamic fluid-structure coupling research for micro flapping wing[J]. Acta Aerodynamica Sinica, 2013, 31(2): 175-180. (in Chinese)陈利丽, 宋笔锋, 宋文萍, 等. 基于结构动力学的平板扑翼气动弹性方法研究[J]. 空气动力学学报, 2013, 31(2): 175-180. [15]Zhu Bing, Zhu Xiaoping, Zhou Zhou, et al. Simulation of unsteady multi-body flowfield involving relative movement based on unstructured mesh[J]. Acta Aerodynamica Sinica, 2013, 31(2): 181-185. (in Chinese)朱冰, 祝小平, 周洲, 等. 基于非结构动网格的多体分离数值仿真研究[J]. 空气动力学学报, 2013, 31(2): 181-185. The experimental and numerical research on aerodynamic lift of automobile windshield wiper Tan Peng1, Gu Zhengqi1,2,*, Chen Zhen1, Feng Chengjie1, Zhang Qidong1 (1.StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBodyHunanUniversity,Changsha410082,China;2.HunanUniversityofTechnology,Zhuzhou412007,China) Current researches on the aerodynamic lift of automobile windshield wiper are widely focused on the steady numerical calculation of static angle, and the research results of different papers are various, yet no test result can be found to support the simulations. A wind tunnel test is designed and executed to validate and verify the simulation method. Steady aerodynamic lifts of four kinds of wipers with different wind speeds and different rotate angles are measured using multi-point test method. The combination of wind tunnel test and steady numerical calculation helps understanding of lift generation and variation. Furthermore, a new dynamic mesh strategy called the domain-box of dynamic mesh is proposed, the transient aerodynamic lift is simulated and analyzed with User Definition Function method (UDF). The researching result shows that the maximum aerodynamic lift of all four wipers can counteract 68.6% of the precompression, the effect of aerodynamic lift on the stability of wiper cannot be ignored. The lift will achieve its maximum at a certain wind speed and angle, and the magnitude of lift depends on the wind speed of the windward side, the spiral vortex of the leeward and the angle between wind and wiper. Furthermore, the aerodynamic lift is lower than that of steady case when the wipers ascends, and higher when descends. windshield wiper; aerodynamic lift; wind tunnel test; domain-box of dynamic mesh 0258-1825(2017)02-0234-08 2015-01-27; 2015-05-27 中央财政支持地方高校专项资金项目-创新团队(0420036017);交通运输部新世纪十百千人才培养项目(20120222);湖南大学汽车车身先进设计与制造国家重点实验室自主课题资助项目(734215002) 谭鹏(1988-),男,湖北利川人,硕士研究生,从事汽车空气动力学研究. E-mail:jordanvon@163.com 谷正气*(1963-),男,湖南长沙人. E-mail: guzhengqi63@126.com 谭鹏, 谷正气, 陈阵, 等. 汽车刮水器气动升力的风洞试验及数值研究[J]. 空气动力学学报, 2017, 35(2): 234-241. 10.7638/kqdlxxb-2015.0011 Tan P, Gu Z Q, Chen Z, et al. The experimental and numerical research on aerodynamic lift of automobile windshield wiper[J]. Acta Aerodynamica Sinica, 2017, 35(2): 234-241. U461.1 A doi: 10.7638/kqdlxxb-2015.0011


4 结 论
