随机投影下的Plane-Gaussian人工神经网络*

2017-04-27杨绪兵张福全

数据采集与处理 2017年2期

关键词：隐层投影平面

冯哲杨绪兵张福全

(南京林业大学信息科学技术学院，南京,210037)

随机投影下的Plane-Gaussian人工神经网络*

冯哲杨绪兵张福全

(南京林业大学信息科学技术学院，南京,210037)

针对平面高斯神经(Plane-Gaussian, PG)网络采用k-平面聚类算法得到网络参数，使得网络训练时间过长，且易陷入局部极小值的问题，借鉴极限学习机(Extreme learning machine, ELM)中网络参数随机选择的方式，提出了随机投影下的平面高斯神经网络(Plane-Gaussian network based on random projection, RandPG)。该网络采用随机投影的方式确定隐层激活函数的参数，然后利用Moore-Penrose广义逆求解输出层权值。理论上证明该网络具有全局逼近性。同时，对呈直线型和平面型的人工数据集以及UCI标准数据库中的分类数据集进行测试，结果表明，RandPG网络提供了一种简便的参数学习方法，并且在继承了PG网络对呈子空间分布的数据分类具有优势的情况下，显著提高了网络的学习速度。

人工神经网络；随机投影；平面；高斯；极限学习机

引言

近十几年来，针对神经网络的学术研究非常活跃，研究者们提出了上百种的神经网络模型，其中应用最广泛的神经网络模型有反向传播(Back propagation, BP)网络和径向基函数(Radial basis function, RBF)网络。但是BP网络存在计算量大、学习速度慢和易陷入局部极小值等问题；而RBF网络的精度和稳定性由隐含层核函数的中心与宽度决定，导致网络的结构难以确定且适应性较差。

针对以上问题，黄广斌等[1]在单隐层前馈神经网络的基础上提出了一种高效的学习算法——极限学习机(Extreme learning machine, ELM)。与传统的神经网络不同，ELM网络的输入权重和隐层偏置随机生成，无需进行反复调整，其输出权值用最小二乘估计法就能得到唯一的最优解。ELM具有较快的学习速度和良好的泛化性能，且网络结构简单。越来越多的学者对其在特征学习、聚类、回归和分类问题上进行研究，现今ELM已经在模式识别[2-3]、自动控制[4-5]、预测[6-7]和建模[8-9]等领域得到了广泛的应用。但是ELM并不具备明确的几何意义。杨绪兵等[10]从平面拟合的角度，采用“平面原型”[11]代替RBF网络的“点原型”，设计出适合平面型分布数据的平面高斯(Plane-Gaussian, PG)神经网络模型。由于PG网络在训练过程中采用k-平面聚类算法(k-plane dustering, kPC)完成样本的类别划分，这就不可避免地会造成网络训练时间过长，且易陷入局部极小值等问题。

为了克服这些缺点，本文借鉴ELM随机产生参数的思想，结合随机投影理论，对PG网络进行改进，提出了随机投影下的平面高斯神经网络(Plane-Gaussian network based on random projection, RandPG)。RandPG网络中的分类方向随机选择，避免聚类，突破了陷入局部最优解的限制，网络训练时间大大降低。同时随机投影将高维数据映射到低维空间中，降低了运算的复杂性。RandPG网络在保持对呈子空间分布数据分类更有效的优势的同时，学习速度得到了进一步提高。

1 平面高斯网络

PG网络是以平面高斯为激活函数，即用超平面代替高斯函数中的数据中心点，通过最小化样本点到最近超平面距离之和来获得k个原型超平面，PG函数定义为

(1)

图1 平面高斯函数的三维可视化 Fig.1 3D visualization of PG function

(2)

式中wi和bi分别表示超平面pi的单位法向量和截距。

kPC算法的执行过程包含反复将样本点分配给距其最近的超平面所对应的聚类和计算新的超平面的法向量和截距两步，直至样本归类不再变化为止。

kPC算法能对未知样本集进行有效聚类，但是通过迭代方法求解，会导致网络训练速度过慢，且很容易产生局部极小值。

2 随机投影原理

随机投影(Randomprojection，RP)技术[13]是指将高维空间中的点投影到一个随机选取的低维子空间内，它可将原来的高维问题转化到低维空间来求解。下面给出随机投影的定义。

原始的d维数据矩阵Xd×n，在k×d维的随机矩阵R的作用下，被投影到一个k维的子空间中，其中矩阵R的每一行都单位化。投影问题可以描述为

(3)

最近一项研究表明，人类能从极少量的数据中学习，可能是因为随机映射算法[15]，而神经网络正是根据人脑的生物结构所设计。因此，在如今大数据时代，随机映射算法必将成为机器学习领域内一项非常有用的技术。

图2 3层RandPG网络结构图 Fig.2 Three-layer Rand-PG neural network

3 RandPG网络

RandPG的网络结构如图2所示，其包含一个输入层，一个隐层和一个输出层。输入层中包含d个神经元，表示样本的d维属性。与RBF网络一样，输入层与隐层通过权值为1的权矩阵连接。隐层采用式(1)的PG函数作为激活函数，通过随机投影的方法确定参数wi，bi(i=1,2,…,c)后，隐层和输出层的连接关系可用权值矩阵U表示。因此，输入输出层间的对应关系可描述为如下映射

(4)

即

(5)

式中

(6)

3.1 RandPG网络的学习过程

RandPG网络的训练过程分为两个阶段：第一阶段采用随机投影的方法产生隐含层中激活函数的参数wi值，由平面计算公式计算出bi值；第二阶段通过Moore-Penrose广义逆计算隐层与输出层的连接权值矩阵U。具体的步骤描述如下。

(3) 采用0-1编码标记目标输出矩阵。样本类别标号用一个只有0和1组成的列向量来表示。例如某样本xi属于第l类，则其第l个分量为1，其他元素都为0，则其0-1编码表示为yi=(0,…,0,1,0,…,0)T。N个样本的目标输出矩阵表示为Y=(y1,y2,…,yN)。

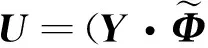
按照上述步骤求得隐层激活函数的中心超平面的法向量wi、截距bi和宽展度σi及隐层与输出层的连接权值矩阵U后，就完成了RandPG网络的构建。

图3 平面高斯函数带状激活区 Fig.3 Band-shaped field of plane-Gaussian function

3.2 RandPG网络的全局逼近性

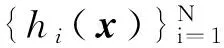
证明：隐层输出矩阵H的第i列c(bi)=[gi(x1),…,gi(xN)]T=[g(wi·x1+bi),…,g(wi·xN+bi)]T，在欧氏空间RN中bi∈(a,b)，(a,b)为R上的一段区间。可以证明向量c不属于任何维度小于N的子空间。

由于wi是在连续概率分布上随机选择，那么可以假设对于所有的k≠k′，wi·xk≠wi·xk′。假设c属于N-1维的子空间，那么就存在一个向量α正交于这个子空间，即有

(7)

式中：dk=wi·xk，k=1,…,N且对于bi∈(a,b)，z=α·c(a)。假设αN≠0，式(7)可以扩展成为

(8)

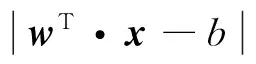
(9)

式中g(l)为激活函数g关于bi的第l阶导数。但是，只有N-1个自由系数(γ1,…,γN-1)对应于推导出的超过N-1个的线性方程，这是相背的。因此向量c不属于任何维度小于N的子空间。

所以从任意区间(a,b)上随机选择N个隐层节点的偏置b1,…,bN使得相应的向量c(b1),c(b2),…,c(bN)扩展到RN是可能的，这意味着对于任意的wi∈Rn，bi∈R，根据连续概率分布，H矩阵满秩。

4 实验结果

为验证RandPG网络的分类性能，本文分别在呈直线型分布和呈平面型分布的人工数据集和8个UCI数据集上进行实验，并与PG网络和ELM在分类精度和分类时间上进行比较。实验均是从整个样本数据集中随机抽取一半作为训练样本，剩下的一半作为测试样本。每个数据集分别进行50次分类实验。对于实验结果的评价标准，由于RandPG网络和PG网络的投影方向具有几何意义，代表的是拟合平面，所以选取50次分类实验中训练精度和测试精度的最大值作为最优投影方向，而ELM算法没有明确的几何意义，所以选取50次分类实验中训练精度和测试精度的平均值作为最终结果，训练时间和测试时间都取50次实验的平均值。为了保证3种算法的公平性，PG网络和ELM的隐层节点数都与类别个数相同。

4.1 人工数据集

人工数据集的实验主要是为了检验RandPG网络对呈子空间分布的数据的分类是否具有优越性。对此，实验设计了二维空间中的多类直线型分布数据和多维空间中的平面型分布数据。

4.1.1 直线型数据集

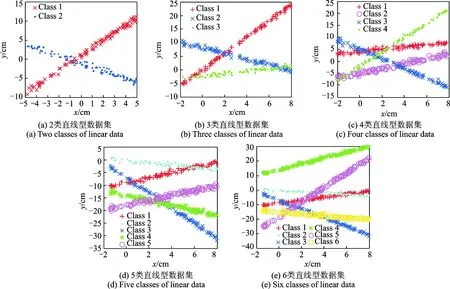
图4 2～6类直线型数据分布图Fig.4 Different classes of linear data distribution diagram

分别用RandPG，PG和ELM3种方法训练上述5个二维空间中呈直线分布的人工数据集，比较3种神经网络随着类别数的增加对直线型数据的分类性能，训练精度和测试精度分别如图5和图6所示，训练时间和测试时间分别如图7和图8所示。

从图5～8可以看出，当类别数较少时，PG网络的分类精度较高，随着类别数的增加，RandPG网络在分类精度方面展现出了优势，而ELM对直线型分布的数据分类精度都不高。每种方法的训练精度和测试精度的趋势走向基本一致，因此通过训练过程得到的参数对网络的泛化能力起着至关重要的作用。从训练时间的角度看，RandPG网络和ELM的训练速度都很快，而PG网络的训练时间大概是它们的10倍；这和每种网络参数产生的原理相吻合，PG网络产生参数时需要逐步迭代，势必会耗费更多的时间，而其他两种网络都是随机产生参数，所以在训练时间上比较有优势。

4.1.2 平面型数据集

分别在三维、四维和五维空间设计呈平面状分布的数据，每个空间都是包含3类平面。三维空间中的第一类样本抽样于平面x-y-z=0,[y,z]∈(-4,5)，在x轴上附加范围在(-0.5,0.5)的随机噪声扰动；第二类平面抽样于平面2x+y+5z-2=0,[x,z]∈(-4,5)，在y轴上附加范围在(-0.5,0.5)的随机噪声扰动；第三类平面抽样于3x-2y+z-3=0,[x,y]∈(-4,5)，并在z轴上附加范围在(-0.5,0.5)的随机噪声，每类包含100个点。数据分布如图9所示。

图5 直线型分布数据的训练精度

Fig.5Trainingaccura-cyoflineardistri-butiondata

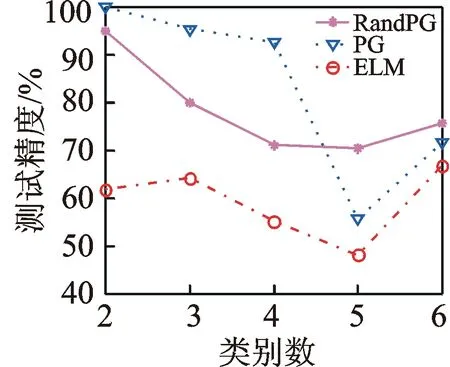
图6 直线型分布数据的测试精度

Fig.6Testingaccuracyoflineardistribu-tiondata

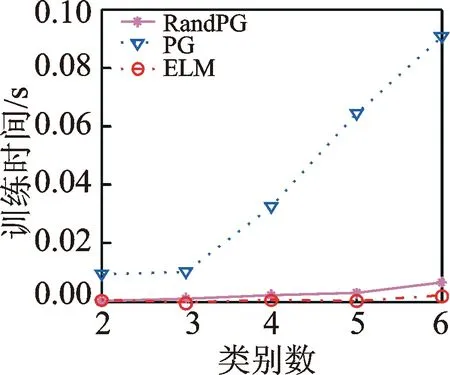
图7 直线型分布数据的训练时间

Fig.7Trainingtimeoflineardistributiondata

图8 直线型分布数据的测试时间

Fig.8Testingtimeoflineardistributiondata

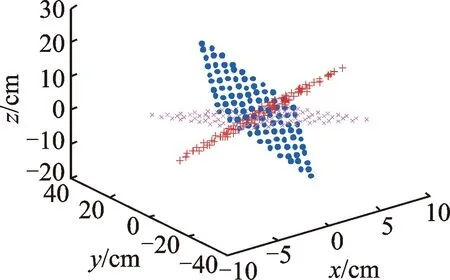
图9 三维平面型数据分布图 Fig.9 3D plane data distribution

四维空间中的第一类样本抽样于平面a+b-2c-4d-1/2=0,[b,c,d]∈(-4,5)，在a轴上附加范围在(-0.5,0.5)的随机噪声扰动；第二类平面抽样于平面a-2b+c+2/3d+3=0,[a,b,d]∈(-4,5)，在c轴上附加范围在(-0.5,0.5)的随机噪声扰动；第三类平面抽样于-2a-3b+5c+d-1=0,[a,b,c]∈(-4,5)，并在d轴上附加范围在(-0.5,0.5)的随机噪声。每类样本包含1 000个点。

五维空间中的样本点分别抽样于平面a+2b-3c+4d+2e+2=0，3a-b+5c-2d+3e+4=0和-a+3b-2c+d+4e+3=0，a，b，c，d轴的范围是均值为0，方差为1的正态随机分布，e轴的值通过平面公式计算得到。每类样本包含1 000个点。

对三维、四维和五维空间中平面型数据的实验结果如图10～12所示，其中图10和图11分别表示训练精度和测试精度，图12和图13分别描绘了训练时间和测试时间。

实验结果表明，PG网络在平面型数据集上的分类具有较大的优势，不管在哪一维空间中，分类精度都达到了90%以上。但是随着空间维数的增加，PG网络的训练时间急剧增加，是RandPG网络的百倍以上，所以对于高维数据集，RandPG网络在分类时间上具有较大的优势。与ELM相比，RandPG网络对平面型分布数据的分类精度略高，而在训练时间上，两者相差无几。

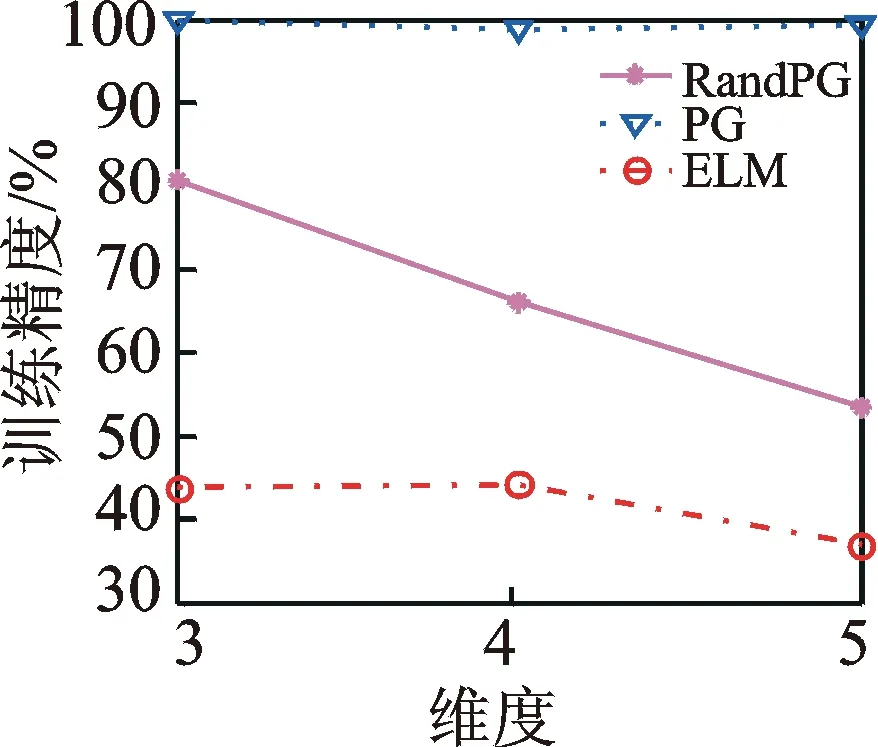
图10 平面型分布数据的训练精度

Fig10Trainingaccuracyofplanedata

图11 平面型分布数据的测试精度

Fig.11Testingaccuracyofplanedata

图12 平面型分布数据的训练时间

Fig.12Trainingtimeofplanedata

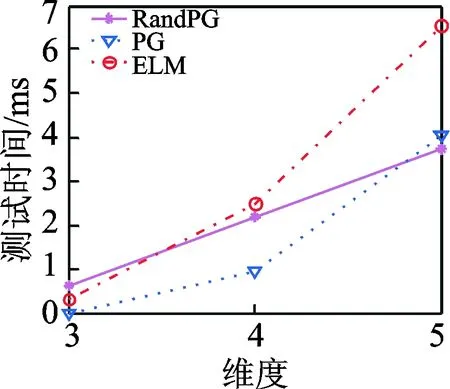
图13 平面型分布数据的测试时间

Fig.13Testingtimeofplanedata

4.2UCI数据集

为了检验RandPG网络对真实数据集的分类能力，本文选取glass，ionosphere，iris，lenses，new_thyriod，soybean_small，dermatology和ecoli8个UCI数据集(http:∥archive.ics.uci.edu/ml)进行实验，数据集的基本信息如表1所示。

表1 UCI数据集基本信息

在8个UCI数据集上的实验结果如表2所示。从表2可以很明显地看出RandPG网络对其中大部分数据集的分类精度都是最高的。PG网络在ionosphere,new_thyriod,dermatology和ecoli等数据集上的分类精度虽然与RandPG网络很接近，但是需花费数十倍甚至百倍的训练时间来完成每一次实验。这说明采用随机投影的方式，经过多次实验不仅能寻找到最优的投影方向，而且能节省算法一步步迭代所耗费的时间，RandPG网络在分类精度和分类时间上都具有较大的优势。在3种方法的隐层节点数都与样本类别数相同的条件下，ELM的分类精度明显处于劣势。这是因为ELM的网络结构决定了必须提供足够多的隐层节点个数才能保障其分类精度，而在实际情况下不可能提供无限多个隐层节点数，这样会增加网络的复杂性。在分类时间上，由于ELM算法的隐层参数也是随机产生，所以与RandPG有着相同数量级的训练时间。

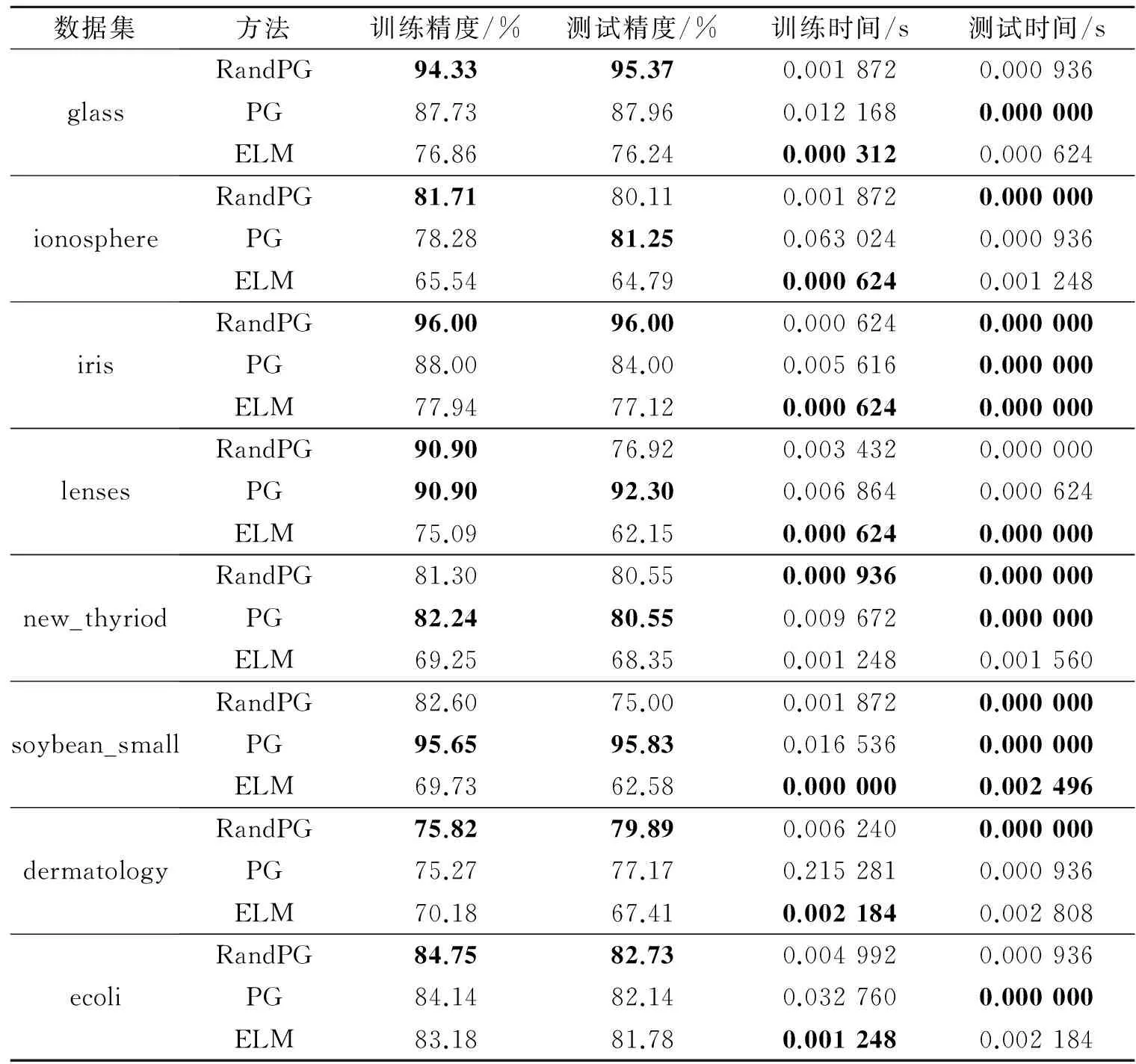
表2 UCI数据集上的实验结果

5 结束语

针对PG网络通过聚类方法确定隐层激活函数参数的缺点，本文借鉴ELM随机产生网络参数的思想，提出了RandPG网络。该网络运用随机投影的方法确定网络的结构和隐层的权值，一定程度上避免了网络训练易陷入局部极小值的问题，使得分类结果更稳定。通过对直线型、平面型数据集及UCI标准数据库中部分分类数据集的测试，结果表明，RandPG神经网络不仅继承了PG网络适用于平面型数据分类的特性，而且其学习速度明显有所提高。较之ELM，该网络具有清晰的几何意义，且隐节点个数与数据集类别数相同，无需人为干预设定。将所提出的RandPG神经网络应用于复杂的呈子空间分布的数据分类问题，可以大大提高分类的效率和准确率。在今后的研究工作中，可以考虑将RandPG网络应用于回归问题，也可以设计多隐层的RandPG网络。

[1] Huang Guangbin, Zhu Qinyu, Siew C K. Extreme learning machine: Theory and application[J]. Neurocomputing, 2006, 12(1): 489-501.

[2] 卢涛，杨威，万永静．基于图像超分辨极限学习机的极低分辨率人脸识别[J]．计算机应用，2016，36(2)：580-585.

Lu Tao, Yang Wei, Wan Yongjing. Very low resolution face recognition via super-resolution based on extreme learning machine[J]. Journal of Computer Applications, 2016, 36(2): 580-585.

[3] An Le, Yang Songfan, Bhanu B. Efficient smile detection by extreme learning machine[J]. Neurocomputing, 2015, 149: 354-363.

[4] Rong Haijun, Wei Jintao, Bai Jianming, et al. Adaptive neural control for a class of MIMO nonlinear systems with extreme learning machine[J]. Neurocomputing, 2015, 149: 405-414.

[5] Gao Xianghui, Wong K I, Wong P K, et al. Adaptive control of rapidly time-varying discrete-time system using initial-training-free online extreme learning machine[J]. Neurocomputing, 2016, 194: 117-125.

[6] 王保义，赵硕，张少敏．基于云计算和极限学习机的分布式电力负荷预测算法[J]．电网技术，2014，38(2)：526-531.

Wang Baoyi, Zhao Shuo, Zhang Shaomin. A distributed load forecasting algorithm based on cloud computing and extreme learning machine[J]. Power System Technology, 2014, 38(2): 526-531.

[7] Mulia I E, Asano T, Nagayama A. Real-time forecasting of near-field tsunami waveforms at coastal areas using a regularized extreme learning machine[J]. Coastal Engineering, 2016, 109: 1-8.

[8] 张英堂，马超，李志宁，等．基于快速留一交叉验证的核极限学习机在线建模[J]．上海交通大学学报，2014，48(5)：641-646.

Zhang Yingtang, Ma Chao, Li Zhining, et al. Online modeling of kernel extreme learning machine based on fast leave-one-out cross-validation[J]. Journal of Shanghai Jiaotong University, 2014, 48(5): 641-646.

[9] Liu Zhen, Li Hanxiong. Extreme learning machine based spatiotemporal modeling of lithium-ion battery thermal dynamics[J]. Journal of Power Sources, 2015, 277: 228-238.

[10]Yang Xubing, Chen Songcan, Chen Bin. Plane-Gaussian artificial neural network[J]. Neural Computing and Applications, 2012, 21(2): 305-317.

[11]王颖．基于超平面原型的聚类算法及相应扩展神经网络的研究[D].南京:南京航空航天大学,2006.

Wang Ying. Research on hyperplane prototype clustering algorithm and its generalization in neural networks[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006.

[12]Bradley P S, Mangasarian O L. k-Plane clustering[J]. Journal of Global Optimization, 2000, 16(1): 23-32.

[13]Fern X Z, Brodley C E. Random projection for high dimensional data clustering: A cluster ensemble approach[C]//International Conference on Machine Learning(ICML). Washington D C:[s.n],2003: 186-193.

[14]Johnson W B, Lindenstrauss J. Extensions of Lipschitz mappings into a Hilbert space[J]. Contemporary Mathematics, 1984, 26(1):189-206.

[15]Arriaga R I, Rutter D, Cakmak M, et al. Visual categorization with random projection[J]. Neural Computation, 2015, 27(10): 2132-2143.

Plane-Gaussian Artificial Neural Network Based on Random Projection

Feng Zhe, Yang Xubing, Zhang Fuquan

(College of Information Science and Technology, Nanjing Forestry University, Nanjing, 210037, China)

For the Plane-Gaussian (PG) artificial network, its network parameters are generated from k-plane clustering algorithm in training phase. Compared with random parameters of extreme learning machine (ELM), PG is a time-consumer and easy to trap into local optimal solution. To improve the performance of PG network, inspired by ELM in this paper, a new training method based on random projection for PG network, termed as RandPG, is proposed. Typically, for the three-layer network, the weight matrix between input and hidden layers is selected by random projection to speed training network, and the weight matrix between hidden and output layers is obtained by Moore-Penrose generalized inverse. It is proved that the network has global approximation theoretically. Meanwhile, the effectiveness of this network is tested on the line-distribute datasets, plane-distribute datasets and several UCI datasets. The results indicate that RandPG provides a simple and convenient way to train parameters of neural network, and it not only follows the advantage of PG network, which is more suitable for classifying subspace-distribute datasets, but also significantly accelerates its learning speed.

artificial neural network; random projection; plane; Gaussian; extreme learning machine

国家自然基金(61375057，31670554)资助项目；江苏省自然科学基金(BK20161527)资助项目；江苏高校品牌专业建设工程资助项目。

2016-09-12；

2016-10-28

TP391