多角度处理一道静摩擦力问题

涂德新

(江西师范大学附属中学，江西 南昌 330046)

多角度处理一道静摩擦力问题

涂德新

(江西师范大学附属中学，江西 南昌 330046)

本文对一道有关静摩擦力的问题进行多角度处理,首先给出典型的错误的解法,通过数学方法分析后指出错误的原因,然后给出多种简洁直观的方法进行求解,并将该问题进行拓展,以期达到融会贯通的目的．

静摩檫力;倾角;法向量;投影面积;分解;等效重力

题目.如图1所示,在水平桌面上放置一个正方形薄木板abcd,在木板的正中间放一个质量为m的木块．先以木板的ad边为轴缓慢将木板转θ角,再以ab边为轴将木板向上缓慢转θ角．整个过程中木块没有滑动,则转动后木块受到的摩擦力大小为

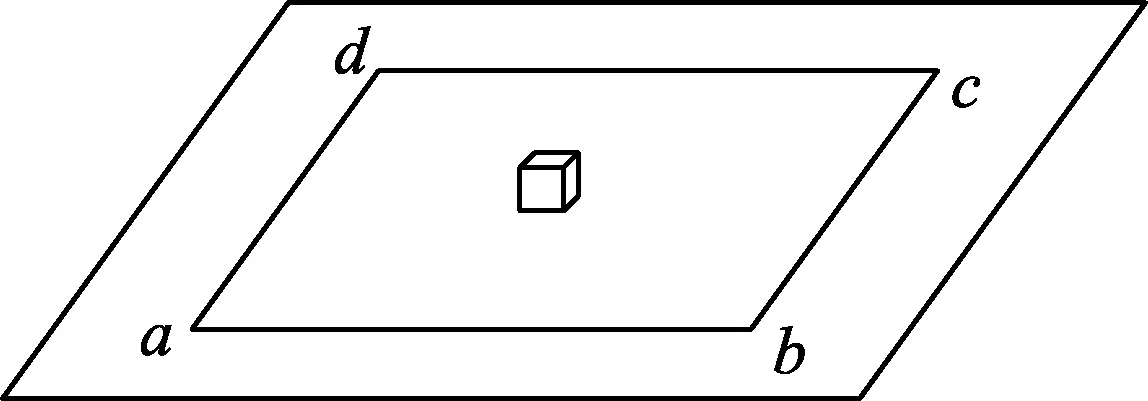
图1

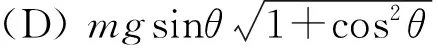
错误解法:关键是求出木板转动后与水平桌面间的二面角，如图2所示.

图2

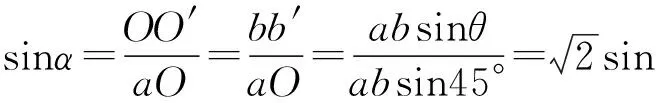
于是木块受到的摩擦力大小为

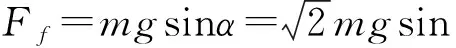
错误原因:误认为两次转动后,b点与d点等高．

下面给出几何分析过程.首先分析一下坐标系旋转后的坐标与原坐标之间的变换关系．

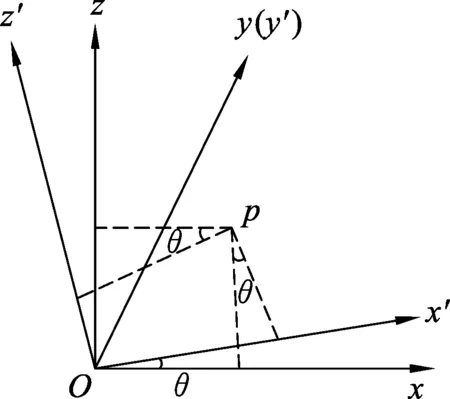
图3

如图3所示,坐标系O-xyz绕y轴沿逆时针转θ角变为O′-x′y′z′,某点P在坐标系O-xyz中的坐标为(x,y,z),在坐标系O′-x′y′z′中的坐标为(x′,y′,z′),由几何关系可知坐标变换公式为

x=x′cosθ-z′sinθ，

y=y′，

z=x′sinθ+z′cosθ.

设正方形abcd的边长为l,如图4所示,平面1绕轴ad向上转θ角变为平面2,平面2绕ab边向上转θ角变成平面3,平面2所在的坐标系为O′-x′y′z′,分析有平面3中的正方形abcd在坐标系O′-x′y′z′中的坐标为

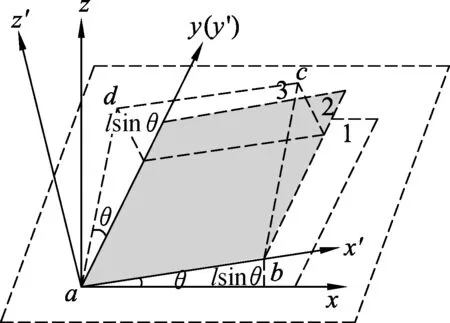
图4

a(0,0,0),b(l,0,0)，

c(l,lcosθ,lsinθ),d(0,lcosθ,lsinθ).

再转换成在坐标系O-xyz中的坐标为

a(0,0,0),b(lcosθ,0,lsinθ)，

c(lcosθ-lsin2θ,lcosθ,lsinθ+lsinθcosθ),

d(-lsin2θ,lcosθ,lsinθcosθ).

可以发现旋转两次之后zb=lsinθ以及zd=lsinθcosθ,b点与d点显然不等高．

解法1:向量分析法.用数学方法求出旋转两次后平面3的倾角,再求此时滑块受到的静摩擦力．

按照上述分析有ab=(lcosθ,0,lsinθ),ad=(-lsin2θ,lcosθ,lsinθcosθ).

展开后有

ab×ad=l2(-sinθcosθi-sinθj+cos2θk).

此向量刚好沿平面3的法线方向,设此平面与竖直方向的夹角为φ,则

化简为 cosφ=cos2θ.

分析后可以发现平面3与水平面的夹角也为φ,故滑块所受的静摩檫力为

代入可得

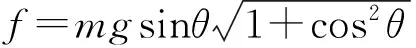
解法2:法向量旋转法.可以通过研究旋转两次后木板所在平面的法向量来分析滑块所受的摩擦力．

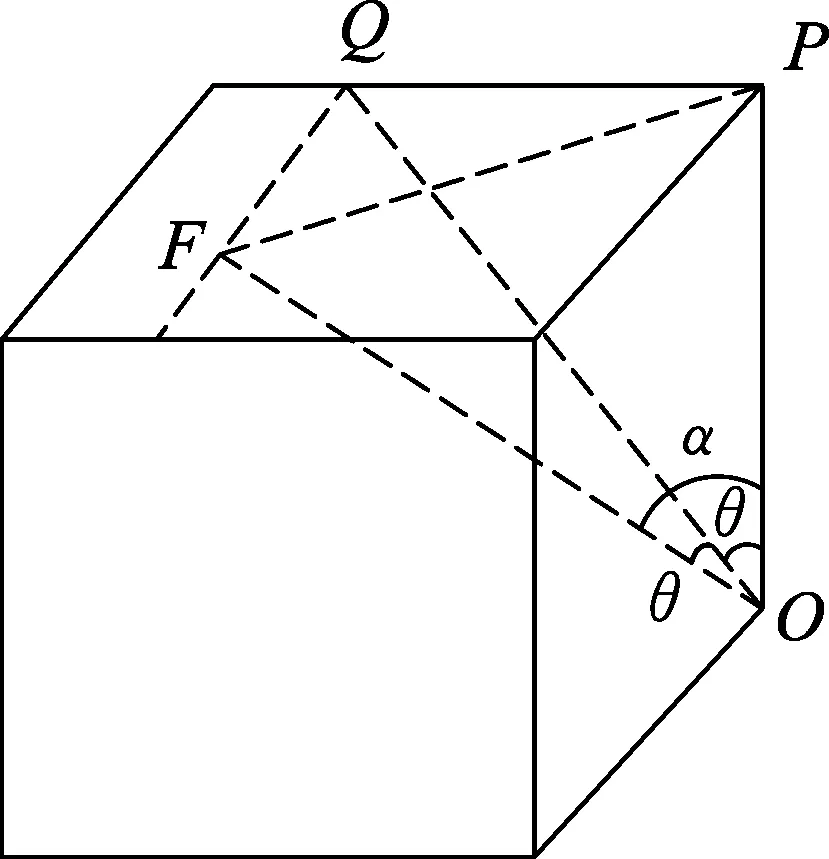
图5

如图5所示,设平面1的法向量是OP=1(单位长度),第一次将平面1转到θ角到平面2时法向量变为OQ,第二次将平面2转到θ角到平面3时法向量变为OF．OF与OP的夹角即为平面3的倾角α.由几何关系可得

PQ=tanθ,OQ=1/cosθ,QF=OQtanθ=tanθ/cosθ.

OF=1+tan2θ.

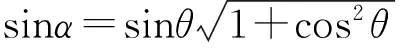
于是

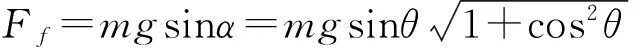
解法3:面积投影法.本问题的核心是要求转两次后的正方形所在的平面与水平面之间的夹角，可以用面积投影的方法来求此夹角．

设正方形边长为l．正方形第2次绕ab向上转θ角到平面3上时,正方形在平面2上的投影面积为S1=l2cosθ,此投影面积S1在初始平面1上的投影面积为

S=S1cosθ=l2cos2θ.

设平面3与水平面1夹角为α,应有

S=l2cosα.

可以解得

cosα=cos2θ.

于是

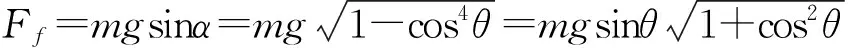
解法4:转换法.可以先不求滑块受到的摩擦力,而是求滑块受到的支持力．

滑块在平面1上时,受到斜面的支持力是N1=mg,此支持力和平面1垂直．

图6

滑块绕ad向上转θ角到平面2上时,滑块受到的支持力是N2=N1cosθ,此支持力和平面2垂直．

滑块再由平面2上绕ab向上转θ角转到平面3上时,滑块受到的支持力是N3=N2cosθ．

由以上3式可以解得N3=mgcos2θ,同样此支持力和平面3垂直．

如图6所示,设平面3与水平面1夹角为α,分析可知，N32+Ff2=(mg)2,可以解得

解法5:等效重力法.滑块在斜面上时,可以把重力分解为下滑力和紧压斜面的力,紧压斜面的力和斜面垂直,可以看成“等效重力”.

滑块在平面2上时,受到静摩擦力f1=mgsinθ,此摩擦力沿着ab方向．可以认为滑块还受到一个与平面2垂直的“等效重力”G′=mgcosθ的作用,滑块在平面2上绕ab转θ角转到平面3上时,这个“等效重力”产生的静摩擦力f2=G′sinθ=mgcosθsinθ,此摩擦力沿着bc方向,第2次转动对第一个摩擦力f1没有影响,而且最后两个分摩擦力相互垂直,于是最后的摩擦力应为

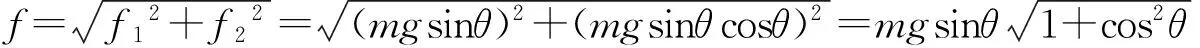
小结:做物理题目不能想当然,复杂的空间几何问题可以用数学方法来处理,数学工具的应用例如解法1中矢量分析法和解法2中的法向量旋转法来处理旋转两次后斜面的倾角问题是比较方便的,也是非常严谨的．但我们也不能忽视物理方法的应用,例如解法4中的转换法和解法5中的等效重力法．有时用物理方法来处理物理问题也会相当简洁,可以大大简化代数运算．

1 李冬冬，吴樵夫.一道静摩擦力问题的错解分析[J].物理教师，2013(12)：89.

2016-12-14)